Structural Analysis and Design Report: Cantilevers, Frames, Columns

This report presents a comprehensive structural analysis and design, covering various structural elements and systems. It begins with the calculation of bending moments (BMs) and shear forces (SFs) for cantilevers and supported beams, followed by an analysis of a 3-pin frame. The report then explores the calculation of slope and deflection of a simply supported beam using the Moment-Area Method, including a discussion of its assumptions and limitations. Finally, it addresses the determination of maximum and minimum stresses and eccentricity in short columns, detailing the axial load carrying capacity of perfectly elastic columns. The report includes detailed calculations, diagrams, and explanations, making it a valuable resource for civil engineering students. The assignment is a contribution by a student to be published on the website Desklib.

Structural Analysis and Design 1
STRUCTURAL ANALYSIS AND DESIGN
Name
Course
Professor
University
City/state
Date

Structural Analysis and Design 2
Contents
1. Task 1: Structural members and systems........................................................................................3
1.1. Task 1.1: Calculation of BMs and SFs for cantilevers and supported beams.......................3
1.2. Task 1.2: Calculation of BMs and SFs in a 3-pin frame.........................................................6
2. Task 2: Calculation of slope and deflection of simply supported beam using Moment-Area
Method.....................................................................................................................................................10
2.1. Task 2.1: Calculation of slope and deflection in simply supported beam with an overhang
10
Assumptions and limitations of area-moment method........................................................................12
3. Task 3: Maximum and minimum stresses and eccentricity of short columns.............................13
3.1. Task 3.1: Determining axial load carrying capacity of perfectly elastic columns...............13
a) Maximum and minimum stresses...............................................................................................13
b) Maximum eccentricity................................................................................................................14
References................................................................................................................................................35

Structural Analysis and Design 3
1. Task 1: Structural members and systems
1.1. Task 1.1: Calculation of BMs and SFs for cantilevers and supported beams
First, it is important to note that the bending moment (BM) at point B is zero because of the
internal hinge. At this point, the beam can rotate freely because there is no internal moment that
is generated there since bending shear is also zero.
The free body diagram (FBD) of the beam is as shown in Figure 1 below
Figure 1: FBD of the beam
Summation of forces in vertical or y direction
∑ Fy=0
RA – (5 x 3) kN – 5kN – 4kN + RD – 3kN = 0
RA + RD – 27 = 0
RA + RD = 27 kN ……………………………………………………. (1)
Summation of forces in horizontal or x direction
∑ Fx=0
HA = 0
Since the support at point A is fixed, it resists a bending moment hence there is a moment MA at
this point
Taking moments at A
∑ MA =0
-MA + (5 x 3 x 1.5) + (5 x 5) + (4 x 7) – (7RD) + (3 x 9) = 0
-MA + 22.5 + 25 + 28 – 7RD + 27 = 0
-MA – 7RD + 102.5 = 0
MA + 7RD = 102.5 kNm ………………………………………………… (2)

Structural Analysis and Design 4
e beam can be separated into two parts as shown in Figure 2 below
Figure 2: Separated sections of the beam at the hinge
Taking moments at B to the left hand side
∑ MB ( LHS ) =0
-MA + 3RA – (5 x 3 x 1.5) = 0
- MA + 3RA – 22.5 = 0
3RA – MA = 22.5 ……………………………………………………. (3)
Taking moments at B to the right hand side
∑ MB ( RHS ) =0
(5 x 2) – (4RD) + (4 x 4) + (3 x 6) = 0
10 – 4RD + 16 + 18 = 0
-4RD – 44 = 0 → RD = 11 kN
Substituting the value of RD in equation 1 gives
RA + 11 = 27 kN → RA = 27 kN – 11 kN; RA = 16 kN
Therefore the support reactions are:
RA = 16 kN, RD = 11 kN and HA = 0 kN
Substituting the value of RD in equation 2 gives
MA + (7 x 11) = 102.5 kNm → MA = 102.5 kNm – 77 kNm; MA = 25.5 kNm
Substituting the value of RA in equation 3 gives
(3 x 16) – MA = 22.5 kNm → MA = 48 kNm – 22.5 kNm; MA = 25.5 kNm
Shear force diagram (SFD)
To draw the SFD of the beam, shear forces at different points of the beam have to be determined.
These shear forces are calculated as follows:

Structural Analysis and Design 5
Shear force at A
VA = 16 kN
Shear force at B
VB = 16 kN – (5 x 3) kN = 1 kN
Shear force at C
VC1 = 1 kN
VC2 = 1 kN – 5 kN = -4 kN
Shear force at D
VD1 = - 4 kN
VD2 = - 4 kN – 4 kN + 11 kN = 3 kN
Shear force at E
VE1 = 3 kN
VE2 = 3 kN – 3 kN = 0 kN
Bending moment diagram
To draw the BFD of the beam, bending moments at different points of the beam have to be
determined. These bending moments are calculated as follows:
Bending moment at A
MA = - 22.5 kNm
Bending moment at B
MB (LHS) = -25.5 + (16 x 3) – (5 x 3 x 1.5) = -25.5 + 48 – 22.5 = 0
Bending moment at C
MC (LHS) = -25.5 + (16 x 5) – (5 x 3 x 3.5) = -25.5 + 80 – 52.5 = 2 kNm
Bending moment at D
MD (LHS) = -25.5 + (16 x 7) – (5 x 3 x 5.5) – (5 x 2) = -25.5 + 112 – 82.5 – 10 = -6 kNm
Bending moment at E
ME = 0
Since there is a change of sign of the bending moment between C and D, it means that the
bending moment diagram crosses or cuts the beam at a point between C and D. This point is
determined using the method of reflection of triangles as follows:
Let the location of zero bending moment be at a distance x from point C towards D. Using the
method of reflection of triangles, the value of x is determined as:

Structural Analysis and Design 6
x
2 = 2−x
6
6x = 4 – 2x → 8x = 4; x = 0.5m
This means that the location of zero bending moment is at a distance of 0.5m from point C or
5.5m from point A.
Therefore the shear force diagram and bending moment diagram of the beam are as shown in
Figure 3 below
Figure 3: SFD and BMD of the beam
1.2. Task 1.2: Calculation of BMs and SFs in a 3-pin frame
The free body diagram (FBD) of the frame is as shown in Figure 4 below
Figure 4: FBD of the frame
Summation of forces in vertical or y direction
∑ Fy=0

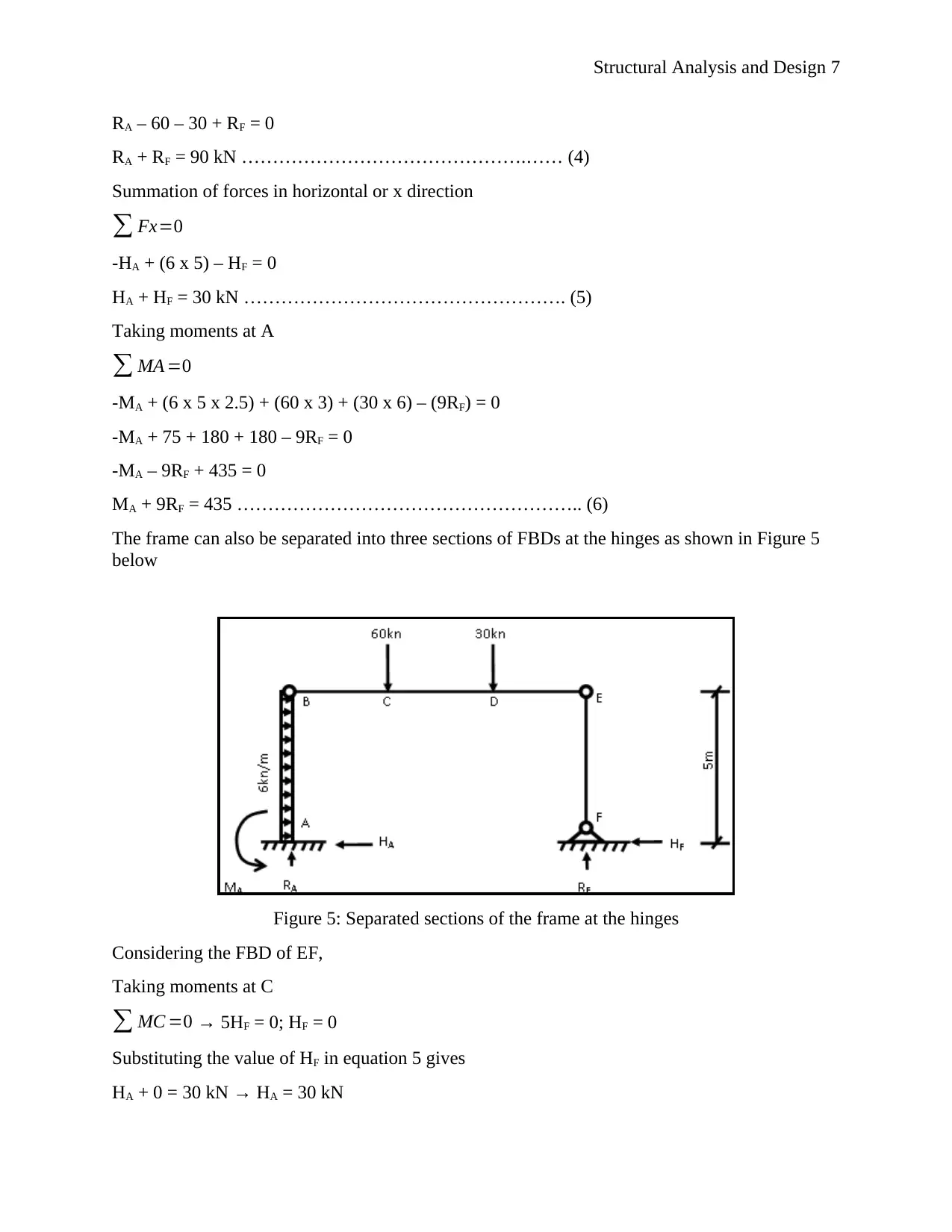
Structural Analysis and Design 7
RA – 60 – 30 + RF = 0
RA + RF = 90 kN ……………………………………….…… (4)
Summation of forces in horizontal or x direction
∑ Fx=0
-HA + (6 x 5) – HF = 0
HA + HF = 30 kN ……………………………………………. (5)
Taking moments at A
∑ MA =0
-MA + (6 x 5 x 2.5) + (60 x 3) + (30 x 6) – (9RF) = 0
-MA + 75 + 180 + 180 – 9RF = 0
-MA – 9RF + 435 = 0
MA + 9RF = 435 ……………………………………………….. (6)
The frame can also be separated into three sections of FBDs at the hinges as shown in Figure 5
below
Figure 5: Separated sections of the frame at the hinges
Considering the FBD of EF,
Taking moments at C
∑ MC =0 → 5HF = 0; HF = 0
Substituting the value of HF in equation 5 gives
HA + 0 = 30 kN → HA = 30 kN

Structural Analysis and Design 8
Considering the FBD of AB
Taking moments at B
∑ MB=0
-MA – (6 x 5 x 2.5) + 5HA = 0 → -MA – 75 + (5 x 30) = 0
MA = 75 kNm
Substituting the value of MA in equation 6 gives
75 + 9RF = 435 → RF = 40 kN
Substituting the value of RF in equation 4 gives
RA + 40 = 90 kN → RA = 50 kN
Therefore all necessary support and joint reactions and moments have already been determined.
The next step is to draw FBDs for the members and joints of the frame (Neuenhofer, 2009),
including forces of the members. These FBDs are as shown in Figure 6 below
Figure 6: FBDs for the frame’s members and joints
The axial force diagram, SFD and BMD for the three hinged frame are as shown in Figure 7, 8
and 9 below

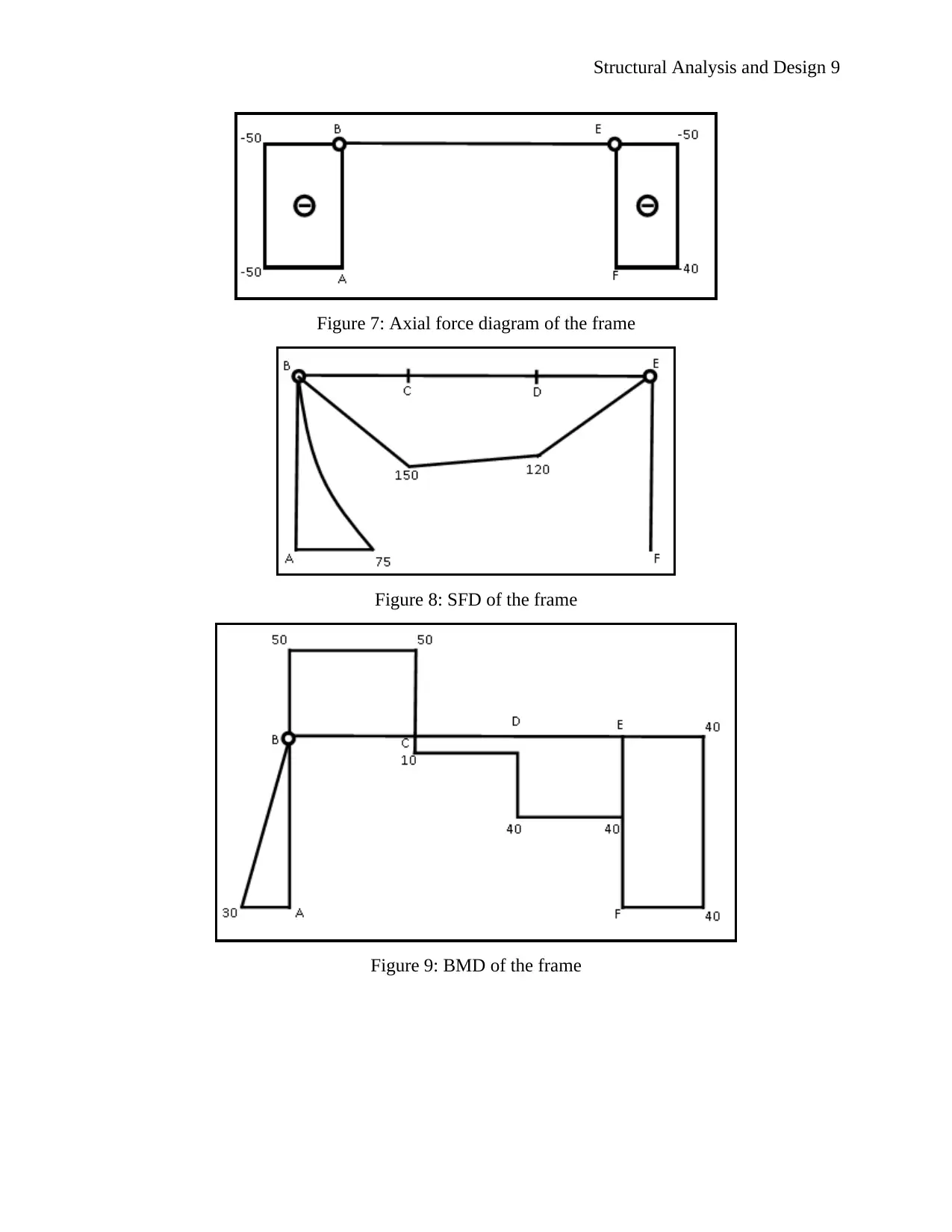
Structural Analysis and Design 9
Figure 7: Axial force diagram of the frame
Figure 8: SFD of the frame
Figure 9: BMD of the frame

Structural Analysis and Design 10
2. Task 2: Calculation of slope and deflection of simply supported beam using
Moment-Area Method
2.1. Task 2.1: Calculation of slope and deflection in simply supported beam with an
overhang
Finding reactions a supports
The free body diagram of the beam is as shown in Figure 10 below
Figure 10: FBD of the beam
Summation of forces in vertical or y direction
∑ Fy=0
RA – 10kN + RB – 5kN = 0
RA + RB = 15 kN …………………………………………………… (7)
Summation of forces in horizontal or x direction
∑ Fx=0
HA = 0
Taking moments at A
∑ MA =0
(10 x 3) – 6RB + (5 x 9) = 0
30 – 6RB + 45 = 0
6RB = 75; RB = 12.5 kN
Substituting the value of RB in equation 7 gives
RA + 12.5 kN = 15 kN
RA = 15 kN – 12.5 kN = 2.5 kN
Taking moment at a point located between A and C and which is at a distance x from point D
Mx = -10(x – 6) + RB(x – 3) – 5x
According to the moment-area method, Moment, M = EI d ² y
dx ²

Structural Analysis and Design 11
Therefore EI d ² y
dx ² =−10 ( x −6 ) + RB ( x −3 ) −5 x (substituting the value of RB = 12.5)
EI d ² y
dx ² =−10 ( x −6 ) +12.5 ( x−3 )−5 x ……………………………………….. (8)
Integrating equation 8 gives
EI dy
dx =−10 ( x−6 ) 2
2 + 12.5 ( x−3 ) 2
2 −5 x2
2 +C 1………………………………………… (9)
Integrating equation 9 gives
EI y=−10 ( x−6 ) 3
6 + 12.5 ( x−3 ) 3
6 −5 x3
6 +C 1 x +C 2……………………….……… (10)
C1 and C2 are constants and are calculated using the following boundary conditions:
When x = 3m, y = 0; and when x = L = 9m, y = 0
Substituting y = 0 when x = 3 in equation 10 gives
0=−10 (−3 )3
6 + 12.5 ( 0 )3
6 −5 ( 3 )3
6 +3 C 1+C 2
0=45+0−22.5+3 C 1+C 2
−22.5=3C 1+ C 2 ……………………………………… (11)
Substituting y = 0 when x = L = 9 in equation 10 gives
0=−10 ( 3 ) 3
6 + 12.5 ( 6 ) 3
6 −5 ( 9 )3
6 +9 C 1+C 2
0=−45+ 450−607.5+9 C 1+C 2
0=−202..5+ 9 C 1+C 2
202.5=9 C 1+C 2 ………………………………………… (12)
Equation 11 and 12 are simultaneous equations.
The equations can be solved as follows
3 C 1+C 2=−22.5→ C 2=−22.5−3 C 1
Substituting the C2 in equation 12 gives
202.5 = 9C1 + (-22.5 – 3C1)
202.5 = 6C1 – 22.5
6C1 = 225; C1 = 37.5
Hence C2 = -22.5 – 3(37.5); C2 = -135

Structural Analysis and Design 12
Substituting the value of C1 and C2 in equation 9 and 10 gives
dy
dx = 1
EI [ −10 ( x−6 )2
2 + 12.5 ( x−3 )2
2 − 5 x2
2 +37.5] …………………………………. (13)
y= 1
EI [ −10 ( x−6 ) 3
6 + 12.5 ( x−3 ) 3
6 − 5 x3
6 + 37.5 x−135 ] ……………………… (14)
Therefore equation 13 is the one used to determine slope at any point of the beam whereas
equation 14 is the one used to determine deflection of the curve at any point of the beam.
Slope at A
At A, x = L = 9 m
Therefore slope at A is determined by substituting x with 9 in equation 13 as follows
dy
dx = 1
EI [ −10 ( 9−6 )2
2 + 12.5 ( 9−3 )2
2 − 5 ( 9 )2
2 +37.5]
dy
dx = 1
EI [ −10 ( 3 ) 2
2 + 12.5 ( 6 ) 2
2 −5 ( 9 ) 2
2 +37.5]
dy
dx = 1
EI [−90
2 + 450
2 − 405
2 +37.5]
dy
dx = 1
EI [−45+225−202.5+37.5]
dy
dx = 1
EI [15]
dy
dx = 15
EI radians (where EI is in kNm2).
Deflection at D
At D, x = 0
Therefore deflection at D is determined by substituting x with 0 in equation 14 as follows
y= 1
EI [ −10 ( 0−6 )3
6 + 12.5 ( 0−3 )3
6 − 5 ( 0 )3
6 +37.5(0)−135]
y= 1
EI [ −10 (−6 ) 3
6 + 12.5 ( −3 ) 3
6 −0+0−135]
y= 1
EI [ −10 (−6 )3
6 + 12.5 (−3 )3
6 −0+0−135]
y= 1
EI [ −−2160
6 +−337.5
6 −0+ 0−135 ]

Structural Analysis and Design 13
y= 1
EI [360−56.25−0+0−135]
y= 1
EI [168.75]
y= 168.75
EI (where EI is in kNm2).
Assumptions and limitations of area-moment method
The assumptions made when using moment area method are: the beam is homogenous thus
the value of EI is constant; the beam is straight initially (before load is applied on it); the
deformations are as a result of bending; and bending causes the loads cause the beam to deform
elastically hence elastic curve’s deformation and slope are very small (Mubeen, 2011). Therefore
the limitation of moment area method is that it is not suitable for non-homogenous beams and
other beams that are deformed by other failures besides bending.
3. Task 3: Maximum and minimum stresses and eccentricity of short columns
3.1. Task 3.1: Determining axial load carrying capacity of perfectly elastic columns
a) Maximum and minimum stresses
Assuming that the edges of the column are labelled as shown below. The maximum stresses
will occur at the edges B and D because they are the ones closest to the load and therefore they
will be subjected to more stress. On the other hand, minimum stresses will occur at the edges A
and C because they are far from the load hence they will be subjected to lesser stress.
This column is symmetrical because the eccentric loading is about one axis. Since the load is
acting along the x-x axis of the column, only eccentricity from the y-y axis (ey) will apply.
The formulae for determining maximum and minimum stresses in the column section are given
in equation 15 and 16 respectively

Structural Analysis and Design 14
σ max ¿ P
A (1+ 6 e
b ) ……………………………………………………….. (15)
σ min ¿ P
A (1− 6 e
b ) ………………………………………………………… (16)
Where P = vertical compressive load acting on the column, A = cross sectional area of the
column, e = eccentricity of the load acting on the column, and b = width of the column.
Equation 15 is the summation of direct stress ( P
A ) and bending stress ( 6 Pe
Ab ) while equation 16 is
the difference between direct stress and bending stress.
Cross sectional area of the = 500 x 300 = 150,000 mm2
P = 200 x 103 N, ey = 50 mm, b = 500 mm
Direct stress, P
A = 200,000
150,000 =1.333 N /mm ²
Bending stress, 6 Pe
Ab =6 x 200,000 x 50
150,000 x 500 =0.8 N /mm ²
Since direct stress is greater than bending stress, it means that stress throughout the
column section will be compressive (that is, of the same nature). If direct stress is less than
bending stress then some section of the column will experience compressive stress while others
will experience tensile stress. And if direct stress is equal to bending stress then the entire
column section will experience the same nature of stress but minimum stress will be zero
whereas maximum stress will be twice direct stress.
Therefore,
σ max ¿ 200,000
150,000 (1+ 6 (50)
500 ) = 4
3 (1+ 3
5 ) = 4
3 ( 8
5 ) = 32
15 = 2.133 N/mm2
σ min ¿ 200,000
150,000 (1− 6(50)
500 ) = 4
3 (1−3
5 ) = 4
3 ( 2
5 ) = 8
15 = 0.533 N/mm2
b) Maximum eccentricity
Eccentricity has significant effect on the stability of both short and long columns (Bamonte
& Lo Monte, 2015). Thus it is important to determine maximum eccentricity when designing a
column (Balaji, et al., 2016). The maximum eccentricity is also known as limit of eccentricity,
denoted as elimit or emax. This is basically the maximum distance from the column’s centre within
which the load acts on the column without causing any tensile stress. Maximum eccentricity or
limit of eccentricity is determined from the minimum stress acting on the column. If the load acts
on the column within the limit of eccentricity, minimum stress will be positive (i.e.
compressive). If the load acts on the column at the point of limit of eccentricity, minimum stress
will be zero. And if the load acts on the column at a point that is beyond the limit of eccentricity,
minimum stress will be negative (i.e. tensile). In this question, the maximum eccentricity
required is when the load is acting at limit of eccentricity. This means that the minimum stress
will be zero.

Structural Analysis and Design 15
Therefore maximum eccentricity is calculated using equation 16 as follows
σ min ¿ P
A (1− 6 e
b ) (Where σmin = 0, P = 200,000 N, A = 150,000 mm2, b = 500mm)
0 ¿ 200000
150000 (1− 6 emax
500 )
0 ¿ 4
3 (1−6 emax
500 )
0 ¿ (1− 6 emax
500 )
0 = 1 – 0.012emax
0.012emax = 1
emax = 83.33 mm
Therefore, maximum eccentricity is 83.33 mm from Y-Y axis along X-X axis.
Task 4.1 Analysis and Design of Structural Steel Beam and column according to BS Code

Structural Analysis and Design 16
(a) Loadings: (Ultimate Loads)
Maximum Moment, Mx =1433 kN-m
Point Load, P =159kN
Maximum Shear at Support, Fv =220kN
Distance of point load from nearer support, ae =3000mm
Total Span, L= 6000 mm
Maximum Shear at Point Load
Load factor for Imposed Loads, γf i = 1.5
Or at Point of Maximum Moment, Fvc =0kN
(b) Characteristic Imposed Load = 5 kN/m2
Check the adequacy of the steel beams B2 and B3 with respect to bending, shear and deflection
(the beams has to support brittle finishes). The sizes of the steel beams are: B2-457 x 191 x 67
kg/m UB
2. Member Checks:
2.1 Trial Section: 457x191x67 UB Steel Grade = S 275

Structural Analysis and Design 17
From Member Capacity Tables (Blue Book)
Moment Capacity, Mc = 0.00 kN-m
2.2 Section Properties:
D = 453.4mm b =94.95mm r =10.20mm Local Buckling Ratios
B = 189.90mm d =407.60mm E = 2.05E + 05 N/mm2 b/T = 7.48
t = 8.50mm Sx = 1471cm3 Ix = 29380 cm4 d/t = 48.00
T = 12.70mm Zx = 1296 cm3 ry = 41.2 mm
X= 37.9
Local Buckling
2.3. Section classification
T<16mm
Therefore py=275Nmm2 ε =√ ¿ = √ [ 275
275 ] =1.00
For Rolled Section; Outstand Element of Compression Flange
Table 11; For Flange b/T = 9 ε = 9 x 1.0 = 9.0; Actual b/T =7.48<9.0 Flange is class 1 plastic
Web of an I-, H- or Box Section; Neutral Axis at Mid-depth
Eor web; d/t = 80 ε = 80 x 1.0 = 80.0 ; Actual d/t = 48.00 < 80.0 Web is class 1 plastic

Structural Analysis and Design 18
Therefore section is class 1 plastic
2.4 Check For Shear Buckling if : d/t > 70 ε
70 ε = 70 x 1.00 = 70.0 ; Actual d/t = 48.00 < 70.0
2.5 Check For Shear Capacity; Fv or Fvc ≤ Pv
py =275N/mm2 ; Av = t D = 8.5 x453.4 =3853.9mm2
Pv = 0.6 py Av ; Pv = 0.6 x275N/mm2 x3853.9mm2 =635894 N ≈636kN >158.8 kN
↓
Adequate for shear
2.6 Check For Moment Capacity : Mx ≤ Mcx
Check for High/Low Shear (at point of Maximum Moment, Fvm)
Shear at point of Maximum Moment; ; Fvc =0kN
Limiting Shear, Fve = 0.60x Pv = 0.60x636kN =382kN >0kN Low shear
For Low Shear (for Class 1 Plastic or Class 2 Compact cross-sections)
Mcx = py Sx 275N/mm² x1471cm³ =404.5kN-m >357.2kN-m Adequate for Flexure
2.7 Check Limit To Avoid Irreversible Deformation Under Serviceability Loads :
For simply supported beam : Mcx ≤1.2py Zx
Mcx = 1.2 x275N/mm2 x1296cm3
404.5< 427.68kN-m Adequate for flexure
2.8 Web Bearing and Buckling Under the Point Load :
2.8.1 Bearing capacity of the unstiffened web; : P ≤ Pb w ; Pb w = (b 1 + n k ) t py w;
py w =275N/mm2
b1 = t + 1.6r + 2T =50.2mm ; n = 5 (not at the end of the member) ; k = T+r =22.9mm
Pbw = [50.2+ ( 5 x22.9 ) ] 8.5 x275= 385.03kN >0 kN
; Therefore Bearing Capacity of the unstiffened web under the point load is adequate
2.8.2 Buckling resistance of the unstiffened web : P ≤ P x ;
Check if ; a e ≥ 0.7d ; a e is the distance from the load to the nearer end of the member =0 mm

Structural Analysis and Design 19
0 ≥ 0.7 x407.60 ;0 < 285.3mm
; Therefore Px= ae + 0.7 d
1.4 d x 25 ε T
√ (b 1+nk )d Pbw ; Px= 25 x 1.0 x 12.7 x 385.0
1
√ ( 50+5 x 22.9 } x 407.60
Px= 471.79KN X 0.50 x235.9KN
¿0KN
; Therefore Buckling Resistance of the unstiffened web under the point load is adequate
2.9 Web Bearing and Buckling at the Support
2.9.1 Bearing capacity of the unstiffened web : Fv ≤ Pb w ; Pb w = (b 1 + n k ) t py w;
py w=275N/mm
b1 = t + T + 0.8r – g =8.5+ 12.7+ 0.8 x10.2- 10 =19.36mm(properties of the supporting element)
n = 2 + 0.6b e /k ≤ 5 ; b e is the distance to the nearer end of the member from the end of the stiff
bearing = 0 mm
n = 2 + 0.6 x 0 /22.9 =2.0< 5 ; Therefore use n =2.0; k = T+r =12.7 +10.2 =22.9 mm
Pbw = [19.4 + (2.0 x22.9 ) ]8.5 x275 =152.3kN <158.8 kN
; Therefore Bearing Capacity of the unstiffened web at the support is NOT adequate; provide
stiffener
2.9.2 Buckling resistance of the unstiffened web : Fv ≤ P x ;
Check if ; a e ≥ 0.7d ; a e is the distance from the reaction to the nearer end of the member =25
mm
25 ≥0.7 x407.60 ;25 <285.3mm ;
Therefore Px= ae + 0.7 d
1.4 d x 25 ε T
√ (b 1+nk ) d Pbw ; Px= 25 x 1.0 x 12.7 x 153.2
1
√ ( 50+5 x 22.9 } x 407.60
Px= 296.74KN X0.54 = 161 KN
¿ 158.8KN
; Therefore Buckling Resistance of the unstiffened web at the support is adequate

Structural Analysis and Design 20
2.10 Serviceabilty Limit States : Deflection Check
The serviceability Loads are taken as unfactored imposed loads. In this case, as only ultimate
loads are the available data,the unfactored imposed loads will be taken as Mc or P / γf i
conservatively, for simplicity; γf i to be the load factor = 1.5
From Maximum Moment, Mc; wi = Unfactored Distributed Load
Mc = 1.5 Wi Le2 ; W = 8 MC
1.5 Le
2 = 8 x 357 KN −m
1.5 x 9.02 m =23.5KN/m
8
From point Load P; W, Unfactored point load
P = 1.5Wi ; Wi =
P
1.5 =
0.0
1.5 = 0 KN
The total deflection is given by:
δ = 5W i Le
4
384 EI = 5 X 23.5 X 9.04
384 X 2.E+05 X 29380 =33.361 mm ¿ 50.00 mm Adequate for deflection
Limits for calculated deflection (2.5. 2 Table 8) for: Cantilever
Allowable deflection, δa = Le
180 = 9000
180 =50.00mm
Therefore; 457x191x67 UB is adequate, Adopt Section
2.11 Lateral Torsional Buckling : Mx ≤ Mb/m LT ;
Maximum Major axis Moment in the segment; =2KN-m
Effective length of the segment LE = 700mm
λ=LE/ry =700 /41.2 =17 ; λ/x =17.0 /37.9= 0.4 ; η = 0.5 (Equal flange) ; v =1.00(Table 19)
u = 0.9 (for Rolled I of Equal flange-4.3.6.8 )
Equivalent Slenderness ; λLT = uvλ√βw

Structural Analysis and Design 21
λLT = 0.9 x1.00 x17.0x √ 1.0 = 15
β W = 1.0 (for Class 1 Plastic or Class 2 Compact Sections-4.3.6.9 )
Limiting equivalent slenderness ; λLO = 0.4(π ²E /py)0.5
λLO = 0.4 x ( π ² x2.05E+05 /275)0.5 =34.31
Perry factor & Robertson constant ; ; η LT = a LT(λLT-λLO)/1000 ; a LT = 7.0
η LT = 7.0 x (15 -34.31)/ 1000 =-0.1
p E = π ² E/ λLT2
= π ² x2.05E+05 /15 2 =8703 ; Φ LT = p y +(η<+1) p E
2 = 275+ ( −0.1+1 ) 8703
2 = 3908
Bending Strength ; Pb =
P y P y
∅¿ +(∅ ¿2−PE Py
)2 = 8703 x 275
3908+¿ ¿ =319 N/mm2
Buckling Resistance Moment; Mb = p b Sx =319 x1471000 =469.57kN-m
Uniform Moment Factor for Lateral Torsional Buckling (General case); m LT
Moments at quarter points Moments at mid-point
M2 = 2KN-m M3 = 2KN-m
M4 = 2KN-m
MLT = 0.2 + 0.15 M 2 +0.15 M3 +0.15 M4
MX = 0.2 + 0.15 x 2+0.50 x 2+0.15 x 2
2 = 1.00
Mb
m¿
= 469.57
1.00 = 470 KN-m ¿ 2 KN −m Therefore Buckling Resistance; Moment is adequate
DESIGN OF SIMPLY SUPPORTED ROLLED STEEL I or H SECTION

Structural Analysis and Design 22
(a) Check the adequacy of the steel beams B2 and B3 with respect to bending, shear and
deflection (the beams has to support brittle finishes).
B3- 457 x 191 x 67 kg/m UB
Beam No. : B-3 Gridlines : /
Limited to Plastic Section & Major Axis
Bending only)
Code / 1. Loadings : (Ultimate Loads)
Clause Maximum Moment, Mx =1433 kN-m
BS5950 Maximum Shear at Support,Fv =220 kN
Part 1 : Total Span, L =6000 mm
2000 / Load factor for Imposed Loads, γf i = 1.5
Point Load, P =159 kN
Distance of point load from nearer support, ae =3000 mm
Maximum Shear at Point Load
or at Point of Maximum Moment, Fvc =0kN
2. Member Checks :
2.1 Trial Section :457x191x67 UB Steel Grade = S 275
From Member Capacity Tables (Blue Book)
Moment Capacity, Mc= 0.00 kN-m
2.2 Section Properties
D =453.4mm b = 94.95 mm r =10.20 mm Local Buckling Ratios :
B = 189.90 mm d = 407.60 mm E =2.05E+05N/mm2 b/T = 7.48
t =8.50mm Sx = 1471 cm3 Ix =29380 cm4 d/t = 48.00
T =12.70mm Zx =1296cm3 ry =41.2 mm
x = 37.9
2.3 Section Classification

Structural Analysis and Design 23
T < 16 mm ε =√ ( 275
Py ) = √ ( 275
275 ) = 1.00
Therefore; py = 275 N/mm
2.3.1 For Rolled Section; Outstand Element of Compression Flange -
Table 11;For Flange : b/T = 9 ε = 9 x 1.0 = 9.0; Actual b/T =7.48 < 9.0Flange is Class 1 Plastic
Web of an I-, H- or Box Section; Neutral Axis at Mid-depth -
For Web :d/t =80ε = 80x 1.0 = 80.0 ;Actual d/t = 48.00 < 80.0 Web is Class 1 Plastic
Therefore : Section is Class 1 Plastic
2.4 Check For Shear Buckling if : d/t > 70 ε
70ε = 70x 1.00 = 70.0 ;Actual d/t =48.00 <70.0 No need to check for Shear Buckling
2.5 Check For Shear Capacity : Fv or Fvc ≤ Pv
py= 275N/mm2 ;Av= t D =8.5 x 453.4 = 3853.9 mm2
Pv= 0.6 py Av;Pv= 0.6 x275 N/mm2 x 3853.9 mm2 =635894N ≈ 636 kN > 220.0 kN
; Adequate for
Shear
4.2.5 2.6 Check For Moment Capacity : Mx ≤ Mcx
Check for High/Low Shear (at point of Maximum Moment, Fvm)
Shear at point of Maximum Moment ;Fvc =0kN
Limiting Shear, Fve= 0.60 x Pv=0.60 x 636kN = 382 kN> 0kN → Low Shear
For Low Shear (for Class 1 Plastic or Class 2 Compact cross-sections)
Mcx = py Sx =275 N/mm² x1471 cm³ =404.5 kN-m <1433.0 kN-m ; Fails in Flexure
2.7 Check Limit To Avoid Irreversible Deformation Under Serviceability Loads

Structural Analysis and Design 24
For simply supported beam : Mcx ≤ 1.2 py Zx
Mcx = 1.2 x 275 N/mm2 x 1296 cm3
404.5 < 427.68 kN-m ; Adequate for Flexure
2.8 Web Bearing and Buckling Under the Point Load :
2.8.1 Bearing capacity of the unstiffened web : P ≤ Pb w ;Pb w = (b 1 + n k ) t py w ; py w=
275 N/mm2
b1 = t + 1.6r + 2T= 50.2 mm; n = 5 (not at the end of the member) ; k = T+r =22.9 mm
Pbw = [ 50.2 + (5 x 22.9 ) ]8.5 x 275 = 385.03 kN > 159 kN
2.8.2 Buckling resistance of the unstiffened web : P ≤ P x ;
Check if; a e ≥ 0.7d ; a e is the distance from the load to the nearer end of the member
= 3000 mm
3000 ≥ 0.7 x407.60 ; 3000 > 285.3 mm; Therefore
Px= 25 ε T Pbw ; P x= 25 x1.0 x 12.7 x385.0
√ (b1 + nk ) d √ (50+ 5 x 22.9) x407.60
P x = 471.79 kN
¿159kN
Therefore Buckling Resistance of the unstiffened web under the point load is adequate
2.9 Web Bearing and Buckling at the Support :
2.9.1 Bearing capacity of the unstiffened web : Fv ≤ Pb w ; Pb w = (b 1 + n k ) t py w
; py w = 275 N/mm
b1 = t +T + 0.8r - g=8.5 +12.7 + 0.8 x10.2- 10 =19.36mm (properties of the supporting element)
n = 2 + 0.6b e /k≤ 5 ;b e is the distance to the nearer end of the member from the end of the stiff
bearing = 0 mm
n = 2+ 0.6 x0/ 22.9 =2.0< 5 ; Therefore use n =2.0 ; k= T+r = 12.7 +10.2 =22.9mm
Pbw = [ 19.4 + (2.0 x22.9) ]8.5 x 275 = 152.3 kN<220.0 kN
Therefore, Bearing Capacity of the unstiffened web at the support is NOT adequate;
provide stiffener
4.5.3.1 2.9.2 Buckling resistance of the unstiffened web : Fv ≤ P x ;

Structural Analysis and Design 25
Check if; a e ≥ 0.7d ; a e is the distance from the reaction to the nearer end of the member
=25mm
25 ≥ 0.7 x 407.60 ;25<285.3mm ; Therefore
Px = ae+ 0.7 d
1.4 d x 25 εT
√(b1 +n k ¿)d ¿ Pbw; P x= 25 x 1.0 x 12.7 x 152.3
√ (19.4+2 x 22.9¿) x 407.60 ¿ x 25+ 285.3
1.40 x 407.6
P x = 296.74 kN x 0.54 = 161.4kN
< 220.0 kN
Therefore, Buckling Resistance of the unstiffened web at the support is NOT adequate;
provide stiffener
2.5.2 2.10 Serviceabilty Limit States : Deflection Check
The serviceability Loads are taken as unfactored imposed loads. In this case, as only ultimate
loads are the available data,
the unfactored imposed loads will be taken as Mc or P / γf i conservatively, for simplicity; γf i
to be the load factor = 1.5
From Maximum Moment, Mc; wi = Unfactored Distributed Load
Mc = 1.5 Wi Le2 ;Wi = 8Mc = 8 x 1433 KN-m = 212.3 KN/m
Maximum Major axis Moment Effective Length of the segment, L E= 700 mm
From Point Load P; Wi = Unfactored Point Load
P = 1.5 Wi ; Wi = P
1.5 = 158.8
1.5 = 106 KN
The total deflection is given by;
5Wi Le4 + Wi Le3
δ = 384 EI + 48 EI

Structural Analysis and Design 26
5 x 212.3 x 6.04
384 x 2.E+05 x 29380 +¿ 106 x 6.03
48 x 2.E+05 x 29380
= 67.389 mm > 33.33 mm Not Adequate for Deflection
Limits for calculated deflection for : Cantilever (2.5.2 Table 8)
Allowable deflection, δa
Le = 6000
δa = 180 = 180 = 33.33 mm Therefore :457x191x67 UB is NOT Adequate, Revise Section
2.11 Lateral Torsional Buckling : Mx ≤ Mb/m LT
Maximum major axis moment in the segment Effective length of the segment
Mx = 2KN-m lE = 700mm
λ=LE/ry= 700/41.2 =17; λ/x = 17.0 / 37.9= 0.4 ; η = 0.5 (Equal flange); v = 1.00 (Table 19)
u = 0.9 (for Rolled I of Equal flange-4.3.6.8 ) ; β W =1.0 (for Class 1 Plastic or Class 2 Compact
Sections-4.3.6.9 )
Equivalent Slenderness; λLT= uvλ√βw; Limiting equivalent slenderness; λLO = 0.4(π ²E /py)0.5
λLT= 0.9 x1.00 x 17.0x √ 1.0 = 15 ;λLO = 0.4 x (π ²x 2.05E+05 /275)0.5 = 34.31
Perry factor & Robertson constant ; η LT = a LT(λLT-λLO)/1000 ;a LT =7.0
η LT = 7.0 x (15 -34.31)/ 1000 = -0.1
p E = π ² E/ λLT2 ;Φ LT = p y +( η LT +1)p E = 275+(−0.1+ 1)8703
2 =
3908
2
= π ² x 2.05E+05 /15 2 = 8703
Bending Strength,
Pb = p E p y
Φ<+(Φ<2−p E p y )0.5 = 8703 x 275
3908+ (39082−8703 x 275 ) 0.5 = 319 N/mm2
Buckling Resistance Moment; Mb = p bSx = 319 x 1471000 = 469.57 kN-m

Structural Analysis and Design 27
Uniform Moment Factor for Lateral Torsional Buckling (General case); m LT
Moments at quarter points Moments at mid point
M 2 = 2 kN-m M3 = 2KN-m
M 4 = 2 kN-m
m LT = 0.2 + 0.15 M 2 +0.5 M3 +0.15 M 4
Mx = 0.2 + 0.15 x 2+0.50 x 2+0.15 x 2
2 = 1.00
Mb = 469.57 = 470 kN-m > 2kN-m Therefore, Buckling Resistance
MLT = 1.00 Moment is Adequate
Task 4.2 P4.2 Analysis and Design of Single Reinforced and simply supported rectangular
concrete beam, and short reinforced concrete column according to BS Code.
Design code: BS8110 – 1997
Reinforce Concrete Beam
Loading
D.L = 20 kN/m
I.L = 25 kN/m
Self-Weight= 0.24 ×0.4×0.7 =0.07kN/m
USL design
(20+0.07)1.4+25×1.6=60
M=(wl^2)/8 =(60.10×9.5^2)/8 =678kNm
V=F/2 = (60.10×9.5)/2 =285.48kN
Flexural capacity and reinforcement calculations:
Maximum tensile stress in
steel
fy
fst =

Structural Analysis and Design 28
1.05
460
= 1.05
= 438.095 MPa
Maximum compression stress in steel
fy
fst = 1.05
460
= 1.05
= 438.095 MPa
Equivalent rectangular stress block parameters:
ß = 0.9
 = 0.67 = 0.67
Calculation of the maximum steel strain:st = fst
Es
438.1
= 200000
= 0.0022
Balanced neutral axis
d
xb = st1 + c
670
= .00219
1 + .0035
= 412.127 mmb = 1 - %redis
100

Structural Analysis and Design 29
10
= 1 - 100
= 0.9000
Maximum allowed neutral axis depth:
x = min(d/(1+st/c) , (b-0.4)*d) = 335.000 mm
Depth of rectangular stress block:
a = . x
= .9 ×335
= 301.500 mm
Concrete moment capacity:
Mu = a. d - a . b.  . . fcu. 1×10-6
2
301.5
= 301.5 × 670 - ×400 ×.66667 ×.66667 ×35 ×1×10-6
2
= 974.123 kNm
Lever arm
z = d. 0.5 + 0.25 - M
2 .  .  . b. d2 . fcu
6780×105
= 670 × 0.5 + 0.25 -
2 ×.66667 ×.66667 ×400 ×670 2 ×35
= 575.299 mm
Tension steel
M
Ast = fst. z
6780×105
=
438.1 ×575.3
= 2 690.061 mm²
Neutral axis depth

Structural Analysis and Design 30
2 . (d - z)
Neutralaxis= 
2 ×(670 - 575.3 )
= .9
= 210.444 mm
Minimum Flexural Reinforcement
if fy<=300 fac = 1.82 else fac = 1.00
for flanged beam if bw/bf<0.4 then Minfac = 0.0018 else Minfac = 0.0013 ;Minfac = 0.0013
Amin = Minfac. bw. h. fac
= .0013 ×400 ×700 ×1
= 364.000
Shear Calculations:
Area used for shear calculations:
Ash = bw. de
= 400 ×670
= 268.0×103 mm²
Reinforcement ratio
Ast
F1 = Ash
2 690.1
= 268000
= 0.0100
f1 = f1i. 100
= .01004 ×100
= 1.004
F1 = min(3 , F1) = 1.004
F1 = max(0.15 , F1) = 1.004
f2 = 1
0.79

Structural Analysis and Design 31
vc = . F10.33333 . F20.25
1.25
0.79
= ×1.0038 0.33333 ×1 0.25
1.25
= 0.6328 MPa
fcu 0.33333
F3 = 25
35 0.33333
= 25
= 1.119
vc = vc1. F3
= .63279 ×1.1187
= 0.7079 MPa
Maximum allowable shear stress
vcu = 0.8 . fcu
= 0.8 × 35
= 4.733 MPa
vcu = min(5 , vcu) = 4.733
Actual Shear stress:
V . 1×103
v = Ash
285.48 ×1×103
= 268000
= 1.065 MPa
Shear force capacity
Vco = vc. Ash. 1×10-3
= .7079 ×268000 ×1×10-3
= 189.717 kN
Shear reinforcement

Structural Analysis and Design 32
(v - vc). b
Asv/sv = 0.95 . fyv
(1.0652 - .7079 )×400
= 0.95 ×250
= 0.6018
Minimum links
0.40 . b
Asv/svn =
0.95 . fyv
0.40 ×400
= 0.95 ×250
= 0.6737
Task 4.3 Analysis and design of axially load timber column according to BS Code.
C 18 75mm * 150m long-term- 12KN
Medium- 20KN
Calculation
Table 6 C18
Δ1911=7.1 N/mm2
K7 and k8 don’t apply

Structural Analysis and Design 33
Table 17 Long-term -k3-0
Medium k3-1.25
Clause2.11.3 Slenderness
Table 21 x-x axis lexx = (0.85*3600) = 3060
lexx
h = 3060
150 =20.4<52
y-y axis leyy ≥ 1.0 *1600= 1600 critical
or ≥ 0.85*1600=1360
lexx
b = 1800
75 =24<52
Critical slenderness=21.4
clause 12.11.5 Long-term
table 22 F/δc,11 is determined using the form Emm and Δc11= Δ,c9 11*kd
Emm=6000N/mm2
Δc11=7.1 * 11.0 =7.1N/mm2
E
δc 11 =6000
7.1 =845∧γ=24
Table 19 K12=0.43
Δc 11= δc,9 11* k0 * k12
=7.1 * 1.0 *0.4 =3.05N/mm2
Δc,9 11 = F
A
Clause 2.11.4
Clause 2.11.4

Structural Analysis and Design 34
9.0∗103
150∗75 =0.8 N
mm2 <3.05
Mid-term
Δc,11=7.1*1.25=8.8 N/mm2
E
Δ c , 911 = 6000
8.88 =675.7
Table 19 K12= 0.363
Δc=Δc,9 11 * k3 * k12
=7.1 *1.25 * 0.363 =3.22 N/mm2
Δc,9 1= F
A = 26∗103
180∗75 =2.3<322
Section ok
Task 4.4 Analysis and design of axially loaded brick column according to BS Code
Loading
Characteristic:
Roof D.L= 10
2 ∗4=20.00 KN /m
I.L = 10
2 ∗4=7.50 KN / m
Floors D.L= 10
2 ∗5∗4=50.00 KN /m
I.L= 10
2 ∗1.5∗4=30.00 KN /m
Design Load
Roofing = 20 × 1.4 + 7.5 × 1.6= 40KN/m
Column = 40∗2∗3
2 =120 KN
Floor= 50.0 × 1.4 +30 ×1.6= 118.00KN/m

Structural Analysis and Design 35
118.00∗3+3
2 =354 KN
Plaster both sides(characteristic)
2 × 0.012 × 21 × 17.2 = 6.77KN/m
102.5 Brick wall
0.1025 × 18 × 11.2 = 20.66KN/m
215 Brick wall
0.215 × 18 × 4.5 = 17.42KN/m
1.4Gx + 1.6qx
1.4 × 164.75 + 1.6 × 67.50 = 338.65 KN/m
338.65∗3+3
2 =1015.95 N
Calculations
Clause 28.22 βɧtʄk
γm
Slenderness ratio heʄ
teʄ
heʄ = 4.5 - 0.5 = 4.0
SR= 4
0.44 =9.1
Table 7 Inter polotio β = 0.985
γm =2.5
clause 19.12 A = 0.44 × 0.552 =0.24 >0.2m2
No m.f applied
βɧtʄk
γm ≥ 1015.95 KN
ʄ ≥ 1015.95∗103∗2.5
440∗552∗0.985 =10.62N/m2

Structural Analysis and Design 36
therefore ʄk required is 10.62N/m2 or mark
ʄk to use is 11.6N/m2
Material Selection
Brick with compressor strength 50N/m2 set with mortar designation (I)
References
Balaji, A., Luquman, M., Nagarajan, P. & Pillai, T., 2016. Studies on the behavior of reinforced
concrete short column subjected to fire. Alexandria Engineering Journal, 55(1), pp. 475-486.
Bamonte, P. & Lo Monte, F., 2015. Reinforced concrete columns exposed to standard fire:
comparison among different constitutive models for concrete at high temperature. Fire Safety
Journal, Volume 71, pp. 310-323.
Mubeen, A., 2011. Mechanics of solids. 2nd ed. New Delhi: Pearson India.
Neuenhofer, A., 2009. Structural analysis. San Luis Obispo: California Polytechnic State
University.