Detailed Structural Design and Analysis of Slabs, Beams, and Columns
VerifiedAdded on 2021/04/21
|41
|1318
|457
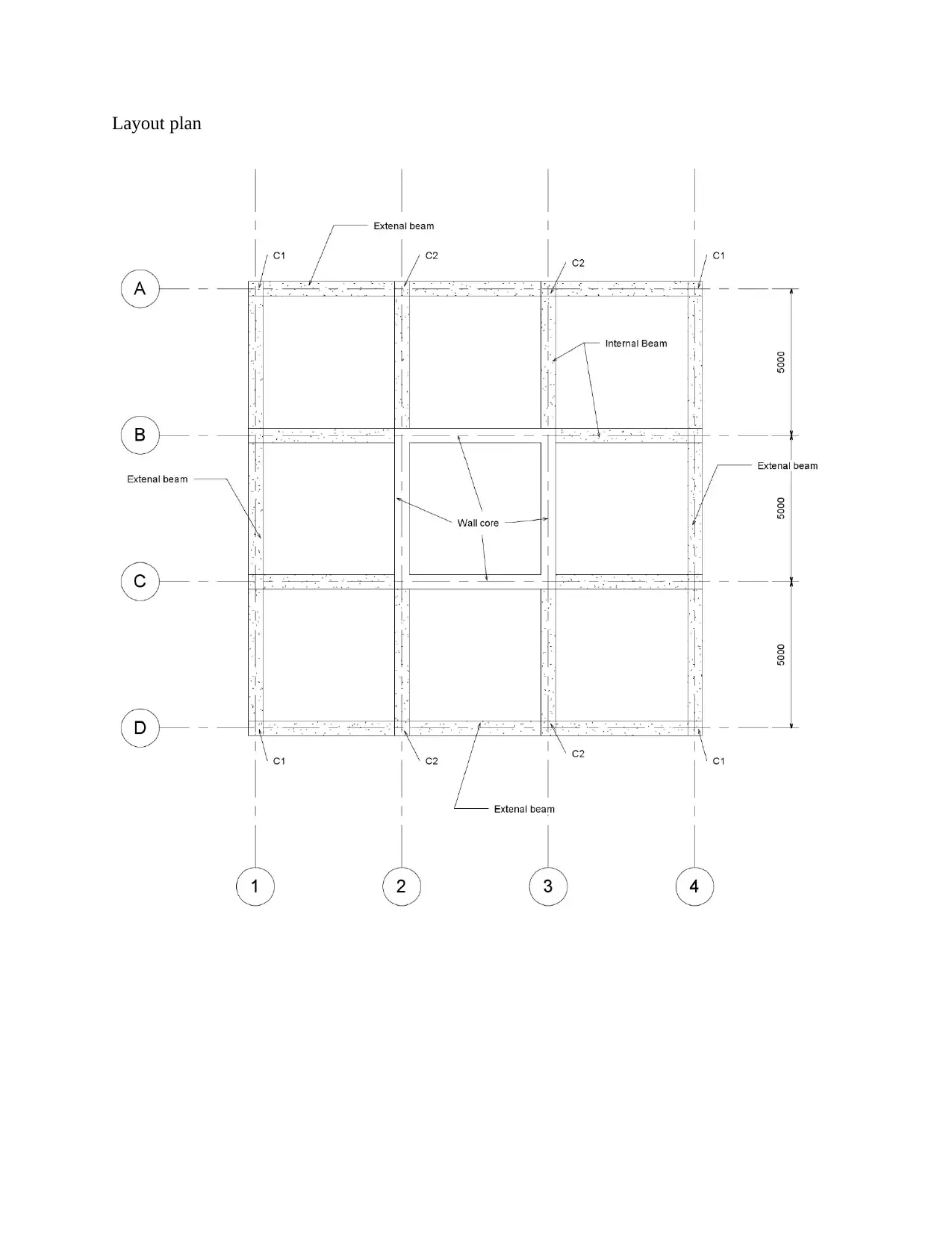
Practical Assignment
AI Summary
This document presents a comprehensive structural design analysis, covering the design of slab panels, beams, and columns. The slab design includes calculations for both corner and edged slabs, detailing load combinations, effective depths, bending moments, and reinforcement requirements for both top and bottom steel, as well as shear checks. Beam design focuses on continuous and simply supported beams, incorporating deflection checks, bending moment calculations, shear force analysis, and the determination of required reinforcement. The column design involves the analysis of axial compression, bending capacity, and the construction of an interaction diagram to assess the structural behavior under combined loading conditions. The analysis adheres to relevant Australian Standards (AS 3600) and includes detailed calculations for various load cases, ensuring structural integrity and compliance with design codes. The document provides a thorough examination of each structural element, offering insights into the design process and essential considerations for civil engineering applications.
1 out of 41
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)