SUSS MTH219e: Fundamentals of Statistics and Probability TMA Solution
VerifiedAdded on 2022/08/11
|10
|1615
|24
Homework Assignment
AI Summary
This document presents a comprehensive solution to the MTH219e Fundamentals of Statistics and Probability Tutor-Marked Assignment. The solution covers various statistical concepts including conditional probability, binomial and Poisson distributions, and geometric distribution. It includes detailed calculations and interpretations for each question, such as calculating probabilities related to ratings, defects in production lines, and mining decisions based on gamma ray readings. The assignment also explores descriptive statistics, including mean, median, standard deviation, variance, and percentiles, along with their implications on data interpretation. Furthermore, the solution demonstrates the application of these statistical methods in different scenarios, providing a thorough understanding of the subject matter. The document is a valuable resource for students seeking to understand and solve similar problems in statistics and probability.

MTH219 Fundamentals of Statistics and Probability
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Answer to question 1:
1[a]
Here, total number of rating = 400
Therefore, top 15% = 400*15% = 60
As per given information, 12 rating has been chosen from these 60 rating.
[i] Therefore, the probability that the chosen rating will be the highest rating = 12C1 / 60C1
= 12/60 = 1/5
[ii] Therefore, the probability that the chosen rating will be the lowest rating = 12C1 / 60C1
= 12/60 = 1/5
1[b]
Here, the probability of Type A = 0.03
Probability of Type B = 0.02
And probability of both Type A and Type B = 0.004
Hence, Probability of Type B given Type A is occurred = 0.004/0.03 = 0.13333
1[c]
Greater Than 70 Less than 70 Total
Dolomit
e 55 425 480
Shale 255 15 270
310 440 750
If we define A as the event that Dolomite is there and B is the even as the Gamma ray reading
is more than 70 API units, then
P(A) = 480/750 = 0.64
P(Ac) = 270/750 = 0.36
P(B/A) = 55/480 = 0.11458
P(B/Ac)=255/270 = 0.94444
1[a]
Here, total number of rating = 400
Therefore, top 15% = 400*15% = 60
As per given information, 12 rating has been chosen from these 60 rating.
[i] Therefore, the probability that the chosen rating will be the highest rating = 12C1 / 60C1
= 12/60 = 1/5
[ii] Therefore, the probability that the chosen rating will be the lowest rating = 12C1 / 60C1
= 12/60 = 1/5
1[b]
Here, the probability of Type A = 0.03
Probability of Type B = 0.02
And probability of both Type A and Type B = 0.004
Hence, Probability of Type B given Type A is occurred = 0.004/0.03 = 0.13333
1[c]
Greater Than 70 Less than 70 Total
Dolomit
e 55 425 480
Shale 255 15 270
310 440 750
If we define A as the event that Dolomite is there and B is the even as the Gamma ray reading
is more than 70 API units, then
P(A) = 480/750 = 0.64
P(Ac) = 270/750 = 0.36
P(B/A) = 55/480 = 0.11458
P(B/Ac)=255/270 = 0.94444

Therefore, P(A/B) =
P ( B
A )∗P ( A )
P ( B
A )∗P ( A ) + P ( B
Ac )∗P ( Ac )
=0.11458*0.64/(0.11458*0.64+0.9444*0.36)
= 0.177419355
Since, the probability is 17.74%, they should mine.
1[d]
Here, λ = 1/8
Since, the event is following exponential distribution, it can be said that
P(X>11)
= 1-P(X<=11)
= 1 – (1/8)*e^(-(1/8))*11
= 0.031604949
1[e]
Here, probability = 1/1000 = 0.001.
[i] it will follow binomial distribution. Hence,
= P(X<4)
=P(X =0) + P(X=1) + P(X=2) + P(X=3)
= 5000!/(0!*(5000-0)!)*p^(0)*(1-p)^(5000-0) + 5000!/(1!*(5000-1)!)*p^(1)*(1-p)^(5000-1)
+ 5000!/(2!*(5000-2)!)*p^(2)*(1-p)^(5000-2) + 5000!/(3!*(5000-3)!)*p^(3)*(1-p)^(5000-3)
= 0.264885
[ii] It will follow Poisson distribution
Hence, λ =(1/1000)*5000 = 5.
So, = P(X<4)
=P(X =0) + P(X=1) + P(X=2) + P(X=3)
P ( B
A )∗P ( A )
P ( B
A )∗P ( A ) + P ( B
Ac )∗P ( Ac )
=0.11458*0.64/(0.11458*0.64+0.9444*0.36)
= 0.177419355
Since, the probability is 17.74%, they should mine.
1[d]
Here, λ = 1/8
Since, the event is following exponential distribution, it can be said that
P(X>11)
= 1-P(X<=11)
= 1 – (1/8)*e^(-(1/8))*11
= 0.031604949
1[e]
Here, probability = 1/1000 = 0.001.
[i] it will follow binomial distribution. Hence,
= P(X<4)
=P(X =0) + P(X=1) + P(X=2) + P(X=3)
= 5000!/(0!*(5000-0)!)*p^(0)*(1-p)^(5000-0) + 5000!/(1!*(5000-1)!)*p^(1)*(1-p)^(5000-1)
+ 5000!/(2!*(5000-2)!)*p^(2)*(1-p)^(5000-2) + 5000!/(3!*(5000-3)!)*p^(3)*(1-p)^(5000-3)
= 0.264885
[ii] It will follow Poisson distribution
Hence, λ =(1/1000)*5000 = 5.
So, = P(X<4)
=P(X =0) + P(X=1) + P(X=2) + P(X=3)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

= e^(- λ)*( λ^0)/0! + e^(- λ)*( λ^1)/1! + e^(- λ)*( λ^2)/2! + e^(- λ)*( λ^3)/3!
= 0.0628875
[iii] Clearly it indicates that in case of whether there will bubble in the glass or not, the
binomial distribution is showing 26.49% probability, when the Poisson distribution is
indicating 6.29% probability.
Answer to question 2:
2[a]
[i]
Mean =(22+23+18+22+20+24+22+22+21+19+21+21+25+ 21+ 20+19+17+23+20)/20
=421/20
=21.05
The numbers can be arranged as 17, 18, 19, 19, 20, 20, 20, 21, 21, 21, 21, 21, 22, 22, 22, 22,
23, 23, 24, 25
Hence, median = (21+21)/2 = 21
Standard Deviation = √¿
==1.90984
Variance = 1.90984^2
=3.6475
Range = 25 – 17
= 8
First quartile =(n+1)/4th item
=(20+1)/4th item
=5th item+(1/4)*(6th-5th item)
=20+(1/4)*(20-20)
=20
= 0.0628875
[iii] Clearly it indicates that in case of whether there will bubble in the glass or not, the
binomial distribution is showing 26.49% probability, when the Poisson distribution is
indicating 6.29% probability.
Answer to question 2:
2[a]
[i]
Mean =(22+23+18+22+20+24+22+22+21+19+21+21+25+ 21+ 20+19+17+23+20)/20
=421/20
=21.05
The numbers can be arranged as 17, 18, 19, 19, 20, 20, 20, 21, 21, 21, 21, 21, 22, 22, 22, 22,
23, 23, 24, 25
Hence, median = (21+21)/2 = 21
Standard Deviation = √¿
==1.90984
Variance = 1.90984^2
=3.6475
Range = 25 – 17
= 8
First quartile =(n+1)/4th item
=(20+1)/4th item
=5th item+(1/4)*(6th-5th item)
=20+(1/4)*(20-20)
=20
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Third quartile=3(n+1)/4th item
=3(20+1)/4th item
=15th item + (3/4)*(16th – 15th item)
=22 + (3/4)*(22-22)
=22
IQR = Third quartile – First quartile
=22-20
=2
Coefficient of Variation = Standard Deviation / Mean
=1.90984/21.05
=0.09073
90th Percentile = 90(n)/100th value
=90*20/100th value
=18th value
=23
[ii]
Stem Leaf
1 7 8 9 9
2 0 0 0 1 1 1 1 1 2 2 2 2 3 3 4 5
2[b]
In case numbers are increased by 100, mean, median and mode will increase by 100.
However, range will remain same. The variance will be greater than the previous instance and
the skewness will remain same.
Answer to question 3:
=3(20+1)/4th item
=15th item + (3/4)*(16th – 15th item)
=22 + (3/4)*(22-22)
=22
IQR = Third quartile – First quartile
=22-20
=2
Coefficient of Variation = Standard Deviation / Mean
=1.90984/21.05
=0.09073
90th Percentile = 90(n)/100th value
=90*20/100th value
=18th value
=23
[ii]
Stem Leaf
1 7 8 9 9
2 0 0 0 1 1 1 1 1 2 2 2 2 3 3 4 5
2[b]
In case numbers are increased by 100, mean, median and mode will increase by 100.
However, range will remain same. The variance will be greater than the previous instance and
the skewness will remain same.
Answer to question 3:

3[a]
[i] Since the event is following uniform distribution, average fill per bottle =
(185+230)/2 = 207.5 ml
[ii] = P(x>210)
=1- (210-185) *1/ (230-185)
= 1-0.5556
= 0.444
3[b]
[i] p = 0.85
Hence, P(X=0)
= 6!/(0!*(6-0)!)*p^(0)*(1-p)^(6-0)
=(1-0.85)^6
=0.0000114
[ii] P(X>2) = 1-P(X=0)-P(X=1)-P(X=2)
=1-0.0000114-6! / (1! *(6-1)!) *p^ (1) *(1-p) ^ (6-1)- 6! / (2! *(6-2)!) *p^ (2) *(1-p) ^ (6-2)
=1-0.0000114-0.000387-0.005486
=0.9941156
[iii] the aim is to find 2 rats will not be favourable. It means 4 will be favourable.
P(X=4) = 6! / (4! *(6-4)!) *p^ (4) *(1-p) ^ (6-4)
=0.176177109
[iv] The mean of binomial distribution is n*p, where n = 6
Hence, Mean = 6*0.85 = 5.1
3[c]
Here, total probability = 1
Or, 0.02*(5−x) +0.002*(25−x) + 0.0005*(100−x) + 0.9775*(−x) = 1, where x is the price
[i] Since the event is following uniform distribution, average fill per bottle =
(185+230)/2 = 207.5 ml
[ii] = P(x>210)
=1- (210-185) *1/ (230-185)
= 1-0.5556
= 0.444
3[b]
[i] p = 0.85
Hence, P(X=0)
= 6!/(0!*(6-0)!)*p^(0)*(1-p)^(6-0)
=(1-0.85)^6
=0.0000114
[ii] P(X>2) = 1-P(X=0)-P(X=1)-P(X=2)
=1-0.0000114-6! / (1! *(6-1)!) *p^ (1) *(1-p) ^ (6-1)- 6! / (2! *(6-2)!) *p^ (2) *(1-p) ^ (6-2)
=1-0.0000114-0.000387-0.005486
=0.9941156
[iii] the aim is to find 2 rats will not be favourable. It means 4 will be favourable.
P(X=4) = 6! / (4! *(6-4)!) *p^ (4) *(1-p) ^ (6-4)
=0.176177109
[iv] The mean of binomial distribution is n*p, where n = 6
Hence, Mean = 6*0.85 = 5.1
3[c]
Here, total probability = 1
Or, 0.02*(5−x) +0.002*(25−x) + 0.0005*(100−x) + 0.9775*(−x) = 1, where x is the price
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
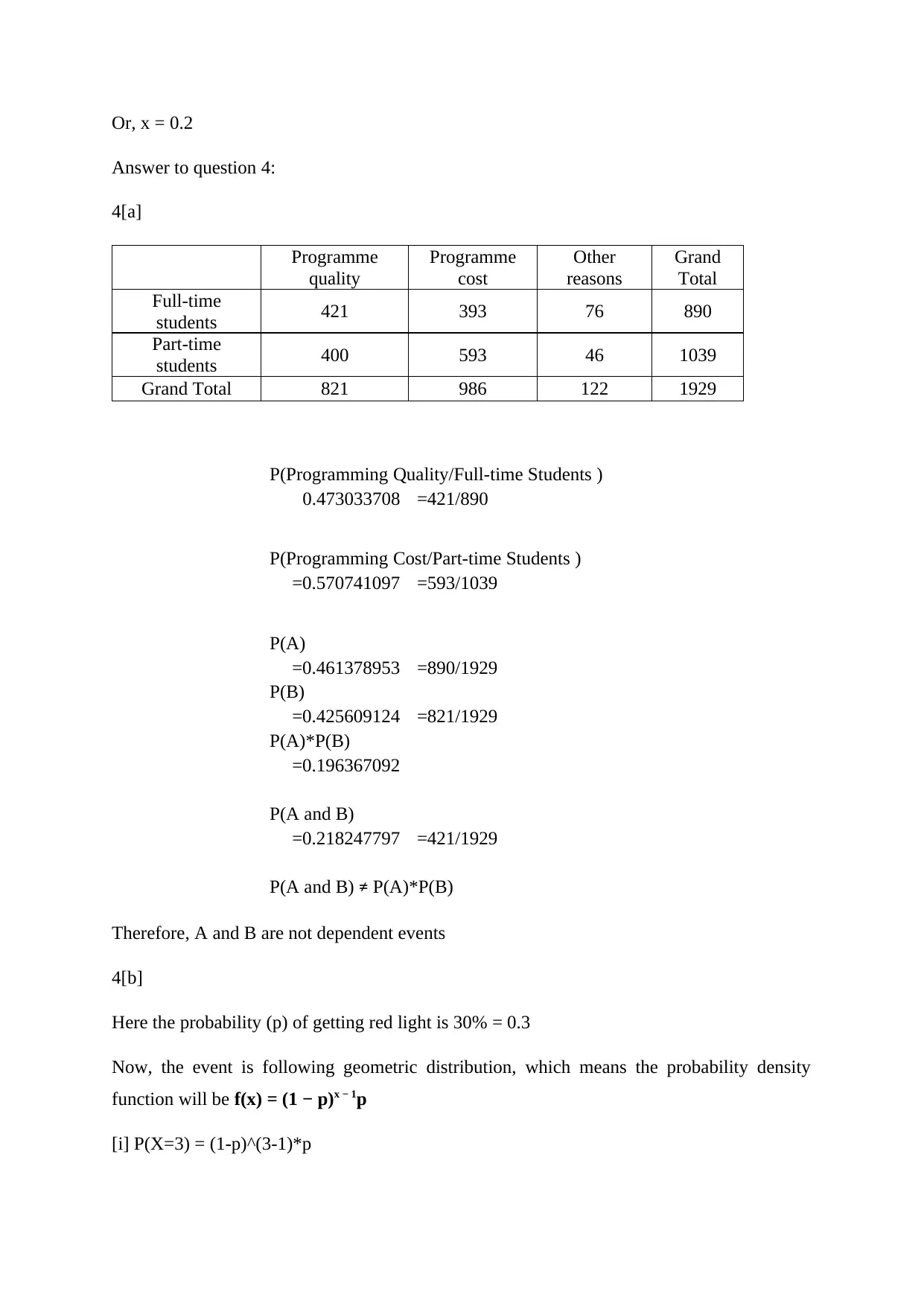
Or, x = 0.2
Answer to question 4:
4[a]
Programme
quality
Programme
cost
Other
reasons
Grand
Total
Full-time
students 421 393 76 890
Part-time
students 400 593 46 1039
Grand Total 821 986 122 1929
P(Programming Quality/Full-time Students )
0.473033708 =421/890
P(Programming Cost/Part-time Students )
=0.570741097 =593/1039
P(A)
=0.461378953 =890/1929
P(B)
=0.425609124 =821/1929
P(A)*P(B)
=0.196367092
P(A and B)
=0.218247797 =421/1929
P(A and B) ≠ P(A)*P(B)
Therefore, A and B are not dependent events
4[b]
Here the probability (p) of getting red light is 30% = 0.3
Now, the event is following geometric distribution, which means the probability density
function will be f(x) = (1 − p)x − 1p
[i] P(X=3) = (1-p)^(3-1)*p
Answer to question 4:
4[a]
Programme
quality
Programme
cost
Other
reasons
Grand
Total
Full-time
students 421 393 76 890
Part-time
students 400 593 46 1039
Grand Total 821 986 122 1929
P(Programming Quality/Full-time Students )
0.473033708 =421/890
P(Programming Cost/Part-time Students )
=0.570741097 =593/1039
P(A)
=0.461378953 =890/1929
P(B)
=0.425609124 =821/1929
P(A)*P(B)
=0.196367092
P(A and B)
=0.218247797 =421/1929
P(A and B) ≠ P(A)*P(B)
Therefore, A and B are not dependent events
4[b]
Here the probability (p) of getting red light is 30% = 0.3
Now, the event is following geometric distribution, which means the probability density
function will be f(x) = (1 − p)x − 1p
[i] P(X=3) = (1-p)^(3-1)*p
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

=(1-0.3)^(2)*0.3
=0.147
[ii]
P(X<=4) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
=(1-p)^0*p + (1-p)^1*p + (1-p)^2*p + (1-p)^3*p
=1*0.3 + 0.7*0.3+0.7*.07*.03+0.7*0.7*0.7*0.3
=0.61437
Answer to question 5:
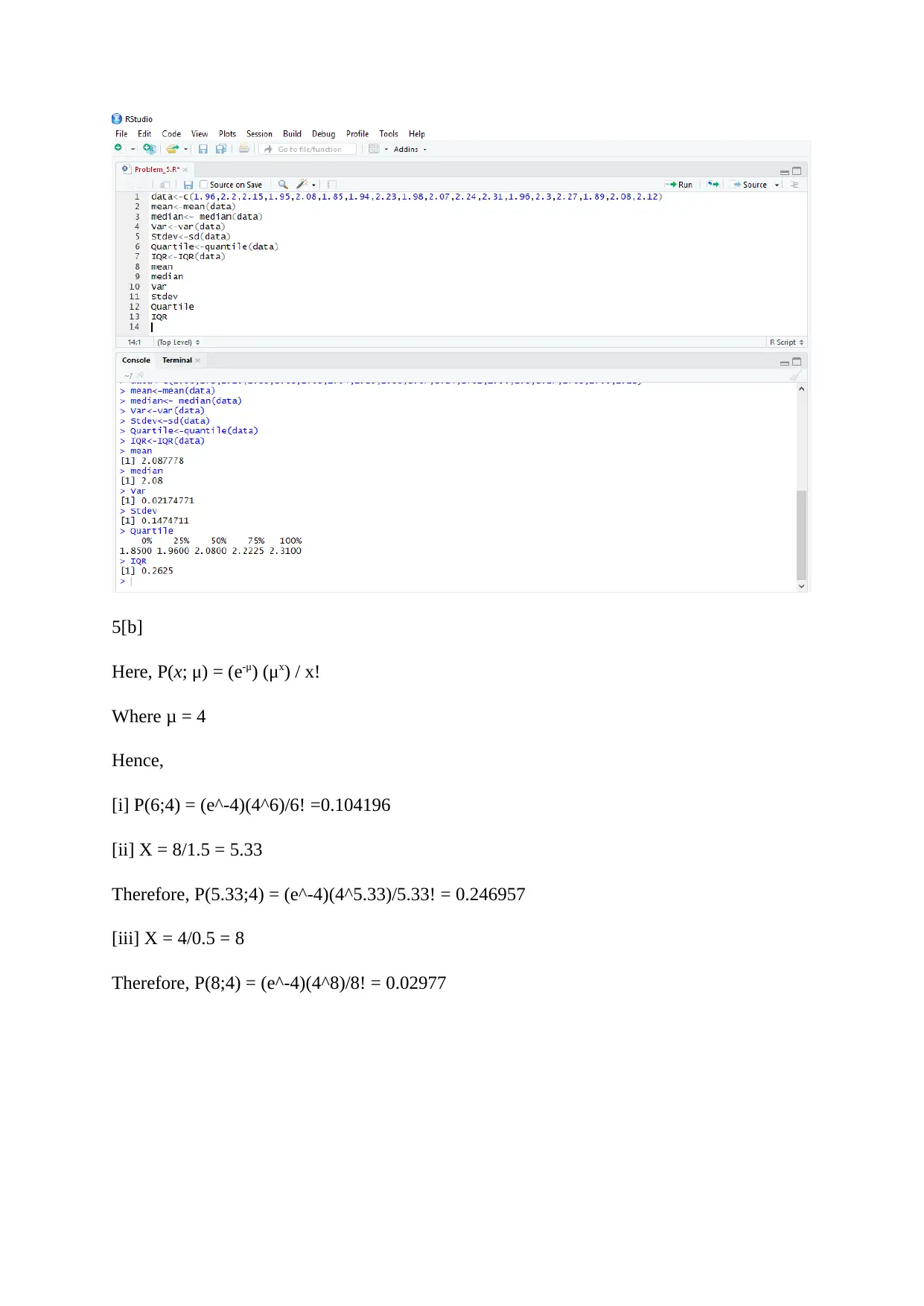
5[a]
[i]
[ii]
=0.147
[ii]
P(X<=4) = P(X=1) + P(X=2) + P(X=3) + P(X=4)
=(1-p)^0*p + (1-p)^1*p + (1-p)^2*p + (1-p)^3*p
=1*0.3 + 0.7*0.3+0.7*.07*.03+0.7*0.7*0.7*0.3
=0.61437
Answer to question 5:
5[a]
[i]
[ii]
5[b]
Here, P(x; μ) = (e-μ) (μx) / x!
Where μ = 4
Hence,
[i] P(6;4) = (e^-4)(4^6)/6! =0.104196
[ii] X = 8/1.5 = 5.33
Therefore, P(5.33;4) = (e^-4)(4^5.33)/5.33! = 0.246957
[iii] X = 4/0.5 = 8
Therefore, P(8;4) = (e^-4)(4^8)/8! = 0.02977
Here, P(x; μ) = (e-μ) (μx) / x!
Where μ = 4
Hence,
[i] P(6;4) = (e^-4)(4^6)/6! =0.104196
[ii] X = 8/1.5 = 5.33
Therefore, P(5.33;4) = (e^-4)(4^5.33)/5.33! = 0.246957
[iii] X = 4/0.5 = 8
Therefore, P(8;4) = (e^-4)(4^8)/8! = 0.02977
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Bibliography
Liu, Z., 2017. Teaching reform of business statistics in college and university. EURASIA
Journal of Mathematics, Science and Technology Education, 13(10), pp.6901-6907.
Mariappan, P., 2019. Statistics for Business. Chapman and Hall/CRC.
Robertson, C. and McCloskey, M., 2019. Business Statistics A multimedia guide to concepts
and applications. Oxford University Press.
Liu, Z., 2017. Teaching reform of business statistics in college and university. EURASIA
Journal of Mathematics, Science and Technology Education, 13(10), pp.6901-6907.
Mariappan, P., 2019. Statistics for Business. Chapman and Hall/CRC.
Robertson, C. and McCloskey, M., 2019. Business Statistics A multimedia guide to concepts
and applications. Oxford University Press.
1 out of 10
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





