A Detailed Structural Analysis of the Sydney Harbour Bridge

This report provides a comprehensive structural analysis of the Sydney Harbour Bridge, covering its history, design, and the engineering principles behind its construction. The analysis includes detailed calculations of dead load, live load, and the effects of wind and temperature. The report explores the support and reaction forces, shear force diagrams, bending moment diagrams, and bending and shear stress distributions across critical sections. It also examines the bridge's balancing nature using the elastic curve equation and discusses miscellaneous issues related to the bridge's structural integrity. The report aims to analyze the bridge's structural behavior using assumed parameters and comparing the old structural analysis methods with the current methods.

Harbour Bridge
1 | P a g e
Mechanics of Structure

Harbour Bridge
Executive Summery
This assignment analyses one of the remarkable structure made by human kind, and it is known
as Harbour Bridge Sydney which is situated in Australia. We have given various assumptions
that how we have measured the different parameter, a brief history and property of this particular
bridge. Further we have analyzed the stress, strain, shear force diagram and bending moment
diagram based on our assumed parameter. We have also analyzed the balancing nature of the
bridge by using elastic curve equation, assumption of dead and alive load were also calculated
according to the traffic and material consumed. Further wind load and temperature effect were
also analyzed specially for this bridge.
2 | P a g e

Harbour Bridge
Contents
Introduction......................................................................................................................................4
Dead Load....................................................................................................................................6
Live loads.....................................................................................................................................6
Support and reaction forces.........................................................................................................7
Calculating shear force................................................................................................................9
Calculating bending moment diagram.......................................................................................10
Bending stress distribution across critical section.....................................................................12
Shear stress distribution across critical section.........................................................................13
Maximum deflection using elastic curve method......................................................................14
Miscellaneous Issue...................................................................................................................17
Conclusion,................................................................................................................................17
Introduction
3 | P a g e

Harbour Bridge
As the time proceeds, Science and technology both developing simultaneously with adding
knowledge and experience in the entire engineering related stream. Analysis of structure is also
one of them. This field becomes more accurate and structural behaviour becomes more
predictable. In the same ways the development of organised society also developed and same
way knowledge of their construction also emerged as important field. This results more
communication and complex traffic system which include small and large bridges, roads and
minimum distance approach phenomena. The gain in knowledge and experience also enhanced
the support in safety and loads of traffic passing through theses bridges.
Once again we have to analyse one the old but famous bridge with my structural analysis point
of view. The motivation and objective behind this work is directly comes from O’Connor 2017
statement, and it is “The steps leading to the introduction of new design loads and other major
changes in codes of practice must include a comparison with older codes and some study of the
performance and strength of existing structures” (O Connor, 2017).”
As stated earlier we have selected a bridge for our analysis purposes, and the bridge we have
selected is nothing but Harbour Bridge of Sydney.
The main reason behind selecting this bridge is level of structural engineering at that time, when
structure analysis is not as easy as present days; certainly this design was implement on the basis
of hand calculation and not with the help of computer and software. Before going into
calculation we have to discuss some fact and figure about this bridge. This bridge is previously
4 | P a g e
Figure 1 Harbour Bridge, Sydney

Harbour Bridge
three hinged arch bridge; later the upper hinge was welded and joined. The bridge is made in
such way that the deck is hanging from five steel trusses. The other two hinges are located at the
end of the bridge. To complete this bridge about 50000 tonnes (Calculated later) of steel
consumed. Only for maintenance purposes this structure cost about 19 million AUD every year.
The height of the arch is around 135 m and its length is about 500 m long. The height from the
water level to lower ceiling of bridge is about 50 m. The pylon made in both side is about 90 m
height. In order to maintain the bridge and its surface, it is being replaced after every ten years.
The whole bridge consists of about 6 million rivets; the weight of the rivets alone is around 3200
tonnes of mild steel. The present standard for load calculation which is available in as Australian
code AS 5100 is more complicated that the standard used in 1920. The specified wind load for
harbour bridge is 1.44 K Pa which is slightly higher than present standard, the other data will be
discussed later (AUS Committee, 2017).
This bridge is made solely for the purpose of connecting two town and these towns are Sydney
central district and north shore of Sydney. The trial was started about ten year before the actual
erection by Francis greenway but the person who successfully implement the idea is Chief
engineer John Bradfield, but due to world was this was postponed till 1922, after 1922 the law
was created and voted by parliament of New South Wales and budget was issued. The bridge
was constructed to hold six lanes of traffic, two numbers of tram and double track for railway,
including two separate pathways also. This bridge is noted under widest bridge of long span and
till 50 years back it was the tallest structure in Sydney. The whole world is accepting it as
beautiful engineering design and looks fascinating for thousands of visitors all around the world.
In tender competition the tender was won by Dorman long and company limited. Initial testing
and destruction for small model were testes several times. Since the design software or any
machine like to today is not available as compared to present days, therefore, the calculation part
for bridge were done continuously until the arch is not completed. The material used to make the
pylon is granite and its quantity is about 18000 M3. The length of the four pin used for joining
the end is about 4 meter and about 350 mm in diameter (Anon., 2014).
Now we will proceed slowly to calculation part, as given in assignment, as discussed earlier the
length of the beam is about 500 m long silicon steel material and the rivets used in this is mild
steel of UTS about 450 MPa. The Cross section of the beam is rectangular shape of on measuring
it was found that its length is around 920 mm and width is 610 mm. the thickness of the beam
steel is 12 mm. from given information board it was found that the factor of safety at that time is
2.5 at that time. The same material is being used for hanger of different length. By counting it
was found that there are 48 hanger used for support all over the bridge, 24 from each side. The
minimum height of each truss is 18 m and maximum height is about 60 meter at the centre. The
width of each truss is about 18 m (Anon., 2014).
As per Australian standard the overall weight of the structure within only 2% of contingency, so
our calculation for dead load will proceed accordingly. To calculate the dead load first we have
5 | P a g e

Harbour Bridge
to figure-out material used in making this bridge, total load in distributed on four different
bearing from each corners at the sides, the rated capacity for thrust bearing is given as 20 kN.
Dead Load
The main material used in bridge are Asphalt, Concrete, stone, coke, including floating, Granite,
Steel rolled, Steel cast, Wrought-iron, Cast-iron, Timber, Ironbark or Grey Gum, Rails and
fastenings, Guard rails and fastenings, we the specific density of each material, If we calculate
the total length. From specification given on bridge it was found that on each meter 105 tons of
steel is used
Therefore,
Total load capacity of bearing = 200,000 kN x 4 = 800,000 = 800000 kN.
The total steel weight = 105 x 500 = 52500 tons
As per Australian standard for load the factor of safety for ultimate limit state γ f3 = 1.1 and γfl =
1.05 then total force will be calculated as
52500 x 1.1 x 1.05 = 60637 KN.
The bridge is completely balance therefore 60637 / 4 = 15160 KN on each of the bearing, In
spite of this steel structure the other materials are not used as huge as steel, and bearing capacity
is much greater than steel load, minor load are not assumed in this calculation.
Live loads
The live load consists of load due traffic on the bridge, Impact due to deck system, load due to
wind and load due to temperature.
As per standard limit the specified limit is 9kN / meter, we have estimated the length and width
of bridge is about 50 x 500 m. Then total uniform distributed load for the traffic. The notional
length width is 3.8 meter specified, in this condition there are thirteen notional lanes is available.
The rail lane is considered as full load lane and rest eleven lane is supposed to be carrying 1/3 of
UDL.
Full load lane = 9 * 500 * 2 = 9000 KN
Rest eleven lane = 3 * 11* 500 = 16500 KN
Total Load = 9000 + 16500 = 25500 KN
6 | P a g e

Harbour Bridge
After multiplying factor of safety = 25500 x 1.1x1.5 = 29452 KN
After adding the dead load = 29452 + 60637 = 900900 KN
This is still less than 800000 KN
Now I have to consider temperature and wind
It is clear that there no hindrance in thermal expansion upward, we also know that the coefficient
for thermal expansion for steel is α = 12 * 10-6 / OC. It assumed that maximum temperature
difference is 25 oC in Sydney.
Δ L=12 x 10−6 x 135 x 25
On calculation, the arch of the bridge can expand vertically up to 40.5 mm.
The horizontal expansion can be calculated as given below
Δ L=12 x 10−6 x 500 x 25=0.15 = 150 mm
From specification, it was found that the deck can be expanded by 400 mm; the calculated
expansion is quit less than the allowed expansion.
As per Australian standard load the allowable air pressure is calculated with the formula
Vd = Sg x Vs
For specific place Sydney, the wind load Vd is specified as = 55 kN/cubic meter.
Support and reaction forces
Near the pylon we can see that each support is hinged at
an angle of around 45o. In such condition all the loads
trying to make the arch in horizontal straight, but it is
supported on hinged approach so all load comes to this
four hinges, we can calculate the total load on each
hinge
7 | P a g e
Figure 2 Hinge support

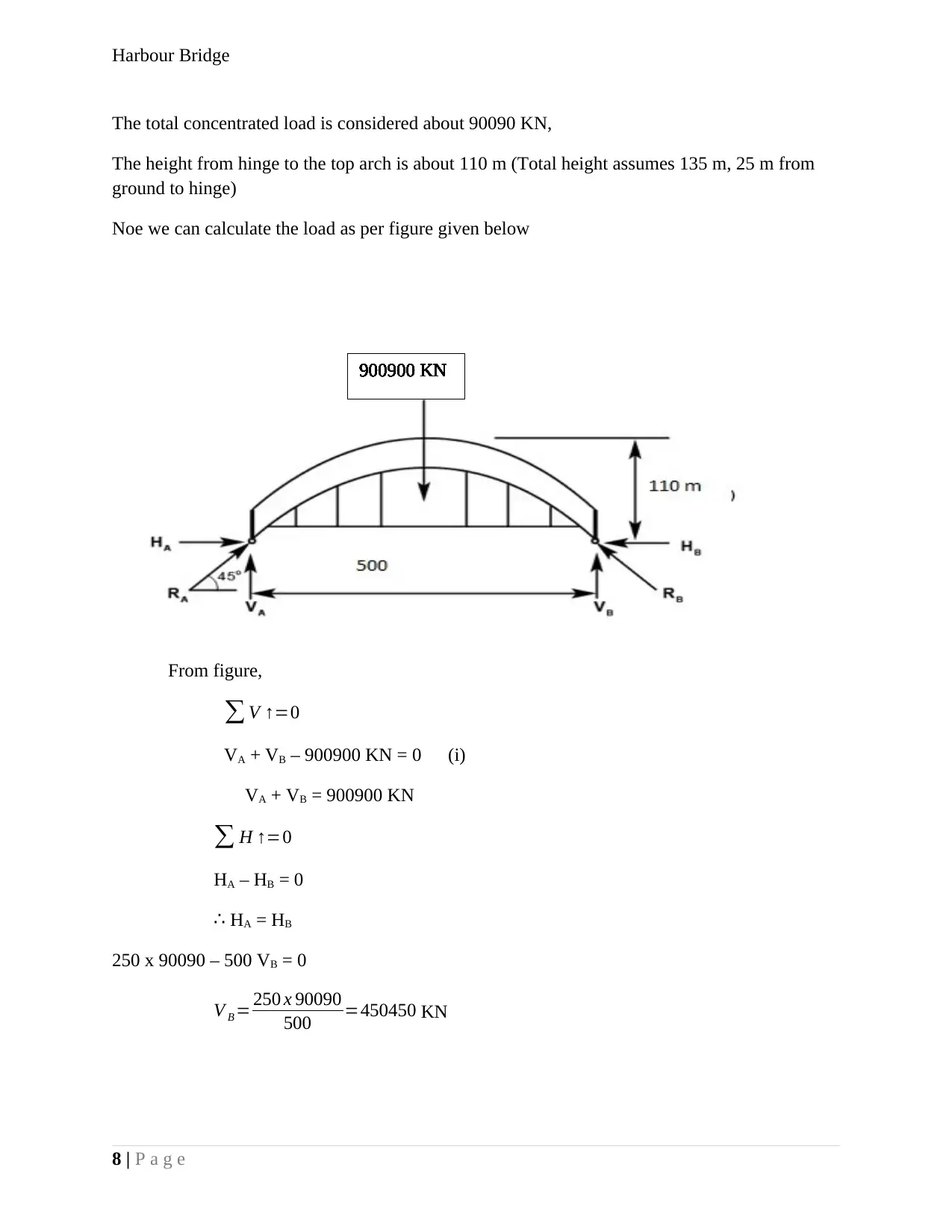
Harbour Bridge
The total concentrated load is considered about 90090 KN,
The height from hinge to the top arch is about 110 m (Total height assumes 135 m, 25 m from
ground to hinge)
Noe we can calculate the load as per figure given below
From figure,
∑ V ↑=0
VA + VB – 900900 KN = 0 (i)
VA + VB = 900900 KN
∑ H ↑=0
HA – HB = 0
∴ HA = HB
250 x 90090 – 500 VB = 0
V B = 250 x 90090
500 =450450 KN
8 | P a g e
900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN900900 KN

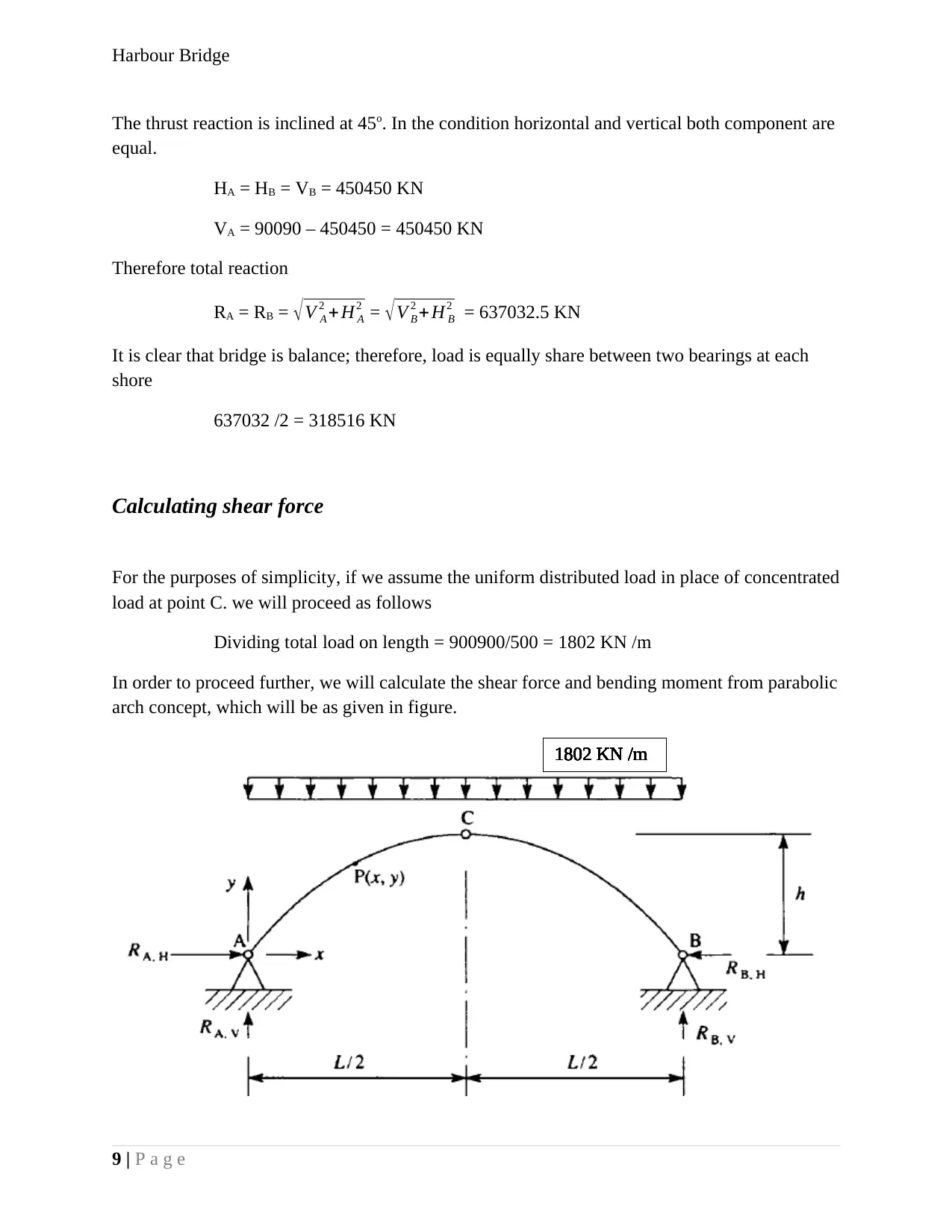
Harbour Bridge
The thrust reaction is inclined at 45o. In the condition horizontal and vertical both component are
equal.
HA = HB = VB = 450450 KN
VA = 90090 – 450450 = 450450 KN
Therefore total reaction
RA = RB = √V A
2 + H A
2 = √V B
2 + H B
2 = 637032.5 KN
It is clear that bridge is balance; therefore, load is equally share between two bearings at each
shore
637032 /2 = 318516 KN
Calculating shear force
For the purposes of simplicity, if we assume the uniform distributed load in place of concentrated
load at point C. we will proceed as follows
Dividing total load on length = 900900/500 = 1802 KN /m
In order to proceed further, we will calculate the shear force and bending moment from parabolic
arch concept, which will be as given in figure.
9 | P a g e
1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m1802 KN /m

Harbour Bridge
The force on vertical direction = RAV = RBV= 1802 *500/2 = 450450 KN
And if the horizontal is absent then RAH = RBH
Now I have to calculate moment forces abut C from left side
RAH *h – RAV x L/2 + wL2/8 = 0
Or RAH = wL2/8h = 1802 x 500 x 500/(8x 110) = 511932 KN
When A is assumed as axis, the equation for parabola cane be written as
y= 4 h
L2 (Lx−x2)
Bending moment can be given by at any point P (x,y) for parabolic arch
Mp=RAV . x – RAH . y – w x2
2
Putting the value of RAV and RAH for x in place of y
M P = wL
2 x− w L2
8 h . 4 h
L2 ( Lx−x2 )− w x2
2
After simplification
M P = wL
2 x− wL
2 x − w x2
2 − w x2
2 =0
At nay section of arch the shear force should always be zero for design.
Calculating bending moment diagram
10 | P a g e
180218021802180218021802180218021802180218021802180218021802180218021802

Harbour Bridge
It is clear that the load of the arch carries load at point C
In this condition the bending moment at any point between A and C may be calculated as follows
M p 1=RAV x−R AH y ……… (i)
And for bending moment at any point between C and B is
M p 1=RAV x−W ( x−x ❑c ) −R AH y ….. (ii)
And bending moment for the point in the middle = RAH*h = 900900 x 110 = 99099000 KNM
The shape of bending moment diagram will be as given above.
Bending stress distribution across critical section
As we know that trusses used in bridge is used to transmit the loads of the bridge to the support,
it is basically used to load the dead and live loads of the bridges, and transfer the load to the
hinges and finally to the ground. We already know that their shape depends upon the requirement
of transferring loads. For Harbour Bridge, the shape used is triangular base with varying shape
and cross section of the beams; its trusses are name as Warrnen truss. The joint of the truss is
fixed with pin and finally with hydraulics which adjust the thermal movement of the whole
bridge. The material used for warren truss is not silicon steel rather it is mild steel, which more
capable of carrying the load as compared to silicon steel which is more stringer than mild steel.
11 | P a g e

Harbour Bridge
For load distribution, it is difficult to calculate the bending moment of all the trusses used in
Harbour Bridge but it can be simplified and formulated in smaller section and finally integrated
to whole span. The figure given below is similar to the trusses used in Harbour Bridge but it is of
one section. The span consist of 56 trusses including both side
Figure 3- Truss in Harbour Bridge
As we see that in the figure, this just for illustration, we have to calculate reaction at the support.
If we tale moment about a. The reaction force A is not known for the present condition, we have
to calculate it first for 145 KN force. As we know that the all the system is in equilibrium
Then, ∑ M A =0
The bending moment will be
0=(180 x 0.5)+(110 x 1.5)+(145sin75o x 2.5) – (145Cos75o x 0.866) – 3RB
3RB = 90 + 165 +140.05 –32.4975 = 362.55 KNM
RB = 362.55/3 = 120.85 KN
Now I have to find vertical force
∑ FV =0
0 = 180 – 110 – 145Sin75 + 120.85 + RAV
Or, , RAV = 50.78
The horizontal force will be calculated as
RAH = 145Cos75 = 145 *0.2588 = 37.526 KN
Now the reaction force RA can be calculated as follows
RA = √ 120.852+ 37.5262=126.5422 KN
12 | P a g e

Harbour Bridge
Shear stress distribution across critical section
Now I have to calculate distribution of forces in member of truss such as X and Y
Total vertical forces upon X can be calculated as
∑ FV =0 = 120.85 –Fx.Sin 60o
Therefore FX =120.85 ¿=139.55
The forces acting on the X direction will be 139.55 KN and it is compressive force
Total vertical forces upon Y can be calculated as
∑ FY =0 = 50.78 –139.55cos 60o
FY =50.78−139.55∗0.5=−18.99 KN
The forces acting on the Y direction will be -18.99 KN and it is in tension
Similarly we can that calculate the forces and direction of the entire truss, which is in 52
numbers. To calculate the all the beams tension of compression takes too long, but the process is
as similar as given above. The main point behind this calculation is that we can see the direction
and magnitude of all the forces transferring towards base of the bridge.
As we can see that distribution of shear stress is also used in above calculation
Maximum deflection using elastic curve method
Since Macaulay method is only suitable for cantilever beam, therefore we to use elastic curve
method.
Again we have to consider the whole bridge as force of uniform distributed load of about 1800
KN/m. We have studied earlier that, at point P, the curvature of a plane curve can be represented
as the formula
13 | P a g e

Harbour Bridge
1
ρ =
d2 y
d x2
[1+ ( d2 y
d x2 )2
]3
2
As given in equation is well know that dy/dx is first order derivative and its second
order derivative will be d2y/dx2 , the function y(x) that is equation of a curve, but one thing we
have to note in this equation that the slope dy/dx as small as negligible, and further its square is
more negligible, there the equation ma becomes as follows
1
ρ = d2 y
d x2
From mechanics and strength of material it is clear that 1
ρ = M(x)/EI
This is the equation of the second order linear differential equation and also known as elastic
curve. The denominator term EI is known as flexural rigidity and it variation is according to the
beam. The beam we have selected also known as prismatic beam and for this kind of beam the EI
is considered as constant (Gere, 2014).
The final deflection can be achieved by double integrating the equation as follows
EI y=∫
0
x
dx∫
0
x
M ( x ) dx +C1 x+ C2
14 | P a g e
Figure 4 - Deflection calculation for Harbour Bridge

Harbour Bridge
We know that C1 is first constant and C2 is second constant, these constant can be determined
according to the boundary condition given for particular situation. The bridge is supposed to as
given in figure with uniform distributed load. As per above figure the moment of the AD part
about D will be given as M = 1
2 WLx− 1
2 w x2
If we place the moment equation is above integral part the we can see that
EI . d2 y
d x2 =−1
2 W x2+1 /2 WLx
If we integrate the twice the above equation we will get as follows
EI dy
dx =−1
6 W x2 + 1
4 WL x2+C1
And in second integration
EI y=−1
24 W x4 + 1
12 WL x3+ C1 x+C ❑2 …….(i)
Now I have to calculate the constant C1 and C2, for this we have to analyse the given condition,
If y = 0, the beam end from both side, y =0, if we put x =0 and y =0 in equation (i) we
get C2 = 0, we than analyse it as x = L and y = 0 in the equation (i) then
0=−1
24 W L4 + 1
12 W L3 +C1 L
¿ , C1 =−1
24 W L3
Now after putting the value of C1 and C2 in the equation we obtain it as
EI y=−1
24 W x4 + 1
12 WL x3− 1
24 W L3 x
¿ , y= W
24 EI (−x4 +2 L x3 −L3 x )
If we place the value of first integration then we can see that the slope of the beam becomes zero
at the point L/2, the second thing we obtain from equation is that elastic curve has minimal value
at the midpoint that is C. Putting the value x = L/2, we have
15 | P a g e

Harbour Bridge
ymax= W
24 EI (−L4
16 + 2 L L3
8 −L3 L
2 )=−5 W L4
384 EI
Therefore, the maximum defections can be obtained from the Harbour bridge = −5 W L4
384 EI
Now in order to find the deflection we have to find I of the bridge about D
I y= W d3
12 (Where D is thehight of the beam)
From the construction of the bridge it was found that beam is considered from bottom
surface to surface of road about 4.2 meter and width of the beam is 50 m. The elastic constant for
steel is for ASTM –A36 = 200 GPa
First we will calculate the
I y =50 x 43
12 =¿ 266.67 kg.m2
Elastic constant = 200 GPa = 200 * 109 Pa
W = 50 m
L = 500 m
Now we can calculate deflection from the formula = −5 W L4
384 EI
Putting the value in above equation
y=−5∗91930 x 1000 5004
384∗200∗109 x 266∗1000
y=−1.40626 m=−1406.26mm
Therefore, as per calculation, the deflection in beam will be 1406 mm. It means that when the
bridge is fully loaded, it can deflection downward about 1406 mm. in order to avoid the
16 | P a g e

Harbour Bridge
downward in every bridge we are providing sag value by giving the tension in the rope and
lifting it upward direction, the shape of bridge is little crown shape i.e. middle portion is upward.
Miscellaneous Issue
It is clear from the calculation also that the capacity of the bridge is quite more than what vehicle
is the loaded on it, During the construction time the standard was even simpler and lower, In
today’s scenario we can make 1.5 similar bridge with same span. The use of new kind of steel in
this bridge also opened the way to use it other places of bridge. But one thing is not taken care
and that is corrosion. This is the reason that this bridge was painted on every five years, actually
time elapsing to complete the painting is five years, and therefore we can say that after
completion of painting each time, they start painting for next time. After start of operation, this
bridge were studied several time till date, for further reinforcement, but this bridge is so stable
that there is not suggestion accepted for any further reinforcement. One of the main problems
with this bridge is that it cannot be further expanded, but harbour tunnel made near this bridge
helping it to reduce the traffic jam on this bridge.
Conclusion,
From above analysis, and calculation one thing is clear that making a bridge like Harbour Bridge
or even shorter bridge require enormous amount of calculation and analytical skill. Certainly
there may be a gap between my calculation by assuming the different parameters and actual
calculation, during making of this bridge. From my stress analysis it was found that the reaction
at each of the pylon containing bearing is about 318516 KN which quite less than 20, 000 ton or
196000000 KN, the bending moment also calculated at central load and uniform distributed load
9909900 KNM which also seems it has better stability than it is designed for the purpose. Stress
distribution in each Struss is also seems to appropriate, because of the variety of length and
shapes used as beams for Struss, the stress calculation for each of the beam in arch is not
possible in present condition. The deflection in the beam due to dead and live load is 1.4 m
which is also normal for such kind of bridge; this deflection is countered by giving sag value in
central upper arch of bridge and provides more tension to rope in the middle part. From my point
of view, this bridge has consumed more than necessary material, at present we are using less
material for making such kind of bridge. The continuous development and research helped us to
achieved optimum use of material and energy. But as per time and availability present in second
decade of nineteenth century this bridge is marvellous example of engineering.
17 | P a g e

Harbour Bridge
Referencing
Agro, D, 2011. Principle of stress and strain, Strength of materials, 1(1), pp. 1-20.
Andrew Pytel, J, K, 2001, Engineering Mechanics: Dynamics. 2nd ed. london: Thomson
Learning.
Anon, 2014, SydneyHarbour.html. [Online]
Available at: http://www.bristol.ac.uk/civilengineering/bridges/Pages/NotableBridges/
SydneyHarbour.html
[Accessed 15 10 2017].
AUS Committee, 2017, Australian Standard Bridge design: AS 5100.7:2017, Sydney: Standard
Australia.
Bacidore, M, 2014, vibration analysis can detect alignment problems, Wolters Kluwer: Hughes
Communications.
Bird, J, & Ross, C., 2012, Linera momentum and impulse, 2nd ed. London: Taylor and Francis.
Dunn, D, 2011, Complex Stress. Mechnical properties of materials, 1(3), pp. 1-22.
Gere, J, 2014, Mechanics of Materials, Brief Edition, 4th edition ed. Stamford: Cengage.
Hartog, J, P, D, 2012. Strength of Materials. 8th ed. New York: Dover Publication.
Hibbler, 2010, Engineering Mechanics: Combined Statics & Dynamics. 12th ed. London:
Prentice Hall.
J, L, Meriam, L, G, K, 2012. Engineering Mechanics: Dynamics. 7th ed. Denever: John Wiley.
Lange, A, 2009, Simple stress and strain. 1(1), pp. 1-286.
18 | P a g e

Harbour Bridge
Negi, L, S, 2007. Strength of Materials, 1 ed. New york: Sigma Publisher.
O Connor, R, 2017, Analysis of the design of experiments of bridges. Procedia Structural
Integrity, 5(1), pp. 1-7.
Robalo, B, 2013. Structural analysis of steel bridge decks. Tecnico lisboa, 1(1), pp. 1-150.
Roylance, D, 2008. Mechanical Properties of material, Mechanical Engineering Journal, 1(1),
pp. 1-128.
Taratori, S, 2008, Critical analysis of design and consruction. Bridge Engineering 2, 1(1), pp. 1-
10.
APPENDICES
19 | P a g e

Harbour Bridge
20 | P a g e

Harbour Bridge
21 | P a g e