Mathematical Investigation Report: Sydney Harbour Bridge Analysis
VerifiedAdded on 2022/11/23
|5
|1528
|468
Report
AI Summary
This report presents a comprehensive mathematical investigation of the Sydney Harbour Bridge. The investigation focuses on calculating the length of steel cables required for its construction. Utilizing quadratic equations, the report analyzes the bridge's parabolic shape, determining the height and length at various points. The analysis includes finding the vertex form, x-intercepts, and discriminant of the quadratic equation representing the bridge's arch. The report also explores the width of the sea level and identifies key geometric shapes. Through detailed calculations and analysis, the report aims to provide a clear understanding of the mathematical principles underlying the bridge's design and construction, including the use of vertex and standard forms to model the bridge structure.

Sydney Harbour Bridge
Mathematical Investigation Report
Abstract: The bridge is an arch made of steel. An arch bridge made of steel. It is located in
Sydney, Australia and crosses port Jackson. The locals had also nicknamed it as The Coat hanger
because of it shape. The idea of connecting the Sydney central business district and the north
shore was dated back to 1815 when firstly Francis Greenway proposed it. But nothing happened
until after a century when, in 1912, John Bradfield was appointed as the chief engineer of the
bridge project. Unfortunately, the World War I postponed the construction. Finally, in November
1922, the needed laws for the construction of the bridge were voted by the New South Wales
parliament.
The competition for construction tenders took place the same year and the British firm Dorman
Long and Co Ltd, Middlesbrough won it the next year with the design of an arch bridge. The
bridge finished and opened ten years later, in 19 March 1932. The original designer of the bridge
is John Job Crew Bradfield. But it was Sir Ralph Freeman who was appointed by the company to
design the model in further detail. In fact, there was an argument between them for who actually
designed it. Also Arthur Plunkett proposed three different schemes to the company. The engineer
of the project was Gilbert Roberts and the consulting engineer was Georges Camille Imbault. It
was constructed to hold six lanes of traffic, two lanes for trains, two lanes for trams and two
footpaths. Its deck is still the widest for a long span bridge and tallest steel arch bridge. It was
also the tallest structure in Sydney until 1967.
Introduction:
Aim
The aim of this investigation is to calculate the length of steel cable required for the construction
of the bridge.
The Sydney Harbour Bridge will be used to investigate a diverse number of points in the
structure such as the height and length. Quadratics will be used to solve the height of the bridge
at different points on the x axis.
A quadratic is an equation constructed from information collected from a graph; this equation
can also be used to produce a graph. Quadratics can be used to solve the problem dealt in this
investigation as the Sydney Harbour Bridge is identified as a parabola shape. Only basic
information is given about the bridge and the answers can be established by solving the
additional questions. The quadratic equation will be tested from the graph to prove the accuracy
of the quadratic identified. Quadratics are mainly seen in the form ax^2+bx+c=0, where x is a
variable of any number.
The bridge is mounted on two base pylons on the opposite ends. The highest point of the bridge
is 182.5cm above sea level and the longest vertical cable is 135m from the origin. This position
is the vertex, which is the highest or lowest point inside a quadratic, and in this case it is highest
in this scenario. The axis of symmetry is an imaginary vertical line that cuts through and splits
both sides evenly on the graph. The main supporting arc has 2 points that sits on the road situated
50m above sea level.
Mathematical Investigation Report
Abstract: The bridge is an arch made of steel. An arch bridge made of steel. It is located in
Sydney, Australia and crosses port Jackson. The locals had also nicknamed it as The Coat hanger
because of it shape. The idea of connecting the Sydney central business district and the north
shore was dated back to 1815 when firstly Francis Greenway proposed it. But nothing happened
until after a century when, in 1912, John Bradfield was appointed as the chief engineer of the
bridge project. Unfortunately, the World War I postponed the construction. Finally, in November
1922, the needed laws for the construction of the bridge were voted by the New South Wales
parliament.
The competition for construction tenders took place the same year and the British firm Dorman
Long and Co Ltd, Middlesbrough won it the next year with the design of an arch bridge. The
bridge finished and opened ten years later, in 19 March 1932. The original designer of the bridge
is John Job Crew Bradfield. But it was Sir Ralph Freeman who was appointed by the company to
design the model in further detail. In fact, there was an argument between them for who actually
designed it. Also Arthur Plunkett proposed three different schemes to the company. The engineer
of the project was Gilbert Roberts and the consulting engineer was Georges Camille Imbault. It
was constructed to hold six lanes of traffic, two lanes for trains, two lanes for trams and two
footpaths. Its deck is still the widest for a long span bridge and tallest steel arch bridge. It was
also the tallest structure in Sydney until 1967.
Introduction:
Aim
The aim of this investigation is to calculate the length of steel cable required for the construction
of the bridge.
The Sydney Harbour Bridge will be used to investigate a diverse number of points in the
structure such as the height and length. Quadratics will be used to solve the height of the bridge
at different points on the x axis.
A quadratic is an equation constructed from information collected from a graph; this equation
can also be used to produce a graph. Quadratics can be used to solve the problem dealt in this
investigation as the Sydney Harbour Bridge is identified as a parabola shape. Only basic
information is given about the bridge and the answers can be established by solving the
additional questions. The quadratic equation will be tested from the graph to prove the accuracy
of the quadratic identified. Quadratics are mainly seen in the form ax^2+bx+c=0, where x is a
variable of any number.
The bridge is mounted on two base pylons on the opposite ends. The highest point of the bridge
is 182.5cm above sea level and the longest vertical cable is 135m from the origin. This position
is the vertex, which is the highest or lowest point inside a quadratic, and in this case it is highest
in this scenario. The axis of symmetry is an imaginary vertical line that cuts through and splits
both sides evenly on the graph. The main supporting arc has 2 points that sits on the road situated
50m above sea level.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
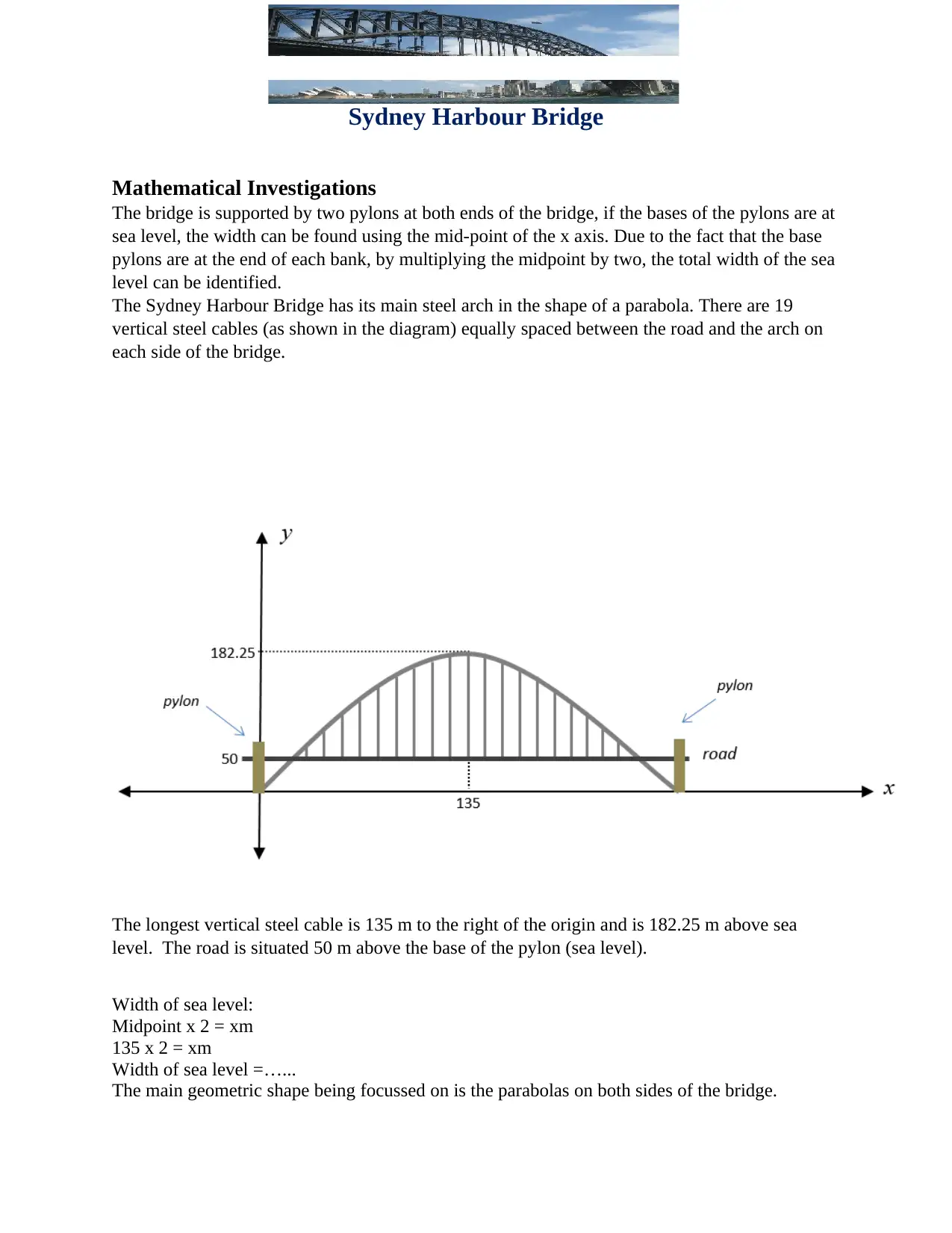
Sydney Harbour Bridge
Mathematical Investigations
The bridge is supported by two pylons at both ends of the bridge, if the bases of the pylons are at
sea level, the width can be found using the mid-point of the x axis. Due to the fact that the base
pylons are at the end of each bank, by multiplying the midpoint by two, the total width of the sea
level can be identified.
The Sydney Harbour Bridge has its main steel arch in the shape of a parabola. There are 19
vertical steel cables (as shown in the diagram) equally spaced between the road and the arch on
each side of the bridge.
The longest vertical steel cable is 135 m to the right of the origin and is 182.25 m above sea
level. The road is situated 50 m above the base of the pylon (sea level).
Width of sea level:
Midpoint x 2 = xm
135 x 2 = xm
Width of sea level =…...
The main geometric shape being focussed on is the parabolas on both sides of the bridge.
Mathematical Investigations
The bridge is supported by two pylons at both ends of the bridge, if the bases of the pylons are at
sea level, the width can be found using the mid-point of the x axis. Due to the fact that the base
pylons are at the end of each bank, by multiplying the midpoint by two, the total width of the sea
level can be identified.
The Sydney Harbour Bridge has its main steel arch in the shape of a parabola. There are 19
vertical steel cables (as shown in the diagram) equally spaced between the road and the arch on
each side of the bridge.
The longest vertical steel cable is 135 m to the right of the origin and is 182.25 m above sea
level. The road is situated 50 m above the base of the pylon (sea level).
Width of sea level:
Midpoint x 2 = xm
135 x 2 = xm
Width of sea level =…...
The main geometric shape being focussed on is the parabolas on both sides of the bridge.

Sydney Harbour Bridge
Standard form: y = 0.0022x^2 + 139
Vertex form: y-139 = -0.0022x^2
To find the vertex form of the parabola, firstly find the vertex which is (0.139). but since (h, k) is
the vertex in the y-k = a (x-h) ^2;
The factored form is;
Y = -0.0022(x + 251.5) (x-251.5)
To find the factored form of the parabola, lets first find the x-intercepts which are (-251.5, 0) and
(251.5, 0)
Focus and directrix:
In standard form;
y = -0.0022x^2 + 139
vertex;
(-b/2a, (4ac-b^2)/4a = (0, 139)
Focus;
(-b/2a, c+((1-b^2)/4a) = (0, 25.36)
Directrix:
Y = c-(b^2 + 1)/2a = y = 366.27
This steel structure was opened on March 19th, 1932 after 6 years of construction. It carries eight
vehicle lanes, two train lines, a footway and a cycleway. The opening celebrations included a
vast cavalcade of decorated floats, marching groups and bands proceeding through the city
streets and across the deck in a pageant of surprising size and quality, considering the economic
depression.
According to my research, the height of the bridge is 139m. So then, the point (0,139) is on my
parabola, the vertex. The y-axis will be the at the middle of the bridge, and the span is 503 feet, I
divided 503 by 2, so is 251.5. so the x-intercept is -251.5 and 251.5. I got all the point to get my
equation.
y= -0.0022x^2+139. This equation is in standard form.
Standard form: y = 0.0022x^2 + 139
Vertex form: y-139 = -0.0022x^2
To find the vertex form of the parabola, firstly find the vertex which is (0.139). but since (h, k) is
the vertex in the y-k = a (x-h) ^2;
The factored form is;
Y = -0.0022(x + 251.5) (x-251.5)
To find the factored form of the parabola, lets first find the x-intercepts which are (-251.5, 0) and
(251.5, 0)
Focus and directrix:
In standard form;
y = -0.0022x^2 + 139
vertex;
(-b/2a, (4ac-b^2)/4a = (0, 139)
Focus;
(-b/2a, c+((1-b^2)/4a) = (0, 25.36)
Directrix:
Y = c-(b^2 + 1)/2a = y = 366.27
This steel structure was opened on March 19th, 1932 after 6 years of construction. It carries eight
vehicle lanes, two train lines, a footway and a cycleway. The opening celebrations included a
vast cavalcade of decorated floats, marching groups and bands proceeding through the city
streets and across the deck in a pageant of surprising size and quality, considering the economic
depression.
According to my research, the height of the bridge is 139m. So then, the point (0,139) is on my
parabola, the vertex. The y-axis will be the at the middle of the bridge, and the span is 503 feet, I
divided 503 by 2, so is 251.5. so the x-intercept is -251.5 and 251.5. I got all the point to get my
equation.
y= -0.0022x^2+139. This equation is in standard form.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Sydney Harbour Bridge
Vertex:
The Vertex of my parabola is (0,139). Is the maximum of my parabola, the highest point? Also in
the equation y-139=-0.0022(x)^2 the vertex is (h,k) which is (0,139). The vertex is the highest
point of my parabola, or the height. The equation of axis symmetry is x=0. And we know it's
open down, because the a in the equation is negative.
Y- intercept:
The y-intercept of my parabola is 139, my parabola cross the y-axis at 139. Or u can find it in the
equation (standard form) y=-0.0022x^2+139. the 139 is the y- intercept. The y intercept is the
highest point of my bridge.
Discriminant:
The standard of my parabola is y=-0.0022x^2 +139. The discriminant is square root of 0^2 - 4*-
0.0022c*139. is 1.2232, my parabola has two solutions, is an irrational number. So the
polynomial -0.0022x^2 +139 cannot be factored into linear factors with integer coefficients.
X intercept:
there are 2 x-intercepts, and that if we tried to use the quadratic formula to find the x-intercepts,
there would be 2 solutions. I could also tell just by looking at the graph that there are 2 x-
intercepts, (251.5,0) (-251.5,0). So my parabola cross the X axis twice.
Equation Cont'd
y = f(x) = Ax^2 + Bx + C is the quadratic function
(0,0) <--- left endpoint of the bridge
(1650,0) <--- right endpoint of the bridge
1650/2 = 825
(825, 440) <--- this is the vertex
(0,0) ---> C=0
So the quadratic function becomes
y = f(x) = Ax^2 + Bx
0 = A (1650) ^2 + 1650B = 2722500A + 1650B
Vertex:
The Vertex of my parabola is (0,139). Is the maximum of my parabola, the highest point? Also in
the equation y-139=-0.0022(x)^2 the vertex is (h,k) which is (0,139). The vertex is the highest
point of my parabola, or the height. The equation of axis symmetry is x=0. And we know it's
open down, because the a in the equation is negative.
Y- intercept:
The y-intercept of my parabola is 139, my parabola cross the y-axis at 139. Or u can find it in the
equation (standard form) y=-0.0022x^2+139. the 139 is the y- intercept. The y intercept is the
highest point of my bridge.
Discriminant:
The standard of my parabola is y=-0.0022x^2 +139. The discriminant is square root of 0^2 - 4*-
0.0022c*139. is 1.2232, my parabola has two solutions, is an irrational number. So the
polynomial -0.0022x^2 +139 cannot be factored into linear factors with integer coefficients.
X intercept:
there are 2 x-intercepts, and that if we tried to use the quadratic formula to find the x-intercepts,
there would be 2 solutions. I could also tell just by looking at the graph that there are 2 x-
intercepts, (251.5,0) (-251.5,0). So my parabola cross the X axis twice.
Equation Cont'd
y = f(x) = Ax^2 + Bx + C is the quadratic function
(0,0) <--- left endpoint of the bridge
(1650,0) <--- right endpoint of the bridge
1650/2 = 825
(825, 440) <--- this is the vertex
(0,0) ---> C=0
So the quadratic function becomes
y = f(x) = Ax^2 + Bx
0 = A (1650) ^2 + 1650B = 2722500A + 1650B
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Sydney Harbour Bridge
440 = A (825) ^2 + (825) B
440 = 680625A + 825B
The two equations are:
0 = 2722500A + 1650B
440 = 680625A + 825B
Multiplies second equation by -4 and adds it to the first equation:
-1760 = -1650B
B = -1760/-1650 = 176/165 = 16/15
Per the first equation: 0 = 2722500A + 1650(16/15)
0 = 2722500A + 1760
A = -1760/2722500 = -160/247500
= -16/24750
= -8/12375
y = f(x) = ( -8/12375) x^2 + (16/15) x
440 = A (825) ^2 + (825) B
440 = 680625A + 825B
The two equations are:
0 = 2722500A + 1650B
440 = 680625A + 825B
Multiplies second equation by -4 and adds it to the first equation:
-1760 = -1650B
B = -1760/-1650 = 176/165 = 16/15
Per the first equation: 0 = 2722500A + 1650(16/15)
0 = 2722500A + 1760
A = -1760/2722500 = -160/247500
= -16/24750
= -8/12375
y = f(x) = ( -8/12375) x^2 + (16/15) x
1 out of 5
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
