Cryptography Assignment: Symmetric, Asymmetric Encryption Explained

This assignment provides an overview of cryptography, focusing on symmetric and asymmetric encryption methods. It explains the core concepts, including the use of a single secret key in symmetric encryption and complementary key pairs in asymmetric encryption. The document details key exchange methods like Diffie-Hellman and covers algorithms such as RSA, DES, and AES, as well as stream and block ciphers. It also explains the principles of confusion and diffusion, critical elements in cryptographic design. The DES algorithm, including its limitations and the evolution to Triple DES, is discussed. Finally, the assignment provides an overview of AES (Advanced Encryption Standard), highlighting its use of transposition and substitution cycles.

Week 2 Lecture 1 - Cryptography 2 1
Week 2 Lecture 1 -
Cryptography 2
Symmetric Encryption
If the encryption and decryption keys are the same, then
That is, the decryption, via the key, of the encryption, via the key, of the
plaintext is the plaintext. This is known as Symmetric Encryption.
Converting the ciphertext back into the plaintext requires a separate process.
Symmetric algorithms use one key, a secret key encryption but for an N-user
system, we would require n(n-1)/2 keys for each pair of users.
Asymmetric Encryption
Asymmetric Encryption implies the keys are in complementary pairs. A
decryption key, , inverts the encryption key .
In public key or asymmetric encryption, each user has two keys: a public and a
private key. The public key is published freely because it is only one half of an
inverse pair.
The public key encryption is decrypted via the private key.
The private key encryption is decrypted via the public key. Multiple users can
send messages privately to each other using public keys.
Diffie-Hellman Key Exchange
Diffie and Hellman published the first paper on public key cryptography where
a sender and receiver use simple arithmetic to exchange keys.
There are three conditions:
It must be computationally easy to encode/decode with a key.
P = D(K, E(K, P ))
K D K E
P = D(K , E(K , P ))D E
P = D(K , E(K , P ))private public
P = D(K , E(K , P ))public private

Week 2 Lecture 1 - Cryptography 2 2
It must be computationally infeasible to derive the private key from the
public key.
It must be computationally infeasible to determine the private key from a
plaintext attack
Mathematically we require to find k such that
Where p is prime and g 0,1 or p-1, g and p are agreed a priori.
RSA
The RSA cryptosystem is a public-key system that has been a de-facto
standard for many years.
where and are prime numbers. The totient (n) is the number of numbers
less than n with no factors in common with ( ) and ( ).
Commercial Needs
When an encryption has to be of a commercial grade, i.e. trustworthy, has to
be based on sound mathematics, be analysed and tested.
Three algorithms have been used in the business world:
DES
AES
RSA
Stream and Block Ciphers
Stream ciphers convert one plaintext character at a time while a block cipher
encyrpts a group of characters at a time and treats this as a single block
entity.
Stream ciphers have low error propagation, because only one character is
encoded at a time, but they can be susceptible to malicious insertions or
modifications. They are fast to encrypt.
Block ciphers are highly diffused, information about a character (or the
plaintext) is spread out in th eciphertext. Errors may be propogated within the
block and encryption is slower. Padding of blocks occurs.
n = g mod pk
n = pq
p q
p − 1 q − 1

Week 2 Lecture 1 - Cryptography 2 3
Confusion and Diffusion
It is not just the cryptographic function itself that hides the original plaintext.
Use is made of the principles of Confusion and Diffusion.
Confusion, according to Shannon, is making the relationship between the key
and the ciphertext as complex as possible. Confusion is simply trying to make
the ciphertext as unreadable as possible.
Diffusion, on the other hand, means that the cipher is spread about the input
characters such that the ouptuts depends on many parts of the input.
DES
The DES is a combination of substitution and transposition and the DES
algorithm repeatedly uses these two techniques for 16 cycles, effectively
diffusing the plaintext.
The plaintext is encrypted as fixed blocks of 65 bits 56 + padding). A
difderent set of 48 bits is manipulated in each of the cycles by arithmetic and
logical operators.
There were many arguements about how much securit DES provided because
of the short key length. In 1998, a DES Cracker Deep Crack) machine broke a
key in 4 days.
Triple DES is the use of 3 keys that encrypt, encrypt again and the re-encrypt
giving a strength of 112 bits.
C = E(k , E(k , E(k , P )))3 2 1

Week 2 Lecture 1 - Cryptography 2 4
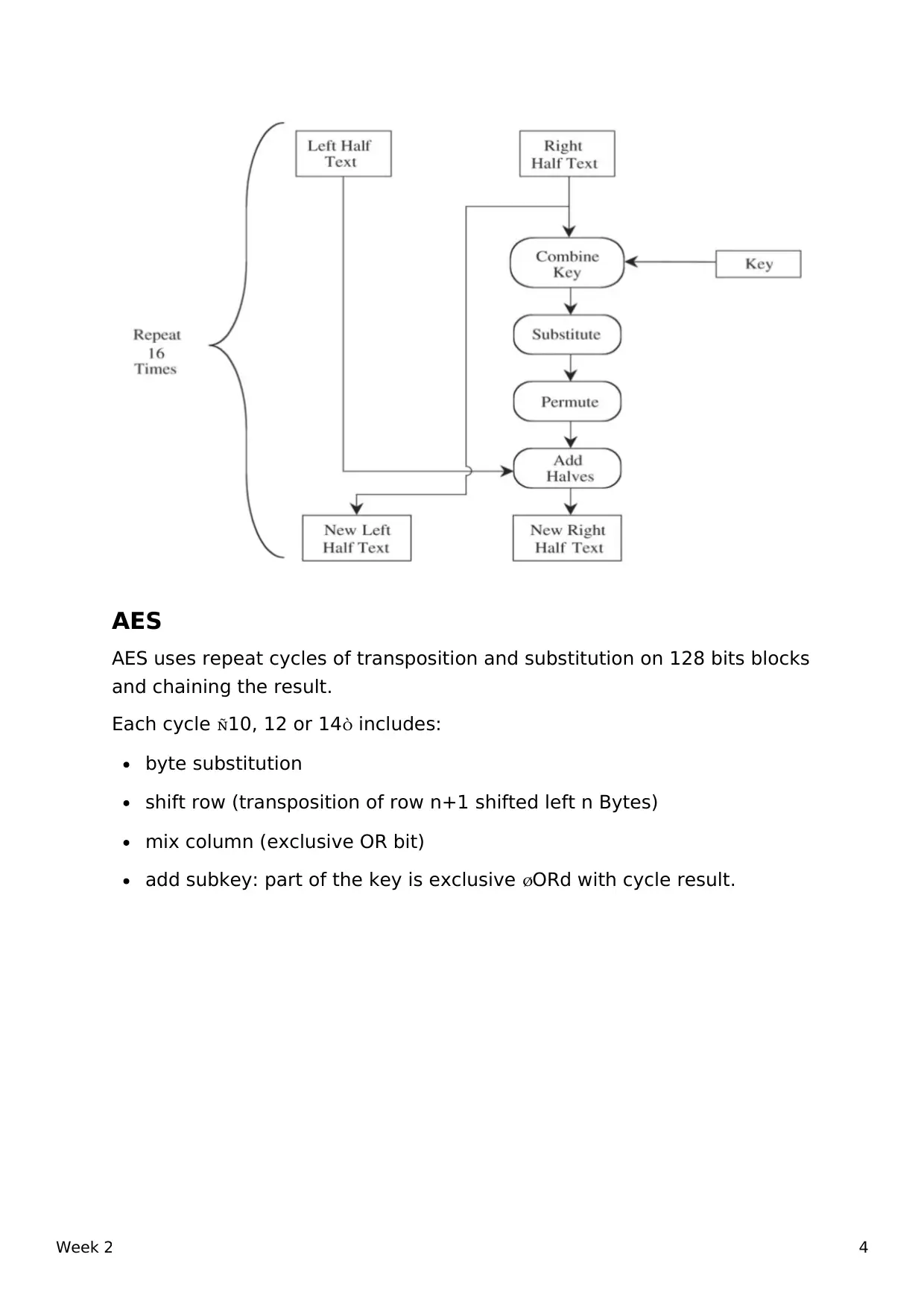
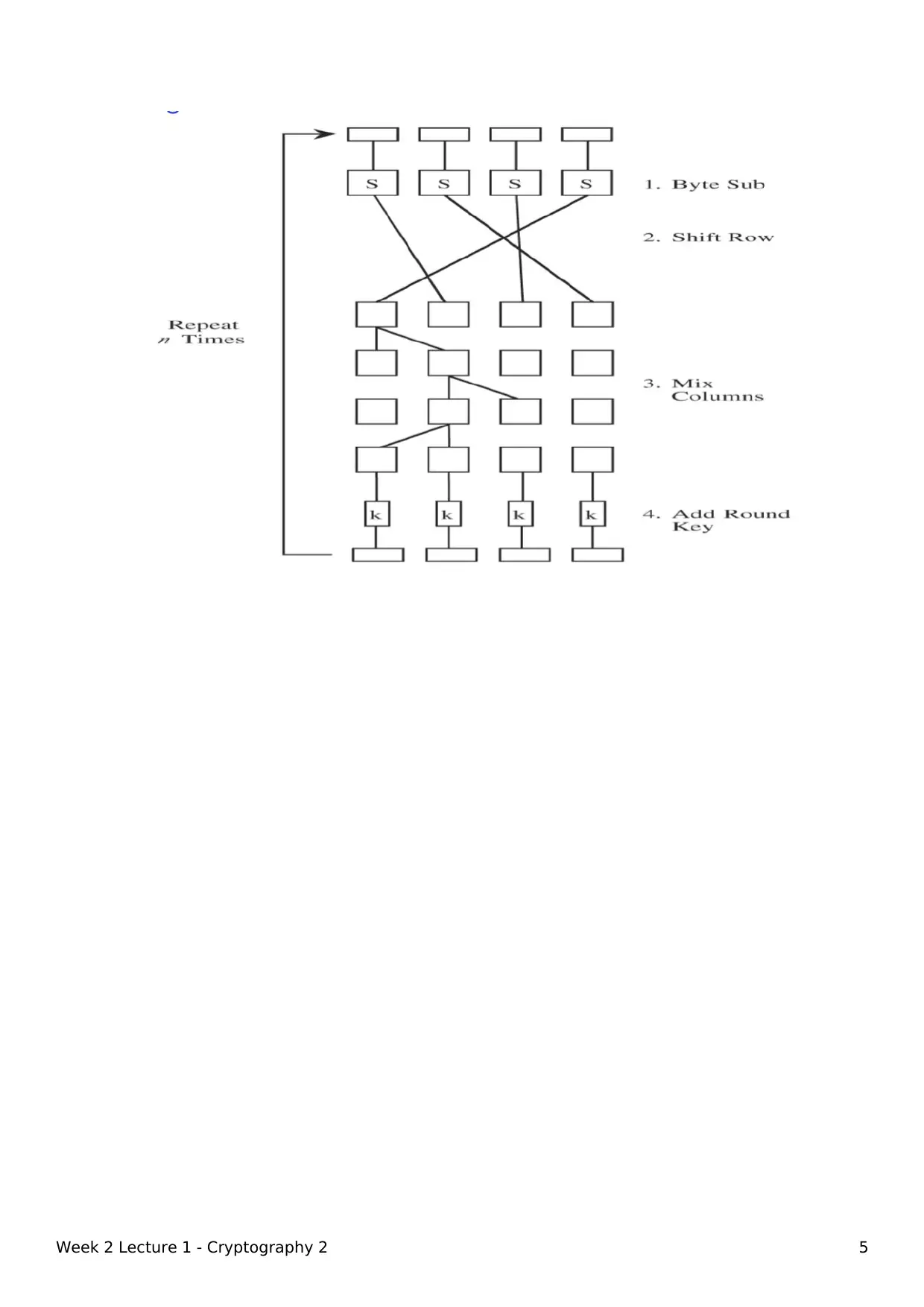
AES
AES uses repeat cycles of transposition and substitution on 128 bits blocks
and chaining the result.
Each cycle 10, 12 or 14 includes: 
byte substitution
shift row (transposition of row n+1 shifted left n Bytes)
mix column (exclusive OR bit)
add subkey: part of the key is exclusive ORd with cycle result.

Week 2 Lecture 1 - Cryptography 2 5