Solved System Identification and Adaptive Control Assignment

This assignment solution covers several key concepts in system identification and adaptive control. It includes the application of the instrumental variable approach to estimate parameters in a discrete-time system, analysis and optimization using the steepest descent algorithm for a parallel path system, and implementation of the recursive least squares algorithm for system identification with noisy signals. MATLAB code and plots are provided to illustrate the methods and results, offering a comprehensive understanding of these techniques in signal processing and control systems. Desklib provides students access to a wealth of solved assignments and study resources to aid in their academic pursuits.

Question 1:
Given, difference equation is
y(k) – 1.5y(k-1) + 0.7y(k-2) = u(k-1)
The measurement signal is ym(k) = y(k) + e(k)
The signal u(k) is the random binary signal and e(k) is the white noise signal with variance
4.0 and mean 9.0.
The signal is created in MATLAB as shown below.
MATLAB code:
function siggen
u = randi([0 1],400,1);
y(1) = u(1); y(2) = 1.5*y(1) + u(2);
for k=3:length(u)
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1);
end
y = y';
noise = sqrt(4)*randn(400,1);
for k=1:length(y)
ym(k) = y(k) + noise(k);
end
stem(y)

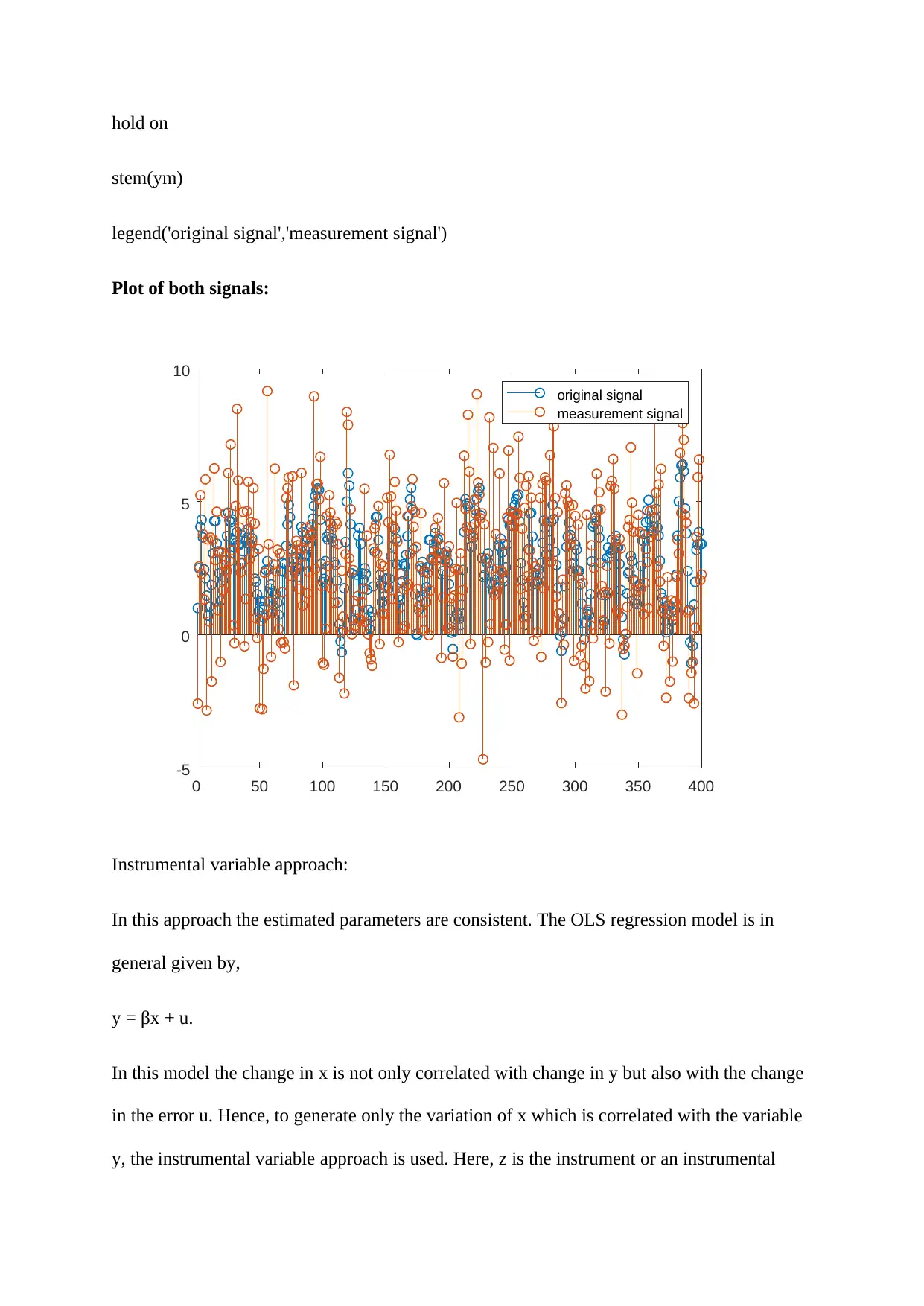
hold on
stem(ym)
legend('original signal','measurement signal')
Plot of both signals:
-5
0
5
10
0 50 100 150 200 250 300 350 400
original signal
measurement signal
Instrumental variable approach:
In this approach the estimated parameters are consistent. The OLS regression model is in
general given by,
y = βx + u.
In this model the change in x is not only correlated with change in y but also with the change
in the error u. Hence, to generate only the variation of x which is correlated with the variable
y, the instrumental variable approach is used. Here, z is the instrument or an instrumental

variable for the regressor variable x presenting the scalar regression model y = βx + u. Here, z
is not correlated with the u and correlated with x.
Now, the covariance matrix is given by,
P = 1/¿
Now, in the instrumental variable approach the cost function is given by,
Cost function J = (½)*(1/N)∑ ( y−∅ T ^θ¿)2 ¿
dJ/d θ = 0 => ∑ ( y−∅ T ^θ¿)¿ = 0.
Now, the instrumental variable approach is done using the ivar function in MATLAB for the
given discrete sequence data.
MATLAB function:
u = randi([0 1],400,1);
y(1) = u(1); y(2) = 1.5*y(1) + u(2);
for k=3:length(u)
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1);
end
y = y';
noise = sqrt(4)*randn(400,1);
for k=1:length(y)
ym(k) = y(k) + noise(k);
end

Output:
sys =
Discrete-time AR model: A(z)y(t) = e(t)
A(z) = 1 - 0.947 z^-1
Sample time: 1 seconds
Parameterization:
Polynomial orders: na=1
Number of free coefficients: 1
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using IVAR on time domain data "yhash".
Fit to estimation data: -17.85% ( focus)
FPE: 8.527, MSE: 8.442
Question 2:
In the given system the input x(n) is a white noise process having mean 0 and standard
deviation 1.
The system is a parallel path system and hence the output of the system is given by,
x ( n ) ( 0.2
z−0.8 – b
z−a )=o ( n )(as v(n)=0)
 o (n)/ x(n)=0.2/( z −0.8) – b/(z −a)¿

Now, assuming a,b and n are positive the inverse z transform of the transfer function is
Z (−1 )
( 0.2
z−0.8 – b
z−a ) = 0.25*0.8^n – b*a^(n-1)
Now, Steepest descent algorithm is applied to find the minimum of the transfer function.
Here, the two variables are a and b and value of n=3 is assumed i.e. the second sequence
point is presumed.
Hence, the function to apply Steepest descent algorithm is f = 0.25*(0.8^3) – b*(a^2)
MATLAB code:
f = @(a,b) (0.25*(0.8^3) - b*(a^2));
dfda = @(a,b) (-2*a*b);
dfdb = @(a,b) (-a^2);
subplot 211
fcontour(f,[-5 5])
grid on
a0 = 0;b0 = 0;
hold on
plot(a0,b0,'o')
%%% Steepest descent method
s1 = -dfda(a0,b0);
s2 = -dfdb(a0,b0);
ad = @(d) a0 + d*s1;

bd = @(d) b0 + d*s2;
fd = @(d)f(ad(d),bd(d));
subplot 212
ezplot(fd)
grid on
dhash = fminsearch(fd,0);
a1 = ad(dhash);b1 = bd(dhash);
subplot 211
plot(a1,b1,'o')
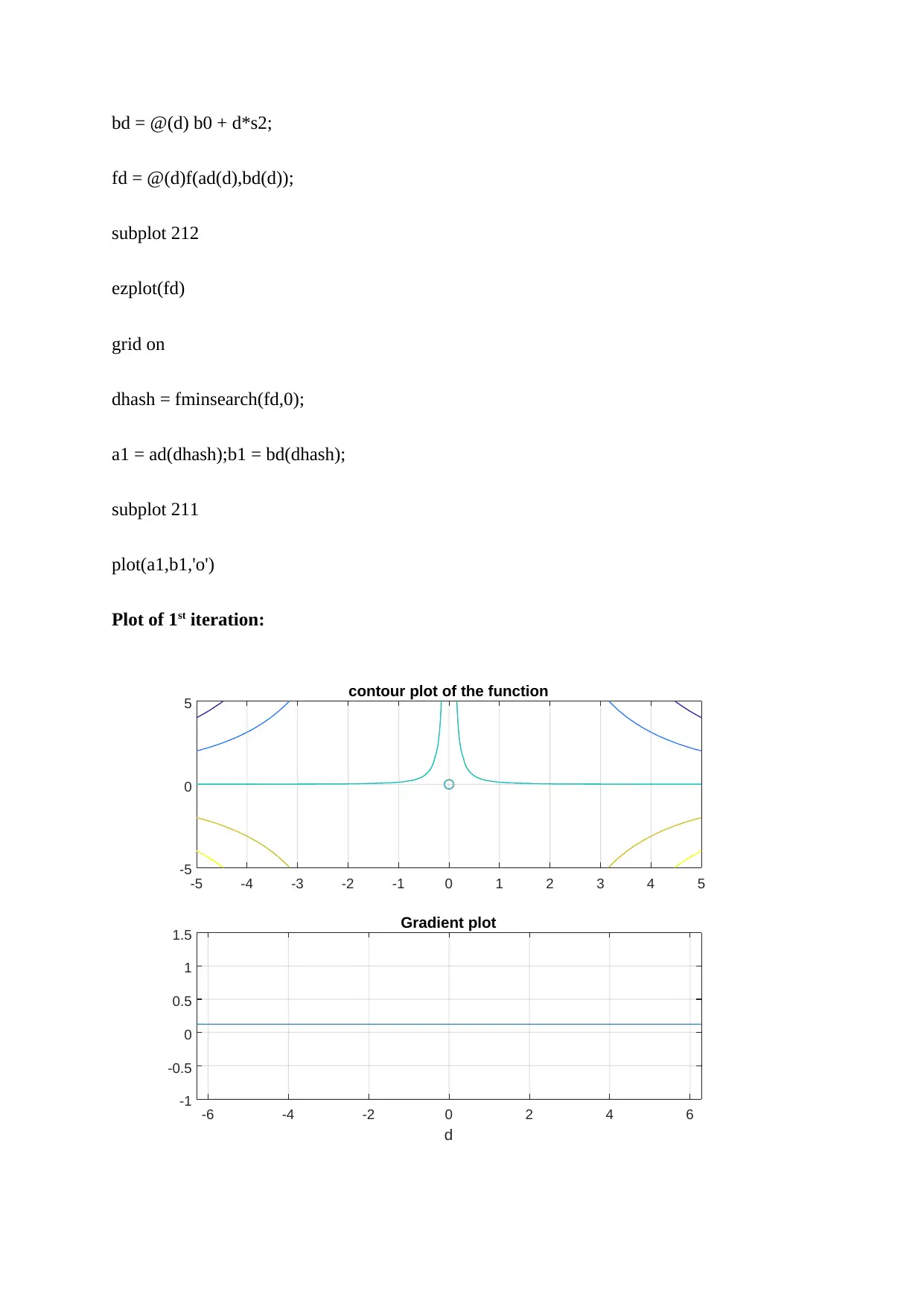
Plot of 1st iteration:
-5 -4 -3 -2 -1 0 1 2 3 4 5
-5
0
5 contour plot of the function
-6 -4 -2 0 2 4 6
d
-1
-0.5
0
0.5
1
1.5 Gradient plot

It can be seen that the gradient plot of the function at (0,0) is flat line. Hence, by steepest
descent method the minimum value of the function is at (0,0).
Question 3:
Given system is
y(k) – 1.5*y(k-1) + 0.7*y(k-2) = u(k-1) + e(k)
Here, e(k) is the white noise signal having variance 4.0 and u(k) is the random binary signal
having values ±1. The signal is simulated with N = 400 points.
MATLAB code:
val = [1 1];
index = randi(length(val),400,1);
u = val(index);
y(1) = u(1); y(2) = 1.5*y(1) + u(2);
for k=3:length(u)
y(k) = 1.5*y(k-1) - 0.7*y(k-2) + u(k-1);
end
e= sqrt(4)*randn(400,1);
for k=1:length(y)
y(k) = y(k) + e(k);
end
stem(y)

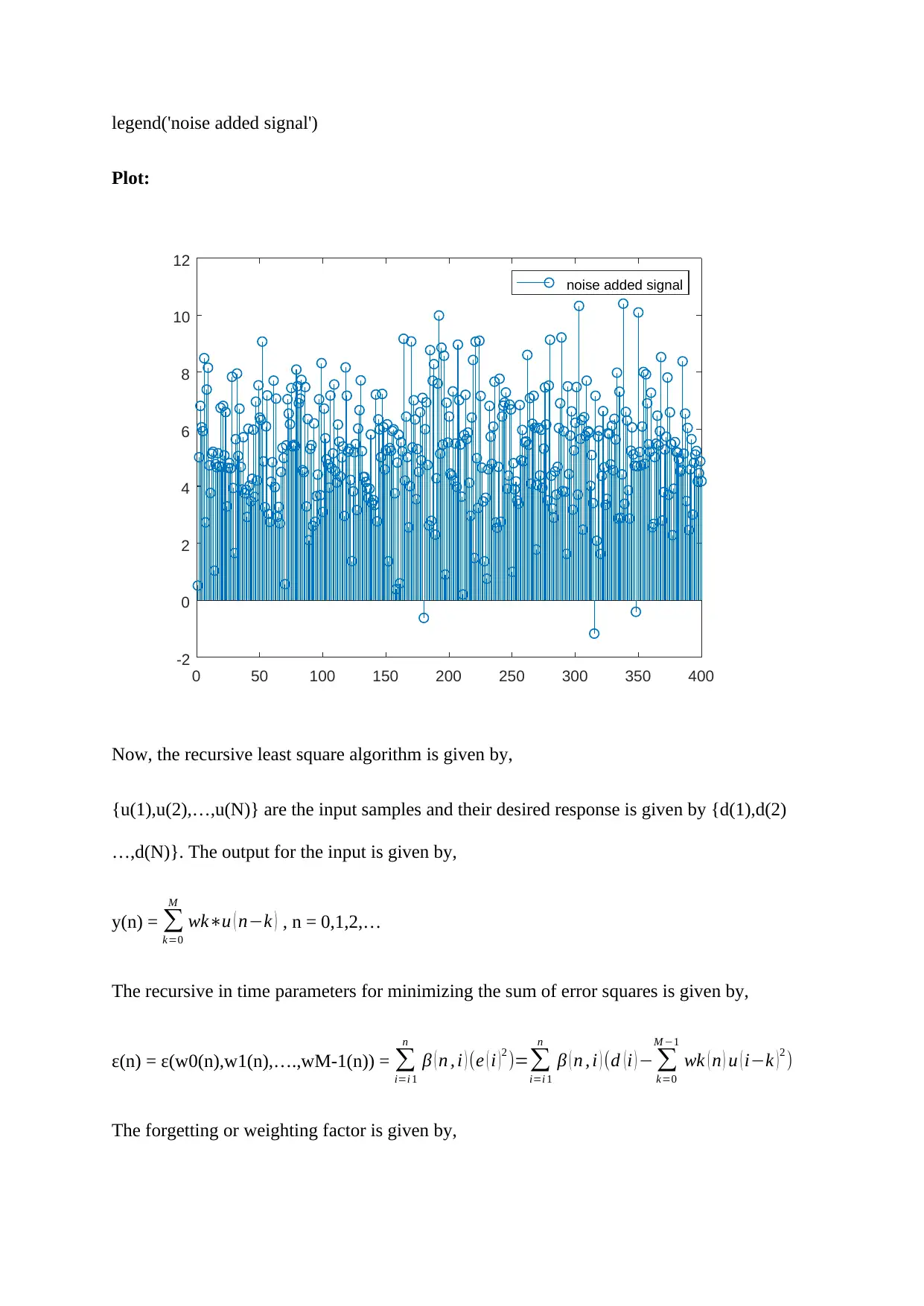
legend('noise added signal')
Plot:
-2
0
2
4
6
8
10
12
0 50 100 150 200 250 300 350 400
noise added signal
Now, the recursive least square algorithm is given by,
{u(1),u(2),…,u(N)} are the input samples and their desired response is given by {d(1),d(2)
…,d(N)}. The output for the input is given by,
y(n) = ∑
k=0
M
wk∗u ( n−k ) , n = 0,1,2,…
The recursive in time parameters for minimizing the sum of error squares is given by,
ε(n) = ε(w0(n),w1(n),….,wM-1(n)) = ∑
i=i 1
n
β ( n , i ) (e ( i )2 )=∑
i=i 1
n
β ( n , i ) (d (i ) − ∑
k=0
M −1
wk ( n ) u ( i−k )2 )
The forgetting or weighting factor is given by,

β ( n ,i ) = λn−i
Hence, the recursive least square in alternative way is given by,
θ ( k +1 ) =θ ( k ) +L ( k +1 ) [ y ( k +1 )−∅ T ( k +1 ) θ ( k )]
L(k+1) = P(k)/(λ+∅ T ( k +1 ) P(k )∅ (k +1)¿
P(k+1) = (1/ λ)( P ( k ) – P ( k ) ∅ ( k +1 ) ∅ T ( k +1 )
λ+∅ T ( k+1 ) P ( k ) ∅ ( k +1 ) )
The forgetting factor is given here as 0.95 and 1.
The cost function is given by
J = (1/N)( ∑
k =1
N
λN −k ( y ( k ) −∅ T ( k ) ^θ ) 2