Teaching Methods in Space and Geometry by Use of ICT - Report

This report delves into the application of Information and Communication Technology (ICT) in teaching space and geometry, focusing on secondary education. It explores various ICT tools, including Enhanced Subject Learning/Teaching by use of ICT (ESTUICT), and emphasizes the importance of understanding geometrical concepts. The study covers key areas such as spatial awareness, visualization, and problem-solving, aligning with the Van Hiele levels of geometric thinking. It details a two-week sequence of activities, incorporating assessment for learning techniques, and provides justifications based on developmental frameworks and the Van Hiele Teaching Phases. The report includes lesson plans, diagrams, and references to support the effective integration of ICT in mathematics education and is contributed by a student to be published on the website Desklib, a platform providing AI-based study tools for students.

Teaching Methods in Space and Geometry
Student’s Name
Affiliation
(Word Count)

Teaching Methods in Space and Geometry by use of ICT
Introduction
Teaching in mathematics has been improved through ICT in support of the teaching of the learners in
secondary. The study focuses on learning Geometry by using ICT as a way of incorporating the students to
understand the subject better and improved performance (Green & Parkin, 2014). Various forms of ICT that are
used for teaching mathematics include Enhanced Subject Learning/Teaching by use of ICT (ESTUICT). This
form makes use of internet resources, face to face teaching and makes use of emails. The teaching knowledge
for mathematics requires mastering of fundamental trajectories for proper acquisition of the teaching

framework. There are four outlines for developing geometrical learning such as student’s knowledge in
mathematics, instructional knowledge, interactions and knowledge on the content (Mason, 2009).
The teaching aspects to be covered include; introduction to Geometry, the lines, and angles, covering the
area of the triangles, area of quadrilaterals, special geometry relations, surface area and volumes of the triangles.
The aim of this study includes covering special space and geometry features for learning. Covering Geometry
requires planned learning in order to achieve the objectives of the study. The teacher is required to cover the
following areas in order to impart the mathematical skill to the learners (Pepin et al., 2014). The areas to be
covered v include; creating spatial awareness, visualizing abilities, wide experience in (2-3) dimensional
Geometry, applications on properties of geometry in mathematics, developing deductive understanding of the
subject to the learners, application of problem solving by use of ICT, and develop a positive attitude on the
students towards learning mathematics (Kuzniak & Rauscher, 2011).
Justification
The van Hiele’s Level of Geometric Thinking
The justification for teaching geometry includes the use of Van Hiele’s thinking that was established in
the school curriculum for the purpose of the teachers. The development of Geometry entails teachers with
detailed information on practice areas in mathematics. The justification remains on the basis of the applications
in space Geometry. Despite, the development in the space geometry it is important for the teachers to put more
emphasizes on the instructions provided for the students regarding mathematical concepts (Mardis 7 Everhart,
2013). However, the student does not think to a deductive level hence the need for the teachers to develop
various constructive relations with appropriate e approach to help the learners in thinking. Arguably, Van
Hiele’s theory is a justification of the learner’s way of thinking right from the tender age to adult level in terms
of academic performance (Gu, Wu & Xu, 2015).

Van Hiele focuses only three levels for covering normal school learning in various fields concerning
mathematics. The main projection includes the use of two dimensions and three-dimensional shapes. The first
level begins with a non-verbal method of thinking where the students are able to identify the shapes by their
own appearance (Mammona & Villani, 2012). The students will start by naming the shapes, for example, a
square, rectangle because the shape looks like a box. Also, the descriptive stage includes describing the shapes
and its component parts and students start by distinguishing various shapes. At this level, the learners develop a
language that enables them to perceive various properties in a logical way and start to understand for examp0le
the parts of the triangle by naming the sides (Lahrer & Chazan, 2012). In the last stage, the learners develop
informative deductions of various properties of the shapes in the order of logical arrangement. The students
learn on their own by use of the ICT integrated models and deduce how one concept precedes to another. This
justification includes the relationships, the theorems, and definitions of the formulae and understanding of the
course.
According to theory by Van Hiele’s, activities made to develop geometric thinking are simply a sequence of
five phases of different activities and types. They are made to promote the development of children thinking to
the different grades (Fujita, Jones & Kunimune, 2009). Similarly, there are different ways of using the phases
to plan lessons. Like for instance, a teacher might choose a square as a topic to deal with, therefore the teacher
has to prepare and design all the structure of a square and tasks. This might involve the manipulation also
constructing the square and also discussing the square through this method the children will be able to the
structure square and understand appropriately.
Phase one of the activities is about the inquiry. This states that learning always commences with a play, the
teacher should always encourage the children to interact with the materials freely and discover the most
important properties and structures of the square just to mention. Through this way the teacher is able to identify
the children thought and understanding. The second phase is about the direct orientation; this is where the
children are focused on the shapes of a structure. This as well would be observed when the children are playing.

They can notice the lengths of different sides of the shape, such as the equal sides and the non-equal. They can
also learn about the angles between the sides of the shapes and how they can be flipped to get a similar shape.
The third phase is about the explication where the children are able to play games to develop vocabulary, while
the fourth phase is about the free orientation, this is where the children engage in activities that open their minds
and perform different tasks.

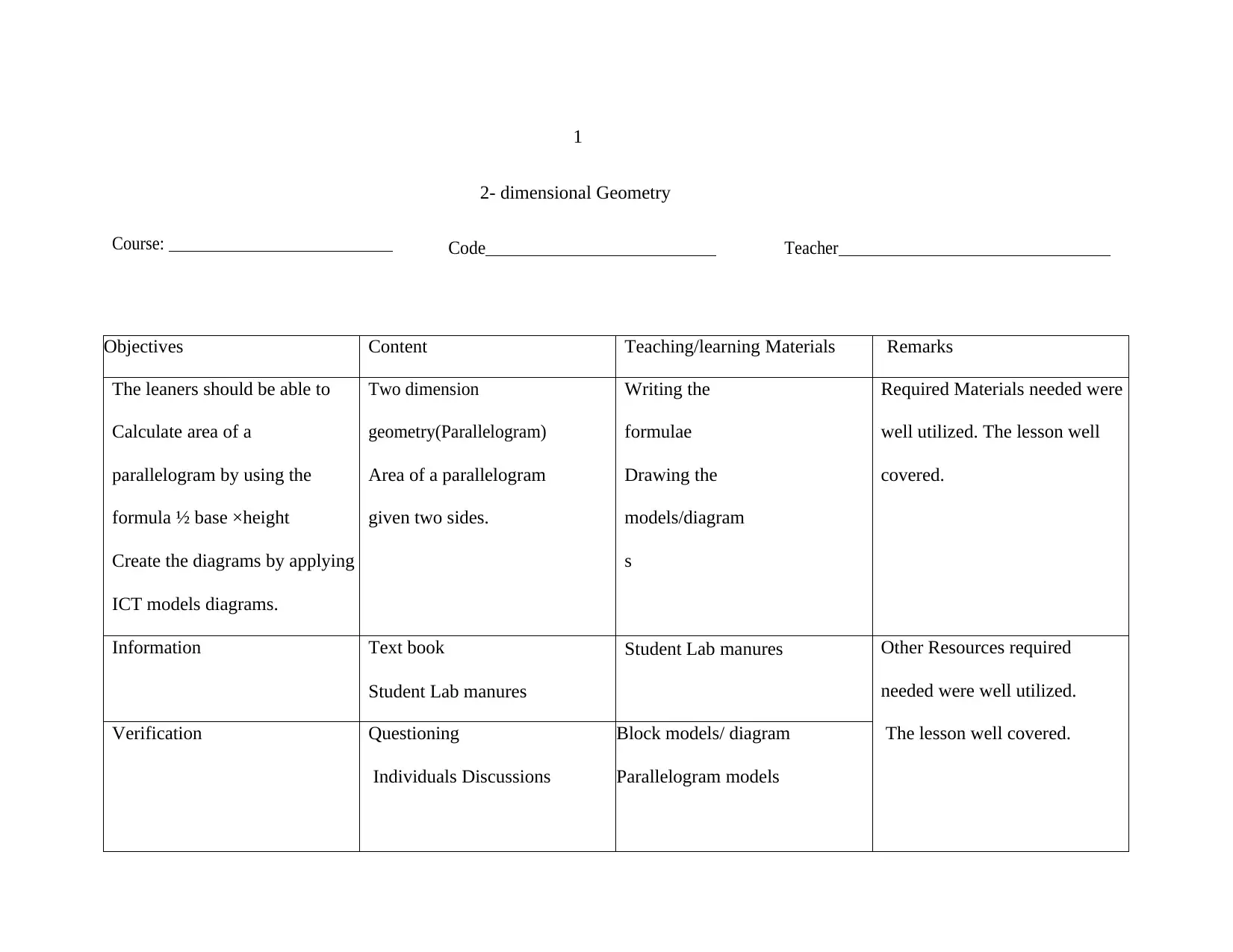
Course:
1
2- dimensional Geometry
Code Teacher
Objectives Content Teaching/learning Materials Remarks
The leaners should be able to
Calculate area of a
parallelogram by using the
formula ½ base ×height
Create the diagrams by applying
ICT models diagrams.
Two dimension
geometry(Parallelogram)
Area of a parallelogram
given two sides.
Writing the
formulae
Drawing the
models/diagram
s
Required Materials needed were
well utilized. The lesson well
covered.
Information Text book
Student Lab manures
Student Lab manures Other Resources required
needed were well utilized.
The lesson well covered.Verification Questioning
Individuals Discussions
Block models/ diagram
Parallelogram models

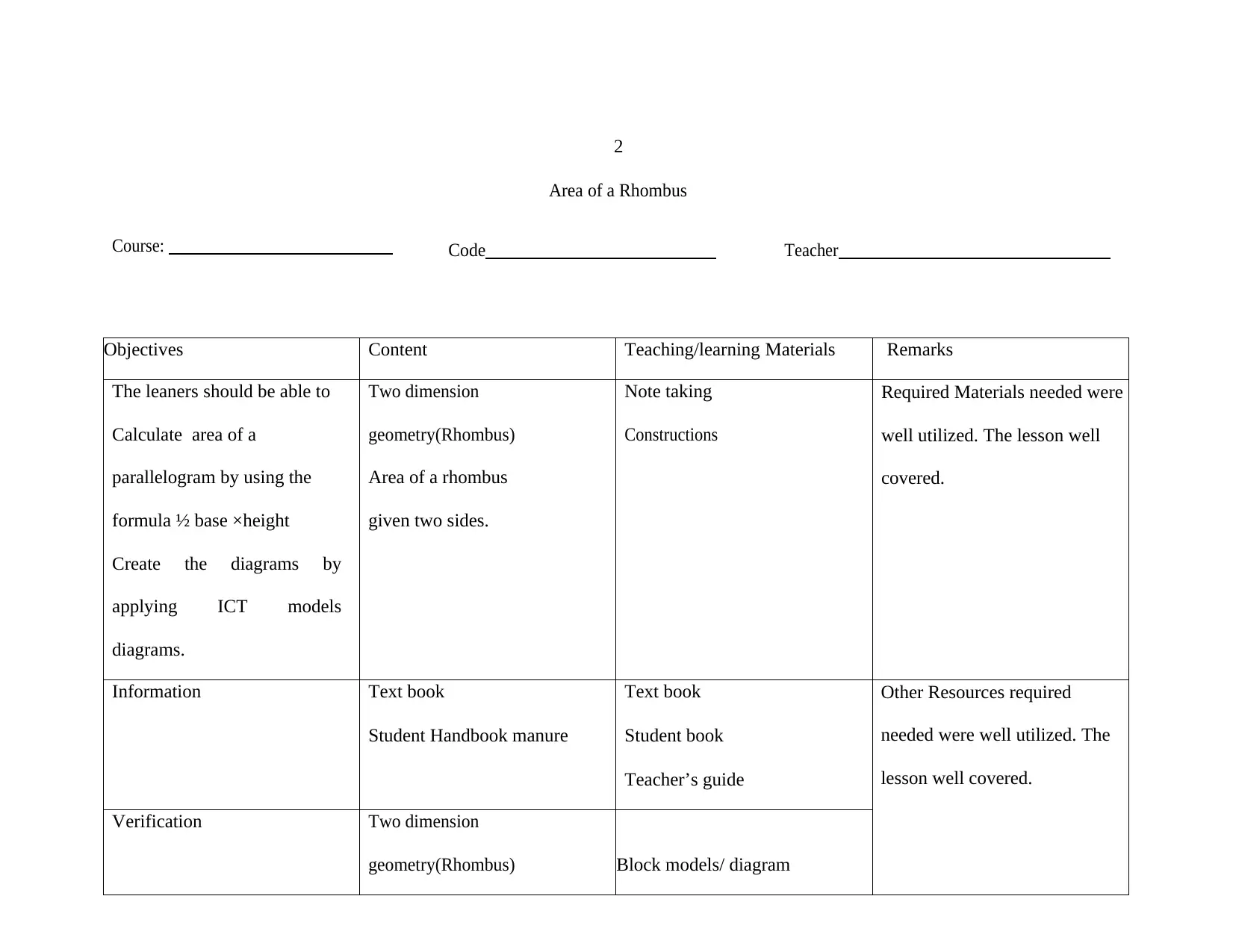
2
Area of a Rhombus
Course: Code Teacher
Objectives Content Teaching/learning Materials Remarks
The leaners should be able to
Calculate area of a
parallelogram by using the
formula ½ base ×height
Create the diagrams by
applying ICT models
diagrams.
Two dimension
geometry(Rhombus)
Area of a rhombus
given two sides.
Note taking
Constructions
Required Materials needed were
well utilized. The lesson well
covered.
Information Text book
Student Handbook manure
Text book
Student book
Teacher’s guide
Other Resources required
needed were well utilized. The
lesson well covered.
Verification Two dimension
geometry(Rhombus) Block models/ diagram

Area of a rhombus given two
sides.
Rhombus models

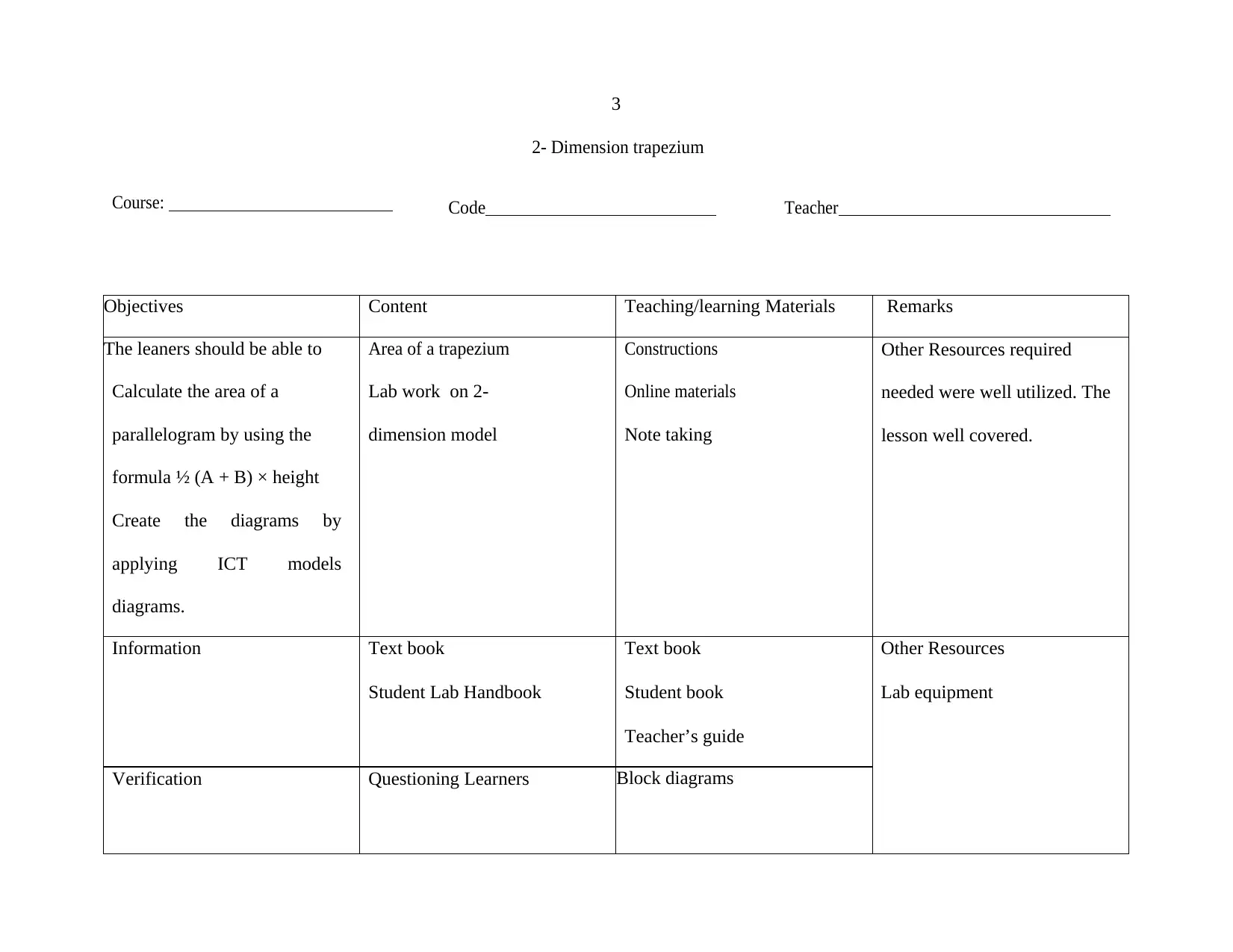
3
2- Dimension trapezium
Course: Code Teacher
Objectives Content Teaching/learning Materials Remarks
The leaners should be able to
Calculate the area of a
parallelogram by using the
formula ½ (A + B) × height
Create the diagrams by
applying ICT models
diagrams.
Area of a trapezium
Lab work on 2-
dimension model
Constructions
Online materials
Note taking
Other Resources required
needed were well utilized. The
lesson well covered.
Information Text book
Student Lab Handbook
Text book
Student book
Teacher’s guide
Other Resources
Lab equipment
Verification Questioning Learners Block diagrams

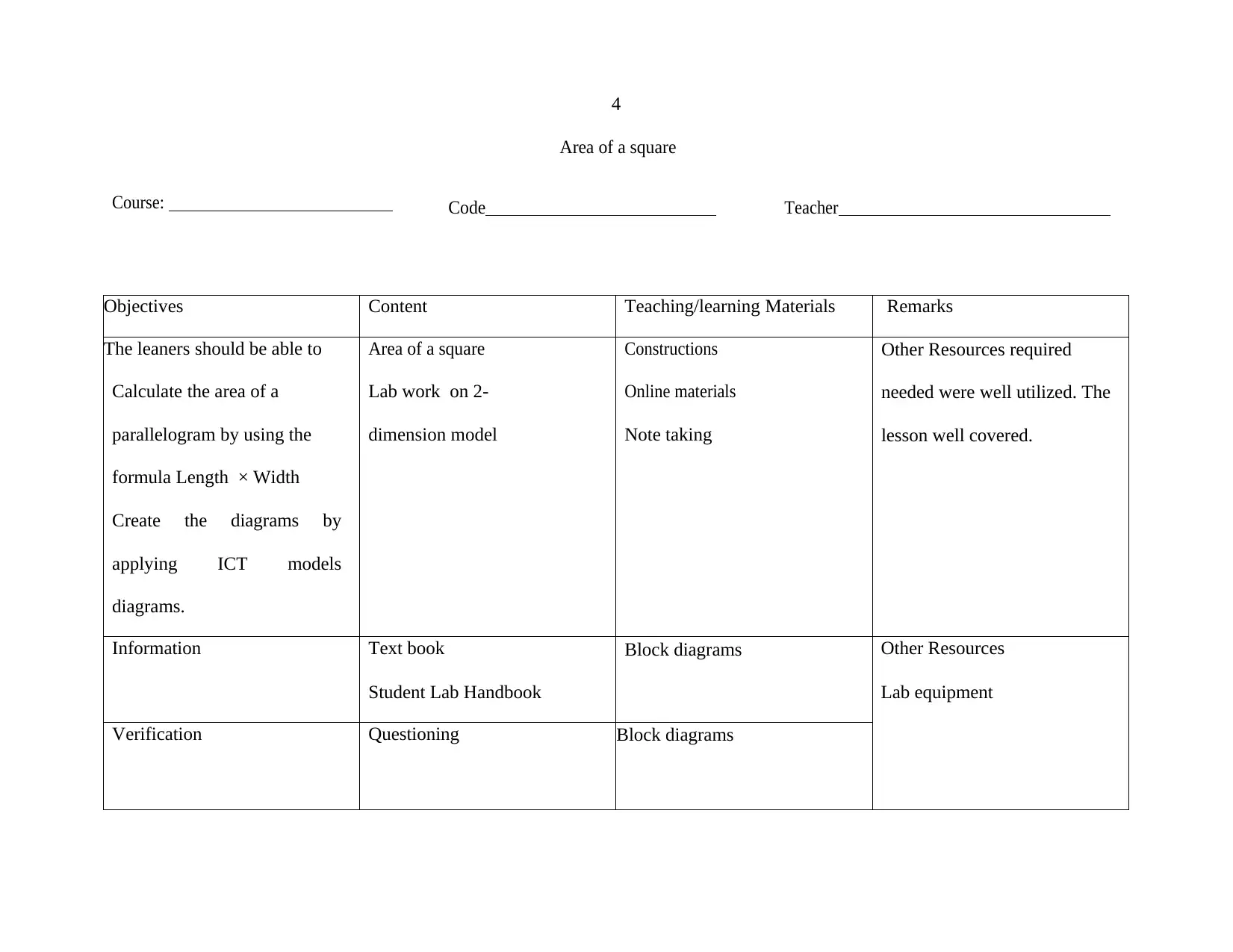
4
Area of a square
Course: Code Teacher
Objectives Content Teaching/learning Materials Remarks
The leaners should be able to
Calculate the area of a
parallelogram by using the
formula Length × Width
Create the diagrams by
applying ICT models
diagrams.
Area of a square
Lab work on 2-
dimension model
Constructions
Online materials
Note taking
Other Resources required
needed were well utilized. The
lesson well covered.
Information Text book
Student Lab Handbook
Block diagrams Other Resources
Lab equipment
Verification Questioning Block diagrams

5
Area of a Triangle Given the base and height
Course: Code Teacher
Objectives Content Teaching/learning Materials Remarks
The leaners should be able to
Calculate the area of a
parallelogram by using the
formula A= ½ base × height
Create the diagrams by
applying ICT models
diagrams.
Area of Triangle
Lab work on 2-
dimension model
Constructions
Online materials
Note taking
Other Resources required
needed were well utilized. The
lesson well covered.
Information Text book
Student Lab Handbook
Text book
Student math’s ,manure
Other Resources
Lab equipment
Verification Questioning Block diagrams

6
Area of a Triangle using 1/2absin α
Course: Code Teacher
Objectives Content Teaching/learning Materials Remarks
The leaners should be able to
Calculate the area of a
parallelogram by using the
formula A= ½ ABsin❑
Create the diagrams by applying
ICT models diagrams.
Area of a triangle given
two sides and included
angle
Lab work on 2-
dimension model
Constructions
Online materials
Note taking
Other Resources required
needed were well utilized. The
lesson well covered.
Information Text book
Student Lab Handbook
Text book
Student Lab Handbook
Other Resources
Lab equipment
Verification Questioning Block diagrams