Teesside University: TMA 3 - Complex Waveforms & Transients

This document presents solutions to an assignment focusing on complex waveforms and transients in R-L-C circuits. It covers topics such as even and odd functions, Fourier analysis, half-wave symmetry, and periodic waveforms. The solutions include mathematical expressions and waveform diagrams to illustrate key concepts. Furthermore, the assignment delves into power dissipation in a bulb, single-pulse waveforms, and total harmonic distortion (THD) calculations. Laplace transforms and inverse Laplace transforms are applied to solve circuit problems, and the transient response of a voltage source is analyzed. Desklib offers this assignment as a study resource, providing students access to past papers and solved problems.

Q1a)
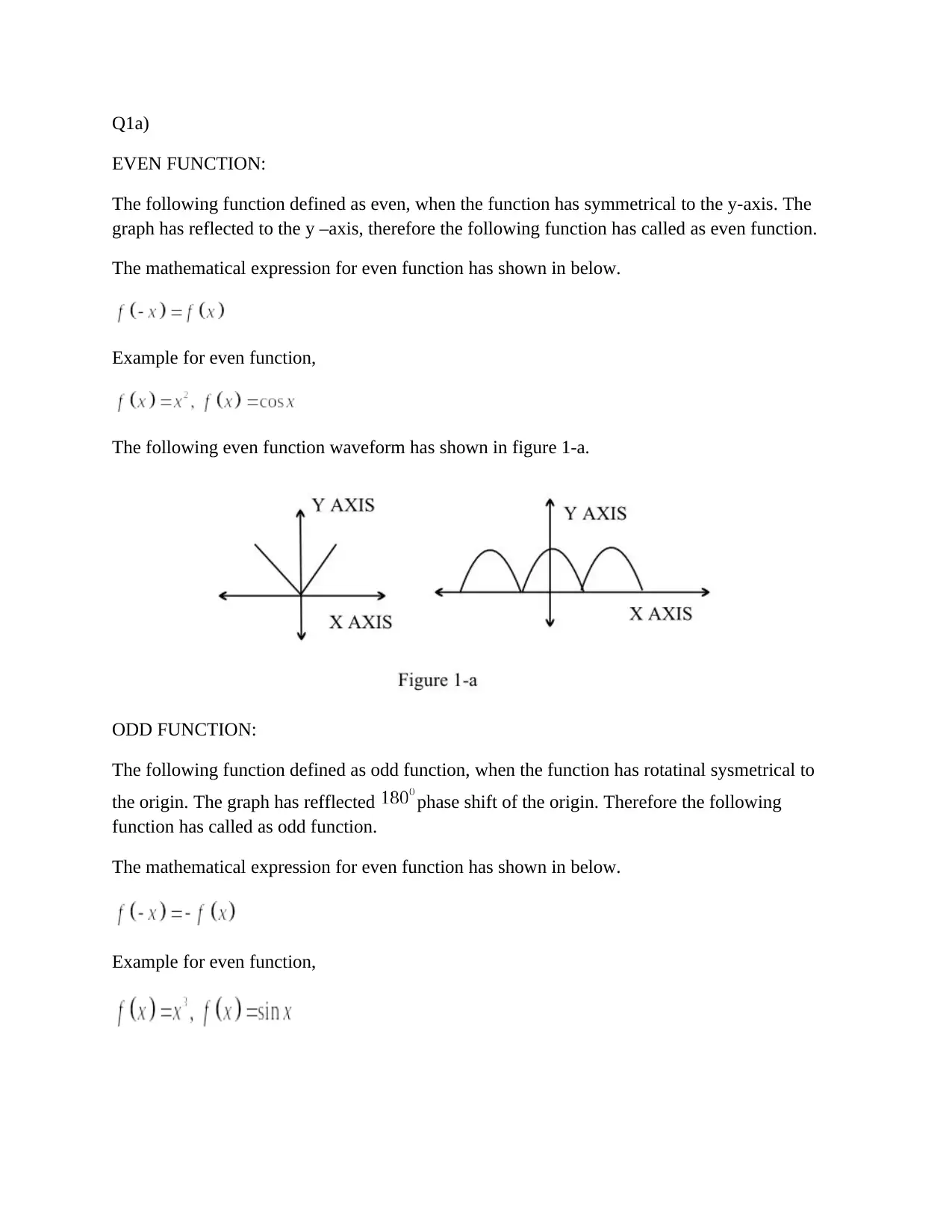
EVEN FUNCTION:
The following function defined as even, when the function has symmetrical to the y-axis. The
graph has reflected to the y –axis, therefore the following function has called as even function.
The mathematical expression for even function has shown in below.
Example for even function,
The following even function waveform has shown in figure 1-a.
ODD FUNCTION:
The following function defined as odd function, when the function has rotatinal sysmetrical to
the origin. The graph has refflected phase shift of the origin. Therefore the following
function has called as odd function.
The mathematical expression for even function has shown in below.
Example for even function,

The following odd function waveform has shown in figure 1-b.
Consider the fourier analysis,
If is odd or even function has shown in mathematical expression.
Consider the following even function,
Consider the following odd function.

2
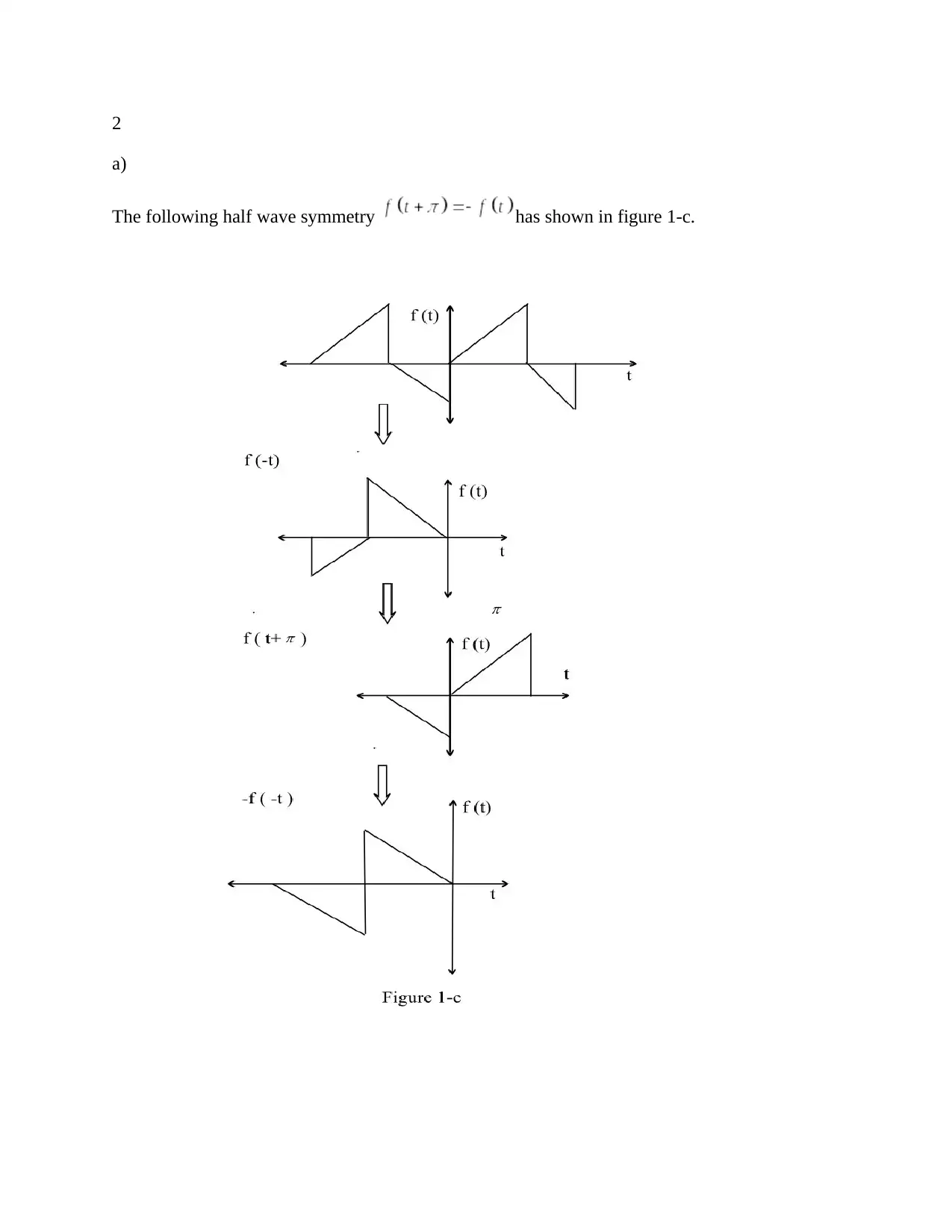
a)
The following half wave symmetry has shown in figure 1-c.

b)
The following periodic waveform has shown in figure 1,
Consider the Fourier series at t=0.
EVEN SYMMETRY EXPANSION:
The Fourier series does not contain sinusoidal term.
ODD SYMMETRY
The following Fourier series expansion contains sin term.
Consider the half wave symmetry.
Consider, the time shifting property.
The above relationship has satisfied when n=odd integer.
Therefore
The Fourier series expansion of the following half wave symmetry signal contains only odd
harmonics.
EVEN HALF WAVE SYMMETRIC:
When, DC=0
The signal contains odd harmonics and cos terms.

The following half symmetric wave form has shown in figure 2-a.
The following signal shifting t0 value , the signal become half wave symmetric signal.
Now signal became odd signal.
Therefore odd + half wave symmetric
Hence, the following Fourier series signal contain DC and sin term and odd harmonics.
SIGNAL-2
In this case DC gain is zero, therefore area under the waveform is zero.
This signal has even symmetriv. It contain COS terms with odd harmonics
SIGNAL-3
In this case DC gain is zero, therefore area under the waveform is zero.
SIN terms with odd harmonics.
SIGNAL-4
In this case DC gain is zero, therefore area under the waveform is zero.
COS terms with odd harmonics.
SIGNAL-5
In this case DC gain is zero, therefore area under the waveform is zero.
COS terms with odd harmonics.
SIGNAL-6
In this case DC gain is zero, therefore area under the waveform is zero.
COS terms with odd harmonics

QUESTOION 2:
a)
Determine the power dissipation in BULB.
The following data has given below.
Consider the following equation.
Therefore single phase AC voltage control with resistive load,
Give data.
Consider the equation 1, we get.
We know that,

Calculate the power dissipation in
b)
The following single pulse waveform where pulse width in and symmetrical about and
are given by
The following wave form has shown in (figure 1). It is always that is controlled rectification is
drift of the firing angle at half cycle. It has effect on wave form is symmetrical. Therefore the
circuit has contained fundamental component with harmonics present in the wave form.
The following waveform contains that fundamental with an odd harmonics and it can eliminate
with and odd harmonics and it can eliminate by using filter circuit. This device can increases
reliability of controlled rectifier.
c)
The following waveform has shown in figure 1a.

We know that.
Determine the .
Determine the .

Hence, we obtained the Fourier series.
Question3
c)
The following waveform has total harmonic distortion THD.
The fundamental RMS current
The fundamental RMS current
The total harmonics distortion has shown in below.
Consider the corresponding frequency.

Consider the Frequency of the harmonics
The fifth harmonics current (RMS)
Therefore, we can calculate THD by taking
Determine the total harmonic distortion THD.
d)
The original waveform from its principal harmonics has drawn in below figure 1-a.

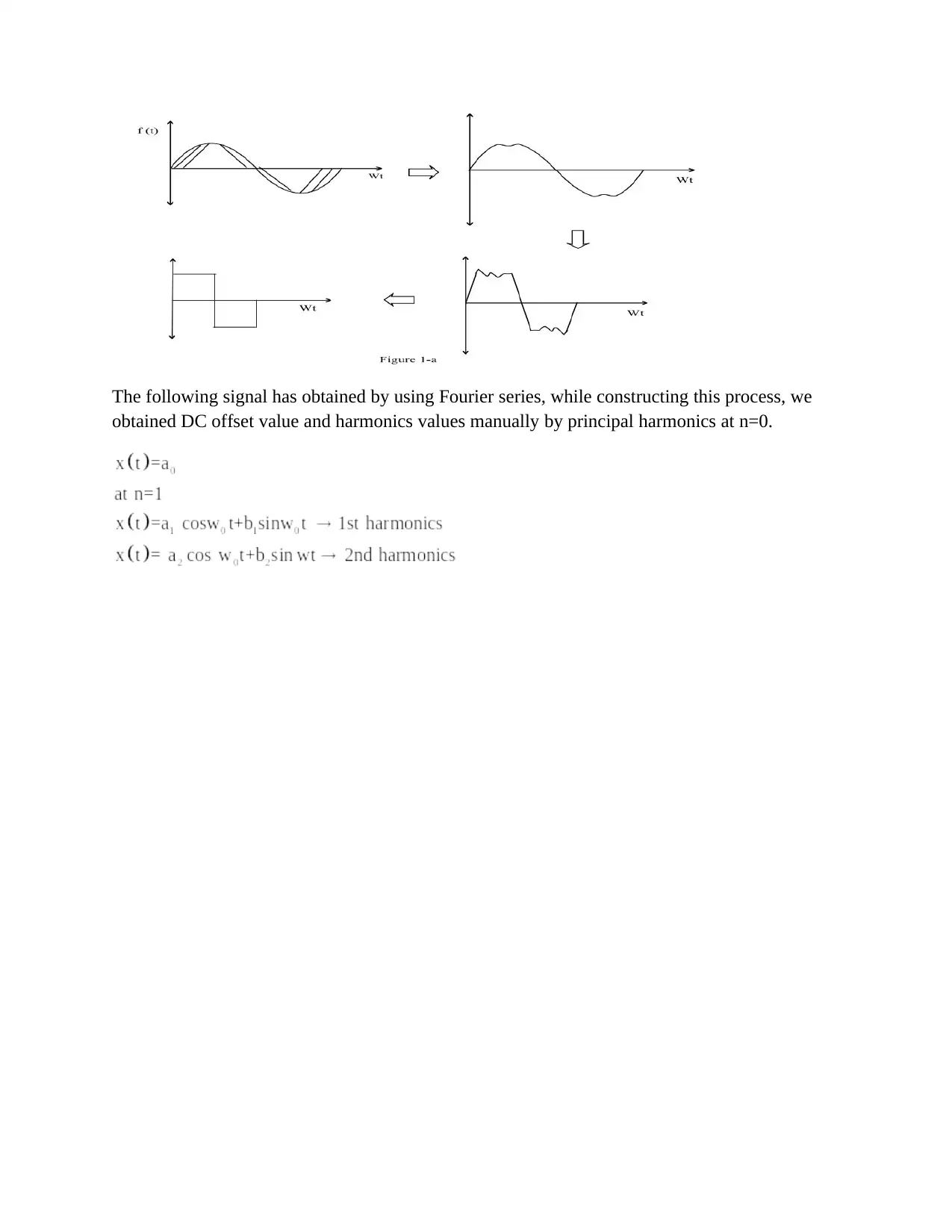
The following signal has obtained by using Fourier series, while constructing this process, we
obtained DC offset value and harmonics values manually by principal harmonics at n=0.

Q4
The following data has shown in below.
The following second order transfer function.
Consider the characteristic equation.
The transient response of the circuit has shown in axes waveform in figure 1-a.