Automata Theory Assignment: DFA and NFA Conversion, Solution

This document presents a solution to a Foundations of Computation assignment. The assignment focuses on constructing and converting finite automata. The solution includes the construction of deterministic finite automata (DFAs) for various languages, represented through diagrams. It also details the conversion of a non-deterministic finite automaton (NFA) into an equivalent DFA, with step-by-step working shown. The solution covers the epsilon-closure calculation, state transitions, and the construction of the DFA diagram. The document concludes with a bibliography of relevant sources.

Running head: FOUNDATIONS OF COMPUTATION
Foundations of Computation
Name of the Student
Name of the University
Author’s Note

1
FOUNDATIONS OF COMPUTATION
Answer to Question 1:
1. {w∈{a,b}∗|w has neither aa nor bb as a substring }{w∈{a,b}∗|w has neither aa nor bb as a
substring }
2. {w∈{a,b}∗|each a in w is immediately preceded by a b}{w∈{a,b}∗|each a in w is
immediately preceded by a b}
3. {w∈{a,b}∗|w has baba as a substring}{w∈{a,b}∗|w has baba as a substring}

2
FOUNDATIONS OF COMPUTATION
4. {w∈{a,b}∗|w has an odd number of a’s and an even number of b’s}{w∈{a,b}∗|w has an odd
number of a’s and an even number of b’s}
5. {w∈{a,b}∗|w has both ab and ba as substrings }{w∈{a,b}∗|w has both ab and ba as
substrings } Note: the string abaaba should be accepted.

3
FOUNDATIONS OF COMPUTATION
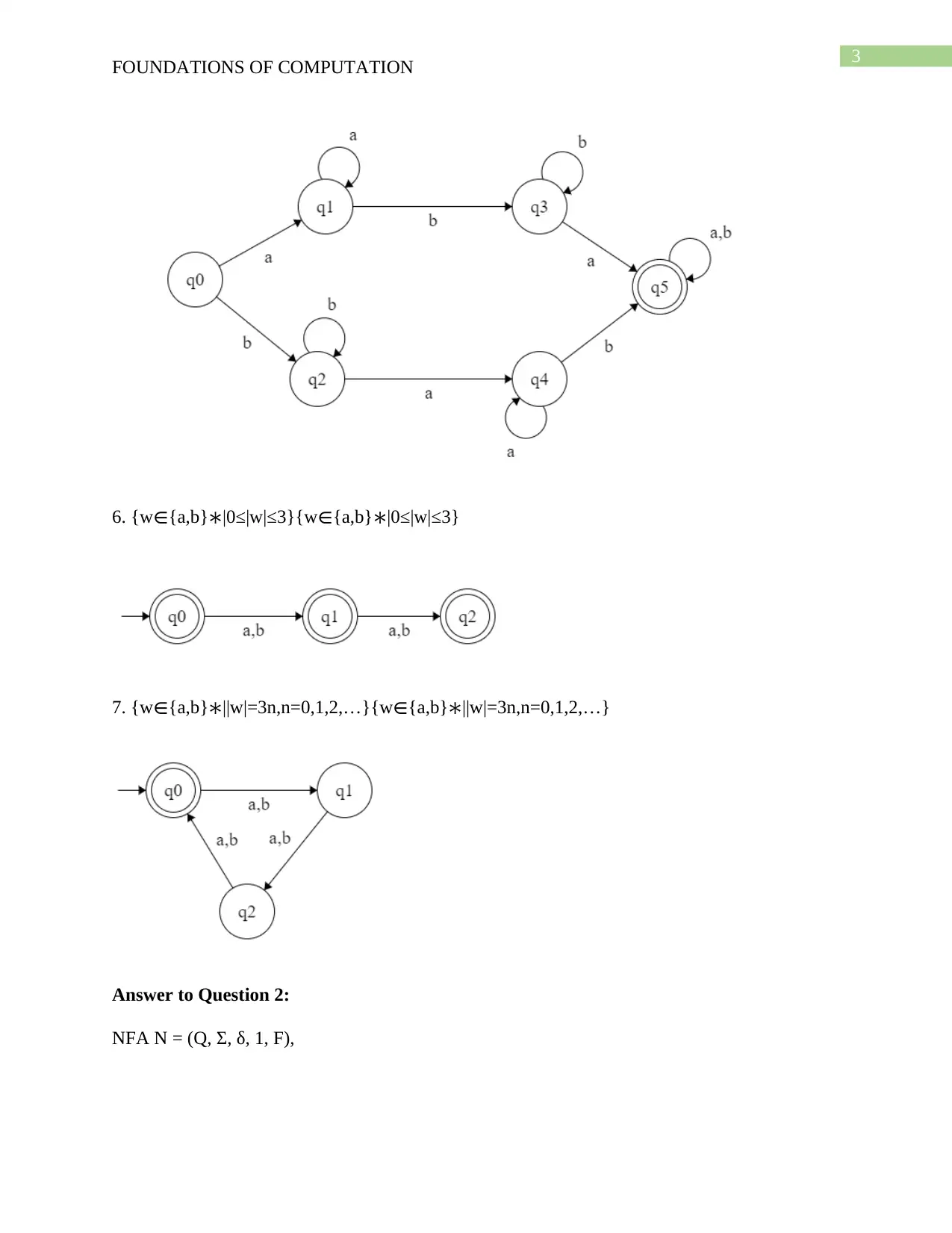
6. {w∈{a,b}∗|0≤|w|≤3}{w∈{a,b}∗|0≤|w|≤3}
7. {w∈{a,b}∗||w|=3n,n=0,1,2,…}{w∈{a,b}∗||w|=3n,n=0,1,2,…}
Answer to Question 2:
NFA N = (Q, Σ, δ, 1, F),

4
FOUNDATIONS OF COMPUTATION
where Q = {1, 2, 3}, Σ = {a, b}, 1 is the start state, F = {2}, and the transition function δ as in the
diagram of N. For constructing the DFA we consider M = (Q′ , Σ, δ′ , q′ 0 , F′) which is equal to
the NFA N1. The ε-closure is calculated for every subset of Q = {1, 2, 3}
Set R ⊆
Q
ε-closure E(R)
∅
{1}
{2}
{3}
{1, 2}
{1, 3}
{2, 3}
{1, 2, 3}
∅
{1, 2}
{2}
{3}
{1, 2}
{1, 2, 3}
{2, 3}
{1, 2, 3}
Then define Q′ = P(Q), so
Q ′ = { ∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }.
Thus, the start state for M is E({1}) = {1, 2}.
Set for accept states M is
F ′ = { {2}, {1, 2}, {2, 3}, {1, 2, 3} }
The transition of DFA M is shown in the below diagram:
1 Y Han & K Salomaa, Implementation and Application of Automata, in , Cham, Springer International Publishing,
2016.

5
FOUNDATIONS OF COMPUTATION
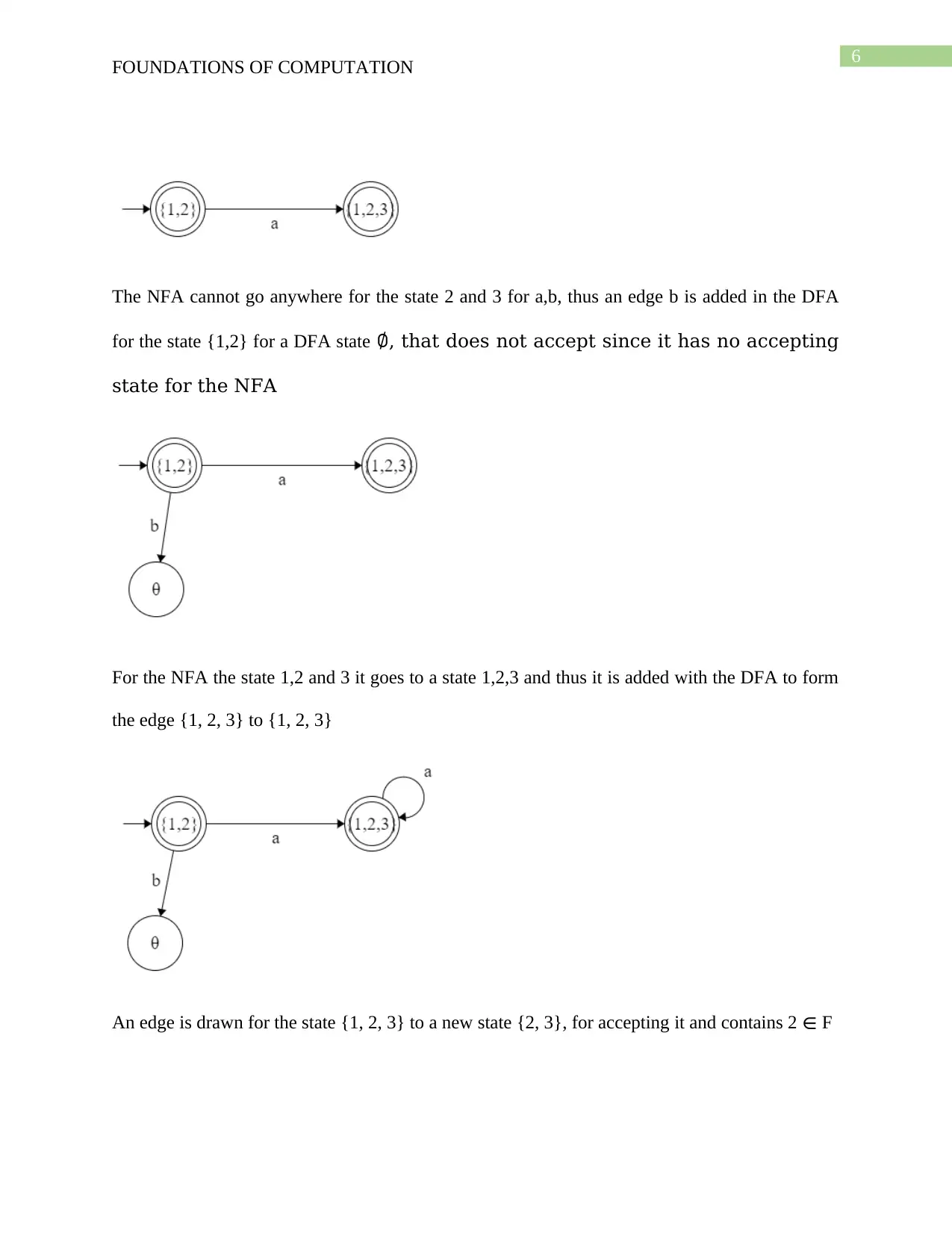
Some of the states are left out (e.g., {1}) in P(Q) in the diagram and DFA M for they are not
accessible for the state {1,2}.
An arc for the state ∅ is added and labelled with “a, b” such that the arc leaves for
corresponding each symbol in alphabet Σ, that is the requirement for a DFA.
A DFA for the state of set{1, 2} is given below:
The state {1, 2} is acts as an state of acceptance for the DFA since it has 2, that is accepting the
NFA.
For the DFA state {1,2} the NFA state can be 1,2 and 3 and the transition is drawn for the DFA
state {1,2} the new state is {1,2,3} that accepts the state for 2 ∈ F:

6
FOUNDATIONS OF COMPUTATION
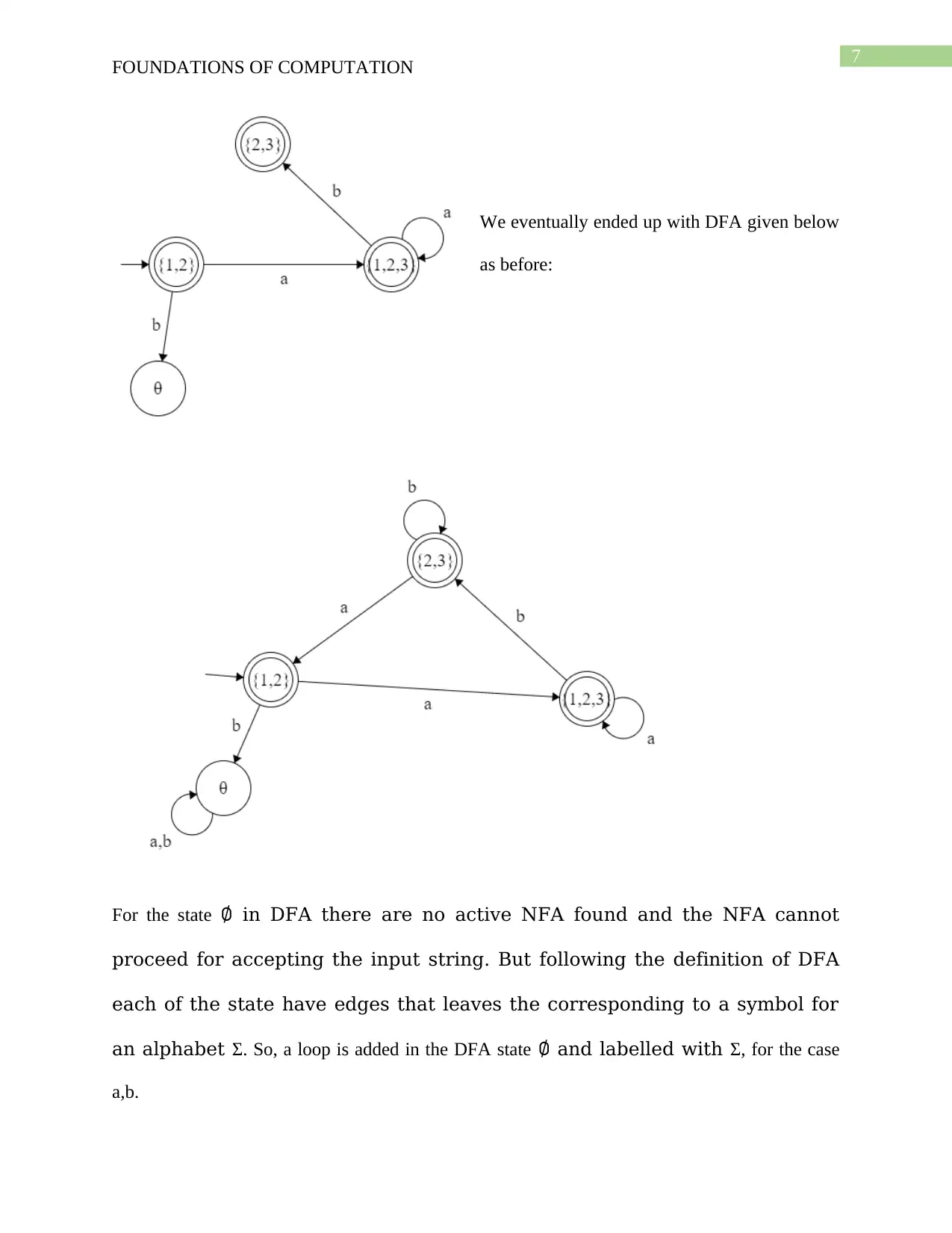
The NFA cannot go anywhere for the state 2 and 3 for a,b, thus an edge b is added in the DFA
for the state {1,2} for a DFA state ∅, that does not accept since it has no accepting
state for the NFA
For the NFA the state 1,2 and 3 it goes to a state 1,2,3 and thus it is added with the DFA to form
the edge {1, 2, 3} to {1, 2, 3}
An edge is drawn for the state {1, 2, 3} to a new state {2, 3}, for accepting it and contains 2 ∈ F

7
FOUNDATIONS OF COMPUTATION
We eventually ended up with DFA given below
as before:
For the state ∅ in DFA there are no active NFA found and the NFA cannot
proceed for accepting the input string. But following the definition of DFA
each of the state have edges that leaves the corresponding to a symbol for
an alphabet Σ. So, a loop is added in the DFA state ∅ and labelled with Σ, for the case
a,b.

8
FOUNDATIONS OF COMPUTATION