Analyzing Dynamics and Solutions in Theoretical Physics Models

The homework assignment involves a detailed exploration of several advanced concepts in theoretical physics. It starts by examining particle motion through the lens of Hamiltonian and Lagrangian mechanics, emphasizing energy conservation principles. The assignment further delves into solving heat equations with specific boundary conditions, leveraging Fourier series for convergence analysis. Additionally, it addresses electromagnetic field dynamics in special relativity contexts, using trial trajectories to explore gravitational effects. Key components include deriving solutions under various constraints and analyzing theoretical implications through Newtonian mechanics and Feynman's proposals. The comprehensive approach offers insights into the fundamental principles governing these physical systems.

Solution 1
a) As be definitions
L=KE−PE
L= 1
2 m ˙x1
2 + 1
2 m ˙x2
2− 1
2 K ( x1
2+ x2
2
)
Now momentum is
p1= ∂ L
∂ ˙x1
=m ˙x1
p2= ∂ L
∂ ˙x2
=m ˙x2
As
L= 1
2 m ˙xI ˙x J−e (φ− ˙xJ A j)
So
pi= ∂ L
∂ ˙xi
= ∂
∂ ˙xi ( 1
2 m ˙xI ˙xJ−e ( φ− ˙xJ A j ) )
pi= 1
2 m ˙¿ 2 xI −e (0−1∗A j)
pi=m ˙xi+e A j ¿
b) The conservation is
The second reads
pi=m ˙xi+ e Ai
d
dt pi= d
dt ( m ˙xi +e Ai ) =0
d
dt ( m ˙xi )=0
That x component of momentum is conserved.

c)
H= ˙x j
dL
d ˙x j
−L
L= 1
2 m ˙x j ˙x j−e (∅ − ˙x j A j)
So in
H= ˙x j
dL
d ˙x j
−L
H= ˙x j
d
d ˙x j ( 1
2 m ˙x j ˙x j−e ( ∅ − ˙x j A j ) )− ( 1
2 m ˙x j ˙x j −e ( ∅ − ˙x j A j ) )
H= ˙x j (m ˙x j− d
d ˙x j
e ( ∅ − ˙x j A j ) )−( 1
2 m ˙x j ˙x j−e ( ∅ − ˙x j A j ) )
H= ( p j− d
d ˙x j
e ( ∅ − ˙x j A j ) )−( 1
2 p j−e (∅ − ˙x j A j ))
H= ( 1
2 pj − d
d ˙x j
e ( ∅ − ˙x j A j )) + ( e ( ∅ − ˙x j A j ) )
H= ( 1
2 m ( p j−e A j )2+ e ∅ )
d)
H= ( 1
2 m ( p j−e A j )2+ e ∅ )
Now
H= ˙x j
dL
d ˙x j
−L
Also
p1= ∂ L
∂ ˙x1
=m ˙x1

H= ˙x j pi−mx
Hence
˙x j pi−mx=( 1
2 m ( p j−e A j )
2 +e ∅ )
˙x j pi−mx=( 1
2 m ( p j
2 +e2 A j
2−2 p j e A j )+e ∅ )
˙x j pi−mx=( 1
2 m ( p j
2 +e2 A j
2¿ )+e ∅ −− p j e A j
m )
˙x j pi−mx=( 1
2 m ( p j
2 +e2 A j
2¿ )+e ∅ −− p j e A j
m )
So on comparison
˙xi= 1
m ( pi −e Ai )
˙pi= e
m ( p j−e A j ) ∂ A j
∂ x j
−e ∂ ∅
∂ xi
e) As we can see that there should be balancing momentum for pz component of the system.
The subtraction of kinetic and potential energy is not conservative in z direction. Mainly
because of no balancing component available and hence this is not conservative.
f)
From
˙xi= 1
m ( pi −e Ai )
˙pi= e
m ( p j−e A j ) ∂ A j
∂ x j
−e ∂ ∅
∂ xi
Here
Bey=e Ai
So now

˙x= 1
m ( px+ Bey )
˙px=−Ee
˙py=−Be ˙x
˙y= py
m
g) Magic velocity
By law of conservation
1
2 B v2= 1
2 Ev
Bv=E
v= E
B
h) In case if E>cB
In this part we have higher component of em wave than velocity of light. This comes under
uncertainty.
This is physically not possible to have this condition.
Solution 2
a) Given
h ( t )= ∑
n=−∞
∞
f ( x +n )
now as we know that series converges to the point were summation and avering is given.
Using standard fourier formula, we can see period is 1.

b)
∂u
∂ t =2 ∂2 u
∂ x2
u ( 0 , t ) =u ( 5 ,t ) =0
u ( x , 0 )=f ( x )=−4 sin ( πx )+ 3sin ( 2 πx ) 0 ≤ x ≤ 5
Now
Now assuming
u( x , t)= X (x) T ( t)
Now
X ( x ) T ' ( t ) =2 X' ' ( x ) T ( t )
X' '( x )
X ( x ) =1
2
T ' ( t )
T ( t )
Now assuming the independency of both the sides we have below condition for any given
constant say K.
X' ' ( x )
X ( x ) =K
1
2
T ' ( t )
T ( t ) =K
So solution for above two variables given non zero K

X ( x ) =l1 e√ K x+l2 e− √ K x
T ( t )=l3 e2 Kt
Hence finally we have
u ( x , t )=X ( x ) T ( t )
u ( x , t ) =(l1 e √ K x+ l2 e− √ K x )l3 e2 Kt
c) Heat equation
Now for above equation when we apply boundary conditions
u ( x , t )= An sin ( nπ
L x )e−2 π 2 n2 t
L2
Here
An =−2i l1 l3
√ K= nπ
L i
Now heat equation satisfies the below equation
u ( x , t ) =∑
n=1
∞
An sin ( nπ
L x ) e−2 π 2 n2 t
L2
Considering

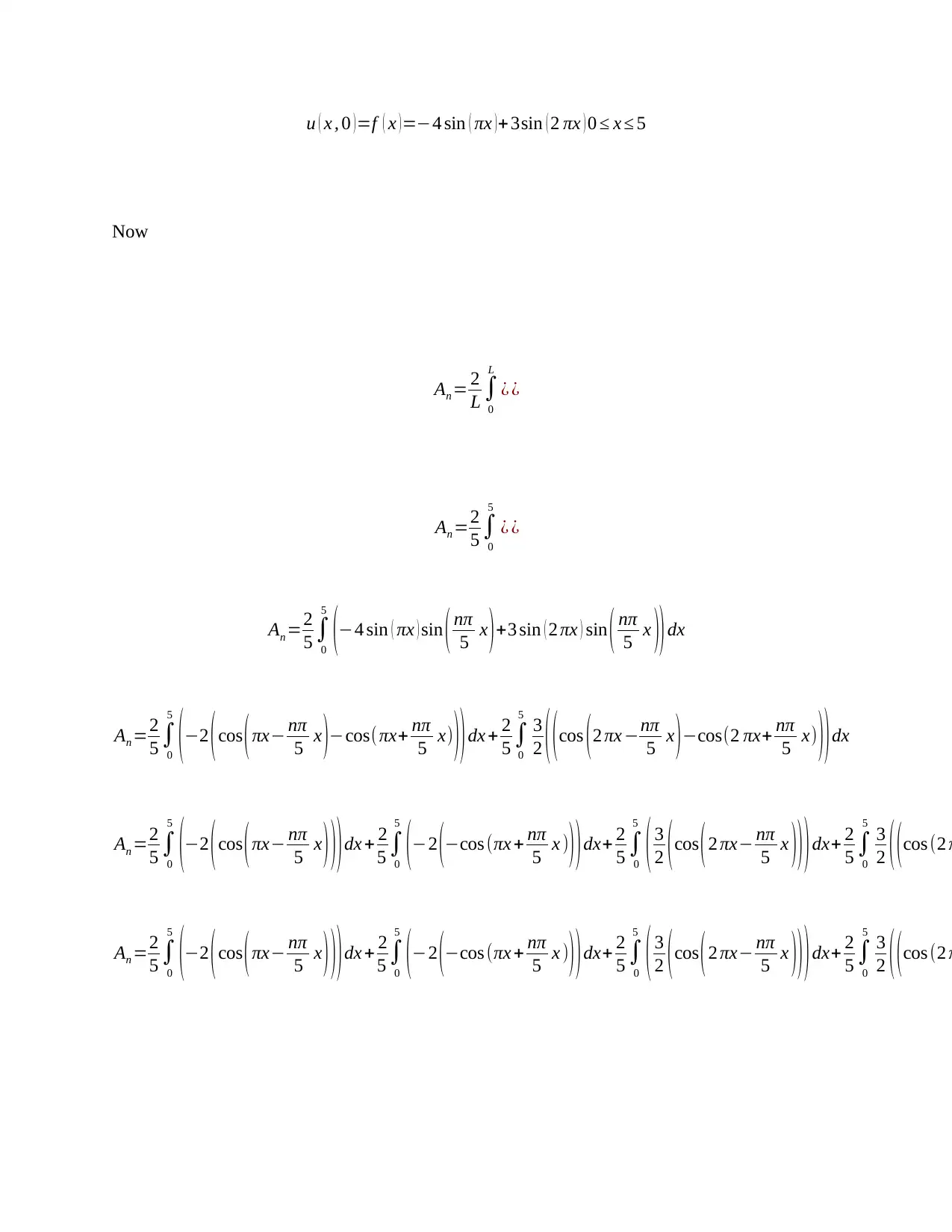
u ( x , 0 )=f ( x )=−4 sin ( πx )+ 3sin ( 2 πx ) 0 ≤ x ≤ 5
Now
An = 2
L ∫
0
L
¿ ¿
An =2
5 ∫
0
5
¿ ¿
An =2
5 ∫
0
5
(−4 sin ( πx ) sin ( nπ
5 x ) +3 sin ( 2 πx ) sin ( nπ
5 x )) dx
An =2
5 ∫
0
5
(−2 (cos (πx− nπ
5 x )−cos( πx+ nπ
5 x) ))dx + 2
5 ∫
0
5
3
2 ( (cos (2 πx −nπ
5 x )−cos(2 πx+ nπ
5 x) ))dx
An =2
5 ∫
0
5
(−2 ( cos ( πx− nπ
5 x ) )) dx + 2
5 ∫
0
5
(−2 (−cos (πx + nπ
5 x )) ) dx+ 2
5 ∫
0
5
( 3
2 ( cos ( 2 πx− nπ
5 x )) ) dx+ 2
5 ∫
0
5
3
2 ( ( cos (2 π
An =2
5 ∫
0
5
(−2 ( cos ( πx− nπ
5 x ) )) dx + 2
5 ∫
0
5
(−2 (−cos (πx + nπ
5 x )) ) dx+ 2
5 ∫
0
5
( 3
2 ( cos ( 2 πx− nπ
5 x )) ) dx+ 2
5 ∫
0
5
3
2 ( ( cos (2 π

An =2
5 [ (−2 (sin (πx− nπ
5 x ) ) )
π− nπ
5 ]0
5
+ 2
5 [ (−2 (sin (πx+ nπ
5 x ) ))
π + nπ
5 ]0
5
+ + 2
5 [ ( 3
2 (sin (2 πx− nπ
5 x )) )
2 π − nπ
5 ]0
5
+ +2
5 [ ( 3
2 (sin (2 πx + nπ
5 x
2 π + nπ
5
An =2
5 [ (−2 ( sin ( 5 π −nπ ) ) )
π − nπ
5 ]0
5
+ 2
5 [ (−2 ( sin (5 π +nπ ) ) )
π + nπ
5 ]0
5
+ +2
5 [ ( 3
2 ( sin ( 10 π−nπ ) ) )
2 π −nπ
5 ]0
5
+ +2
5 [ ( 3
2 ( sin ( 10 π −nπ ) ) )
2 π + nπ
5 ]0
5
An = (−2 ( sin (5 π−nπ ) ) )
π −nπ
5
+ (−2 ( sin ( 5 π + nπ ) ) )
π + nπ
5
+ ( 3
2 ( sin ( 10 π−nπ ) ))
2 π− nπ
5
+ ( 3
2 ( sin ( 10 π−nπ ) ) )
2 π + nπ
5
Hence we have
An = (−2 ( sin (5 π−nπ ) ) )
π −nπ
5
+ (−2 ( sin ( 5 π + nπ ) ) )
π + nπ
5
+ ( 3
2 ( sin ( 10 π−nπ ) ))
2 π− nπ
5
+ ( 3
2 ( sin ( 10 π−nπ ) ) )
2 π + nπ
5
u ( x , t ) =∑
n=1
∞
An sin ( nπ
L x ) e−2 π 2 n2 t
L2
d)

Now given
c=1 , L=2
f ( x ) = { x if 0 ≤ x ≤ 1
2− x if 1 ≤ x ≤2
Using previous question solution
u ( x , t ) =∑
n=1
∞
An sin ( nπ
L x ) e−2 π 2 n2 t
L2
An = 2
L ∫
0
L
f ( x ) sin ( nπ
L x )dx
We have using f(x)
An = 2
L ∫
0
L
f ( x ) sin ( nπ
L x )dx
An =
{ 2
L ∫
0
L
f ( x ) sin ( nπ
L x ) dx if 0 ≤ x ≤ 1
2
L ∫
0
L
f ( x ) sin ( nπ
L x ) dx if 1 ≤ x ≤ 2
Keeping f(x) values
An =
{ 2
L ∫
0
L
( x ) sin ( nπ
L x )dx if 0≤ x ≤ 1
2
L ∫
0
L
( 2−x ) sin ( nπ
L x )dx if 1 ≤ x ≤2

e)
Again based on constants
An =
{ 2
2∫
0
2
( x ) sin ( nπ
2 x )dx if 0≤ x ≤ 1
2
2 ∫
0
2
( 2−x ) sin ( nπ
2 x )dx if 1 ≤ x ≤ 2
An =
{ ∫
0
2
( x ) sin ( nπ
2 x ) dx if 0 ≤ x ≤1
∫
0
2
( 2−x ) sin ( nπ
2 x ) dx if 1≤ x ≤ 2
An =∫
0
2
( x ) sin ( nπ
2 x ) dx
An =x∫
0
2
sin ( nπ
2 x )dx + 1
nπ
2
∫
0
2
cos ( nπ
2 x )dx
An =−x
nπ
2
[ cos ( nπ
2 x ) ]0
2
+ 1
( nπ
2 )
2 [ sin ( nπ
2 x ) ]0
2
An =−x
nπ
2
( sin ( nπ ) −1 ) + sin ( nπ )
( nπ
2 ) 2

f)
An =∫
0
2
( 2 ) sin ( nπ
2 x ) dx−∫
0
2
( x ) sin ( nπ
2 x ) dx
An =∫
0
2
( 2 ) sin ( nπ
2 x )dx−
(x∫
0
2
sin ( nπ
2 x )dx + 1
nπ
2
∫
0
2
cos ( nπ
2 x )dx
)
An =2 [cos ( nπ
2 x ) ]0
2
−
(−x
nπ
2
[cos ( nπ
2 x ) ]0
2
+ 1
( nπ
2 )2 [sin ( nπ
2 x ) ]0
2
)
An =2 ( sin ( nπ ) −1 ) + x
nπ
2
( sin ( nπ ) −1 ) − sin ( nπ )
( nπ
2 )
2
Hence we have
An =
{ −x
nπ
2
( sin ( nπ )−1 ) + sin ( nπ )
( nπ
2 )2 if 0 ≤ x ≤ 1
2 ( sin ( nπ )−1 ) + x
nπ
2
( sin ( nπ )−1 ) −sin ( nπ )
( nπ
2 )2 if 1≤ x ≤ 2
Final solution is

u ( x , t ) =∑
n=1
∞
An sin ( nπ
L x ) e−2 π 2 n2 t
L2
g)
Now considering
u ( x , y )= X ( x ) Y ( y )
Plugging this in boundary conditions
X' ' −K1 X=0
Y ' '−K2 Y =0
Thus we have
X a ( x )=sin ( μa x ) μa= aπ
1 K1=−μa
2
Y b ( y ) =sin ( vb x ) vb= bπ
1 K2=−vb
2
This results in
u ( x , y )= X ( x ) Y ( y )
u ( x , y ) =sin ( μa x ) ∗sin ( vb x )
Solution 3
Given
∂u
∂ t = ∂2 u
∂ x2