Theory of Computation Assignment: Chapter 2 Problems and Solutions
VerifiedAdded on 2023/01/23
|23
|2498
|35
Homework Assignment
AI Summary
This document provides solutions to a Theory of Computation assignment, focusing on concepts from Chapter 2 of Peter Linz's "An Introduction to Formal Languages and Automata." The assignment covers deterministic finite accepters (DFA), nondeterministic finite accepters (NFA), and the equivalence between them. Solutions include constructing DFAs and NFAs for various languages, converting NFAs to DFAs, and minimizing the number of states in finite automata. The problems range from basic language recognition to more complex constructions involving regular expressions and automata transformations. The document demonstrates the application of key concepts in automata theory, such as state transition diagrams, language acceptance, and state minimization techniques, providing a comprehensive overview of the subject matter.

Running head: THEORY OF COMPUTATION
Theory of computation
Name of the Student
Name of the University
Author’s Note
Theory of computation
Name of the Student
Name of the University
Author’s Note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
1
0
q0 q1 q2
0
1
0 1
1
THEORY OF COMPUTATION
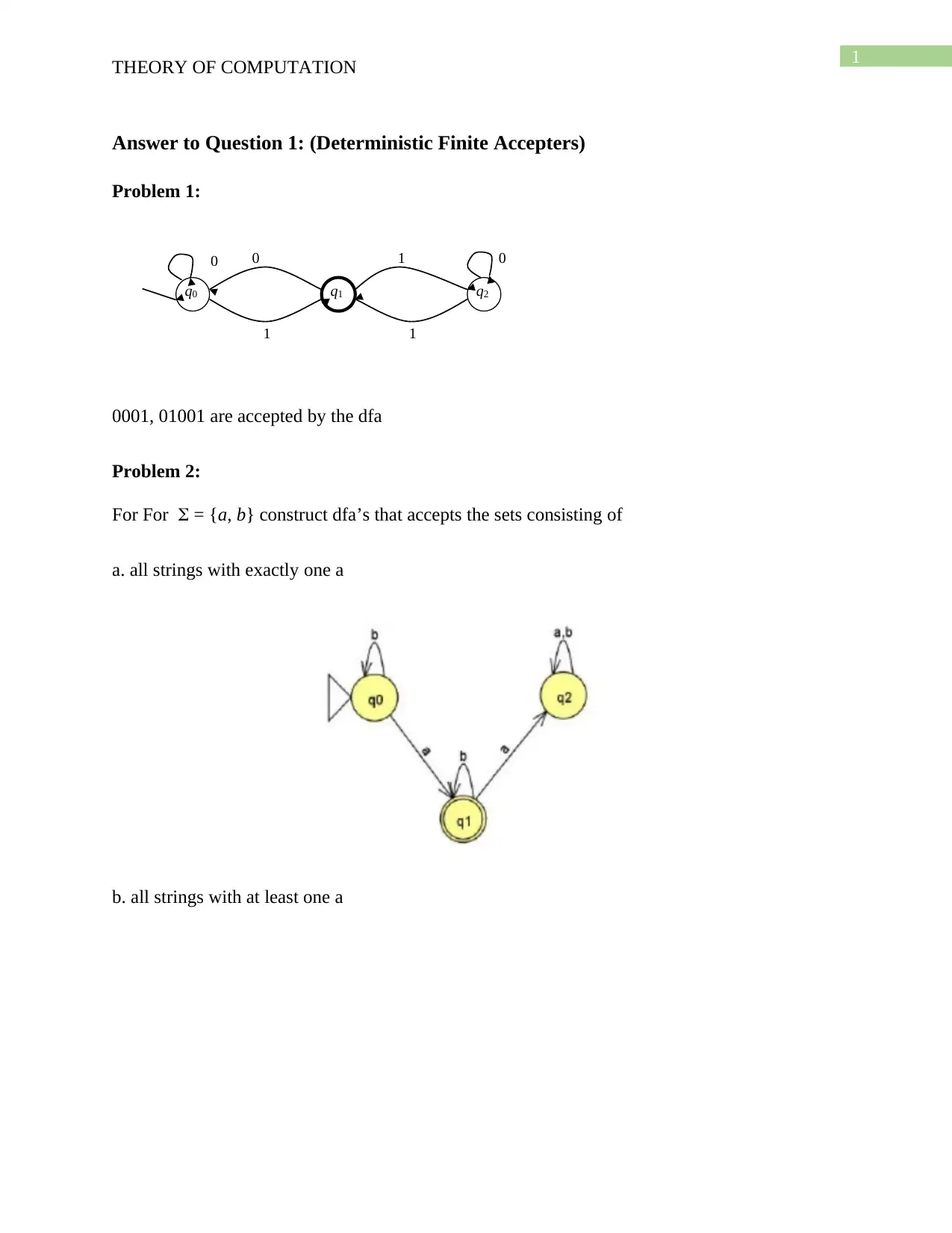
Answer to Question 1: (Deterministic Finite Accepters)
Problem 1:
0001, 01001 are accepted by the dfa
Problem 2:
For For = {a, b} construct dfa’s that accepts the sets consisting of
a. all strings with exactly one a
b. all strings with at least one a
0
q0 q1 q2
0
1
0 1
1
THEORY OF COMPUTATION
Answer to Question 1: (Deterministic Finite Accepters)
Problem 1:
0001, 01001 are accepted by the dfa
Problem 2:
For For = {a, b} construct dfa’s that accepts the sets consisting of
a. all strings with exactly one a
b. all strings with at least one a
2
a a a a
b b a,b
b
b
q0 q1 q2 q3 q4+
THEORY OF COMPUTATION
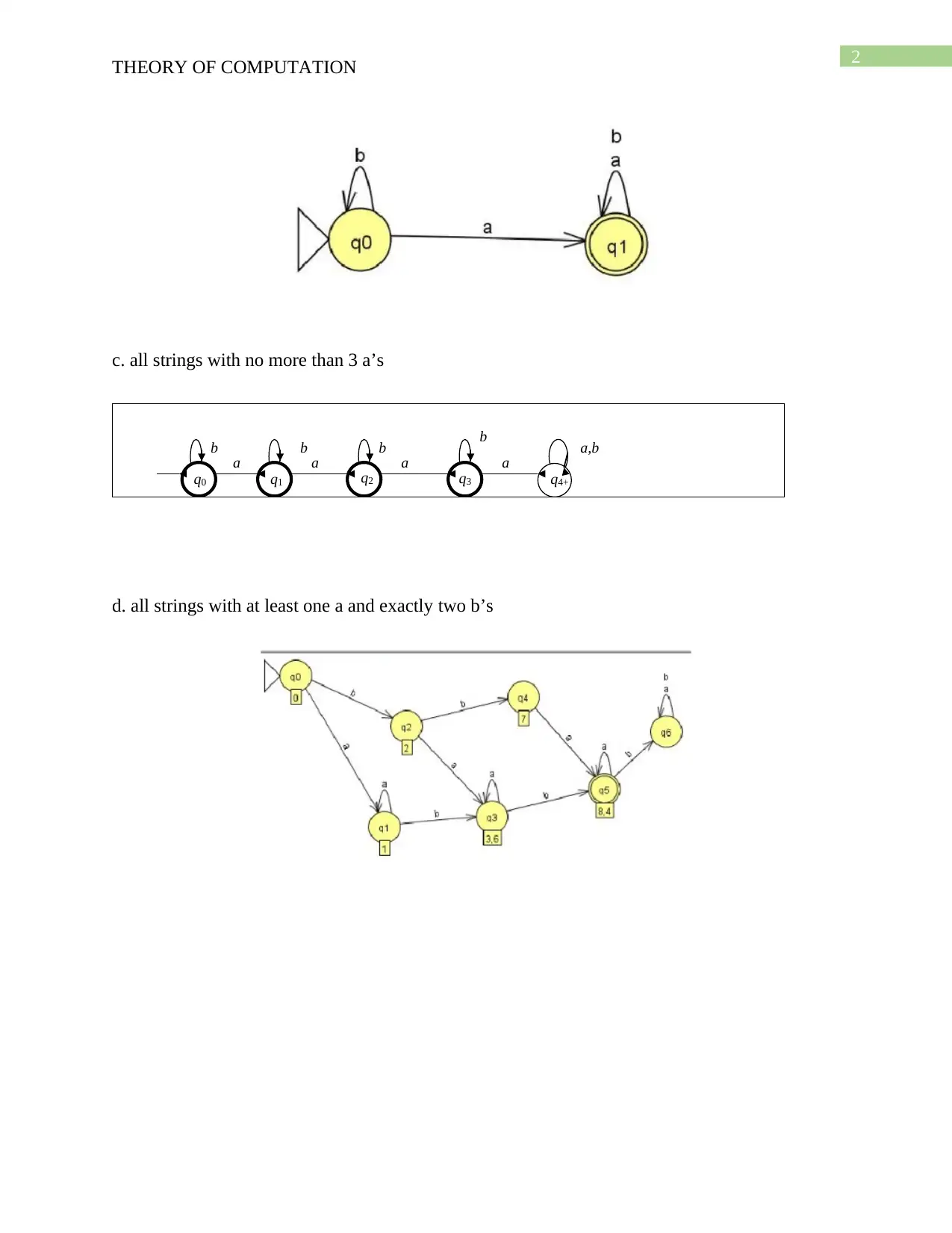
c. all strings with no more than 3 a’s
d. all strings with at least one a and exactly two b’s
a a a a
b b a,b
b
b
q0 q1 q2 q3 q4+
THEORY OF COMPUTATION
c. all strings with no more than 3 a’s
d. all strings with at least one a and exactly two b’s
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

3
THEORY OF COMPUTATION
e. all strings with exactly two a’s and more than two b’s
Problem 3:
Show that if we change fig 2.6 making q3 a nonfinal state and making q0,q1, q2 final states the
resulting dfa accepts
For any dfa the statement is true. If the final and the non-final states are switched then any of the
string leaving in an accepting state leaves the non-final state because we have switched around
THEORY OF COMPUTATION
e. all strings with exactly two a’s and more than two b’s
Problem 3:
Show that if we change fig 2.6 making q3 a nonfinal state and making q0,q1, q2 final states the
resulting dfa accepts
For any dfa the statement is true. If the final and the non-final states are switched then any of the
string leaving in an accepting state leaves the non-final state because we have switched around
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4
THEORY OF COMPUTATION
the different final states. Thus by definition the language that is accepted by the new machine
acts as the compliment of language accepted by original one.
Problem 4:
Generalize the observation in the previous exercise. Specifically, show that if M=Q,∑,∂,q0,F and
It is proved by contradiction suppose M is not a minimal DFA for X then there exists another
DFD Z for A such that Z has fewer states than M. Another DFD Z’ is created by swapping the
acceptance and non-acceptance states of Z. The Z’ recognizes the complement of X. But the
complement of X is just X’ so Z’ recognizes X. Z’has the same number of states as Z and M has
same number of states as M. Thus if it is assumed that Z has strictly fewer states than M then Z’
has strictly fewer states than M, then Z’would have strictly fewer states than M. But since Z’
recognizes X, this contradicts our assumption that M is minimal DFA for X. Therefore M is a
minimal DAA for X.
Problem 5:
a. Dfa for the languages L= {ab5wb2 : w {a, b}*}
b. Dfa for the languages L = { abnam : n ≥ 2, m ≥ 3}
THEORY OF COMPUTATION
the different final states. Thus by definition the language that is accepted by the new machine
acts as the compliment of language accepted by original one.
Problem 4:
Generalize the observation in the previous exercise. Specifically, show that if M=Q,∑,∂,q0,F and
It is proved by contradiction suppose M is not a minimal DFA for X then there exists another
DFD Z for A such that Z has fewer states than M. Another DFD Z’ is created by swapping the
acceptance and non-acceptance states of Z. The Z’ recognizes the complement of X. But the
complement of X is just X’ so Z’ recognizes X. Z’has the same number of states as Z and M has
same number of states as M. Thus if it is assumed that Z has strictly fewer states than M then Z’
has strictly fewer states than M, then Z’would have strictly fewer states than M. But since Z’
recognizes X, this contradicts our assumption that M is minimal DFA for X. Therefore M is a
minimal DAA for X.
Problem 5:
a. Dfa for the languages L= {ab5wb2 : w {a, b}*}
b. Dfa for the languages L = { abnam : n ≥ 2, m ≥ 3}
5
THEORY OF COMPUTATION
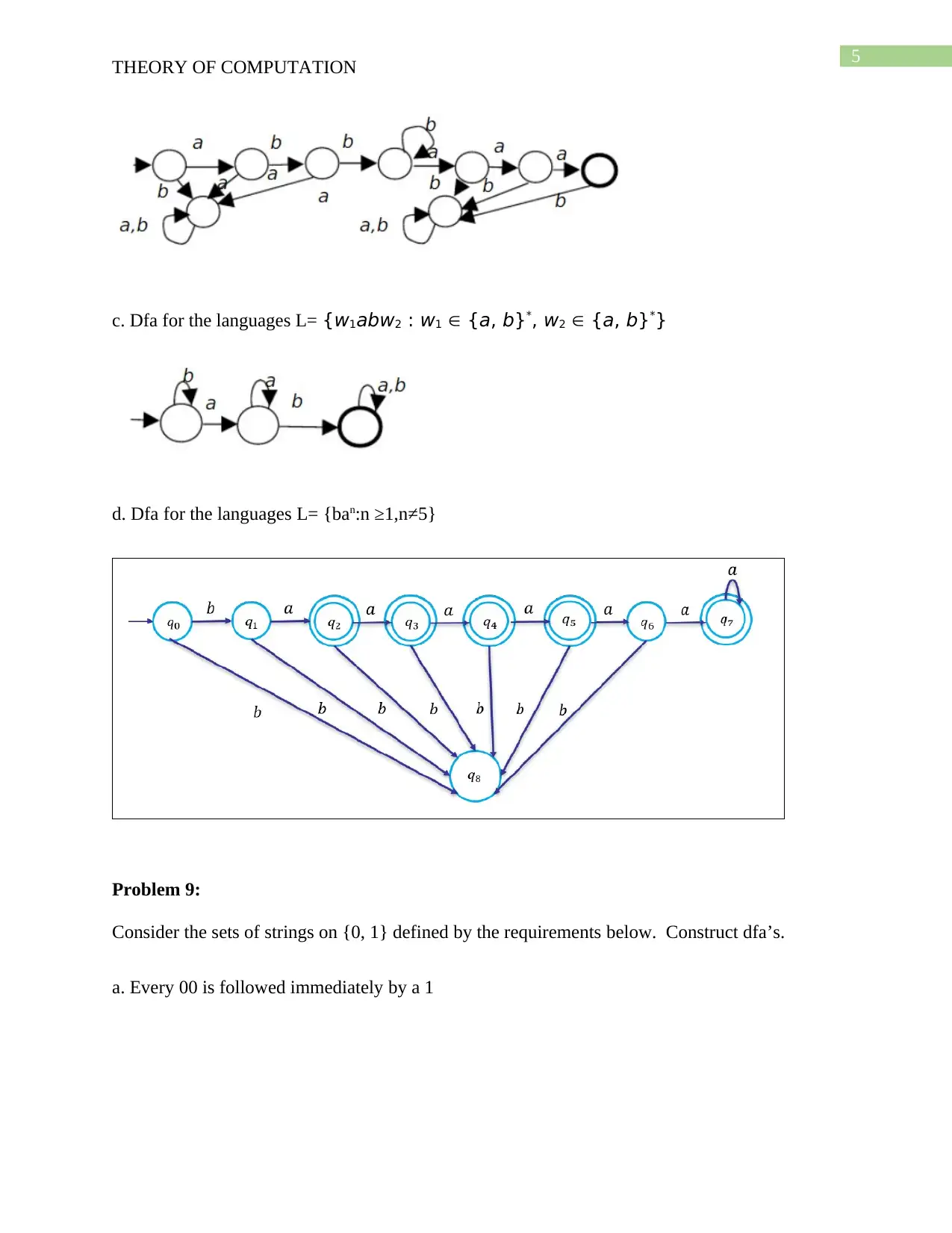
c. Dfa for the languages L= {w1abw2 : w1 {a, b}*, w2 {a, b}*}
d. Dfa for the languages L= {ban:n ≥1,n≠5}
Problem 9:
Consider the sets of strings on {0, 1} defined by the requirements below. Construct dfa’s.
a. Every 00 is followed immediately by a 1
THEORY OF COMPUTATION
c. Dfa for the languages L= {w1abw2 : w1 {a, b}*, w2 {a, b}*}
d. Dfa for the languages L= {ban:n ≥1,n≠5}
Problem 9:
Consider the sets of strings on {0, 1} defined by the requirements below. Construct dfa’s.
a. Every 00 is followed immediately by a 1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
6
1 0 0
1
0 0,1
1
1 0 0
0
0
1 0
0
1
1
0 0
1
1
0
1
0
THEORY OF COMPUTATION
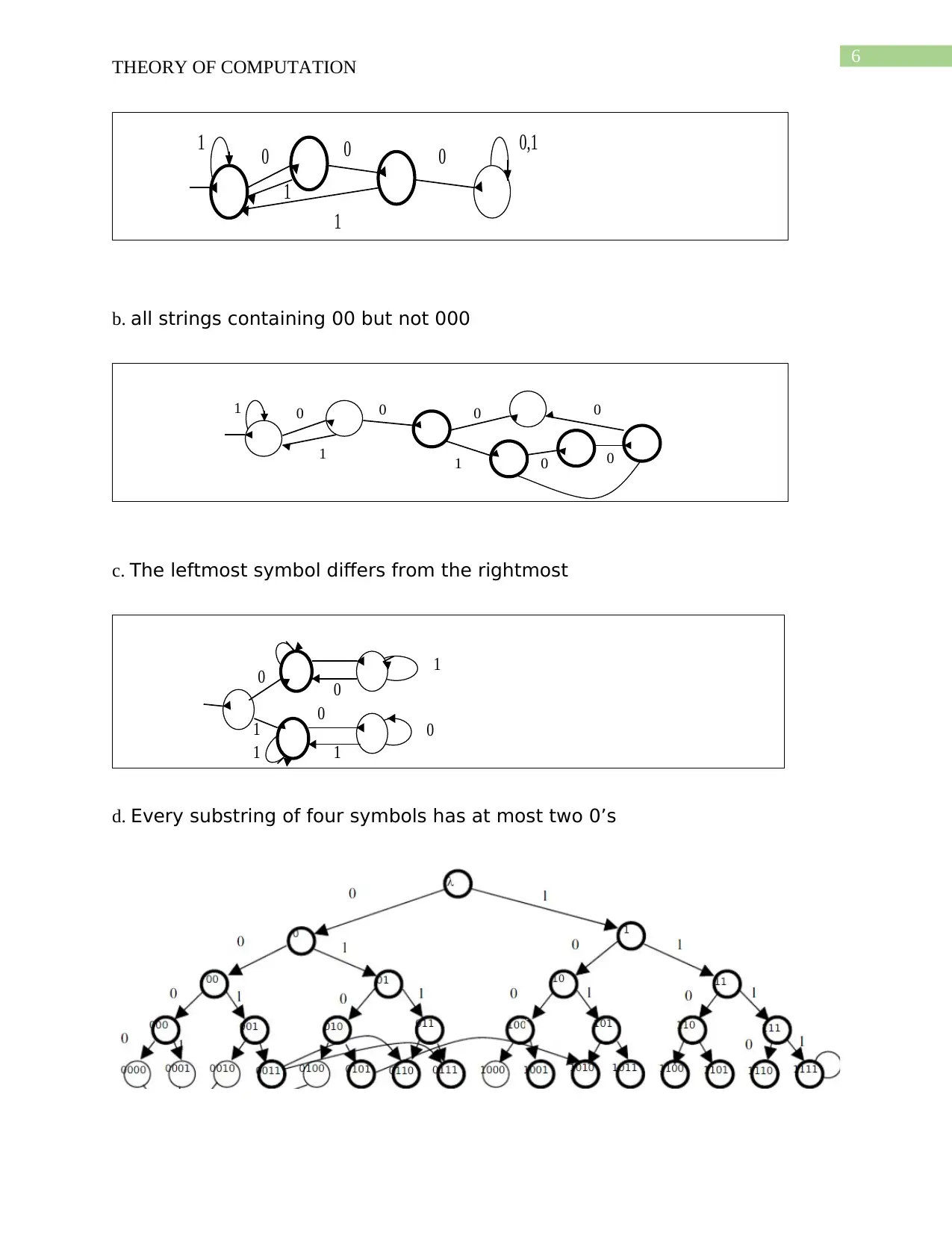
b. all strings containing 00 but not 000
c. The leftmost symbol differs from the rightmost
d. Every substring of four symbols has at most two 0’s
1 0 0
1
0 0,1
1
1 0 0
0
0
1 0
0
1
1
0 0
1
1
0
1
0
THEORY OF COMPUTATION
b. all strings containing 00 but not 000
c. The leftmost symbol differs from the rightmost
d. Every substring of four symbols has at most two 0’s
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7
THEORY OF COMPUTATION
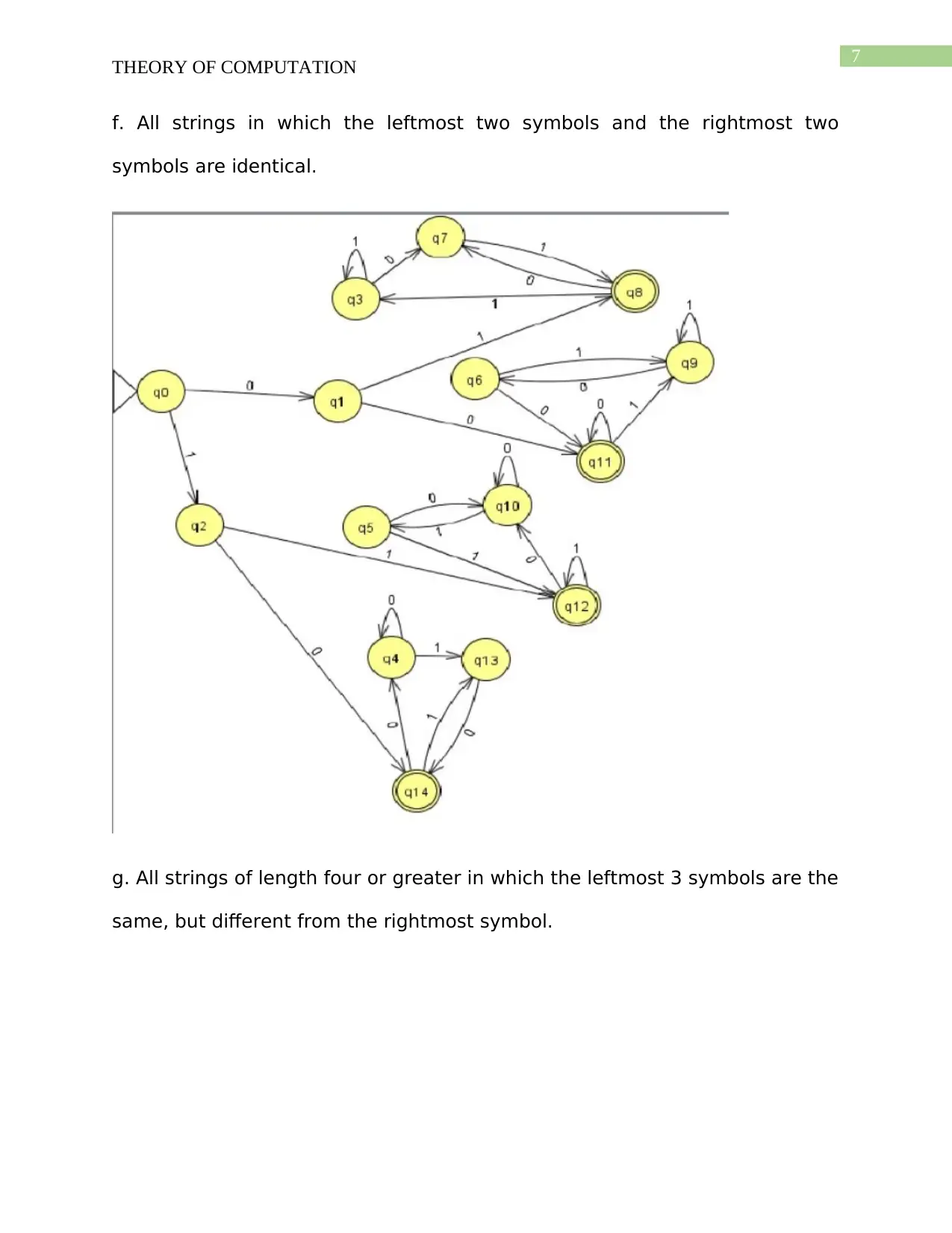
f. All strings in which the leftmost two symbols and the rightmost two
symbols are identical.
g. All strings of length four or greater in which the leftmost 3 symbols are the
same, but different from the rightmost symbol.
THEORY OF COMPUTATION
f. All strings in which the leftmost two symbols and the rightmost two
symbols are identical.
g. All strings of length four or greater in which the leftmost 3 symbols are the
same, but different from the rightmost symbol.

8
THEORY OF COMPUTATION
Answer to Question 2: (Non Deterministic Finite Accepters)
Problem 1:
Provide in details the claim made in the previous section that if in a transition graph there is a
walk labeled w, there must be some walk labeled w of length no more than Λ + (1 + Λ) |w|
If between two vertices vi and vj there is any walk labeled w, then there must be some
walk labeled w of length no more than Λ + (1 + Λ)|w|, where Λ is the number of λ-edges in the
graph.
⇒ Computing δ ∗ (vi , w): evaluate all walks of length at most Λ + (1 + Λ)|w| originating at
some vi .
Problem 2:
Find a dfa that accepts the language defined by the nfa
THEORY OF COMPUTATION
Answer to Question 2: (Non Deterministic Finite Accepters)
Problem 1:
Provide in details the claim made in the previous section that if in a transition graph there is a
walk labeled w, there must be some walk labeled w of length no more than Λ + (1 + Λ) |w|
If between two vertices vi and vj there is any walk labeled w, then there must be some
walk labeled w of length no more than Λ + (1 + Λ)|w|, where Λ is the number of λ-edges in the
graph.
⇒ Computing δ ∗ (vi , w): evaluate all walks of length at most Λ + (1 + Λ)|w| originating at
some vi .
Problem 2:
Find a dfa that accepts the language defined by the nfa
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
9
THEORY OF COMPUTATION
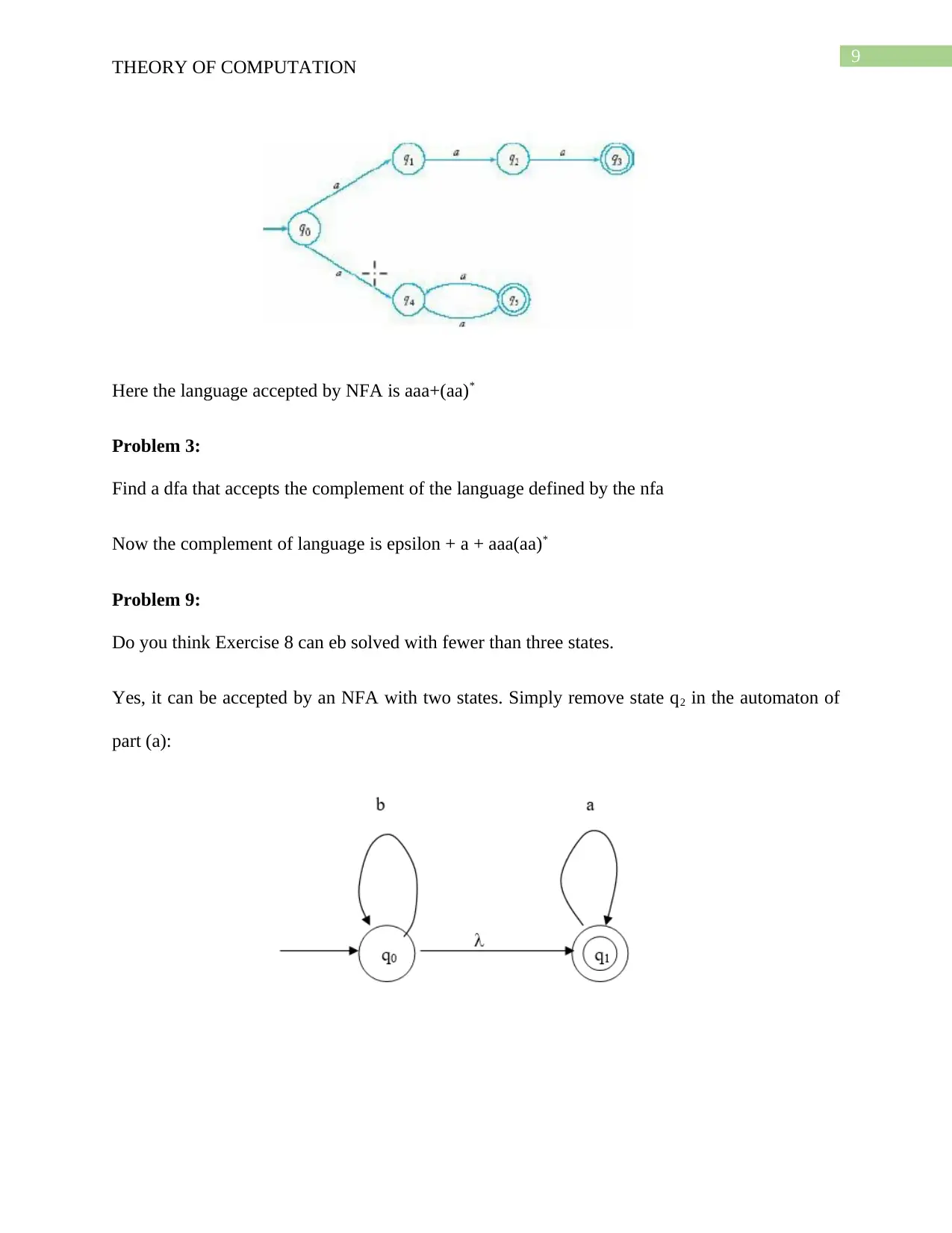
Here the language accepted by NFA is aaa+(aa)*
Problem 3:
Find a dfa that accepts the complement of the language defined by the nfa
Now the complement of language is epsilon + a + aaa(aa)*
Problem 9:
Do you think Exercise 8 can eb solved with fewer than three states.
Yes, it can be accepted by an NFA with two states. Simply remove state q2 in the automaton of
part (a):
THEORY OF COMPUTATION
Here the language accepted by NFA is aaa+(aa)*
Problem 3:
Find a dfa that accepts the complement of the language defined by the nfa
Now the complement of language is epsilon + a + aaa(aa)*
Problem 9:
Do you think Exercise 8 can eb solved with fewer than three states.
Yes, it can be accepted by an NFA with two states. Simply remove state q2 in the automaton of
part (a):
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

10
THEORY OF COMPUTATION
Answer to Question 3
Problem 1
Initial state:
Transitions from {q0}:
Transitions from {q1, q2}:
Transitions from {q0, q1, q2}:
{q0}
{q0}
a
b
{q0, q1, q2}
{q1, q2}
{q0}
a
b
{q0, q1, q2}
{q1, q2}
a
b
THEORY OF COMPUTATION
Answer to Question 3
Problem 1
Initial state:
Transitions from {q0}:
Transitions from {q1, q2}:
Transitions from {q0, q1, q2}:
{q0}
{q0}
a
b
{q0, q1, q2}
{q1, q2}
{q0}
a
b
{q0, q1, q2}
{q1, q2}
a
b
11
THEORY OF COMPUTATION
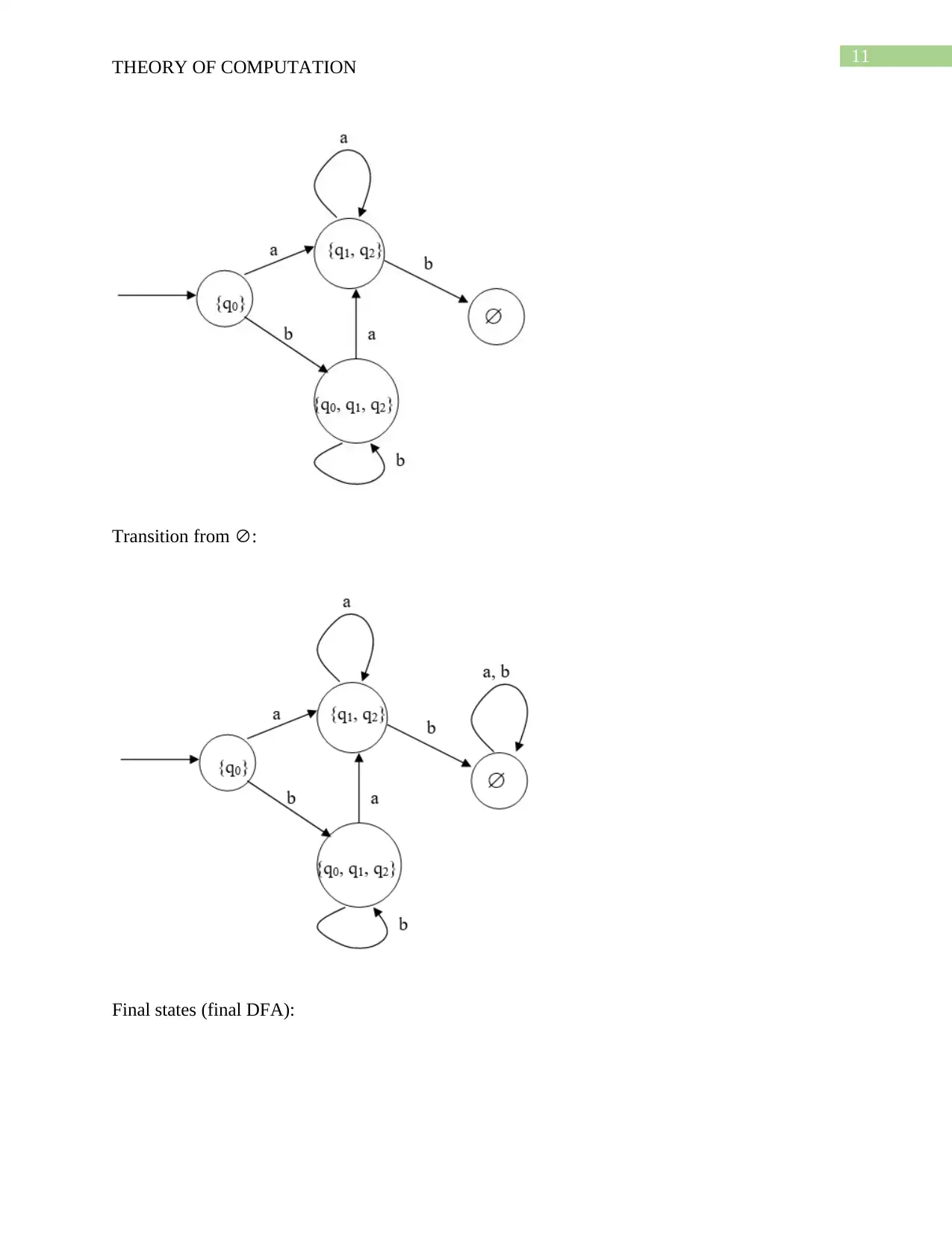
Transition from :
Final states (final DFA):
THEORY OF COMPUTATION
Transition from :
Final states (final DFA):
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 23
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





