Mechanical Engineering: Thermodynamics and Engine Analysis Homework
VerifiedAdded on 2023/04/11
|5
|584
|398
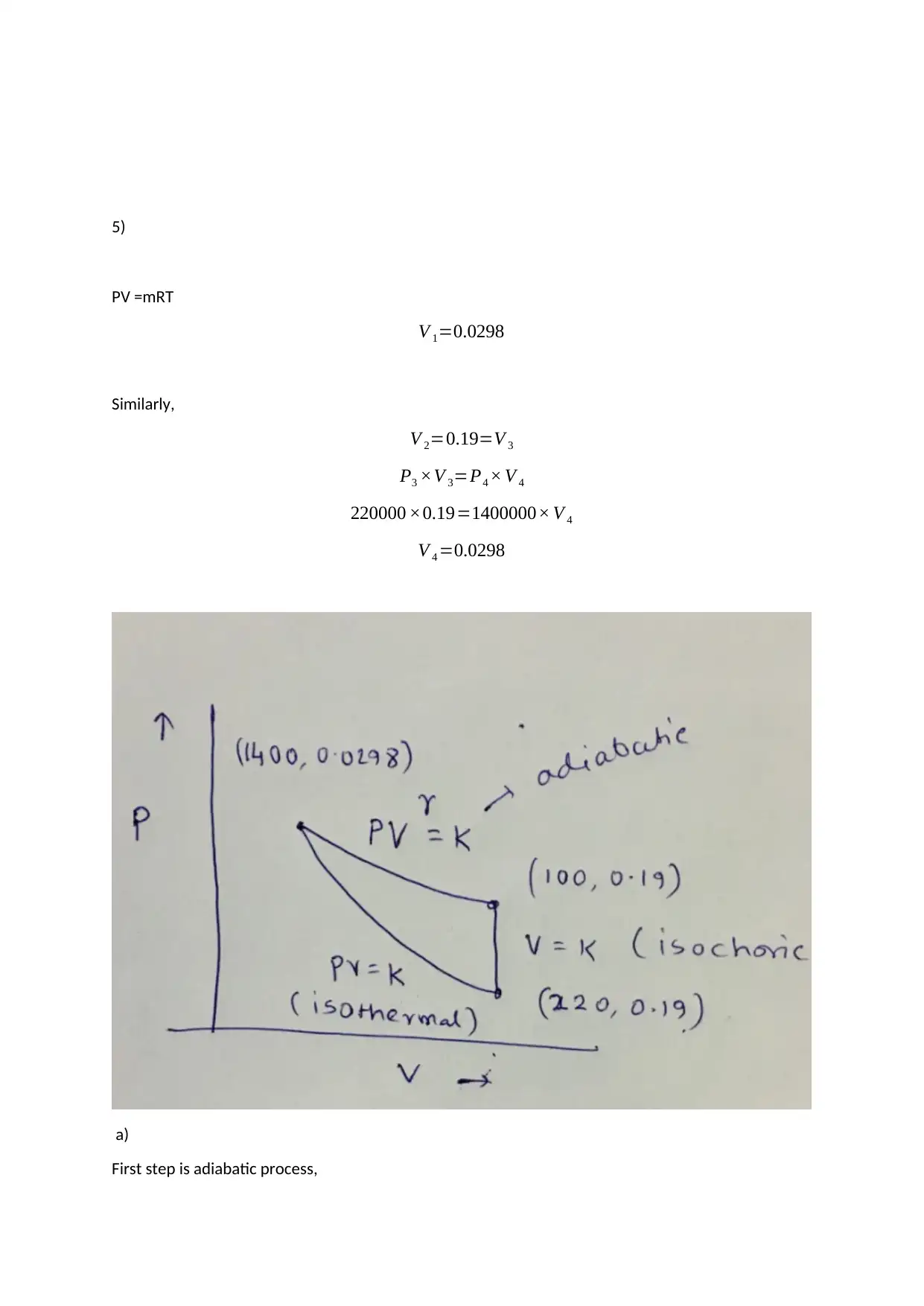
Homework Assignment
AI Summary
This document presents a detailed solution to a mechanical engineering homework assignment focusing on thermodynamics and engine analysis. The solution encompasses a variety of problems, including calculations related to adiabatic processes, internal energy changes, and work done in thermodynamic cycles. It analyzes engine performance, determining parameters such as mechanical efficiency, brake power, specific fuel consumption, and thermal efficiencies (indicated and brake). The document provides step-by-step solutions, including the application of relevant formulas and principles, offering a comprehensive understanding of the concepts involved. Furthermore, the solution covers the analysis of multi-cylinder engines, calculating key parameters such as the mean effective pressure and engine dimensions. The document provides a complete breakdown of the calculations and analysis, making it a valuable resource for students studying mechanical engineering.
1 out of 5






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)