Thermodynamics Assignment - ME101, Fall 2024: Gas Laws and Systems
VerifiedAdded on 2022/08/08
|8
|1645
|42
Homework Assignment
AI Summary
This thermodynamics assignment delves into fundamental concepts, beginning with definitions of open, closed, diathermal, adiabatic, and isolated systems, along with fixed, movable, permeable, impermeable, diathermal, and adiabatic walls. The assignment then explores the First Law of Thermodynamics, including energy conservation equations for both isolated and open systems, with explanations of different power types. It proceeds to examine the three ideal gas laws (Boyle's, Charles', and Avogadro's), their mathematical relations, and underlying assumptions. Furthermore, the assignment defines a polytropic process and determines the polytropic index for specific cases, such as isobaric, isochoric, isothermal, and isentropic processes. Finally, it concludes with a practical problem involving a piston-cylinder assembly, requiring calculations of heat transfer for different system configurations. The document includes detailed solutions and relevant references to support the answers.

Running Head: THERMODYNAMICS 1
Thermodynamics
Name
Institution
Thermodynamics
Name
Institution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

THERMODYNAMICS 2
Thermodynamics
Question 1
Thermodynamic fundamentals and definitions
a) A thermodynamic system consists of matter contained in a region of space delineated by
a closed surface that split up the system from its environment. Describe what is meant if a
system is said to be:
i) Open
A thermodynamic system is said to be open if the system undergoes external interactions. This
means that the system interacts with both mass and energy (Moran, 2010). By interacting here,
there is exchange of properties as well as energy.
ii) Closed
A closed thermodynamic system on the other hand only interacts with energy but not with
matter. Thus, the system does not allow for exchange of elements but can obtain energy from
another system.
iii) Diathermal
This is a closed thermodynamic system that has been made alternately permeable and
impermeable to radiation and conductive heat. As in the case of closed thermodynamic system,
this system allows interaction with heat energy but only in form of radiation and conduction.
iv) Adiabatic
This process happens without transfer of heat or mass of elements between a thermodynamic
system and its environs. This means that whether there is interaction or no interaction with other
systems, their property remains the same before or after interaction.
v) Isolated
An isolated one does not interact with other thermodynamic systems. It is far of from other
thermodynamic systems such that it cannot interact with them. There is no exchange of matter or
energy in this type of thermodynamic system.
Thermodynamics
Question 1
Thermodynamic fundamentals and definitions
a) A thermodynamic system consists of matter contained in a region of space delineated by
a closed surface that split up the system from its environment. Describe what is meant if a
system is said to be:
i) Open
A thermodynamic system is said to be open if the system undergoes external interactions. This
means that the system interacts with both mass and energy (Moran, 2010). By interacting here,
there is exchange of properties as well as energy.
ii) Closed
A closed thermodynamic system on the other hand only interacts with energy but not with
matter. Thus, the system does not allow for exchange of elements but can obtain energy from
another system.
iii) Diathermal
This is a closed thermodynamic system that has been made alternately permeable and
impermeable to radiation and conductive heat. As in the case of closed thermodynamic system,
this system allows interaction with heat energy but only in form of radiation and conduction.
iv) Adiabatic
This process happens without transfer of heat or mass of elements between a thermodynamic
system and its environs. This means that whether there is interaction or no interaction with other
systems, their property remains the same before or after interaction.
v) Isolated
An isolated one does not interact with other thermodynamic systems. It is far of from other
thermodynamic systems such that it cannot interact with them. There is no exchange of matter or
energy in this type of thermodynamic system.

THERMODYNAMICS 3
b) A thermodynamic system can often be decomposed into smaller subsystems that can
themselves be considered as thermodynamic systems. The separation between two
subsystems is referred to as a wall or boundary. The enclosure which separates a system
from its environment consists of one or several walls. Describe what is meant if a wall is
said to be:
i) Fixed
A wall is said to be fixed if it remains in a single place. By remaining in a single place simply
means its intact and cannot be moved from one region to another. The separation between the
subsystem do not change position. It remains intact in the environment.
ii) Movable
Movable walls are the thermodynamic walls that shift their location. They wall or boundary can
change its position and shift to a new region. It can be relocated to a new region or place.
iii) Permeable
This is a wall that allows transfer of quantity. This means its surface contains pores which
permits transfer of quantity.
iv) Impermeable
Impermeable ones do not allow the transfer of quantity between them. This means the surface
lacks pores which can permit transfer of energy through the interface.
v) Diathermal
This wall allows exchange of heat between the system and surroundings through the boundary
wall.
vi) Adiabatic
This type of wall does not allow heat or matter to pass through it.
(c) Write out in full, the definition of the First Law of Thermodynamics. Also, provide the
energy conservation equations for both an isolated system as well as an open system. In the case
of an open system, give an explanation for each form/type of power that can occur when a
system interacts with its environment.
b) A thermodynamic system can often be decomposed into smaller subsystems that can
themselves be considered as thermodynamic systems. The separation between two
subsystems is referred to as a wall or boundary. The enclosure which separates a system
from its environment consists of one or several walls. Describe what is meant if a wall is
said to be:
i) Fixed
A wall is said to be fixed if it remains in a single place. By remaining in a single place simply
means its intact and cannot be moved from one region to another. The separation between the
subsystem do not change position. It remains intact in the environment.
ii) Movable
Movable walls are the thermodynamic walls that shift their location. They wall or boundary can
change its position and shift to a new region. It can be relocated to a new region or place.
iii) Permeable
This is a wall that allows transfer of quantity. This means its surface contains pores which
permits transfer of quantity.
iv) Impermeable
Impermeable ones do not allow the transfer of quantity between them. This means the surface
lacks pores which can permit transfer of energy through the interface.
v) Diathermal
This wall allows exchange of heat between the system and surroundings through the boundary
wall.
vi) Adiabatic
This type of wall does not allow heat or matter to pass through it.
(c) Write out in full, the definition of the First Law of Thermodynamics. Also, provide the
energy conservation equations for both an isolated system as well as an open system. In the case
of an open system, give an explanation for each form/type of power that can occur when a
system interacts with its environment.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

THERMODYNAMICS 4
The law states that energy can neither be created nor destroyed in an isolated system. Energy can
only be transformed from one state to another without any loss. For instance, water in a dam has
potential energy, when its channeled downhill to power station it is transformed to kinetic energy
which is later transformed to electrical energy by magnets.
For an isolated system: Ki + Ui = Kf + Uf. E = K + U, where E = mechanical energy and k is
kinetic energy (Haddad, 2009).
For an open system:ECV = (Ek + Ep + H)in - (Ek + Ep + H)out + Q + WS
When an open system interacts with its environment, an instantaneous power is the power that
has immediate force on the open system.
Question 2
(a) There are three fundamental gas laws which describe the relationship between the
pressure, temperature, volume and amount of an ideal gas. Provide the name,
mathematical relation, and explanation of each of these three ideal gas laws.
Boyle’s gas law: The absolute pressure exerted by a specified mass of an ideal gas is inversely
proportional to the volume it occupies if the temperatures and quantity of gas remain unchanged
within a closed system. Equation P1V1 = P2V2 Where P is pressure and V is volume. In simple
terms, the product of pressure and volume remains constant throughout the system (Gaskell,
2017). This can be demonstrated PV = k. where k is a constant.
Charles’ Law: The volume of an ideal gas at constant pressure is directly proportional to the
absolute temperature (Gaskell, 2017). Equation:
V 1
T 1 = V 2
T 2
Where V is the volume of the gas and T is its temperature in kelvin K. the ratio of volume to
temperature is constant throughout the system. This assumes that there is no external interference
to the system.
Avogadro’s law states that equal volumes of gases at the same temperature and pressure contain
equal numbers of molecules (Kondepudi, 2014).
The law states that energy can neither be created nor destroyed in an isolated system. Energy can
only be transformed from one state to another without any loss. For instance, water in a dam has
potential energy, when its channeled downhill to power station it is transformed to kinetic energy
which is later transformed to electrical energy by magnets.
For an isolated system: Ki + Ui = Kf + Uf. E = K + U, where E = mechanical energy and k is
kinetic energy (Haddad, 2009).
For an open system:ECV = (Ek + Ep + H)in - (Ek + Ep + H)out + Q + WS
When an open system interacts with its environment, an instantaneous power is the power that
has immediate force on the open system.
Question 2
(a) There are three fundamental gas laws which describe the relationship between the
pressure, temperature, volume and amount of an ideal gas. Provide the name,
mathematical relation, and explanation of each of these three ideal gas laws.
Boyle’s gas law: The absolute pressure exerted by a specified mass of an ideal gas is inversely
proportional to the volume it occupies if the temperatures and quantity of gas remain unchanged
within a closed system. Equation P1V1 = P2V2 Where P is pressure and V is volume. In simple
terms, the product of pressure and volume remains constant throughout the system (Gaskell,
2017). This can be demonstrated PV = k. where k is a constant.
Charles’ Law: The volume of an ideal gas at constant pressure is directly proportional to the
absolute temperature (Gaskell, 2017). Equation:
V 1
T 1 = V 2
T 2
Where V is the volume of the gas and T is its temperature in kelvin K. the ratio of volume to
temperature is constant throughout the system. This assumes that there is no external interference
to the system.
Avogadro’s law states that equal volumes of gases at the same temperature and pressure contain
equal numbers of molecules (Kondepudi, 2014).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

THERMODYNAMICS 5
V 1
n1 = V 2
n 2 where v is volume, n is the amount of the gas. Thus the ratio of volume to the
amount of gas is constant throughout the system.
b) These three ideal gas laws rely on making several simplifying assumptions, which
fortunately for us, prove to be more than reasonable for mathematically governing
most “every day” applications. Please list these assumptions.
Assumptions are all gas particles are in constant motion. Volume of the molecules is considered
insignificant likened to the volume of the container. Another assumption is that gas molecules
collide in completely elastic collisions (Bansal, 2010).
c) What is meant if a thermodynamic process is said to be “polytropic”?
When pVn = constant. If an ideal gas obeys this relation, then the thermodynamic process is
regarded as polytropic.
What is the polytropic index for the following specific cases whereby a process is:
(i) Isobaric
The polytropic index is 0.
(ii) Isochoric
The poytropic index is infinity
(iii) Isothermal
The polytropic index is 1.
(iv) Isentropic
The polytropic index is gamma.
(d) If you have 1 Kg of a gas with a specific gas constant of 260 J/Kg.K which is compressed
according to a polytropic process such that the temperature of the gas increases by 60 degC,
determine the polytropic index of this process if 3000 J of work is done on the system (Kim,
2012).
260J/KG
V 1
n1 = V 2
n 2 where v is volume, n is the amount of the gas. Thus the ratio of volume to the
amount of gas is constant throughout the system.
b) These three ideal gas laws rely on making several simplifying assumptions, which
fortunately for us, prove to be more than reasonable for mathematically governing
most “every day” applications. Please list these assumptions.
Assumptions are all gas particles are in constant motion. Volume of the molecules is considered
insignificant likened to the volume of the container. Another assumption is that gas molecules
collide in completely elastic collisions (Bansal, 2010).
c) What is meant if a thermodynamic process is said to be “polytropic”?
When pVn = constant. If an ideal gas obeys this relation, then the thermodynamic process is
regarded as polytropic.
What is the polytropic index for the following specific cases whereby a process is:
(i) Isobaric
The polytropic index is 0.
(ii) Isochoric
The poytropic index is infinity
(iii) Isothermal
The polytropic index is 1.
(iv) Isentropic
The polytropic index is gamma.
(d) If you have 1 Kg of a gas with a specific gas constant of 260 J/Kg.K which is compressed
according to a polytropic process such that the temperature of the gas increases by 60 degC,
determine the polytropic index of this process if 3000 J of work is done on the system (Kim,
2012).
260J/KG

THERMODYNAMICS 6
P is pressure, V is volume, R is the rate and T the temperature.
PV=nRT
P * 1 = 1 * 260 * 60, P = 15600
(PV)n= C
(15600 * 1)n = C
15600n = 260
n = log 260/15600 = -4.09
Question 3
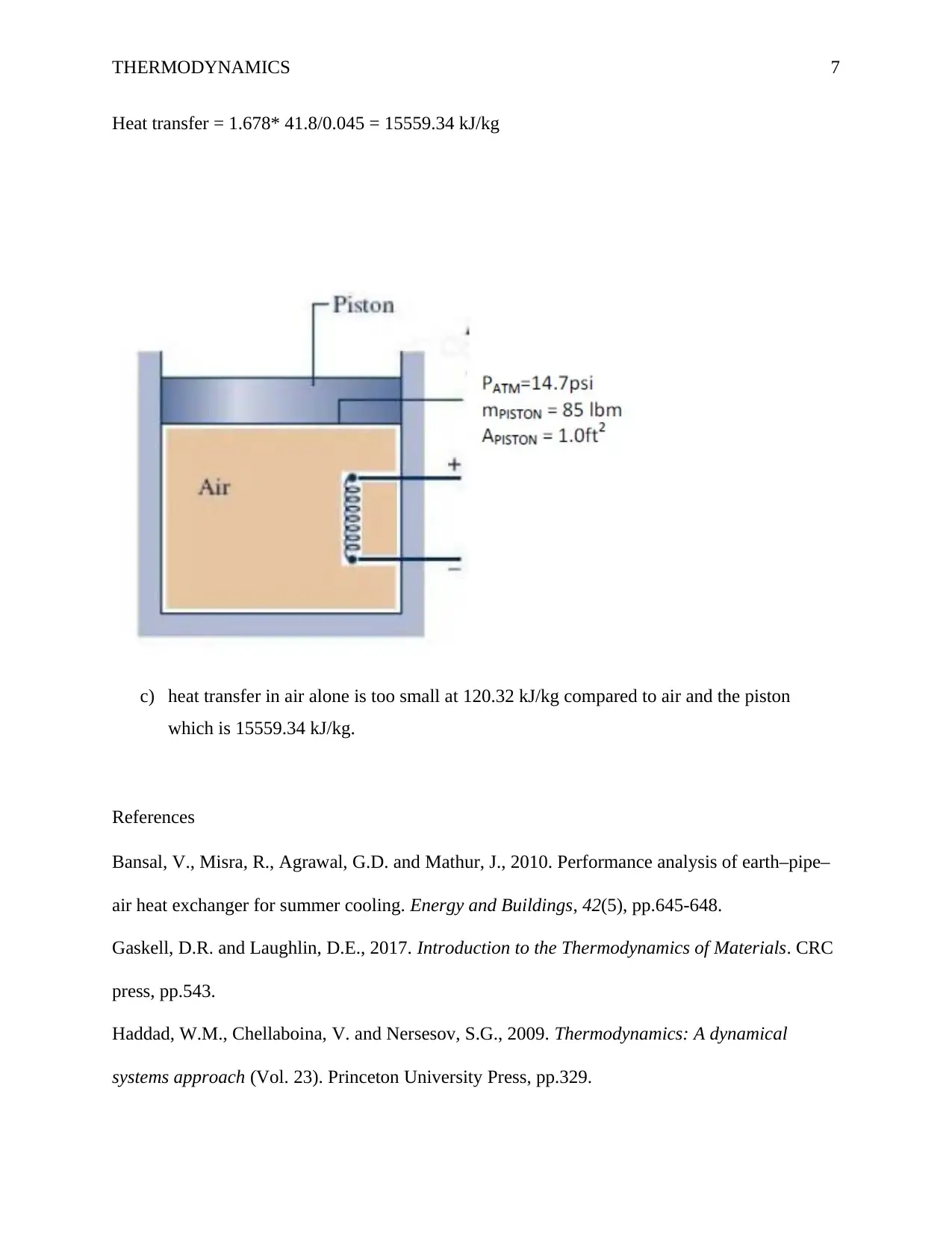
0.35 kg’s of air is contained in a vertical piston‐cylinder assembly fitted with an electrical
resistor. The atmospheric pressure is 101.325 kPa and the piston has a mass of 45 kg and a face
area of 0.12 m2. An electrical current is passed through a resistive heating element which causes
the air contained within the cylinder to expand in volume by 0.045 m3. During this process, the
specific energy of the air increases by 41.8 kJ/kg. Assuming that the piston-cylinder assembly is
insulated (and thus there is no heat loss to the environment) and frictional losses between the
cylinder wall and the piston can be considered to be negligible, determine the heat transfer from
the heating element to the air for a system consisting of:
(a) the air alone,
P1 V 1=P2 V 2
a) P=F / A=3.5/0.12=29.16
V 2=29.16∗0.45 /101.325=120.32 kJ /kg
Heat transfer = 120.32 kJ/kg
b) the air and the piston
P=F / A=(45+0.35)∗10/0.12=3779.16
V 2=3779.16∗0.045 /101.325=1.678 kJ /m 3
P is pressure, V is volume, R is the rate and T the temperature.
PV=nRT
P * 1 = 1 * 260 * 60, P = 15600
(PV)n= C
(15600 * 1)n = C
15600n = 260
n = log 260/15600 = -4.09
Question 3
0.35 kg’s of air is contained in a vertical piston‐cylinder assembly fitted with an electrical
resistor. The atmospheric pressure is 101.325 kPa and the piston has a mass of 45 kg and a face
area of 0.12 m2. An electrical current is passed through a resistive heating element which causes
the air contained within the cylinder to expand in volume by 0.045 m3. During this process, the
specific energy of the air increases by 41.8 kJ/kg. Assuming that the piston-cylinder assembly is
insulated (and thus there is no heat loss to the environment) and frictional losses between the
cylinder wall and the piston can be considered to be negligible, determine the heat transfer from
the heating element to the air for a system consisting of:
(a) the air alone,
P1 V 1=P2 V 2
a) P=F / A=3.5/0.12=29.16
V 2=29.16∗0.45 /101.325=120.32 kJ /kg
Heat transfer = 120.32 kJ/kg
b) the air and the piston
P=F / A=(45+0.35)∗10/0.12=3779.16
V 2=3779.16∗0.045 /101.325=1.678 kJ /m 3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
THERMODYNAMICS 7
Heat transfer = 1.678* 41.8/0.045 = 15559.34 kJ/kg
c) heat transfer in air alone is too small at 120.32 kJ/kg compared to air and the piston
which is 15559.34 kJ/kg.
References
Bansal, V., Misra, R., Agrawal, G.D. and Mathur, J., 2010. Performance analysis of earth–pipe–
air heat exchanger for summer cooling. Energy and Buildings, 42(5), pp.645-648.
Gaskell, D.R. and Laughlin, D.E., 2017. Introduction to the Thermodynamics of Materials. CRC
press, pp.543.
Haddad, W.M., Chellaboina, V. and Nersesov, S.G., 2009. Thermodynamics: A dynamical
systems approach (Vol. 23). Princeton University Press, pp.329.
Heat transfer = 1.678* 41.8/0.045 = 15559.34 kJ/kg
c) heat transfer in air alone is too small at 120.32 kJ/kg compared to air and the piston
which is 15559.34 kJ/kg.
References
Bansal, V., Misra, R., Agrawal, G.D. and Mathur, J., 2010. Performance analysis of earth–pipe–
air heat exchanger for summer cooling. Energy and Buildings, 42(5), pp.645-648.
Gaskell, D.R. and Laughlin, D.E., 2017. Introduction to the Thermodynamics of Materials. CRC
press, pp.543.
Haddad, W.M., Chellaboina, V. and Nersesov, S.G., 2009. Thermodynamics: A dynamical
systems approach (Vol. 23). Princeton University Press, pp.329.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

THERMODYNAMICS 8
Kim, K.Y., Kim, S.C. and Kim, M.S., 2012. Experimental studies on the heating performance of
the PTC heater and heat pump combined system in fuel cells and electric vehicles. International
Journal of Automotive Technology, 13(6), pp.971-977.
Kondepudi, D. and Prigogine, I., 2014. Modern thermodynamics: from heat engines to
dissipative structures. John Wiley & Sons, pp.98.
Moran, M.J., Shapiro, H.N., Boettner, D.D. and Bailey, M.B., 2010. Fundamentals of
engineering thermodynamics. John Wiley & Sons, pp.453.
Kim, K.Y., Kim, S.C. and Kim, M.S., 2012. Experimental studies on the heating performance of
the PTC heater and heat pump combined system in fuel cells and electric vehicles. International
Journal of Automotive Technology, 13(6), pp.971-977.
Kondepudi, D. and Prigogine, I., 2014. Modern thermodynamics: from heat engines to
dissipative structures. John Wiley & Sons, pp.98.
Moran, M.J., Shapiro, H.N., Boettner, D.D. and Bailey, M.B., 2010. Fundamentals of
engineering thermodynamics. John Wiley & Sons, pp.453.
1 out of 8