Time Value of Money and Its Applications in Finance

This report provides a comprehensive overview of the time value of money, a fundamental concept in finance. It explains the core principles, including the idea that money available at the present time is worth more than the same amount in the future due to its potential earning capacity. The report delves into the reasons behind this, such as risk, inflation, and opportunity cost, and explains how these factors influence financial decisions. It illustrates the concept with practical examples, including calculations of present value and its application in security valuation and capital budgeting. The report also discusses the limitations of the time value of money and its application in the valuation of securities and capital budgeting, highlighting the importance of the interest rate in these calculations. The report concludes by demonstrating how the time value of money is a crucial tool for making informed investment decisions and reducing arbitrage opportunities, providing examples for better understanding.

Business Finance
1

Time value of money:
Time value of money is the concept which establishes the reasons for difference in the value
of the money today and in the future period. It states that a sum of money is worth more if
received today than at some other time (Adelaja, 2015). This concept will be better
understood with the help of an example. Mr. X has $10 today, if he invests this sum for a
period of 6 month, then he would receive $12 at the expiry of the stated period. The
difference between $10 and $12 is due to earning capacity of the money, which is called time
value. The major principle in finance states that if money has the capacity to earn interest,
then the amount which is received first is of more worth. Few reasons for which money has
time value are as follows:
- Risk: given an option to receive $100 today or after 1 year, a person would accept today.
It is so because it eliminates the risk factor, removes uncertainty of not receiving money
some time.
- Inflation: more goods can be purchased today then after 1 year. This is so because he
inflation rate increases and declines the purchasing power of money. (Bierman & Smidt,
2010)
- Opportunity cost: money received today can be invested to earn interest income.
Whereas if amount is received after a year we will lose the interest for one year.
The process which helps to calculate of value present value of money which is to be received
in future if called discounting. Discounting cash flow technique is one of the major
components in security pricing and investment decision. (Peterson & Fabozzi, 2012)
The most important tool in time value of money is interest rate. It is the most important factor
on which whole of the application of this concept depends. It is important that the investor
calculate his required rate of properly, else the whole result may conclude to something else.
Calculation of this rate of return is the crucial part; it depends on lot of conditions and
assumptions. (Rivenbark, Vogt, & Marlowe, 2009) Change in any of the condition may result
in calculation of wrong return. This is one of the greatest limitations of time value of money.
Time value of money in valuation of securities:
Time value of money helps calculate the worth of securities. It helps investor decide the
maximum price they should pay for a given security, so that they can earn their desired rate
of interest. When an investor invests a sum in a security, he is promised by the company that
2

he would earn interest income on this principle amount. The worth of money which is
invested today should be minimum present value of incomes which the investor is to receive
in future. Therefore, by discounting the future cash flows from a security, we get the
maximum price of the security which the investor should be willing to pay. (Seitz & Ellison,
2009) It not only calculates the value of securities, it also helps calculate the value of
business which helps investor analyse the worth of the company. Concept of time value of
money helps reduce arbitrage opportunities.
The following example will help understand this concept better. Say there is a security A
which is expected to earn $50 annually for 5 years and at the end of year 5, it will also
redeem the face value of $1000. Given the required rate of return is 11%, how much an
investor should invest today. For this we need to calculate the present value of the cash flows:
Year
Cash
Flows PV factor @11% PV of Cash Flows
1 50 0.9009 45.05
2 50 0.8116 40.58
3 50 0.7312 36.56
4 50 0.6587 32.94
5 1050 0.5935 623.12
Total 778.25
Therefore given the required rate of return of 11%, the investor should not invest more than
$778.25 today.
Time value of money in Capital budgeting:
Time value of money helps in taking investment decisions. Capital budgeting is one of most
used financial tool which helps the investor in making decisions. Suppose we are provided
with two opportunities for investment, both these have same cash flows but the timing of
these cash flows is different. Time value of money will help analyse the present value of
these cash flows and help the investor decide which the better option is. (Shapiro, 2007)
There are other tools in capital budgeting like discounted pay back, internal rate of return, etc,
which assist in decision making. The option with the higher present value of net inflows
3

should be opted for maximum returns. But this also has few limitations. As discussed earlier,
a rate is required to discount the cash flows. Calculation of this rate for capital budgeting is
one of the most complex steps. Wrong calculations will lead to wrong results and losses.
The following example will help understand this concept better. Let say, we have two
projects, K and L. following are the cash flows from both the projects:
Cash Flows from Project K Cash Flows from Project L
Year Cash Flows Year Cash Flows
0 -50000 0 -40000
1 10000 1 8000
2 15000 2 16000
3 17000 3 17000
4 16000 4 16000
5 20000 5 11000
We see that the net cash flow from both the project is $28000. Given a rate of return of 7%,
we will calculate the present values of cash flows from both the project in order to evaluate
the better option.
Cash Flows from Project K
Yea
r Cash Flows PV factor @7% PV of Cash Flows
0 -50000
1.000
0 -50,000.00
1 10000
0.934
6 9,345.79
2 15000
0.873
4 13,101.58
3 17000
0.816
3 13,877.06
4 16000
0.762
9 12,206.32
5 20000 0.713 14,259.72
4

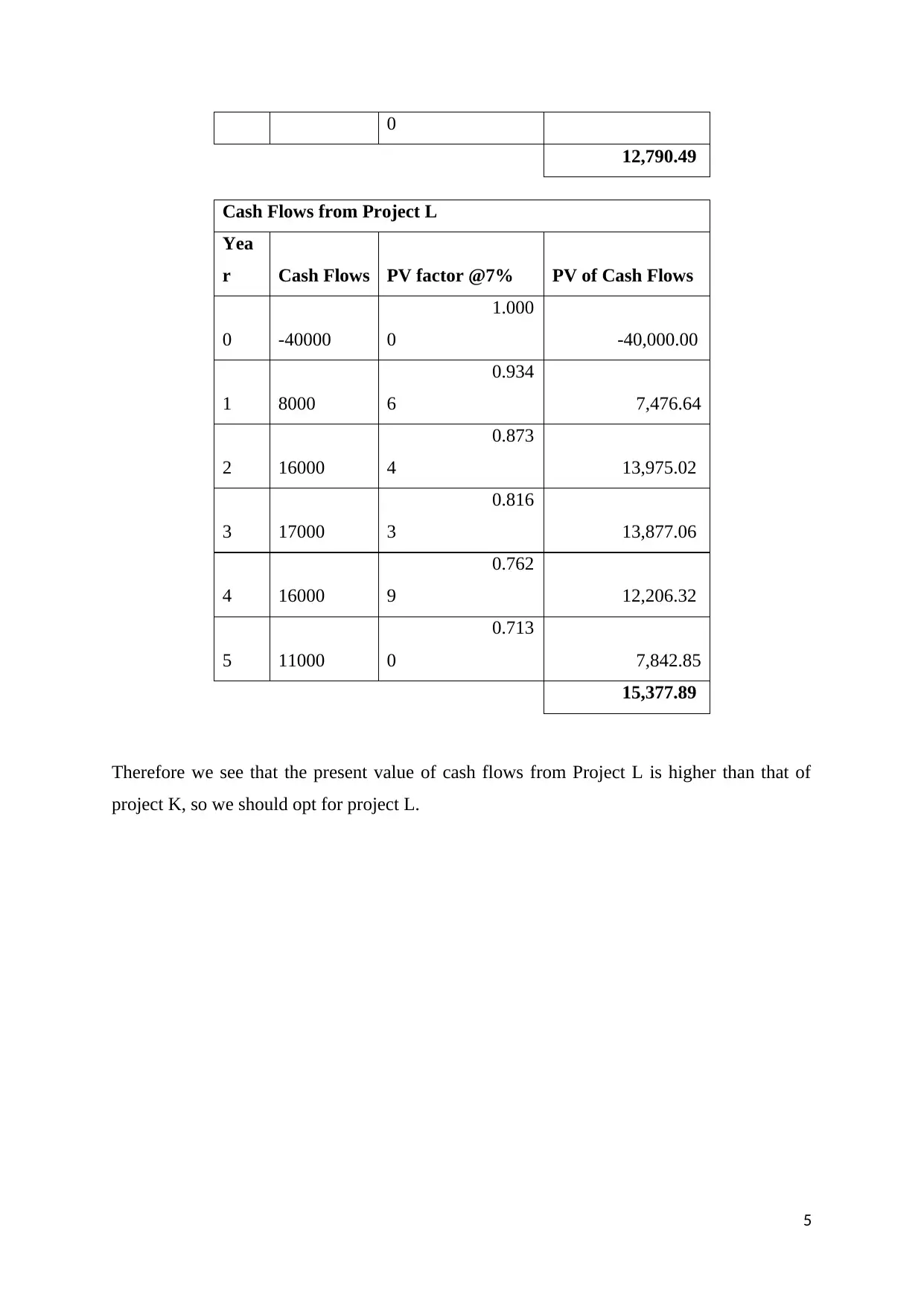
0
12,790.49
Cash Flows from Project L
Yea
r Cash Flows PV factor @7% PV of Cash Flows
0 -40000
1.000
0 -40,000.00
1 8000
0.934
6 7,476.64
2 16000
0.873
4 13,975.02
3 17000
0.816
3 13,877.06
4 16000
0.762
9 12,206.32
5 11000
0.713
0 7,842.85
15,377.89
Therefore we see that the present value of cash flows from Project L is higher than that of
project K, so we should opt for project L.
5

Bibliography
Adelaja, T. (2015). Capital Budgeting: Investment Appraisal Techniques Under Certainty.
Chicago: CreateSpace Independent Publishing Platform .
Bierman, H., & Smidt, S. (2010). The Capital Budgeting Decision. Boston: Routledge.
Peterson, P. P., & Fabozzi, F. J. (2012). Capital Budgeting. New York, NY: Wiley.
Rivenbark, W. C., Vogt, J., & Marlowe, J. (2009). Capital Budgeting and Finance: A Guide
for Local Governments. Washington, D.C.: ICMA Press.
Seitz, N., & Ellison, M. (2009). Capital Budgeting and Long-Term Financing Decisions.
New York: Thomson Learning.
Shapiro, A. C. (2007). Capital Budgeting and Investment Analysis. New Jersey: Wiley.
6