TM355 TMA 01: Comprehensive Computer Science Assignment Solution

This document presents a comprehensive solution to a computer science assignment, addressing key concepts such as the sampling theorem, 16-QAM modulation, Shannon's equation, refractive index, and radiofrequency analysis. The solution includes detailed calculations for determining bit rates and minimum bandwidth, a signal constellation diagram for 16-QAM, and explanations of Shannon's theorem. It also covers multimode distortion, dispersion, attenuation in optical fibers, and the differences between Fourier series and Fourier transforms. Furthermore, the assignment delves into radiofrequency analysis, including frequency allocation and radio propagation mechanisms within the ionosphere. The document provides diagrams, calculations, and explanations to aid in understanding these complex topics.

Computer Science Assignment
Student Name
Institution Affiliation

QUESTION 1
a) A signal extending from 0 to 15.0 kHz is sampled at a rate of 20% greater
than the minimum sampling rate given by the sampling theorem. Each
sample is coded as an 8-bit binary word and transmitted as a sequence of
eight binary symbols.
i. How many bits per second are generated by this process?
According to the sampling theorem, the sampling frequency should be at least
twice the highest frequency in a signal. That said, a 20% margin higher than
the highest frequency signal has been provided.
Thus, the sampling rate will be given as follows;
Sampling Rate = 120*30/100 = 36.0kHz.
Bitrate = Bits per second*Samples per second*No. of channels;
=8*36000*8
Bits per second (bit rate) = 2,304,400 bits per second
You can divide the bit rate by 1000 so that you have 2,304.4kbps
ii. Calculate the minimum bandwidth required to transmit bits at this
rate over a noise-free channel?
The minimum bandwidth is equal to the Nyquist bandwidth.
Therefore the minimum bandwidth (BW)min=W=Rb/2= (2304.4/2) =1152.2
(Cheng, Ruan, and Wu, 2005)

b. Sketch a signal constellation diagram for 16-QAM. Label the axes of
your diagram and explain what they stand for. State, with a brief explanation,
how many bits each point represents.
A rectangular QAM modulation is an equivalent of superimposing two ASK
signals on quadrature carriers. The size of each symbol is given by the formula
k=log2(M). Therefore, for a 16-QAM modulation:
k=log2(16) = 4
The next step is to generate a gray coded 16-QAM constellation using K-Maps
Using a 4 variable K-
Map (given that the symbol size as calculated above is 4), the following table is
obtained:
AB/CD 00 01 11 10
00 0000 0001 0011 0010
01 0100 0101 0111 0110
11 1100 1101 1111 1110
10 1000 1001 1011 1010
first K-Map table
Replacing AB and CD with four amplitude levels {-3, -1, +1, +3} gives the following
table:
(What you do with the table I have provided up there is just to replace those digital
digits with those amplitude levels were -3(00), -1(01), +1(11), and +3(10)

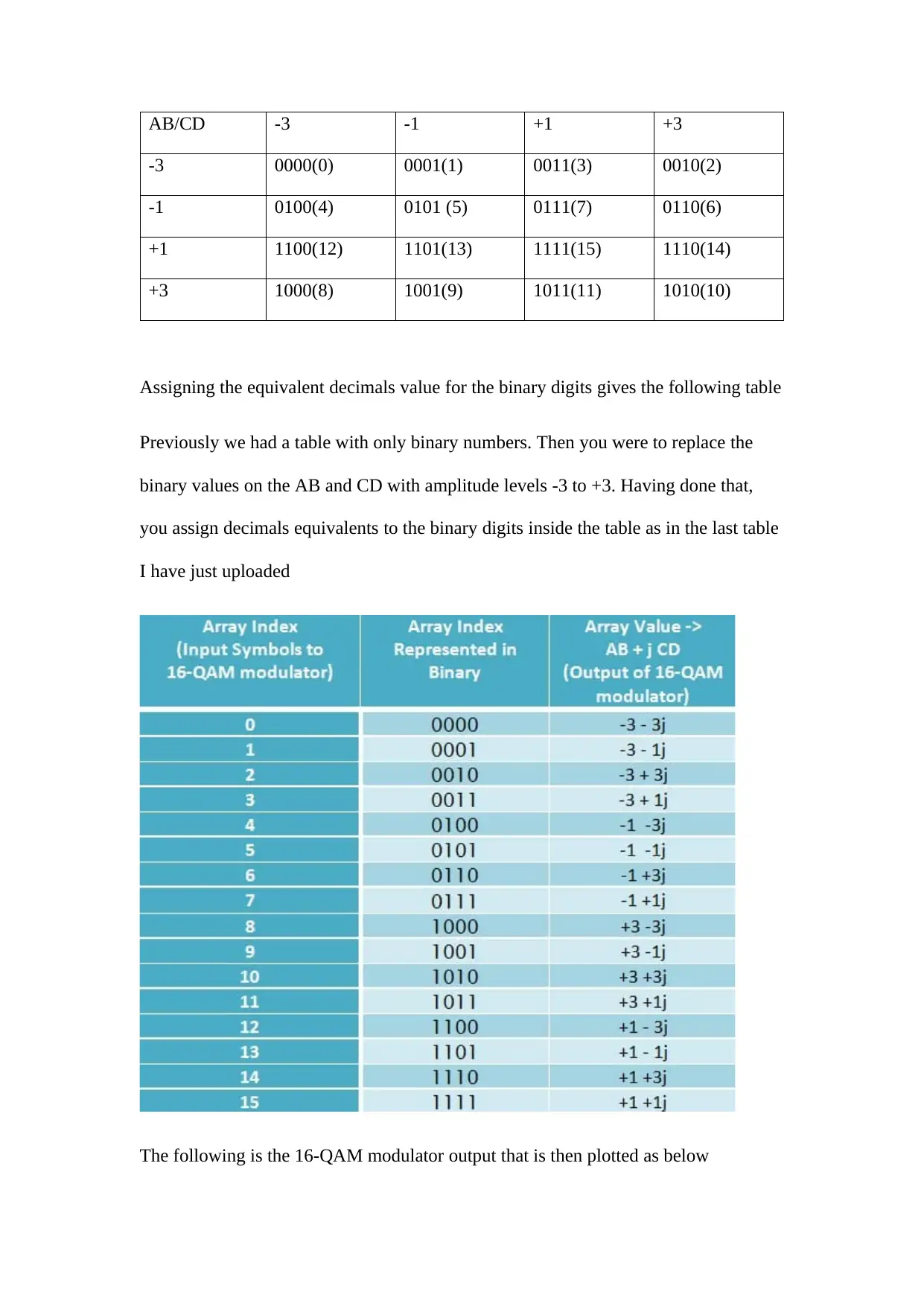
AB/CD -3 -1 +1 +3
-3 0000(0) 0001(1) 0011(3) 0010(2)
-1 0100(4) 0101 (5) 0111(7) 0110(6)
+1 1100(12) 1101(13) 1111(15) 1110(14)
+3 1000(8) 1001(9) 1011(11) 1010(10)
Assigning the equivalent decimals value for the binary digits gives the following table
Previously we had a table with only binary numbers. Then you were to replace the
binary values on the AB and CD with amplitude levels -3 to +3. Having done that,
you assign decimals equivalents to the binary digits inside the table as in the last table
I have just uploaded
The following is the 16-QAM modulator output that is then plotted as below

c.
i. State Shannon’s equation, explaining each of the terms in full. What are the
underlying assumptions for Shannon’s equation to be valid?
The Shannon-Hartley theorem state that “The maximum amount of error-free digital
data that can be transmitted over a communications channel with a
specified bandwidth in the presence of noise”
-The terms in the theory are an information source, a transmitter, the signal, and the
receiver.
Information source
It provides the limit with which the data will be compressed within the entropy of the
theorem.
Transmitter
Refers to the medium of communication through which the message is transmitted.
Signal
Refers to the main message or the wave that carries the message being transmitted
through the medium.

Receiver
It refers to the destination of the signal being transferred from the initial source of
information and from the transmitter.
Information source- it is basically where the coded information comes from
ii. Capacity
c= BW.log2(1+SNR)bps
c= 6.log2(1+SN36)
c= 6.log2(1+0.59)
c= 6.log2(1.59)
c= 6.log2(1.6)
c= 1.8(1.6)
c= 28.8
(Shannon, 1948)
Question 2
a. Refractive Index
It focuses on the relationship between the velocity of light traveling in a vacuum
and the velocity when it travels over some specified medium. In this case, it can be

referred to the extent or the rate in which light is transmitted over some medium.
Since its normally greater compared to the cladding index, it causes refraction to
occur regularly over the transmission media, and at the interface incidences.
Therefore, it allows the attenuation of the light beam and reduces eliminates the
reflecting light over a given distance.
b. Multimode distortion
As the name suggests, it is a deformation that occurs through multiple modes,
which is caused by the difference in velocity of the optical signal being transmitted.
The distortion simply results from the delay caused by the rays traveling through the
optical fiber, where rays with shorter paths will be transmitted faster while those with
shorter paths will take longer. Besides, it occurs both at single and multiple
wavelengths, though it does not depend fully on them. The distortion poses several
effects the communication in that, it causes degradation of the transmitted signal and a
loss in the distribution.
c. Dispersion
It refers to the spread of rays traveling through an optical fiber. The wave tends to
broaden in the transmission process due to the effects of some features including the
diameter of the core and the width of the laser line. Hence, due to its increase with the
increase in distance traveled, it causes an effect known as the Intersymbol
Interference. The effect it has on the optical fiber communication is that it causes
overlapping of the pulses, making them less detectable.
d. Attenuation
It is a reduction in intensity experienced in a signal light that is being transmitted
through a fiber. The media components like connectors and cables play a major role

in its occurrence. Also, its happening involves both the single and multi-modes of
transmission. However, it can be overcome through the availing of sufficient light
within the data link to be used. It works to limit the long-distance transmission of the
digital signals.

Question 3
a. Fourier Series and Fourier Transform
Fourier series refers to the application of sines and cosines whose sum exists in
an infinite form, in expanding a periodic function. It majorly applies the relationship
of the cosine and sine functions known as orthogonality. On the other hand, Fourier
transform refers to the generalized series of a complex Fourier, set on certain limits.
The only similarity that exists between the two is that both of them work on the
signals, irrespective of the activity occurring. Nonetheless, the first difference
between them is that Fourier series focuses on the actions of periodic signals, while
Fourier Transform targets the activities of the aperiodic signals. Secondly, Fourier
series is applied in the decomposition of signals to form the base elements while
Fourier transform is utilized in the analysis of signals in several domains (Duffin, and
Schaeffer, 1952)
b. Drawing diagrams
i. A square wave
5
00
1 1 2
000
1
.2 1
.0 0
.8 0
.6 0
.4 0
.2
Amplitu
de (volts)
Frequ
ency (Hz)

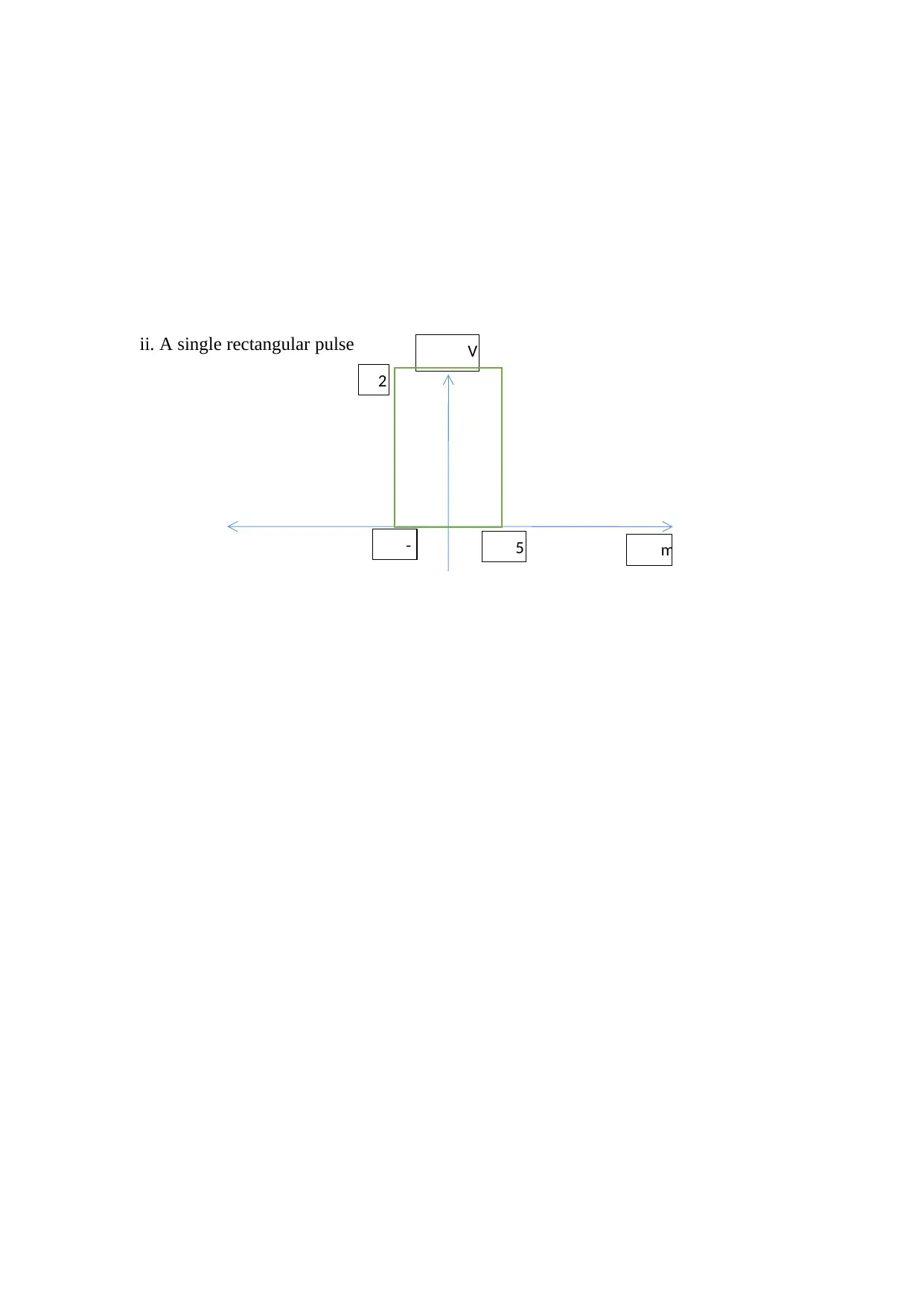
ii. A single rectangular pulse V
olts
m5-
2

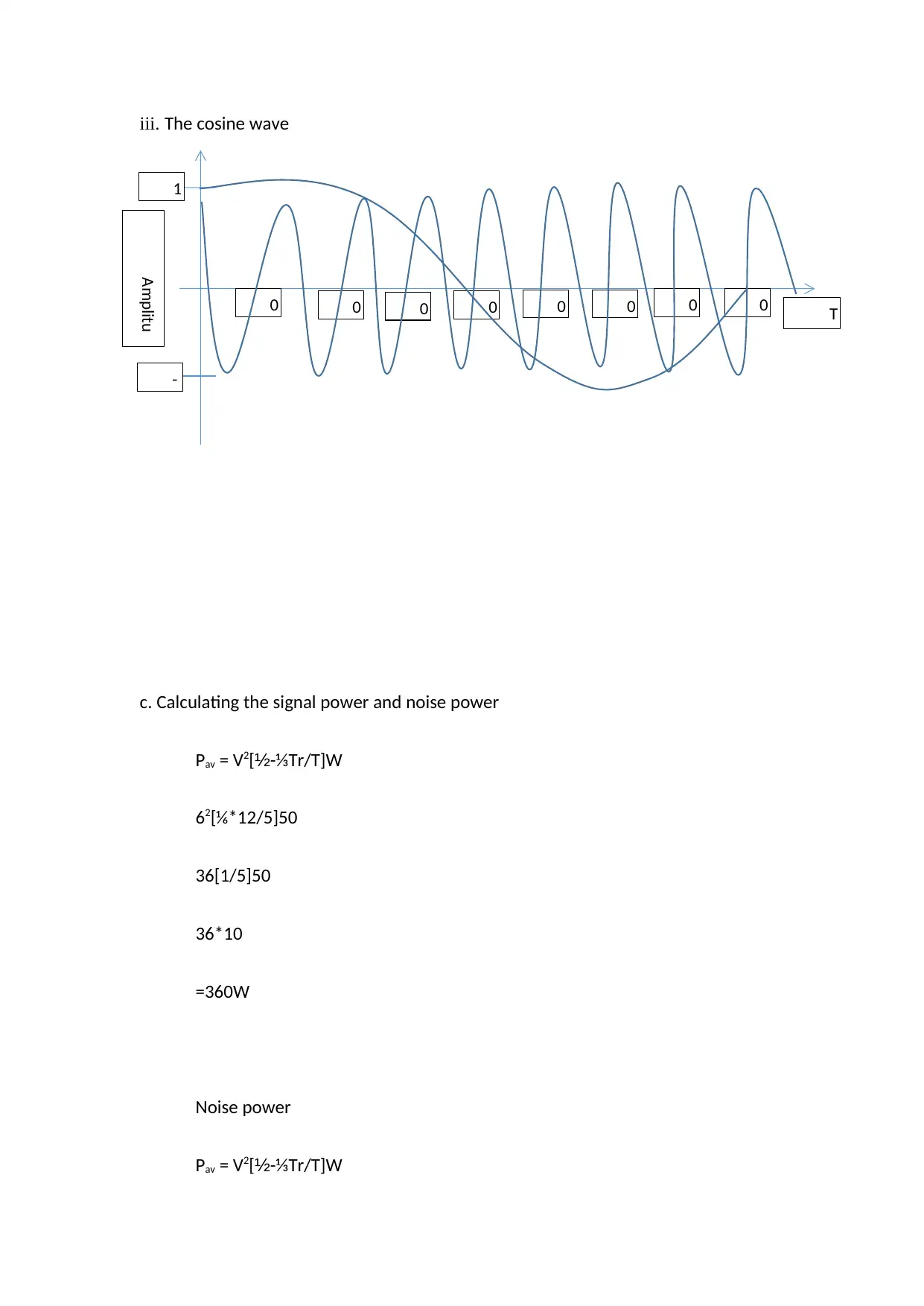
iii. The cosine wave
c. Calculating the signal power and noise power
Pav = V2[½-⅓Tr/T]W
62[⅙*12/5]50
36[1/5]50
36*10
=360W
Noise power
Pav = V2[½-⅓Tr/T]W
0 0 0 0 0 0 0 0
1
-
T
Amplitu
de (volts)

52[⅙*12/6]50
25[1/3]50
=416.7W
Signal to noise ratio
360/360=417/360
1:1.16
=1:1.2
=1:1

Running head: COMPUTER SCIENCE 13
Question 4
a. Radiofrequency analysis
Frequency allocation refers to the process of allocating and regulating the electromagnetic
spectrum into the various bands of radio frequency. A combination of wavelengths in relation to
the frequency ranges define clearly what the electromagnetic spectrum is. Besides, photon
energies also play an important part in the constituents of the spectrum. It works through the
correspondences of the wavelengths and frequencies. The ranges in the frequency are subdivided
into given bands, where the components of the frequency, specifically electromagnetic waves,
are defined differently. The waves include microwaves, radio waves, ultraviolet and gamma rays,
with the latter being at the peak.
Significantly, the governments of the various nations take the responsibility of allocating and
regulating the frequency. Harmonization of the radio frequencies has been adopted by most of
the governments due to the fact that the propagation surpasses the national boundaries. The move
has enabled the formation of working relationships among many government leaders, where the
frequencies have been standardized to allow their full utilization.
Furthermore, a unique definition has been provided to frequency allocation, by the
International Telecommunication Union. It has termed it as a specific band of frequency, which
is used by the services of the astronomy radio under very strict conditions. Therefore, the
standards being applied in the allocation process are set by various bodies including the
European Conference of Postal and Telecommunications Administrations and the International
Telecommunication Union.

COMPUTER SCIENCE 14
While the governments determine the allocation of frequencies at the national level, the
process depends on the collaboration of the governments at the international levels. Importantly,
the service allocations can either be primary or secondary. The former revolves around the
provision of services to the nationally located frequencies while the latter often deals with the
internationally set frequencies.
b. Radio propagation
i. The ionosphere
It is the section of the atmosphere that has been populated or rather receives the full effect of
ionization through the radiations from the sun. The impacts of the solar radiations allow it to play
a critical role in the electricity of the atmospheric section. The electrons available in the
ionosphere determine the radio communication and dictate the directions to be followed by the
radio waves. Therefore, the availability of many electrons in the section facilitates the
transmission of radio frequency across the globe.
ii. Transmitter service
Regarding the fact that some of the nearer regions receive fewer transmissions compared to
the farther regions, the nature of the transmitted signals allow such happenings. At the time of
the transmission, the waves are availed at leave at a higher speed an in a straight line. For that
reason, the rays travel faster to the far regions, leaving the near places with no signal. The
regions depend on the reduced speed of transmission, where the reflections and refractions occur,
allowing the signals to bounce back.
iii. Ionosphere

COMPUTER SCIENCE 15
Apart from the listed factors, the ionosphere is also affected by the density of air circulating
at its lower altitude. The air, which is normally referred to as the populating gas tends to fill the
whole lower region, recombining the ions and the gas molecules. The combination of the two
subjects leads to the introduction of a different layer to the ionosphere, although it will also
depend on solar energy. Finally, the introduction would have changed the state of the ionosphere,
to some given extent.
iv. Propagation Mechanisms
The additional mechanism that waves with lower frequencies possess enabling them to
travel farther is their ability to penetrate solid materials. The earth is full of obstacles, and having
the mandate to penetrate them would mean a big deal to the waves. Besides, the fact that the
waves respond to the reflection that occurs on them through the ionosphere gives them the
advantage to go over long distances. The reason for it is that reflection works better on waves
with lower frequency compared to those with high frequencies.

COMPUTER SCIENCE 16
References
Cheng, M.X., Ruan, L. and Wu, W., 2005. Achieving minimum coverage breach under
bandwidth constraints in wireless sensor networks.
Duffin, R.J. and Schaeffer, A.C., 1952. A class of nonharmonic Fourier series. Transactions of
the American Mathematical Society, 72(2), pp.341-366.
Martin, R., 2001. Noise power spectral density estimation based on optimal smoothing and
minimum statistics. IEEE Transactions on speech and audio processing, 9(5), pp.504-
512.
Martinez, A., I Fabregas, A.G., Caire, G. and Willems, F.M., 2008. Bit-interleaved coded
modulation in the wideband regime. IEEE Transactions on Information Theory, 54(12),
pp.5447-5455.
Ponomarchuk, S., Kotovich, G., Romanova, E. and Tashchilin, A., 2015. Forecasting
characteristics of propagation of decameter radio waves using the global ionosphere and
plasmasphere model. Sollecito-Zemnaya Fizika, 1(3), pp.49-54.
Price, E., and Woodruff, D.P., 2012, July. Applications of the Shannon-hartley theorem to data
streams and sparse recovery. In Information Theory Proceedings (ISIT), 2012 IEEE
International Symposium on (pp. 2446-2450). IEEE.
Raddatz, L., White, I.H., Cunningham, D.G. and Nowell, M.C., 1998. An experimental and
theoretical study of the offset launch technique for the enhancement of the bandwidth of
multimode fiber links. Journal of Lightwave Technology, 16(3), p.324.

COMPUTER SCIENCE 17
Shannon, C.E., 1948. A mathematical theory of communication. Bell system technical
journal, 27(3), pp.379-423.