Numeracy and Data Analysis Report: Train Station Usage Forecasting

This report presents a comprehensive data analysis of train station usage, focusing on Cranbrook station. It begins by organizing the data in a tabular format and visualizing it through column and line charts. The main body delves into descriptive statistics, including the calculation of mean, median, mode, range, and standard deviation, providing step-by-step explanations for each. Furthermore, the report explores the calculation of the 'm' and 'c' values used in linear regression, essential for forecasting. Finally, the report applies these calculations to forecast station usage for 12 and 15 years, offering valuable insights for future planning and decision-making related to station management and resource allocation. The analysis is based on data from 2009-2019 and includes a conclusion summarizing the findings and their implications.

Numeracy and Data Analysis

TABLE OF CONTENTS
INTRODUCTION................................................................................................................................3
MAIN BODY.......................................................................................................................................3
1. Arranging data in a table format...................................................................................................3
2. Presenting dataset using graphical presentation...........................................................................3
3. Computation of descriptive statistics along with the steps...........................................................4
4 (i) Showing steps to calculate m value..........................................................................................7
4 (ii) Presenting steps to assess c value............................................................................................8
4. (iii). Forecasting of station usage for 12 and 15 years.................................................................8
CONCLUSION....................................................................................................................................9
REFERENCES...................................................................................................................................11

INTRODUCTION
Data analysis implies for the process of evaluating numeric figures by using statistical tools
and techniques. In the current times, with the motive to derive suitable information for decision
making companies lay high level of emphasis on undertaking statistical aspects. The present report
will provide deeper insight about total usage of train station dataset. Further, it also entails how
forecasting tools help in making prediction about future.
MAIN BODY

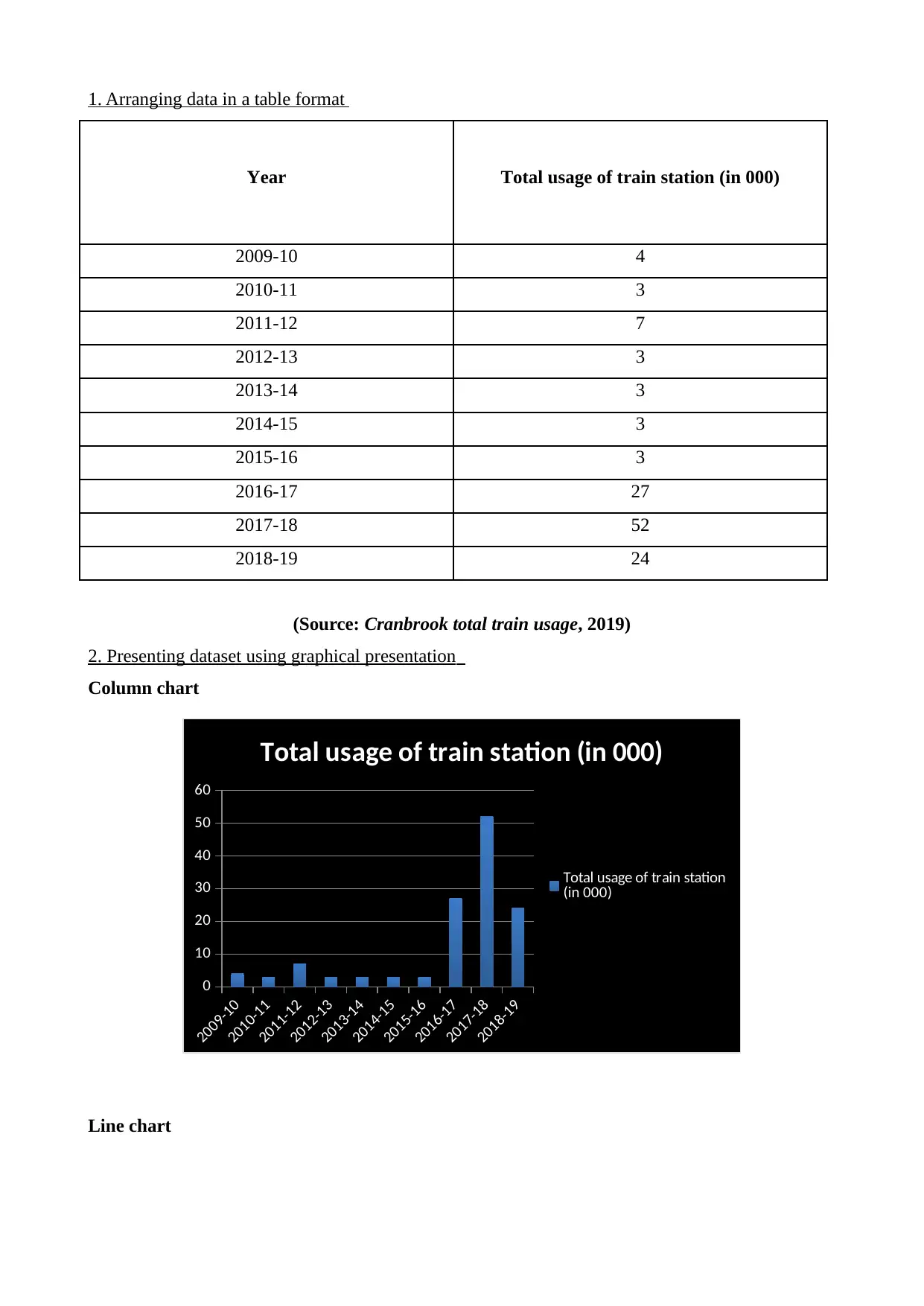
1. Arranging data in a table format
Year Total usage of train station (in 000)
2009-10 4
2010-11 3
2011-12 7
2012-13 3
2013-14 3
2014-15 3
2015-16 3
2016-17 27
2017-18 52
2018-19 24
(Source: Cranbrook total train usage, 2019)
2. Presenting dataset using graphical presentation
Column chart
2009-10
2010-11
2011-12
2012-13
2013-14
2014-15
2015-16
2016-17
2017-18
2018-19
0
10
20
30
40
50
60
Total usage of train station (in 000)
Total usage of train station
(in 000)
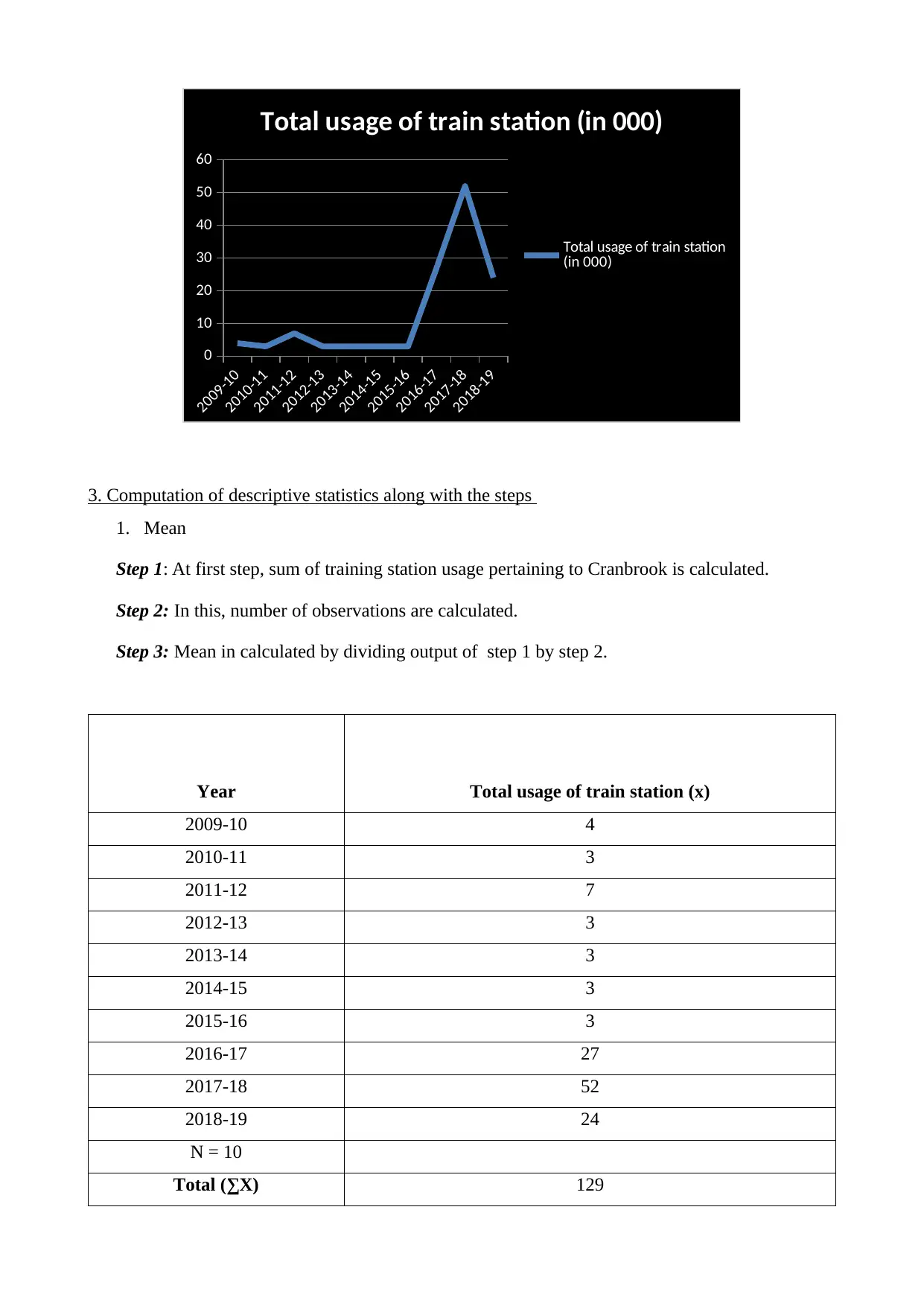
Line chart

2009-10
2010-11
2011-12
2012-13
2013-14
2014-15
2015-16
2016-17
2017-18
2018-19
0
10
20
30
40
50
60
Total usage of train station (in 000)
Total usage of train station
(in 000)
3. Computation of descriptive statistics along with the steps
1. Mean
Step 1: At first step, sum of training station usage pertaining to Cranbrook is calculated.
Step 2: In this, number of observations are calculated.
Step 3: Mean in calculated by dividing output of step 1 by step 2.
Year Total usage of train station (x)
2009-10 4
2010-11 3
2011-12 7
2012-13 3
2013-14 3
2014-15 3
2015-16 3
2016-17 27
2017-18 52
2018-19 24
N = 10
Total (∑X) 129

Mean
∑X ÷ N
129 / 10
= 12.9
Tabular presentation shows that average total usage level accounts for 12.9 (000) respectively.
2. Median
Step 1: Initially, data is arranged in the form of ascending order.
Step 2: Thereafter, following formula is used to assess median value from dataset
M = (N + 1) / 2
Step 3: At this, value of 5th and 6th item is added and divided by 2.
Firstly arranging data set in an ascending order
Year Train usage data set
1 3
2 3
3 3
4 3
5 3
6 4
7 7
8 24
9 27
10 52
Median
(N + 1) / 2
= (10 + 1)/2
= 11 / 2
= 5.5 item
So, (Value of 5th item + value of 6th

item) / 2
= (3 + 4) / 2
= 3.5
3. Mode
Mode = 3
By calculating frequencies value of mode is assessed in individual data series. Outcome of
descriptive statistics shows that value 3 is repeated five times in the year of 2010, 2012, 2013, 2014
& 2015.
4. Range
Particulars Figures
Maximum train usage level 52
Minimum train usage level 3
Range
Maximum – Minimum value
52 – 3
= 49
Step 1: In this, highest value from dataset is calculated.
Step 2: Lowest value of dataset is assessed at step 2.
Step 3: In the last step, minimum value is subtracted from highest figure.
The above depicted table exhibits that maximum and minimum value accounts for 52 & 3
significantly.
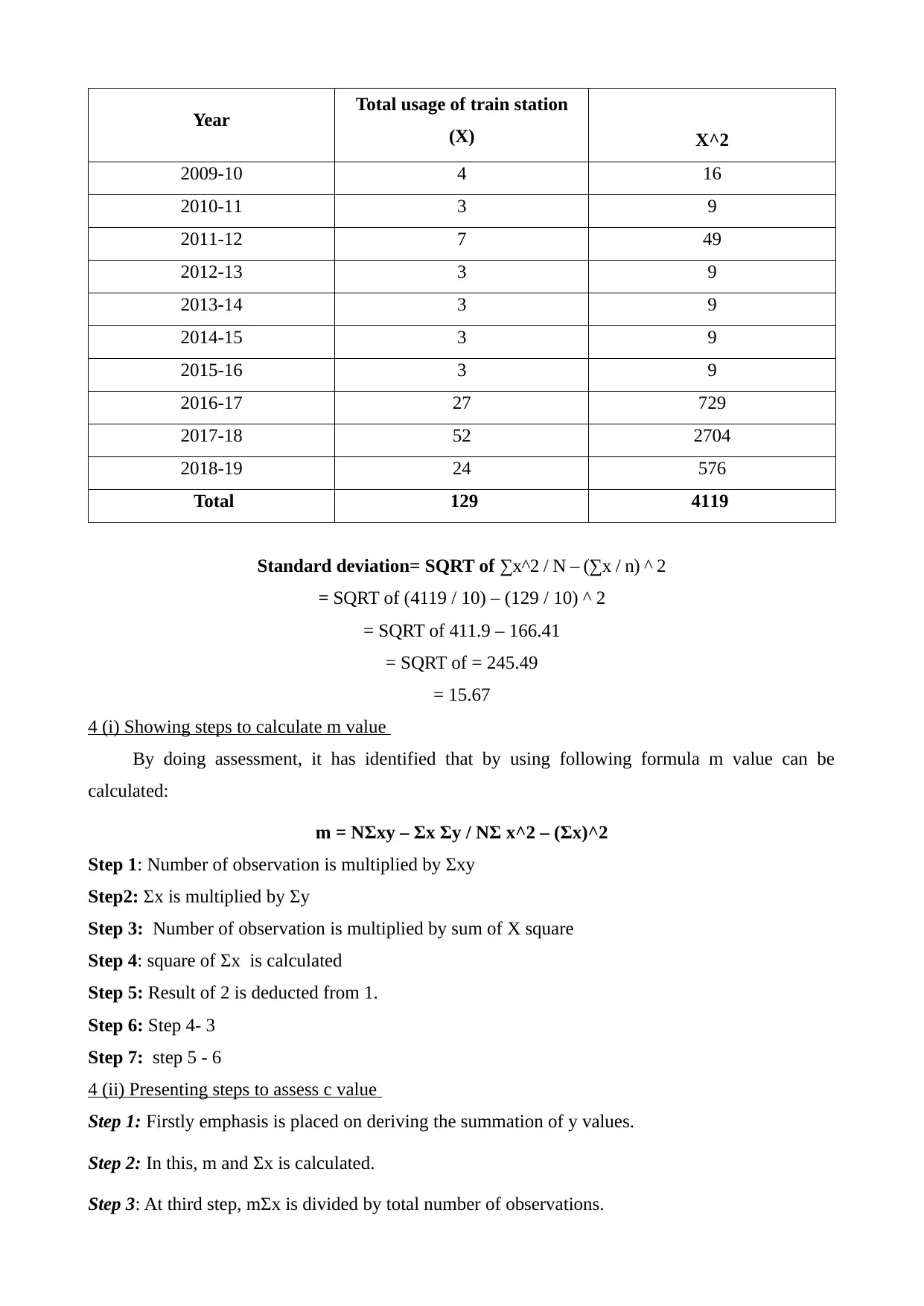
5. Standard deviation
Step 1: Square of all the x values (total usage of train station) is calculated.
Step 2: Thereafter, sum of X^2 is calculated.
Step 3: Results of step 2 is divided from number of observation.
Step 4: Square of ∑x and number of observation is calculated.
Step 5: For calculating variance below mentioned formula is used.
∑x^2 / N – (∑x / n) ^ 2
Step 6: Square root of variance is calculated for assessing standard deviation.

Year Total usage of train station
(X) X^2
2009-10 4 16
2010-11 3 9
2011-12 7 49
2012-13 3 9
2013-14 3 9
2014-15 3 9
2015-16 3 9
2016-17 27 729
2017-18 52 2704
2018-19 24 576
Total 129 4119
Standard deviation= SQRT of ∑x^2 / N – (∑x / n) ^ 2
= SQRT of (4119 / 10) – (129 / 10) ^ 2
= SQRT of 411.9 – 166.41
= SQRT of = 245.49
= 15.67
4 (i) Showing steps to calculate m value
By doing assessment, it has identified that by using following formula m value can be
calculated:
m = NΣxy – Σx Σy / NΣ x^2 – (Σx)^2
Step 1: Number of observation is multiplied by Σxy
Step2: Σx is multiplied by Σy
Step 3: Number of observation is multiplied by sum of X square
Step 4: square of Σx is calculated
Step 5: Result of 2 is deducted from 1.
Step 6: Step 4- 3
Step 7: step 5 - 6
4 (ii) Presenting steps to assess c value
Step 1: Firstly emphasis is placed on deriving the summation of y values.
Step 2: In this, m and Σx is calculated.
Step 3: At third step, mΣx is divided by total number of observations.

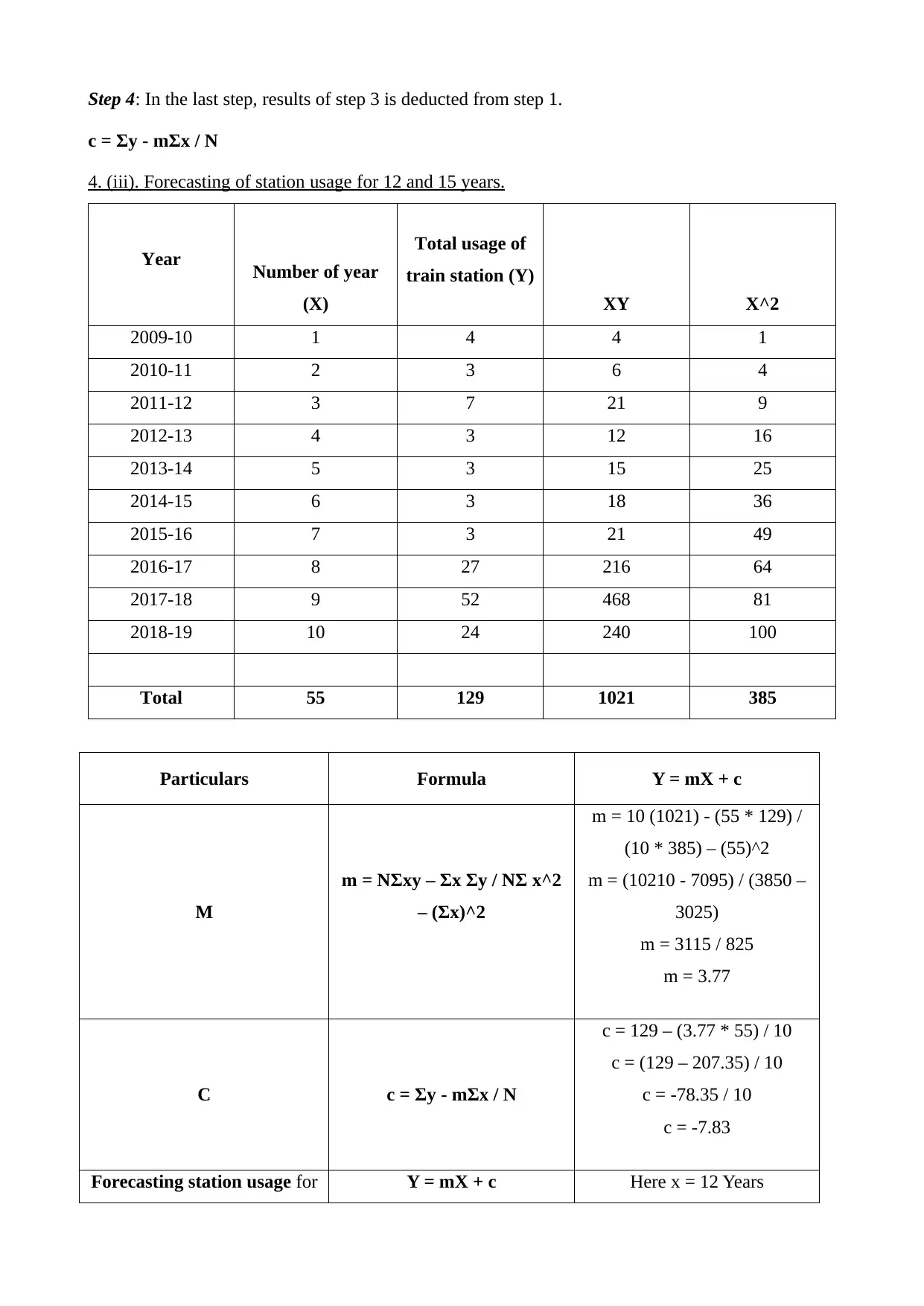
Step 4: In the last step, results of step 3 is deducted from step 1.
c = Σy - mΣx / N
4. (iii). Forecasting of station usage for 12 and 15 years.
Year Number of year
(X)
Total usage of
train station (Y)
XY X^2
2009-10 1 4 4 1
2010-11 2 3 6 4
2011-12 3 7 21 9
2012-13 4 3 12 16
2013-14 5 3 15 25
2014-15 6 3 18 36
2015-16 7 3 21 49
2016-17 8 27 216 64
2017-18 9 52 468 81
2018-19 10 24 240 100
Total 55 129 1021 385
Particulars Formula Y = mX + c
M
m = NΣxy – Σx Σy / NΣ x^2
– (Σx)^2
m = 10 (1021) - (55 * 129) /
(10 * 385) – (55)^2
m = (10210 - 7095) / (3850 –
3025)
m = 3115 / 825
m = 3.77
C c = Σy - mΣx / N
c = 129 – (3.77 * 55) / 10
c = (129 – 207.35) / 10
c = -78.35 / 10
c = -7.83
Forecasting station usage for Y = mX + c Here x = 12 Years

12 year Y = 3.77 (12) + (-7.83)
Y = 45.24 – 7.83
Y = 37.41
Forecasting for 15 year
Y = mX + c Here x = 15 Years
Y = 3.77 (15) + (-7.83)
Y = 56.55 – 7.83
Y = 48.72
CONCLUSION
By summing up this report, it can be concluded that descriptive statistical tool helps in
summarizing gathered data set effectually. Besides this, it can be inferred that in the year of 12 &
15 total usage of Cranbrook station will be 37.41 and 48.72 respectively. Hence, such statistical tool
helps in make effectual decision regarding Cranbrook station.

REFERENCES
Online
Cranbrook total train usage. 2019. [Online]. Available through: <
https://orr.gov.uk/statistics/published-stats/station-usage-estimates >.