Operation Research: North West Corner Rule for Transportation Problem

This assignment focuses on solving a transportation problem using the North West Corner Rule method. The problem involves a construction company in Riyadh, Saudi Arabia, aiming to minimize the cost of transporting concrete from five depots to twelve construction sites. The report details the application of the North West Corner Rule to develop a first feasible solution, determining the optimal allocation of concrete from each depot to meet the demands of the construction sites. The solution finds a minimum transportation cost of 12,840 SAR. The assignment further validates the solution by confirming that the number of allocations meets the criteria for a non-degenerate solution, ensuring its viability. Desklib provides a platform to access this and similar solved assignments for students' reference and learning.

North West Corner Rule Method 1
NORTH WEST CORNER RULE METHOD
Name
Course
Professor
University
City/state
Date

North West Corner Rule Method 2
Table of Contents
Abstract......................................................................................................................................................3
Summary of results....................................................................................................................................3
The problem...............................................................................................................................................3
North-west corner rule method................................................................................................................4
References..................................................................................................................................................7

North West Corner Rule Method 3
Abstract
The purpose of this report is to develop a first feasible solution that will ensure that a Riyadh-
based construction company incurs the least cost to transport the required volume of concrete
from five depots to the 12 construction sites located in 12 different cities across Saudi Arabia.
The total demand of concrete is 2,000m3, which equals the total supply. North-west corner rule
has been used to solve this transportation problem. The first feasible solution developed show
that the least amount of money that the company will use for transportation is 12,840 SAR.
Summary of results
The five depots have the capacity to supply 2,000 m3 of ready-mixed concrete and the
company’s demand is 2,000m3 hence demand equals supply. The minimum transportation cost
for the company to supply all the 12 construction sites with the required volume of concrete from
the five depots s 12,840 SAR. The first feasible solution developed in this report is non-
degenerate because the number of allocations in the north-west corner rule table is equal to the m
(no. of rows) + n (no. of columns) – 1.
The problem
A construction company based in Riyadh, Saudi Arabia has 12 ongoing construction
projects in 12 different cities in the country. The company has identified five depots P, Q, R, S
and T, and is planning to supply ready-mixed concrete from these depots to the 12 construction
sites. The volume of concrete (in m3) that each depot can supply, the volume of concrete (in m3)
that each site requires, and the transportation cost (in SAR) of one volume of concrete (in m3)
from each depot to each construction site are provided in the table below. The company wants a
first feasible solution that will ensure that it uses the lowest cost possible to transport the required
concrete from the five depots to all the 12 construction sites.

North West Corner Rule Method 4
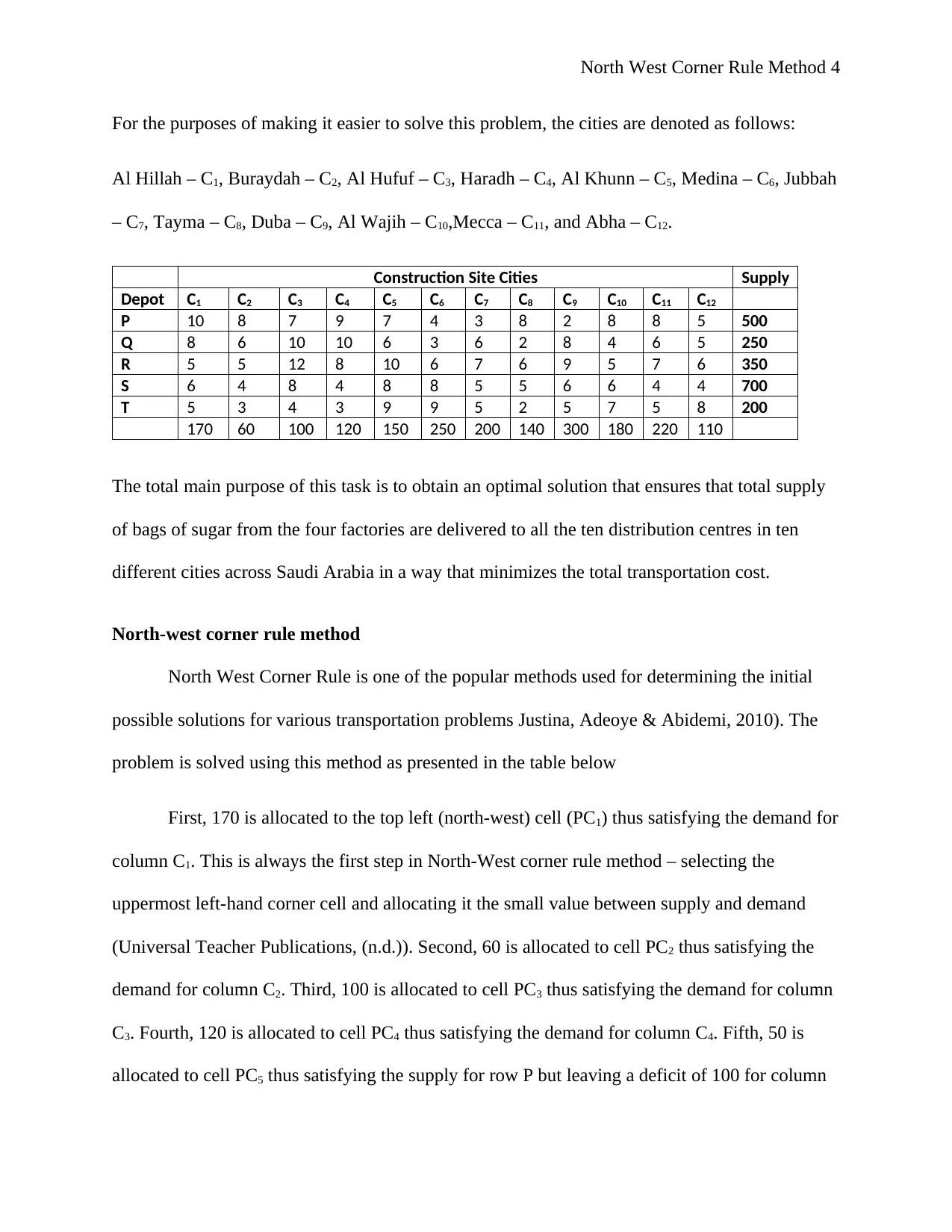
For the purposes of making it easier to solve this problem, the cities are denoted as follows:
Al Hillah – C1, Buraydah – C2, Al Hufuf – C3, Haradh – C4, Al Khunn – C5, Medina – C6, Jubbah
– C7, Tayma – C8, Duba – C9, Al Wajih – C10,Mecca – C11, and Abha – C12.
Construction Site Cities Supply
Depot C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
P 10 8 7 9 7 4 3 8 2 8 8 5 500
Q 8 6 10 10 6 3 6 2 8 4 6 5 250
R 5 5 12 8 10 6 7 6 9 5 7 6 350
S 6 4 8 4 8 8 5 5 6 6 4 4 700
T 5 3 4 3 9 9 5 2 5 7 5 8 200
170 60 100 120 150 250 200 140 300 180 220 110
The total main purpose of this task is to obtain an optimal solution that ensures that total supply
of bags of sugar from the four factories are delivered to all the ten distribution centres in ten
different cities across Saudi Arabia in a way that minimizes the total transportation cost.
North-west corner rule method
North West Corner Rule is one of the popular methods used for determining the initial
possible solutions for various transportation problems Justina, Adeoye & Abidemi, 2010). The
problem is solved using this method as presented in the table below
First, 170 is allocated to the top left (north-west) cell (PC1) thus satisfying the demand for
column C1. This is always the first step in North-West corner rule method – selecting the
uppermost left-hand corner cell and allocating it the small value between supply and demand
(Universal Teacher Publications, (n.d.)). Second, 60 is allocated to cell PC2 thus satisfying the
demand for column C2. Third, 100 is allocated to cell PC3 thus satisfying the demand for column
C3. Fourth, 120 is allocated to cell PC4 thus satisfying the demand for column C4. Fifth, 50 is
allocated to cell PC5 thus satisfying the supply for row P but leaving a deficit of 100 for column

North West Corner Rule Method 5
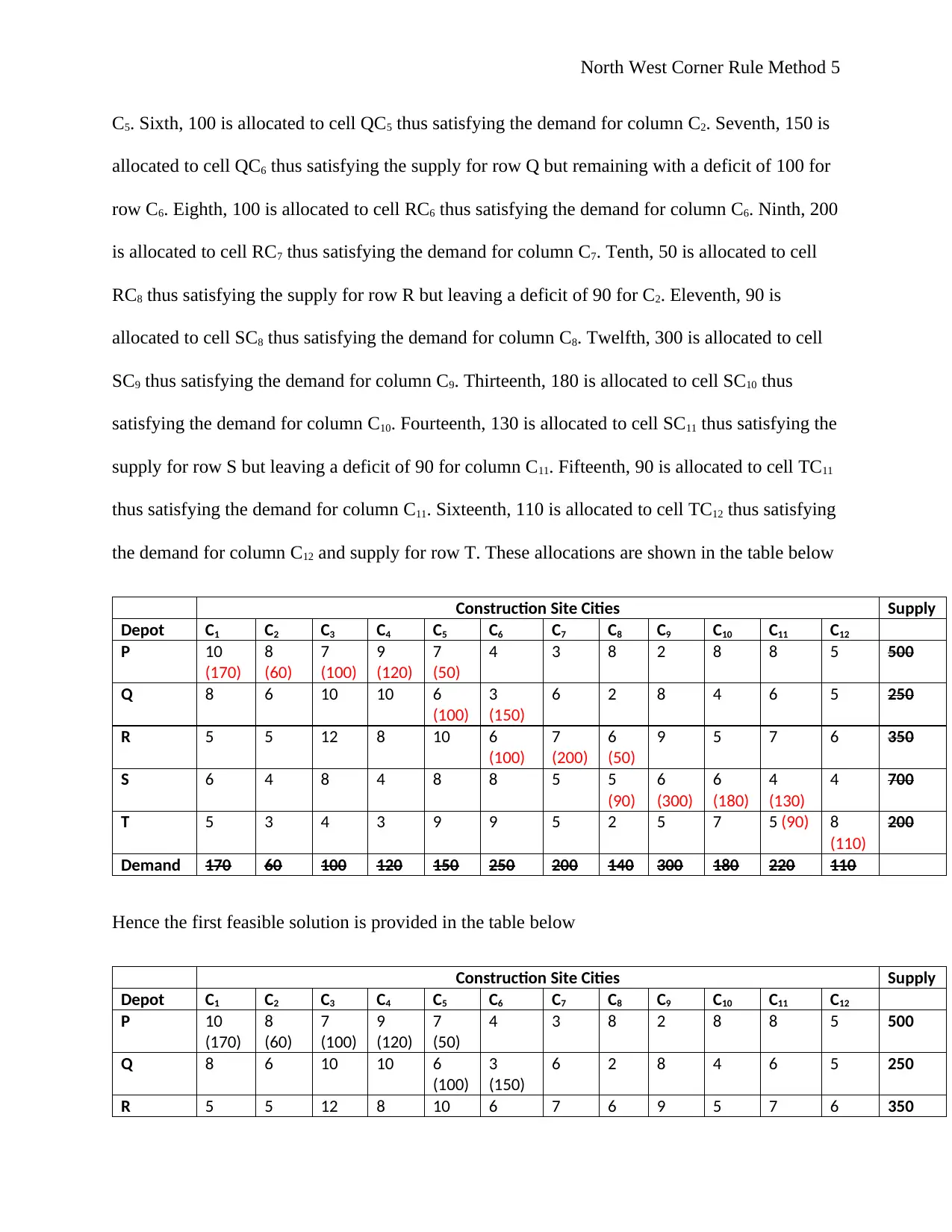
C5. Sixth, 100 is allocated to cell QC5 thus satisfying the demand for column C2. Seventh, 150 is
allocated to cell QC6 thus satisfying the supply for row Q but remaining with a deficit of 100 for
row C6. Eighth, 100 is allocated to cell RC6 thus satisfying the demand for column C6. Ninth, 200
is allocated to cell RC7 thus satisfying the demand for column C7. Tenth, 50 is allocated to cell
RC8 thus satisfying the supply for row R but leaving a deficit of 90 for C2. Eleventh, 90 is
allocated to cell SC8 thus satisfying the demand for column C8. Twelfth, 300 is allocated to cell
SC9 thus satisfying the demand for column C9. Thirteenth, 180 is allocated to cell SC10 thus
satisfying the demand for column C10. Fourteenth, 130 is allocated to cell SC11 thus satisfying the
supply for row S but leaving a deficit of 90 for column C11. Fifteenth, 90 is allocated to cell TC11
thus satisfying the demand for column C11. Sixteenth, 110 is allocated to cell TC12 thus satisfying
the demand for column C12 and supply for row T. These allocations are shown in the table below
Construction Site Cities Supply
Depot C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
P 10
(170)
8
(60)
7
(100)
9
(120)
7
(50)
4 3 8 2 8 8 5 500
Q 8 6 10 10 6
(100)
3
(150)
6 2 8 4 6 5 250
R 5 5 12 8 10 6
(100)
7
(200)
6
(50)
9 5 7 6 350
S 6 4 8 4 8 8 5 5
(90)
6
(300)
6
(180)
4
(130)
4 700
T 5 3 4 3 9 9 5 2 5 7 5 (90) 8
(110)
200
Demand 170 60 100 120 150 250 200 140 300 180 220 110
Hence the first feasible solution is provided in the table below
Construction Site Cities Supply
Depot C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
P 10
(170)
8
(60)
7
(100)
9
(120)
7
(50)
4 3 8 2 8 8 5 500
Q 8 6 10 10 6
(100)
3
(150)
6 2 8 4 6 5 250
R 5 5 12 8 10 6 7 6 9 5 7 6 350

North West Corner Rule Method 6
(100) (200) (50)
S 6 4 8 4 8 8 5 5
(90)
6
(300)
6
(180)
4
(130)
4 700
T 5 3 4 3 9 9 5 2 5 7 5 (90) 8
(110)
200
Demand 170 60 100 120 150 250 200 140 300 180 220 110
Total demand = 2,000 m3 of concrete
Total supply = 2,000 m3 of concrete
Hence total demand = total supply
The total cost of transportation is calculated from the table above using the formula∑
i=1
N
DiCi;
where i = particular construction site, N = total number of construction sites, Di = concrete
demand for a particular construction site, and Ci = transportation cost per unit volume of concrete
from a particular depot to a specific site (Klinz & Woeginger, 2011).
According to the first feasible solution, the total minimum cost of transporting the 2,000m3 of
concrete from the five depots to the 12 construction sites is:
= (10 x 170) + (8 x 60) + (7 x 100) + (9 x 120) + (7 x 50) + (6 x 100) + (3 x 150) + (6 x 100) + (7
x 200) + (6 x 50) + (5 x 90) + (6 x 300) + (6 x 180) + (4 x 130) + (5 x 90) + (8 x 110)
= 1,700 + 480 + 700 + 1,080 + 350 + 600 + 450 + 600 + 1,400 + 300 + 450 + 1,800 + 1,080 +
520 + 450 + 880
= 12,840 SAR
Total minimum transportation cost
Number of cells with allocations = 16

North West Corner Rule Method 7
Number of basic variables according to north west corner rule method = m + n – 1
m = number of rows = 5
n = number of columns = 12
Hence number of basic variables = 5 + 12 – 1 = 16
This means that the initial possible solution obtained for the transportation problem is non-
degenerate (it is the first best solution that the company should use).
References
Justina, A. E., Adeoye, A. O. & Abidemi, T. F., 2010. Comparison of Statistical Packages in Solving
Transportation Problems. International Journal of Advanced Research in Computer science, 4(10), pp. 97-
102.
Klinz, B. & Woeginger, G., 2011. The Northwest corner rule revisited.. Discrete Applied Mathematics,
159(12), pp. 1284-1289.
Universal Teacher Publications, (n.d.). North West Corner Rule. [Online]
Available at: http://www.universalteacherpublications.com/univ/ebooks/or/ch5/nw.htm
[Accessed 24 November 2018].