Analysis of the Travelling Salesman Problem and its Applications

This report provides a comprehensive analysis of the Travelling Salesman Problem (TSP), a fundamental problem in discrete mathematics and computer science. It begins with a problem definition, explaining the core concept of finding the most efficient route between multiple locations. The report then explores various real-world applications of the TSP, including logistics, supply chain management, and the manufacturing of microchips. It highlights how businesses utilize TSP to optimize routes, minimize costs, and improve efficiency. The report delves into different solution methods, such as the Hungarian method and the branch and bound (B&B) method, with a detailed example of how B&B can be applied to solve the problem. Furthermore, it discusses possible algorithms used in computer applications and logistics, emphasizing the role of the branch and bound algorithm in optimization. The conclusion summarizes the importance of TSP in academics and practical applications, emphasizing its role in cost, quality, and time savings. The report also includes a short statement reflecting on the learning experience and challenges faced during the analysis.

Discreet Mathematics

TABLE OF CONTENTS
INTRODUCTION ..........................................................................................................................1
PROBLEM DEFINITION ..............................................................................................................1
APPLICATIONS OF TRAVELLING SALESMAN PROBLEM IN REAL WORLD..................1
SOLUTIONS ..................................................................................................................................2
POSSIBLE ALGORITHMS ...........................................................................................................5
CONCLUSION ...............................................................................................................................6
SHORT STATEMENT ...................................................................................................................7
REFERENCES ...............................................................................................................................8

INTRODUCTION
The mathematical concepts such as geometry, measurements, logics and statistics are
widely used in real world applications. These concepts play significant role in academics and
research but their application in dealing with practical life situations is also one of the popular
trend (Kyritsis and et.al., 2017). The report will analyse one such problem named travelling
salesman problem (TSP) and its practical applications. It will also explain the available solution
methods and algorithms for solving the problem.
PROBLEM DEFINITION
TSP is one of the most popular algorithm based problem which helps to determine the
optimum or most efficient route possible between given set of locations and distances. Usually in
its problem statement different locations or points are given and an individual is required to
travel between two points by taking the shortest possible path so that time, distance and cost can
be saved. Thus the problem is widely used by the business organisations in their supply chain
management (Ouaarab, Ahiod and Yang, 2015). TSP consist of large number of variables and
thus it is very complex to solve these problems. The problem definition can be given as follows:
An individual or salesman is required to travel to certain destinations. The salesman is
required to cover each location exactly at once and must follow the shortest path. Every
destination is represented as vertex and path between two vertices is represented as its edge. The
problem can be interpreted to all the applications which requires the analysis of shortest or the
longest paths between two destinations (Hazra and Hore, 2016).
APPLICATIONS OF TRAVELLING SALESMAN PROBLEM IN REAL
WORLD
The TSP finds a wide range of applications in various fields. In its simplest form it is
used in planning, logistic and supply chain of operational management process of business
organisations as well as in manufacturing of microchips which requires the analysis of shortest
paths. In the applications associated with the travelling it is used as an essential tool to determine
the shortest path (Salazar-González and Santos-Hernández, 2015). Being an optimization
problem it is also used in computer applications which requires the data transmission between
nodes through minimum distance.
1

Thus in logistic, packaging and scheduling of the objects TSP provides the effective
solutions. The problem is also used for accomplishing tasks such as computer wiring, production
of printed circuit boards and routing problems which requires the analysis of the shortest path.
The supply chain network of the organisations includes customers and suppliers which are
located at diverse locations. Thus if supply chain path is not planned properly by the
organisations then it can lead to increment in distribution time, cost and distance.
For determining the shortest geographical routes business organisations apply TSP in
their operational procedures. Similarly while defining networks or data transfer path in
computers and manufacturing of PCB the time delay can be increased if wiring paths are not
optimized (Bhatt and et.al., 2017). Thus during their manufacturing process special attention is
paid to the designing process to assure that between different connecting points or nodes shortest
path is maintained. This analysis is not possible without solving TSP.
SOLUTIONS
The TSP can be solved by using various methods such as Hungarian method, branch and
bound method (B&B) and one's assignment method. However B&B can be considered as one of
the effective way to find the optimum solution for the problem. B&B techniques can be applied
to the problems which cannot be solved by the dynamic programming and greedy method.
Though number of iterations can lead make this solution much slower in worst cases but if it is
applied carefully then it can provide optimum solution fast (Cvetković and et.al., 2018).
This method is based on the concept that the problem is divided into sub problems and then for
each of the sub problem solutions are determined. An example of TSP solution by using B&B is
provided as follows:
A salesman has to start his journey from city A to cities B, C and D. The cost of travelling
between these cities is given in figure below. The optimum path which must be covered to give
minimum cost is determined by applying B&B.
2

1) At first initial cost matrix is formed and is reduced.
A B C D
A - 4 12 7
B 5 - - 18
C 11 - - 6
D 10 2 3 -
2). In next step a minimum value is selected from each row and then it is subtracted from each
row element. This procedure is followed with all rows and the resultant matrix is called row
reduced matrix which is :
Row reduced matrix:
A B C D
A - 0 8 3
B 0 - - 13
C 5 - - 0
D 8 0 1 -
3

3). Similarly column reduced matrix is obtained by using minimum value in each column. Since
column 1, 2 and 4 already consist of a zero there is no need to reduce them and thus only column
3 is reduced.
Column reduced matrix:
A B C D
A - 0 7 3
B 0 - - 13
C 5 - - 0
D 8 0 0 -
The cost of node 1 is equals to sum of minimum row values used in step 2 and minimum column
values used in step 3. Thus its cost is given as C1
C1= 4+ 5+ 6+ 2 +1 = 18
4.) In this step all other cities are considered to which salesman can travel from A city.
A to B
Cost of going from A to B = C(AB) = 0 [Cost taken from reduced matrix of step 3]
Row A and column = -
Cost of going from B to A = -
Thus resulting cost matrix is given as follows:
A B C D
A - - - -
B - - - 13
C 5 - - 0
D 8 - 0 -
4

After performing row and column reduction of this matrix following matrix is obtained:
A B C D
A - - - -
B - - - 0
C 0 - - 0
D 3 - 0 -
Cost of node 2 = C2 = C1 + Sum of reduction elements + C(AB)
C2 = 18 + (13+5) +0 = 36
In the similar manner the cost of going from node A to node C and node D are also calculated.
Thus we obtain:
C2 = 36 (For path A to B)
C3 = 25 (For path A to C)
C4 = 26 (For path A to D)
The lowest cost is for path C thus for minimum cost salesman must travel from city A to city C.
Now from city C (node 3) salesman can go to either city B or city D. For this purpose the cost
matrix at node 3 is used that is the matrix generated while travelling from A to C. The matrix is
reduced in the similar manner as in the stages described above and finally optimum path from
second destination C can also be analysed.
POSSIBLE ALGORITHMS
The most wide use of TSP is in logistic and in computer applications. For this purpose
these applications uses branch and bound algorithms so that optimization problems in logistic
and computer applications can be solved (Benavent and et.al., 2019). In this algorithm all
possible tours which are performed by the salesman between different locations are divided into
5

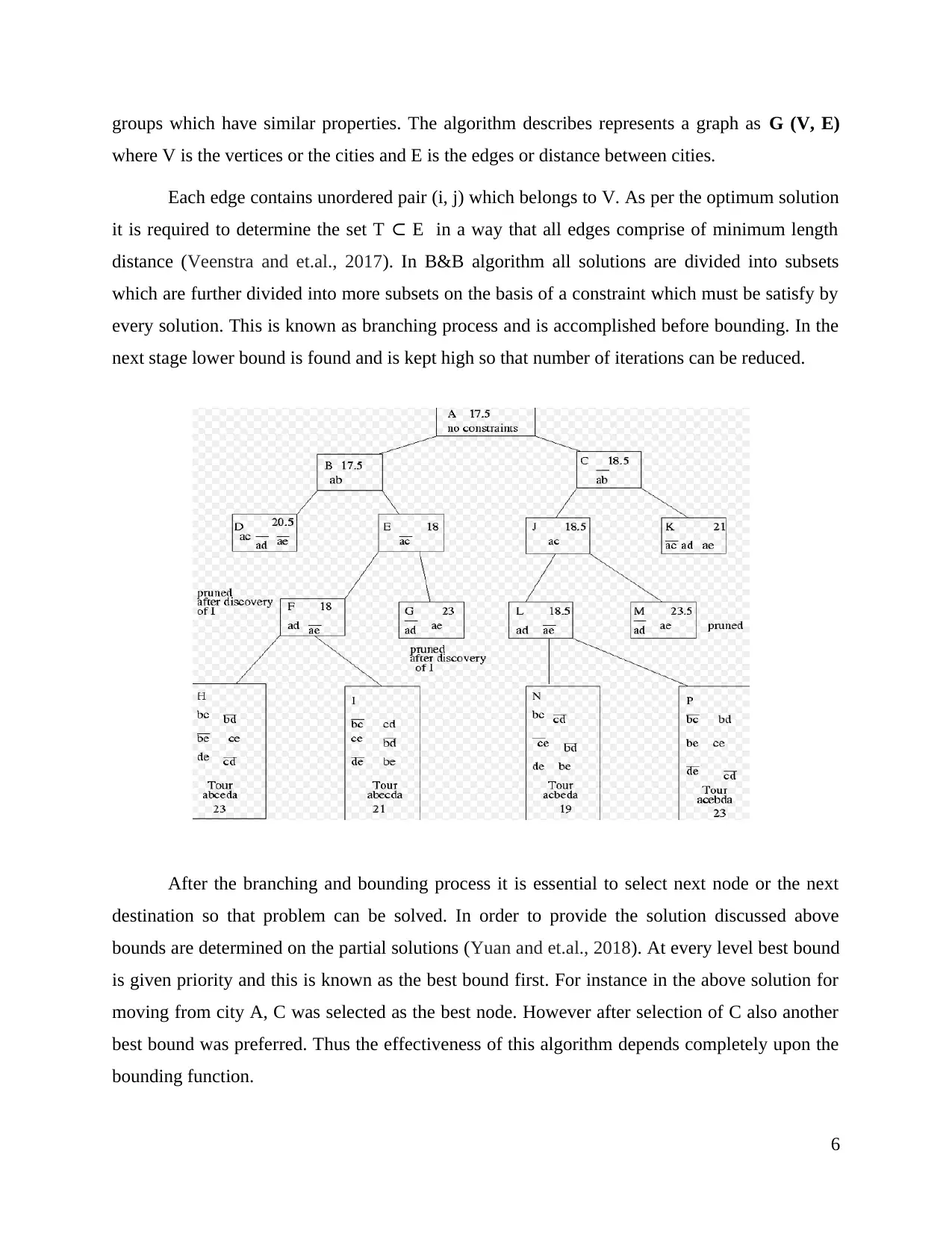
groups which have similar properties. The algorithm describes represents a graph as G (V, E)
where V is the vertices or the cities and E is the edges or distance between cities.
Each edge contains unordered pair (i, j) which belongs to V. As per the optimum solution
it is required to determine the set T E in a way that all edges comprise of minimum length⊂
distance (Veenstra and et.al., 2017). In B&B algorithm all solutions are divided into subsets
which are further divided into more subsets on the basis of a constraint which must be satisfy by
every solution. This is known as branching process and is accomplished before bounding. In the
next stage lower bound is found and is kept high so that number of iterations can be reduced.
After the branching and bounding process it is essential to select next node or the next
destination so that problem can be solved. In order to provide the solution discussed above
bounds are determined on the partial solutions (Yuan and et.al., 2018). At every level best bound
is given priority and this is known as the best bound first. For instance in the above solution for
moving from city A, C was selected as the best node. However after selection of C also another
best bound was preferred. Thus the effectiveness of this algorithm depends completely upon the
bounding function.
6

CONCLUSION
It can be concluded from the report that travelling salesman problem not only find its
application in academics but is also used widely in business processes as well as computer
applications. It has been also analysed from the study that the better understanding of TSP
algorithms and solution methods can help individuals to make their processes more effective in
terms of cost, quality and time saving perspective. The report has explained the different
solutions, detailed applications of the problem and role of computing techniques to solve the
problem. From the above discussion it can also be concluded that such mathematical analysis can
be helpful in exploring the use of mathematics in practical applications.
SHORT STATEMENT
The analysis of mathematical model has been very beneficial for me as it helped to
understand that how maths problems are used in real life. The study helped me to develop better
understanding of TSP and how it can make logistic process easy. Initially it was very hard and
complex to formulate the problem in the form of mathematical equation. Thus I was not sure that
if if will be possible to formulate this problem into real world application or not. Since I was
working in team there were many instances when it was not able to reach a final conclusion.
For example when we were searching for the different solution methods and algorithms
then each of team member has different opinion. However we tried to understand and compare
various algorithms and reached to the conclusions that which method will be best suitable for
solving problem. During modelling we also found that there are vast number of algorithms which
can provide solution with minimum errors and less number of iterations. In my opinion the
model used by us can be the basic model analysis and in future we can explore this to more
complex models.
7

REFERENCES
Books and Journals
Kyritsis, M. and et.al., 2017. Sense of direction and conscientiousness as predictors of
performance in the Euclidean travelling salesman problem.Heliyon. 3(11). p.e00461.
Ouaarab, A., Ahiod, B. and Yang, X.S., 2015. Random-key cuckoo search for the travelling
salesman problem. Soft Computing. 19(4). pp.1099-1106.
Salazar-González, J.J. and Santos-Hernández, B., 2015. The split-demand one-commodity
pickup-and-delivery travelling salesman problem. Transportation Research Part B:
Methodological. 75. pp.58-73.
Yuan, Y. and et.al., 2018, February. A branch-and-cut algorithm for the generalized traveling
salesman problem with time windows. In ROADEF 2018-19ème Congrès Annuel de la
Société Française de Recherche Opérationnelle et d’Aide à la Décision, Feb 2018.
Veenstra, M. and et.al., 2017. The pickup and delivery traveling salesman problem with handling
costs. European Journal of Operational Research. 257(1). pp.118-132.
Benavent, E. and et.al., 2019. The probabilistic pickup-and-delivery travelling salesman
problem. Expert Systems with Applications. 121. pp.313-323.
Cvetković, D. and et.al., 2018. Complexity indices for the traveling salesman problem based on
short edge subgraphs. Central European Journal of Operations Research. 26(3). pp.759-
769.
Bhatt, S.H. and et.al., 2017. Review on Branch and Bound technique in Flexible Manufacturing
System Scheduling.
Hazra, T.K. and Hore, A., 2016, October. A comparative study of Travelling Salesman Problem
and solution using different algorithm design techniques. In Information Technology,
Electronics and Mobile Communication Conference (IEMCON), 2016 IEEE 7th
Annual (pp. 1-7). IEEE.
8

9