TSP Model Solution: Integer Linear Programming for Salesperson Problem

This assignment provides a comprehensive solution to the Traveling Salesperson Problem (TSP) using the Integer Linear Programming (ILP) model. It begins with an introduction to the TSP, explaining its significance and applications, particularly in supply chain optimization. The solution demonstrates the ILP model's application through a bread distribution example, calculating the shortest distance for a distributor visiting multiple shops. The assignment also includes a literature review, analyzing various research papers that explore the TSP and ILP models in different contexts, such as vehicle routing, maritime search and rescue, and logistic practices. The similarities and differences between the articles are discussed, along with the limitations of the TSP model. This assignment provides a detailed understanding of the TSP, its solution using ILP, and its relevance in business development and supply chain management.

STP Model 1
TSP MODEL
by Student’s Name
Code + Course Name
Professor’s Name
University Name
City, State
Date

STP Model 2
TSP Model
Step one: Identification and solution of a typical problem
1.1 Background
The Traveling Salesperson Problem refers to the challenge of determining the shortest
routes that visit a given set of customers in an area and returns to the initial starting point. The
TSP was formulated or the first time in the year 1930 and is ranked among the most intensive
problems that are studied when it comes to optimization (Brucato 2013). The problem of TPS is
considered very difficult by many people, although there are a number of exact algorithms and
heuristics that have been coined to help in the provision of its solution. The heuristics and
algorithms have been highly instrumental in helping salesmen to solve traveling problems when
they have very many cities to consider (Stanek, Greistorfer, Ladner and Pferschy 2018). The TSP
has, however, proved to be highly instrumental and effective because it has many applications
even when considered in its purest formulation. For instance, it is applicable in logistics,
planning, and also the manufacturing process of microchips (Matai, Singh, and Mittal 2010).
After slight modification, the TSP also qualifies as a sub-problem in other fields of application,
such as DNA sequencing and astronomy (Mo and Xu 2010). Thus the TPS is a critical problem
that is important to understand and advance combinatory optimization problems.
1.2 Model
The proposed model for the Travelling Salesperson Problem (TSP) is the Integer Linear
Programming (ILP) model. The Integer Linear Programing model is a feasibility program, or
mathematical optimization programs where all the variables that are applied are utilized are
restricted to be integers (Ganian, and Ordyniak 2019). The other constraints apart from the
integer constraints in the ILP model and the objective functions are linear. The ILP model is

STP Model 3
particularly used to solve problems in various areas such as vehicle routing, process scheduling,
network hub location, and packaging, among other areas (Pferschy and Staněk 2017). It is thus a
highly effective model that makes it very relevant in addressing the traveling Salesperson
Problem. One unique feature of the ILP model that makes it perfect for the Travelling
Salesperson Problem is that it is NP-complete (Vali and Salimifard 2017). Currently, many
scholars have invested time in understanding and advancing the model more to enhance its
performance. Some of the aspects regarding the model that have been better understood in
contemporary times include restrictions of the number of variables or constraints (Salvador
2010). One of the notable scholarly advancement of the ILP model in the recent past has been the
carried out is the systematic study of the sophistication of ILP through the view of variable
constraints interaction (Ganian and Ordyniak 2019).
In the ILP model, the decision variables, which are a representation of the solution of the
problem, are represented by mathematical symbols. The constraints, the operational
requirements, and the strategic business requirements are modeled using a linear combination of
decision variables in the ILP model (Wiener and Tenbrink 2008). The ILP model utilizes the
objective function, which is a special linear combination of decision variables to model the
specific aspect that the business aims to optimize. The objective functions are optimized in the
ILP model using solutions of inequalities and equations which are obtained using ILP solvers
such as FICO XpressMP (Carroll and Keenan 2019). In the ILP model, the constraints can be
referred to as the limitations that exist on the decision variable. The constraints in the ILP model
are important considerations because they play the role of limiting the decision variables. The
ILP model is, therefore, a good model that can be applied in addressing the TSP (Margot 2010).

STP Model 4
1.3 Solving an example
USING THE ILP (INTEGER LINEAR PROGRAMMING) MODEL
Example
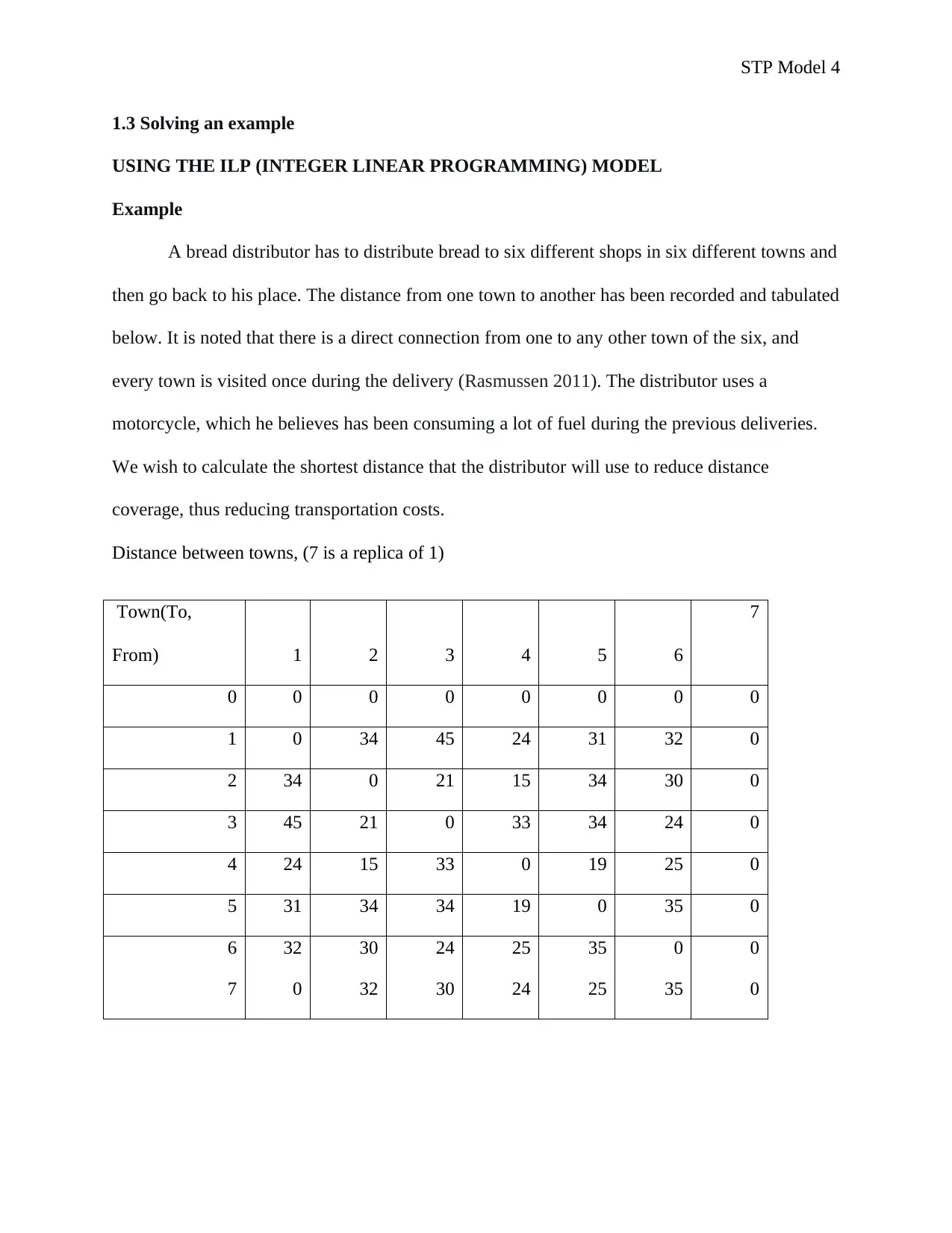
A bread distributor has to distribute bread to six different shops in six different towns and
then go back to his place. The distance from one town to another has been recorded and tabulated
below. It is noted that there is a direct connection from one to any other town of the six, and
every town is visited once during the delivery (Rasmussen 2011). The distributor uses a
motorcycle, which he believes has been consuming a lot of fuel during the previous deliveries.
We wish to calculate the shortest distance that the distributor will use to reduce distance
coverage, thus reducing transportation costs.
Distance between towns, (7 is a replica of 1)
Town(To,
From) 1 2 3 4 5 6
7
0 0 0 0 0 0 0 0
1 0 34 45 24 31 32 0
2 34 0 21 15 34 30 0
3 45 21 0 33 34 24 0
4 24 15 33 0 19 25 0
5 31 34 34 19 0 35 0
6 32 30 24 25 35 0 0
7 0 32 30 24 25 35 0

STP Model 5
SOLUTION:
i. We set the variables as, N (the size) = 6 towns and the arcs (the distance) =
A={(i,j):i,j∈N,i ≠ j},
ii. we then seek to find a linear combination that minimizes the distance covered using
the optimization formula of an excel solver as shown below;

STP Model 6
In the above excel, the explained operations are as summarized below;
Cell Formula Copied to Operation done
F5 =SUM(B21:G21) SUM of the
minimum path
distance
B18 =INDEX($B$9:G$14,B17,C17) B18:G18 Defining the paths
B21 =INDEX($B$9:$G$14,B20,C20
)
B21:G21 Finding the
minimum path.
The results show that the minimum path will be N (6, 3, 2, 4, 5, 1) with the distance sequence
equal A(24, 21,15,19,31,32), which has a distance sum of 142. This implies that the distributor
should start from market 6, then 3, 2, 4, 5, and lastly 1 to reduce the transport costs.
Step 2: Literature Review
Many advancements have been made in the Integer Linear Programming model to
enhance its effectiveness in various areas of application, such as vehicle routing to address the
traveling Salesperson Problem. There are a number of instrumental articles that have addressed
various knowledge gaps in the field of the supply chain. The literature review is going to exploit
various aspects of the literature identified and explain some of the ways that they have helped to
address the knowledge gaps and improve the application of the ILP in addressing TSP. The five
articles include:
1. “Solving Integer Linear Programs by Exploiting Variable-Constraint Interactions: A
Survey. Algorithms” by Ganian and Ordyniak published in the year 2019

STP Model 7
2. “An integer programming approach for the time-dependent traveling salesman problem
with time windows. Computers & Operations” by Montero, Méndez-Díaz, and Miranda-
Bront published in the year 2017
3. “An ILP and simulation model to optimize search and rescue helicopter
operations. Journal of the Operational Research Society” Karatas, Razi, and Gunal
published in the year 2017
4. “The traveling salesman problem and its application in logistic practice. WSEAS
Transactions on Business and Economics” by Filip and Otakar published in the year
2011
5. “Models and algorithms for the asymmetric traveling salesman problem: an experimental
comparison. EURO Journal on Transportation and Logistics” published in the year 2012
The articles explain various problems in the supply chain that the TSP and ILP model address in
the world. They also highlight some of the limitations of the TSP, among other aspects.
Challenges in the supply chain can be solved by TPS
According to Montero, Méndez-Díaz, and Miranda-Bront (2017), TPS helps to address
various problems in the supply chain. The authors believe that addressing the problems sheds a
lot of light in the transport infrastructure, urban logistics, and city planning. One of the
challenges that have become prevalent in most cities and towns of the world is congestion. The
problem is expected to get worse in the years to come; hence the need to come up with ways of
addressing such challenges that are experienced in the supply chain management is very
important in addressing both current and future problems. Montero, Méndez-Díaz, and Miranda-
Bront (2017) consider the travel time between two locations to have a fixed value along some
given time horizon when addressing the traveling salesperson problem. The authors acknowledge

STP Model 8
that the recent past years have seen development and incorporation of more sophisticated travel
time functions that have helped to work out solutions that are much closer to the expected
situations in real-world operations.
Filip and Otakar (2011) believe that TPS has a critical task in logistic transport. The
authors succinctly prove that the optimization of the circular transport task is still an instrumental
aspect of transport management logistics. Some of the benefits that the authors still believe the
supply chain can enhance as a result of advancing the optimization of circular transport
management include saving time, fuel, and cost. The three factors are highly instrumental
aspects. On the other hand, Roberti, and Toth (2012), address how the TSP problem effectively
helps to work out effective solutions for the asymmetric traveling salesperson problem. They
believe that the asymmetric traveling salesman problem is solved with the help of the ILP model,
and it is thus effective in linear programming. Karatas, Razi, and Guna (2017) believe that the
use of ILP and also the consideration of the TSP can help to enhance maritime search and rescue
operations. They believe that the Maritime and rescue operations are more or less the same as the
multiple traveling salesman problems and thus can be modeled with the help of the ILP model to
find viable solutions in offering help to the victims who need help at sea. They believe that
enhancing the operations of the Maritime search and rescue operations helps to reduce the
number of casualties significantly.
Similarities and differences of the literature
The five articles that are being considered have a number of similarities and differences
that exist between them. The first significant and notable similarity that exists between the
articles is the fact that they both appreciate TSP and believe that it has added value to various
areas of application. The applications of the TSP in various areas of application in the article are

STP Model 9
supported by various models, although in the five articles, the ILP model is highly focused.
Ganian and Ordyniak (2019), consider the exploitation of the interaction of the variable
constraints in ILP as a way of enhancing the application of the variable constraints as a way of
enhancing the solutions of the TSP. Karatas, Razi, and Gunal (2017) explain how the ILP model
can be used to enhance the success of Maritime search and rescue operations, which is a form of
multiple TSP.
Though not very intensively, Montero, Méndez-Díaz, and Miranda-Bront (2017) briefly
mention how the ILP model can be effective in the application of the time-dependent TSP. The
authors do not go into much detail regarding the model because they consider the dynamic
programming techniques and the standard commercial solvers. Roberti and Toth (2012) focus on
the ILP model in showing how the model and algorithm, while Filip and Otakar (2011), like the
other authors, also apply the ILP model to enhance the application of TSP in logistic practices.
The last significant similarity is the fact that all the articles are current because their range of
year of publication is between the year 2011 and 2019. The information that they all carry is
current and more accurate.
The main difference between the articles is that they consider the TSP in different areas
of application ranging from search and rescue operations to vehicle routing, process scheduling,
and network hub location, among others. The other difference in the articles is that not all of
them focus more on the ILP model extensively. For instance, the Montero’s article does not
focus on ILP in-depth although while the Karatas’ article focuses more on the ILP as it considers
addressing TSP.

STP Model 10
Limitations of TSP
There are a few limitations that are experienced when considering the TSP model. For
instance, Filip, and Otakar (2011), argue that there are limitations in the TSP model within the
logistic practice that may be considered either within the model or outside the model in other
instances. One of the limitations that they consider when looking at the model is capacity
limitations that might be experienced in some situations (Filip, and Otakar 2011).
Step 3: Summary and findings
In conclusion, the traveling Salesperson Problem is an important typical problem in linear
programming because the understanding of its solution has a wide range of applications
(Altmanová, Knop and Koutecký 2019). The Integer Linear Programming model is a perfect
mathematical model that clearly illustrates the application of the TSP (Greco 2008). The example
above illustrates how TSP can be applied to determine the shortest distance between customers
in different cities by a bread distributor. The literature review section clearly and explicitly the
types of problems that the model solves it compares the similarities and the differences of the
articles and gives the limitations of the TSP model. The paper is thus effective extensive and
clearly gives a perfect example of a model in the field of operations research.

STP Model 11
References
Altmanová, K., Knop, D. and Koutecký, M. (2019). Evaluating and tuning n-fold integer
programming. Journal of Experimental Algorithmics (JEA), 24(1), pp.1-22.
Brucato, C. (2013). The traveling salesman problem (Doctoral dissertation, University of
Pittsburgh).
Carroll, P. and Keenan, P. (2019). Decision Making Using Exact Optimization Methods in
Sustainable Transportation. In Sustainable Transportation and Smart Logistics (pp. 263-283).
Elsevier.
Filip, E. and Otakar, M. (2011). The travelling salesman problem and its application in logistic
practice. WSEAS Transactions on Business and Economics, 8(4), pp.163-173.
Ganian, R. and Ordyniak, S. (2019). Solving Integer Linear Programs by Exploiting Variable-
Constraint Interactions: A Survey. Algorithms, 12(12), p.248.
Greco, F. ed., (2008). Traveling salesman problem. BoD–Books on Demand.
Karatas, M., Razi, N. and Gunal, M.M. (2017). An ILP and simulation model to optimize search
and rescue helicopter operations. Journal of the Operational Research Society, 68(11), pp.1335-
1351.
Margot, F. (2010). Symmetry in integer linear programming. In 50 Years of Integer
Programming 1958-2008 (pp. 647-686). Springer, Berlin, Heidelberg.

STP Model 12
Matai, R., Singh, S.P. and Mittal, M.L. (2010). Traveling salesman problem: an overview of
applications, formulations, and solution approaches. Traveling salesman problem, theory and
applications, 1.
Mo, H. and Xu, L. (2010), June. Biogeography migration algorithm for traveling salesman
problem. In International Conference in Swarm Intelligence (pp. 405-414). Springer, Berlin,
Heidelberg.
Montero, A., Méndez-Díaz, I. and Miranda-Bront, J.J. (2017). An integer programming approach
for the time-dependent traveling salesman problem with time windows. Computers & Operations
Research, 88, pp.280-289.
Pferschy, U. and Staněk, R. (2017). Generating subtour elimination constraints for the TSP from
pure integer solutions. Central European journal of operations research, 25(1), pp.231-260.
Rasmussen, R. (2011). TSP in Spreadsheets–a Guided Tour. International Review of Economics
Education, 10(1), pp.94-116.
Roberti, R., & Toth, P. (2012). Models and algorithms for the asymmetric traveling salesman
problem: an experimental comparison. EURO Journal on Transportation and Logistics, 1(1-2),
113-133.
Salvador, T., 2010. The traveling salesman problem: a statistical approach. Report within the
scope of the program “Novos Talentos em Matemática”—Fundação Calouste Gulbenkian,
Portugal.
Stanek, R., Greistorfer, P., Ladner, K. and Pferschy, U. (2018). Geometric and LP-based
heuristics for the quadratic travelling salesman problem. arXiv preprint arXiv:1803.03681.