Trigonometry Assignment: Solving Engineering Measurement Problems

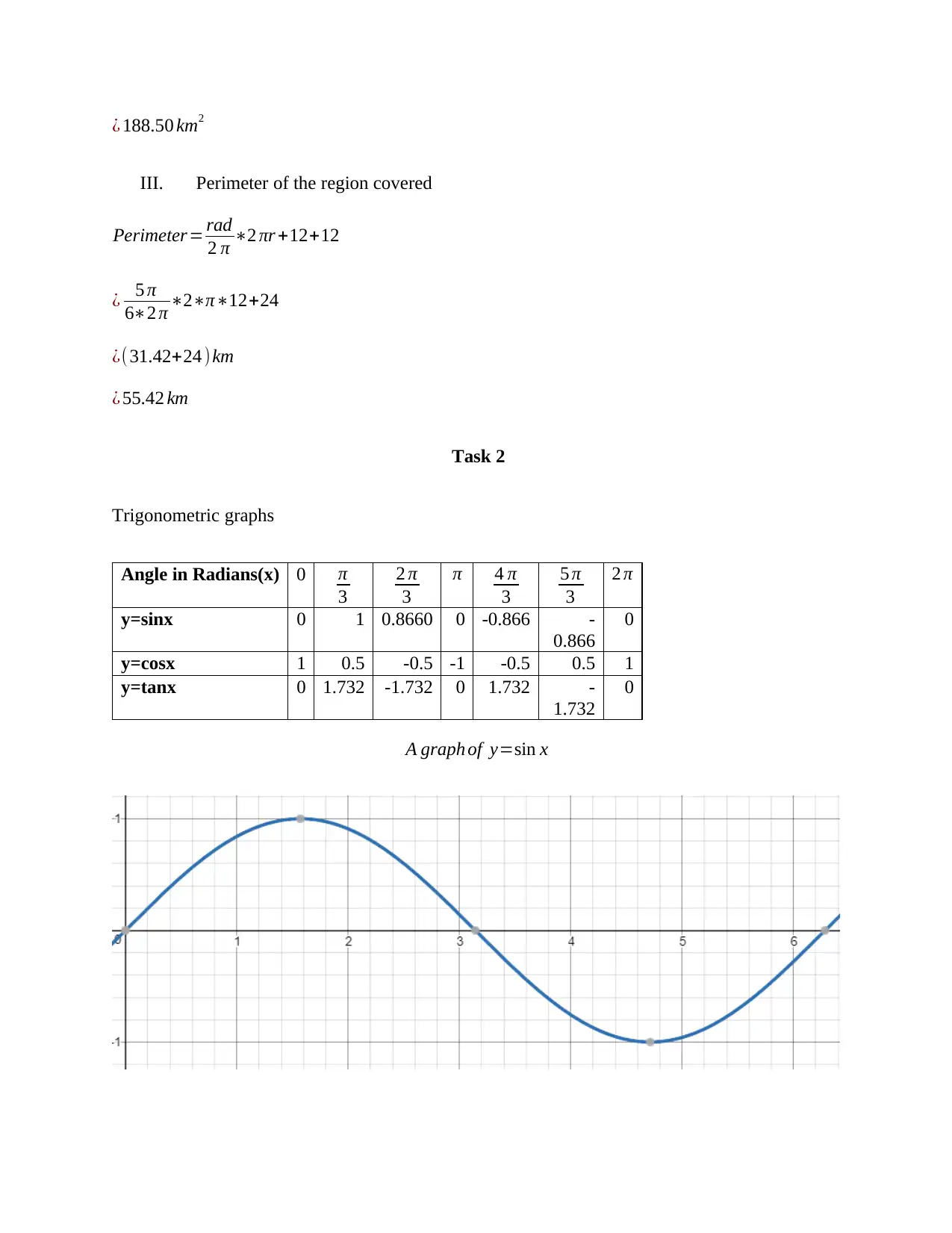
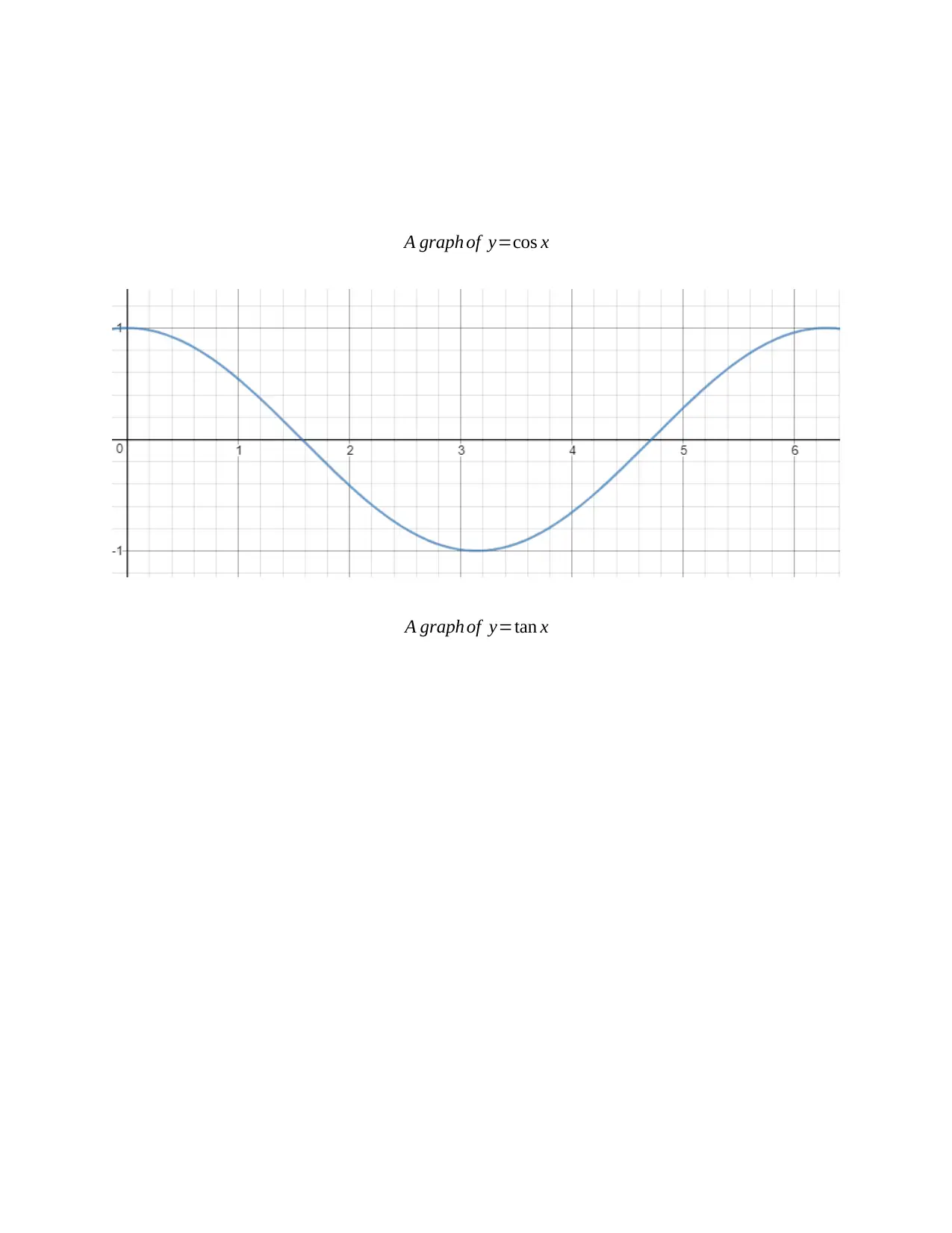
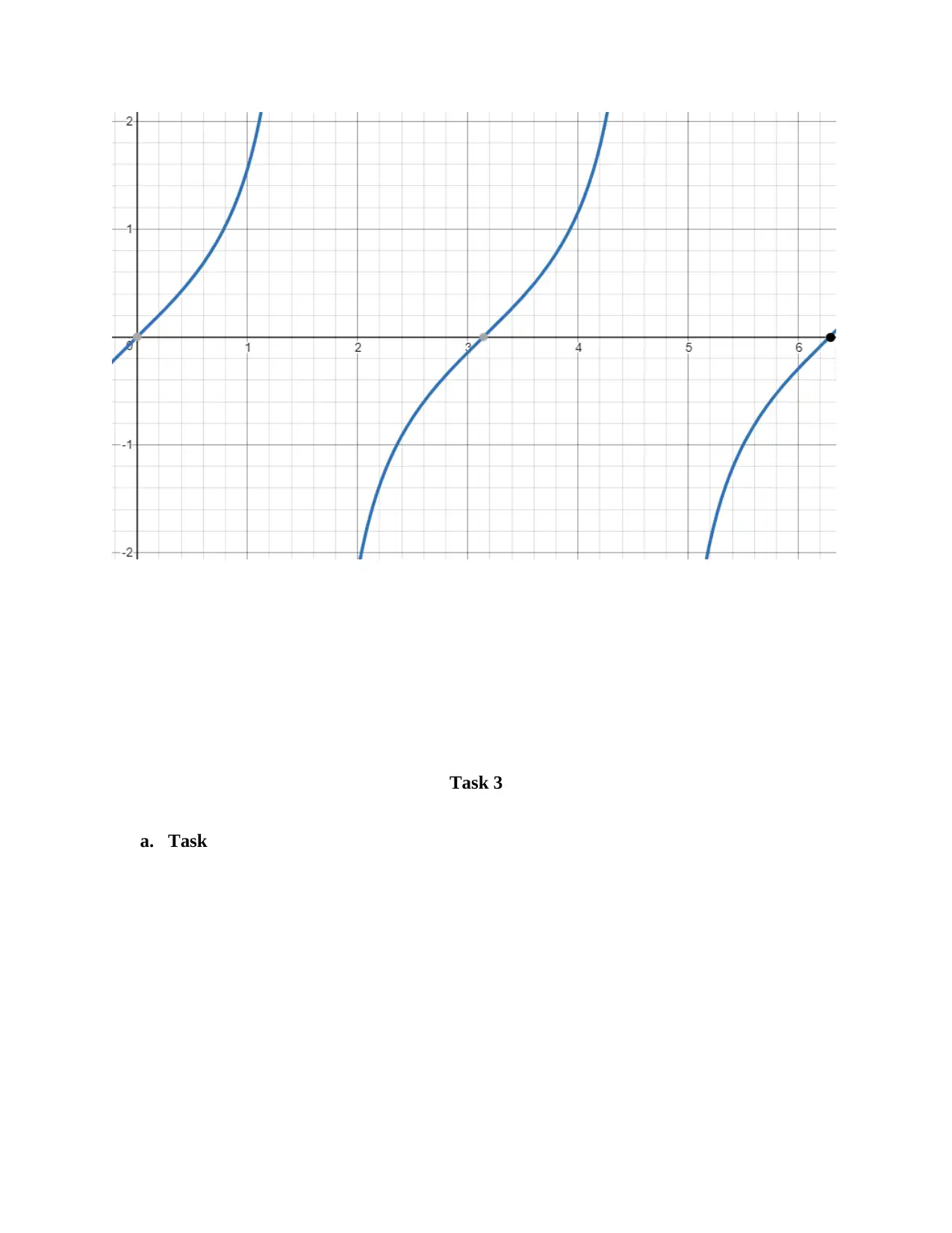
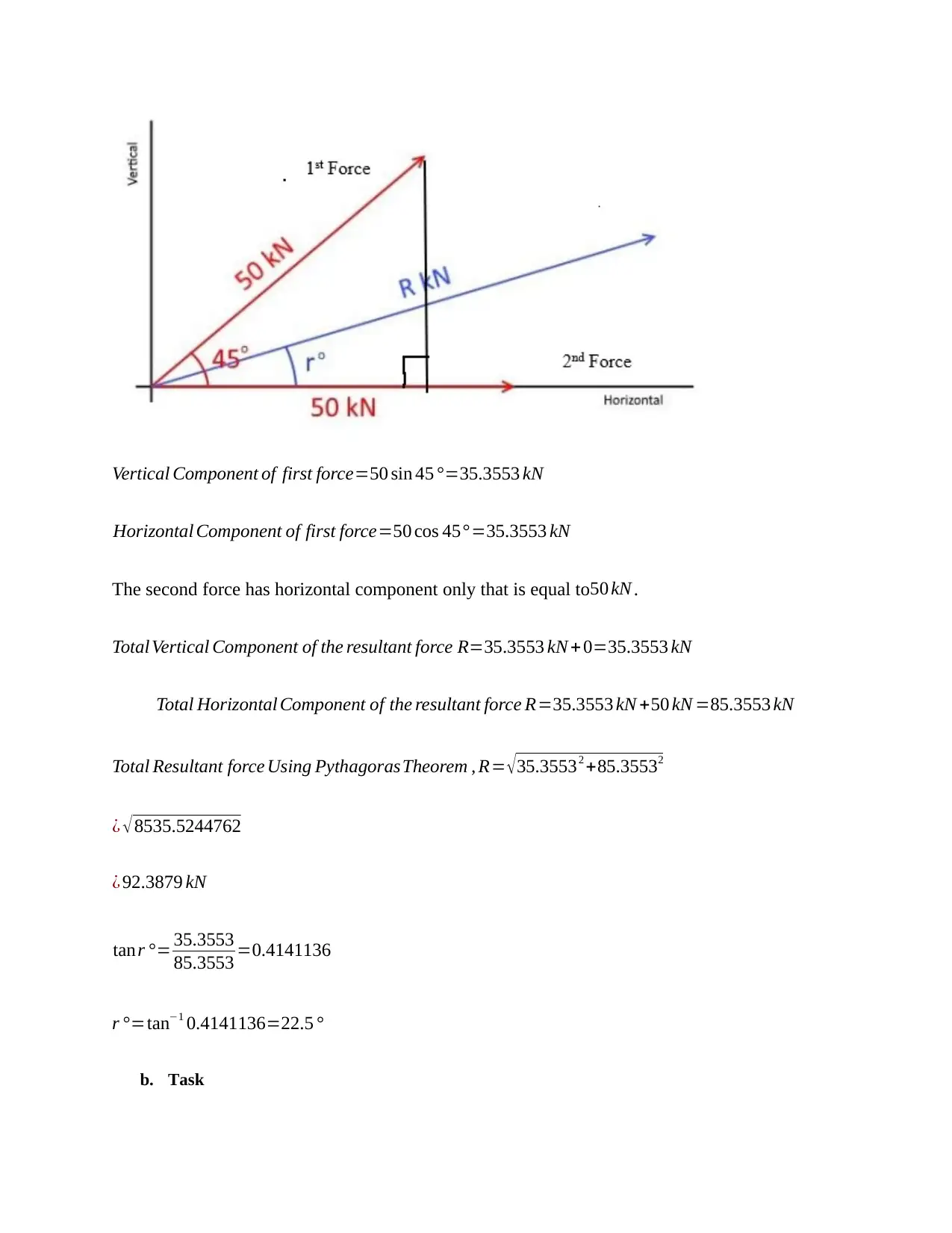
This assignment solution covers a range of trigonometry concepts relevant to engineering applications. Task 1 addresses circular and triangular measurement problems using sine, cosine, and tangent functions, including calculations of ladder lengths and angles, and conversions between degrees and radians. Task 2 involves sketching trigonometric functions (sin, cos, tan) over a complete cycle. Task 3 presents practical engineering problems solved using the sine and cosine rules to determine forces and lengths. Finally, Task 4 focuses on calculating surface areas and volumes of various regular solids such as open cylinders, triangular prisms, and spheres. The solution demonstrates a comprehensive understanding of trigonometric principles and their application in engineering contexts.

Trigonometry Assignment
Student’s Name
Institution Affiliation

Task 1
Part a
I. How far up does the ladder reach
Using the sine rule , 1.4
Sinθ = 5
sin 90
Sinθ=1.4 sin 90
5 =0.28
θ=sin−1 0.28=16.26 °
Wall length=5 cos 16.26 °=4.80 m
We obtain the same answer using Pythagoras theorem as follows.
x= √52−1.42=4.8 m
II. Minimum length of the ladder. Given that the value of height =4.5 and the
θ=90 °−74 °=16°
cos ( 16 ° ) = 4.5
Ladder Length

Ladder Length= 4.5
cos ( 16 ° ) =4.68 m
III. The angle at which the ladder meets the horizontal ground, given that the ration for
ladder horizontal to vertical is 1:4
Tanθ= Opposite
Adjacent = 4
1 =4
θ=tan−1 (4)=75.96° ≅ 76.0 °
Part b
I. 150 ° to radian
180 °=π radian,
Therefore, 150 °will be given by
150°
180° π =5
6 π radian
II. Area of the region covered
Area=rad
2 π ∗π r2
¿ 5 π
6∗2 π ∗π∗122

¿ 188.50 km2
III. Perimeter of the region covered
Perimeter= rad
2 π ∗2 πr +12+12
¿ 5 π
6∗2 π ∗2∗π∗12+24
¿( 31.42+24 ) km
¿ 55.42 km
Task 2
Trigonometric graphs
Angle in Radians(x) 0 π
3
2 π
3
π 4 π
3
5 π
3
2 π
y=sinx 0 1 0.8660 0 -0.866 -
0.866
0
y=cosx 1 0.5 -0.5 -1 -0.5 0.5 1
y=tanx 0 1.732 -1.732 0 1.732 -
1.732
0
A graph of y=sin x

A graph of y=cos x
A graph of y=tan x

Task 3
a. Task

Vertical Component of first force=50 sin 45 °=35.3553 kN
Horizontal Component of first force=50 cos 45°=35.3553 kN
The second force has horizontal component only that is equal to 50 kN .
Total Vertical Component of the resultant force R=35.3553 kN + 0=35.3553 kN
Total Horizontal Component of the resultant force R=35.3553 kN +50 kN =85.3553 kN
Total Resultant force Using PythagorasTheorem , R= √ 35.35532 +85.35532
¿ √ 8535.5244762
¿ 92.3879 kN
tanr °= 35.3553
85.3553 =0.4141136
r °=tan−1 0.4141136=22.5 °
b. Task

Cosine rule: c2=a2+b2−2 abcosC
In the above case, the length of the tie will be given by
( length ) 2=5.12 ×62 −2× 5.1× 6 ×cos 28=7.9736
length= √7.9736=2.8238 m
The value of θ, will be given by
6
sinα = 2.8238
sin 28
sinα= 6 sin 28
2.8238 =0. 99753
α =sin−1 0. 99753=85.97 °
The θ will be given by
θ=180° −85.97 °=94.03 °
Task 4
I. Open cylinder:
Volume of the open cylinder

V =π r2 l
¿ π∗422∗150
¿ 831 , 265.416 mm3
Surface area of an open cylinder:
S . A=π r2 +2∗2 πrl
¿ π∗422+2∗π∗42∗150
¿ 5 , 541.77+39 ,584.06=45 ,125.84 mm2
II. Triangular prism
Volume of a triangular prism is given by:
V = 1
2 ( bh )∗L
¿ 1
2 ( 16∗72 )∗38
¿ 21 , 888 mm3
Surface area of the triangular prism
S . A=bh+lb+2 ls
s= √722 +82 =72.443 mm
S . A=16 ×72+38 ×16 +2× 38 ×72.443=¿ 7265.668 mm2
III. Sphere

Volume of sphere is given by:
V = 4
3 π r3= 4
3 ∗π∗253=65 , 449.85 mm3
Surface area of sphere is given by:
S . A=4 π r 2=4∗π∗252=7 , 853.98 mm2