Trigonometry Assignment: Foundations of Mathematics, Unit 1

This document presents a comprehensive solution to a trigonometry assignment, likely for a Foundations of Mathematics course. It covers two main parts: right-angled and non-right angled trigonometry, and triangulation. The first part delves into the sine and cosine rules, including their applications in solving for unknown sides and angles of triangles, with detailed examples and calculations. The second part focuses on triangulation, using the cosine rule to determine distances and positions based on angle measurements from different points, with a specific case involving mobile towers and the location of a person. The solution provides step-by-step workings and explanations for each problem, including diagrams, calculations, and interpretations of results, offering a complete guide to understanding and solving trigonometry problems.

Running Head: Trigonometry Assignment 1
Trigonometry Assignment
Name
Institution Affiliation

TRIGONOMETRY ASSIGNMENT 2
Part A: Right-Angled and Non-Right Angled Trigonometry
Question 1: Sine rule
Part a)
The sine rule states that the ratio of the side of a triangle and the sine of the opposite angle to that
side is constant for all the three sides and the respective angles.
Considering the triangle ABC below, the sine rule is stated as
a
sin A = b
sin B = c
sin C
Where a , b , care the lengths of the sides and A , B , Care the angles opposite to each side
respectively (Flanders, 2014).
Part b)
The sine rule can be used when the length of one side of the triangle and its opposite angle is
known. If the length of one of the remaining sides or the magnitude of one of the remaining
angles is known, then all the angles and the sides of the triangle can be solved using the sine rule.
The rule cannot be used when all the sides are missing or all the angles are missing (Stewart &
Tall, 2015).
Part c)
Suppose a=6 cm ,∠ A=50 °and∠ C=72°find the remaining sides of the triangle.
a
sin A = b
sin B = c
sin C
c= a × sinC
sin A = 6 ×sin 72
sin 50 =7.45 cm ( 2 d . p ) .
The angles in a triangle add up to 180 °
BA
C

TRIGONOMETRY ASSIGNMENT 3
∠ B=180 °− ( 72+50 ) =58 °
b= a ×sin B
sin A =6 × sin 58
sin50 =6.64 cm
Part d)
Supposea=4 cm, b=6 cmand∠ B=54 ° ,find the remaining angles of the triangle.
a
sin A = b
sin B = c
sin C
sin A= a× sin B
b = 4 ×sin 54
6 =0.539
∠ A=sin−1 0.539=33.62 °
The angles in a triangle add up to 180 °
∠ C=180 °− ( 54+33.62 ) =92.38 °
Question 2: The cosine rule
Part a)
The cosine rule states that if sides aand bare known and ∠ Cis the angle between the sides
(included angle), then side ccan be obtained by the following formula (Flanders, 2014)
c2=a2+ b2−2 ab cos C
Also, given aand c and∠C, the sidec can be obtained by
b2=a2 +c2−2 ac cos B
Also, given band c and∠ A, the sidea can be obtained by
a2=b2 +c2−2 bc cos A
BA
C

TRIGONOMETRY ASSIGNMENT 4
Part b)
The cosine rule can be used when two sides and the include angle are known in a triangle. It is
also useful when all the sides of the triangle are known and all the angles are unknown.
The cosine rule cannot be used when only one or no side is known. Moreover, when two sides
are known and the given angle is not an included angle, then the cosine rule cannot be applied
(Stewart & Tall, 2015).
Part c)
Suppose a=5 cm ,b=6 cmand∠C=72°find the remaining side c of the triangle.
c2=a2+ b2−2 ab cos C
c2=52+62−2 ×5 ×6 cos 72
c2=42.459
c=6.52cm
Part d)
Suppose a=5 cm ,b=6 cmandc=7 cmfind all the angles of the triangle.
c2=a2+ b2−2 ab cos C
Rearranging∠ C=cos−1
( a2 +b2−c2
2 ab )=cos−1
( 52+ 62−72
2 ×5 ×6 )=78.46 °
b2=a2 +c2−2 ac cos B
Rearranging∠ B=cos−1
( a2 +c2−b2
2 ac )=cos−1
( 52 +72−62
2× 5× 7 )=57.12 °
a2=b2 +c2−2 bc cos A
Rearranging∠ A=cos−1
( b2+ c2−a2
2 bc )=cos−1
( 62+72−52
2× 6 ×7 )=44.42 °

TRIGONOMETRY ASSIGNMENT 5
Question 3
Part a)
∠ BAC=60 °
∠ DBE=10 °
Since ∠ DBA=90 ° , ∠ ABE=90° −10 °=80 °
Consider triangle ABC,
BC= AB sin 60°=800 sin 60 °=692.82 m
Eagle Nest Elevation=2000+692.82=2692.82m
Consider the triangle ABE from the figure.
Using cosine rule, we can calculate the length AE
AE2= AB2+ EB2 −2 ( AB ) ( EB ) cos (∠ ABE )
AE2=8002 +3002−2 ( 800 ) ( 300 ) cos 80 °
A
B
E
A
B
C

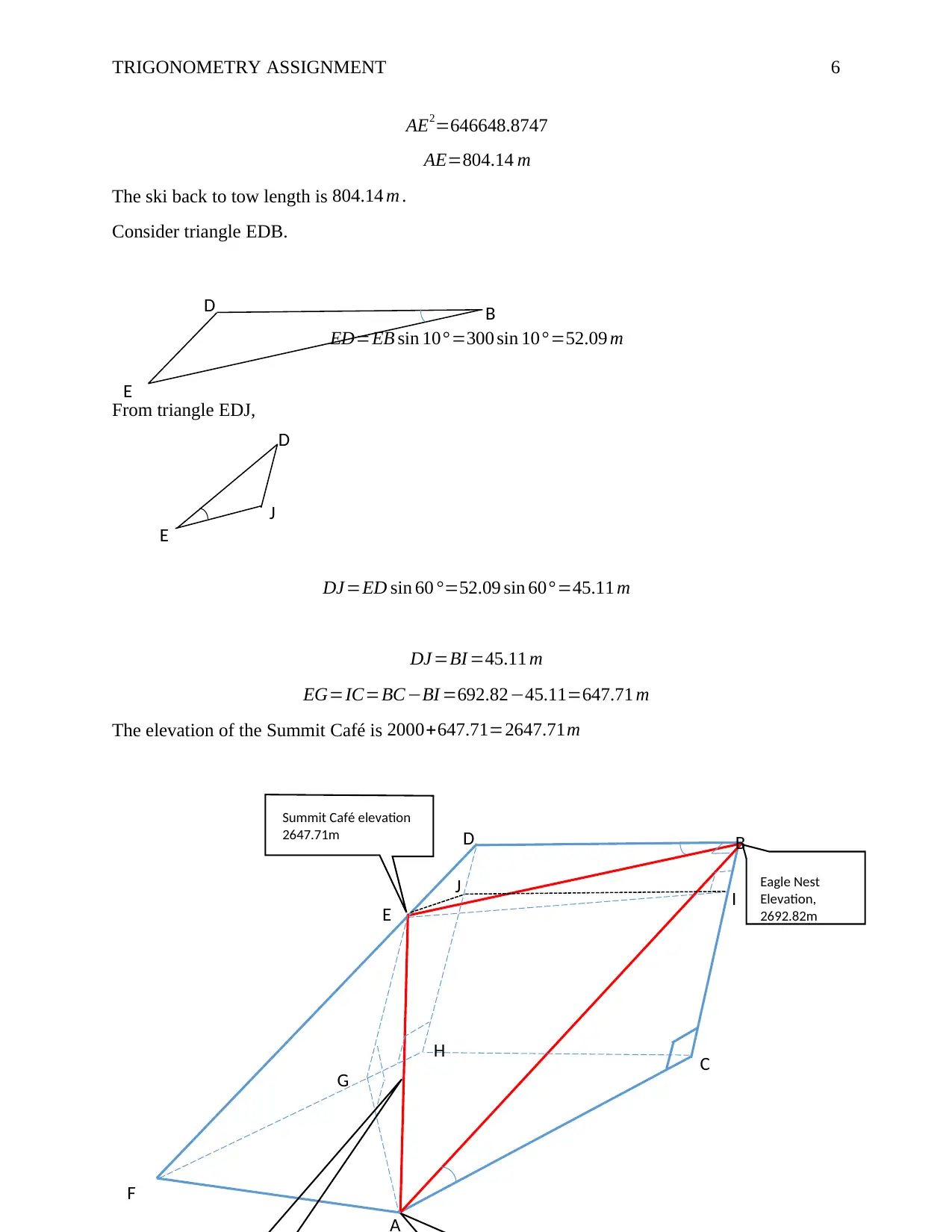
TRIGONOMETRY ASSIGNMENT 6
AE2=646648.8747
AE=804.14 m
The ski back to tow length is 804.14 m .
Consider triangle EDB.
ED=EB sin 10° =300 sin 10°=52.09 m
From triangle EDJ,
DJ=ED sin 60 °=52.09 sin 60° =45.11 m
DJ=BI =45.11 m
EG=IC=BC −BI =692.82−45.11=647.71 m
The elevation of the Summit Café is 2000+647.71=2647.71m
BD
E
A
B
C
D
E
F
G
H
I Eagle Nest
Elevation,
2692.82m
Summit Café elevation
2647.71m
J
D
E
J

TRIGONOMETRY ASSIGNMENT 7
Part b)
Considering triangle EBI, angle ∠ BEIis the angle that the first ski leg makes with the horizontal
plane and can be calculated in the following fashion (Stewart & Tall, 2015).
EI =EB cos ∠ BEI , BI =EBsin ∠ BEI
BI=45.11 m, EB=300 m
∠ BEI=sin−1
( 45.11
300 )=8.65°
ans : 8.65°
Part c)
Considering triangle AGE, ∠ GAEis the angle the second ski leg makes with the horizontal plane
AE=804.14 m, EG=647.71 m
EG= AE sin∠ GAE
∠ GAE=sin−1
( 647.71
804.14 )=53.66 °
ans : 53.66 °
Ski back to tow length
804.14m
Erehwon ski tow
elevation 2000m
B
E I
A
E
G

TRIGONOMETRY ASSIGNMENT 8

TRIGONOMETRY ASSIGNMENT 9
PART B: Triangulation
Question 1
Part a)
Considering the two mobile towers to be at point A (western tower) and B (eastern tower) as in
the figure below, there are two possible location of a person from the given information, at point
C and D. Point C is south of the fire trail while point D is north of the fire trail. The figure below
is an illustration (Flanders, 2014).
Using cosine rule, the angle ∠ DAB=∠ CABcan be determined. Similarly, angle∠ DBA=∠CBA
can be calculated to further pinpoint the person’s location.
Part b)
Applying the cosine rule,
DB2= AB2+ AD2−2 ( AB ) ( AD ) cos (∠ DAB )
∠ DAB=cos−1
( AB2 + AD2−DB2
2 ( AB ) ( AD ) )=cos−1
( 60002 +52002 −24152
2 ( 6000 ) ( 5200 ) )=23.54 °
∠ DAB=∠CAB=23.54 °
Similarly,
AD2=AB2 + D B2−2 ( AB ) ( D B ) cos ( ∠ DBA )
∠ DBA=cos−1
( AB2 + D B2− AD2
2 ( AB ) ( DB ) )=cos−1
( 60002+ 24152−52002
2 ( 6000 ) ( 2415 ) )=59.31 °
∠ DBA=∠CBA=59.31 °
A
5200 m
2415 m
2415 m
5200 m
6000m
B
D
C
E

TRIGONOMETRY ASSIGNMENT 10
From the western tower, ∠ DABand ∠ CABare used.
23.54 °=23° 32' 24'' =23° 32'to the nearest minute.
ans :Position at point D from the western tower: N 23 °32' E
Position at point C from the western tower: S 23 ° 32' E
Part c)
Distance CE from the road to the person is half the distance CD.
CD2= AC2 + AD2−2 ( AC ) ( AD ) cos ( ∠ DAC )
CD2=52002 +52002−2 ( 5200 ) ( 5200 ) cos ( ∠ ( 23.54 ° × 2 ) )=17252789.08
CD=4153.65 m
CE=0.5× CD=0.5 × 4153.65=2076.83 mis the distance from the road to the person.
ans : 2076.83m
Question 2
Part a)
Since the motion is due north, it must have originated from point C.
CE=2076.83 m , hence EF=2076.83−100=1976.83 m
EB= √ CB2−CE2= √ 24152−2076.832=1232.48 m
A
5200 m
2415 m
2415 m
5200 m
6000m
B
D
C
E
F100 m

TRIGONOMETRY ASSIGNMENT 11
BF= √ EB2 + EF2 = √ 1232.482+1976.832 =2329.56 m
BC−BF=2415−2329.83=85.17 m
Hence the person is BC−BF=2415−2329.83=85.17 mcloser to the eastern tower.
Part b)
Walking further 100 mdue north, EG=2076.83−200=1876.83 m
BG= √ EB2+ EG2= √ 1232.482 +1876.832=2245.33 m
2329.56−2245.33=84.23 m
The person moves 84.23 mcloser to the east tower by moving a further 100m due North.
It can be observed that EBG and EBF (as illustrated in the figure above)are not congruent hence
the ratio of changes on the sides cannot be the same.
A
5200 m
2415 m
2415 m
5200 m
6000m
B
D
C
E
F100 m
G

TRIGONOMETRY ASSIGNMENT 12
References
Stewart, I., & Tall, D. (2015). The Foundations of Mathematics (3rd ed., pp. 1-235).
Oxford: Oxford University Press.
Flanders, H. (2014). Elementary Functions and Analytic Geometry (1st ed.). Boston:
Elsevier Science.