Complete Trigonometry Assignment Solution for Calculus Course

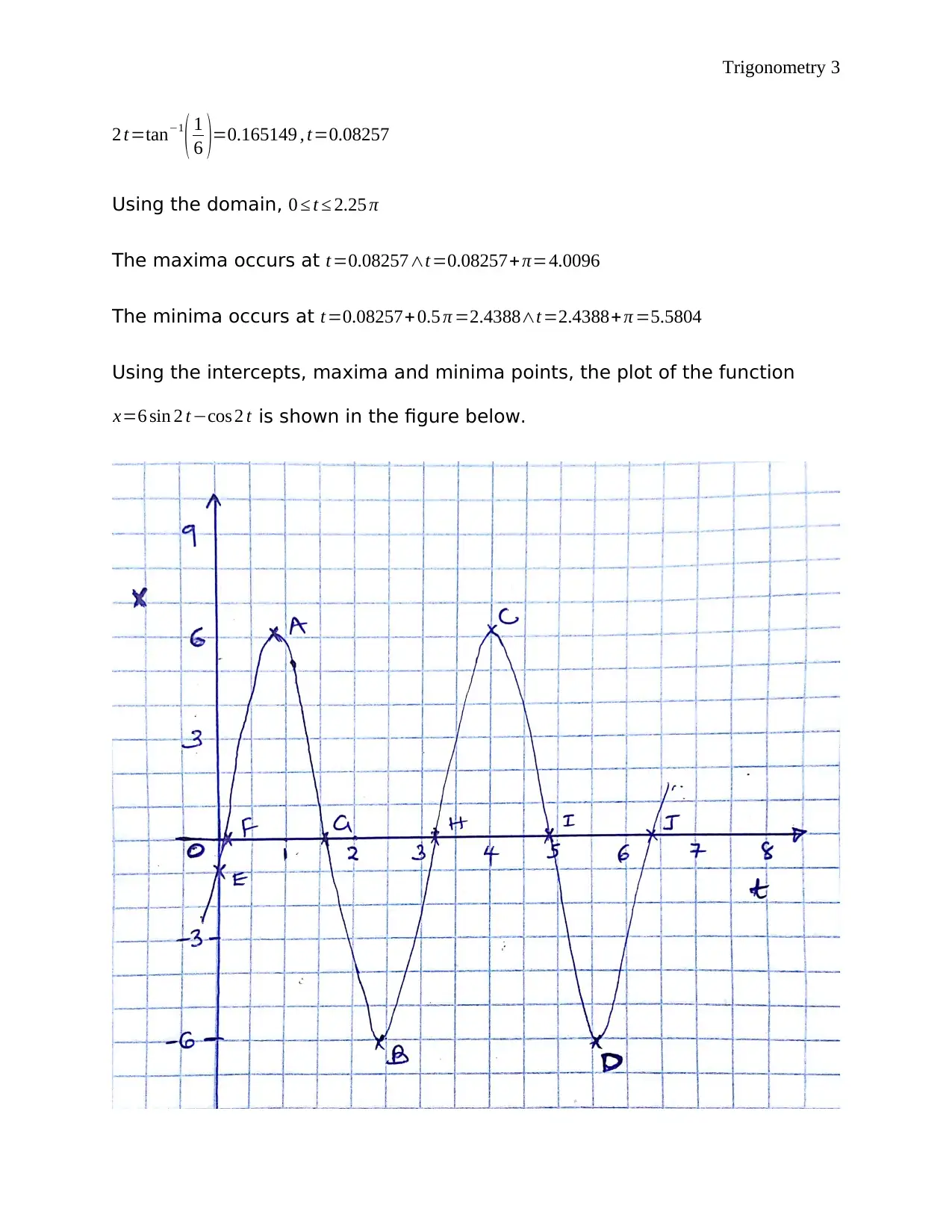
This document presents a detailed solution to a trigonometry assignment, addressing several key concepts within calculus and analysis. The solution encompasses the analysis of particle motion, determining maximum distances and sketching graphs to illustrate the motion. It also includes the modeling of temperature variations using trigonometric functions, calculating temperatures at specific times, and identifying maximum and minimum temperatures. Furthermore, the assignment delves into solving trigonometric equations, utilizing identities and applying them within a given domain. The solution provides step-by-step explanations and graphical representations to enhance understanding and facilitate learning.

Trigonometry 1
Trigonometry
Student’s Name
Course
Professor’s Name
University
City (State)
Date

Trigonometry 2
Trigonometry
Question 1
Part i
x=6 sin 2 t−cos 2 t
Maximum distance of particle occurs when, d x
dt =0
d x
dt = d
dt ( 6 sin 2t−cos 2t )=12 cos 2 t +2 sin 2 t=0
12 cos 2 t=−2sin 2 t
sin 2t
cos 2 t =tan 2t=−6
2 t=tan−1 (−6)=1.7359
time , t=0.867971 seconds
when t=0.867971 , distance x=6 sin 1.7359−cos 1.7359=6.083 m
Part ii
The y-intercept occurs when, t=0 so that,
x=6 sin 0−cos 0=−1
x-intercepts occur when x=0 so that,
6 sin 2 t=cos 2 t
sin 2t
cos 2 t =tan 2t= 1
6

Trigonometry 3
2 t=tan−1
( 1
6 )=0.165149 , t=0.08257
Using the domain, 0 ≤ t ≤ 2.25 π
The maxima occurs at t=0.08257∧t=0.08257+ π=4.0096
The minima occurs at t=0.08257+ 0.5 π =2.4388∧t =2.4388+ π =5.5804
Using the intercepts, maxima and minima points, the plot of the function
x=6 sin 2 t−cos 2 t is shown in the figure below.

Trigonometry 4
Question 2
F ( t ) =60+10 sin π
12 (t−8) for 0 ≤ t ≤ 24
Part a
At 8:00am,
F ( 8 ) =60+10 sin π
12 ( 8−8 ) =60+10 sin 0=6 0 ℉
At 12:00pm,
F ( 12 )=60+10 sin π
12 ( 12−8 )=60+ 10sin ( π
3 )=6 8.66 ℉
Part b
F ( t )=60=60+10 sin π
12 (t−8)
10 sin π
12 (t−8)=60−60=0
sin π
12 (t−8)=0
π
12 ( t−8 ) =sin−1 0=0 , π , 2 π …
π
12 ( t−8 ) =0 ,t−8=0 , t=8 (8 :00 am)
π
12 ( t−8 ) =π , t−8=π × 12
π =12 , t=8+12=20(8 :00 pm )

Trigonometry 5
π
12 ( t−8 ) =2 π , t−8=2 π × 12
π =24 ,t =8+24=32(ignored)
Therefore, the temperature is 6 0 ℉ at 8am and 8pm.
Part c
Maximum temperature occurs when sin π
12 (t−8)=1
So that maximum temperature¿ 60+10 ( 1 )=70 ℉
So that, π
12 ( t−8 ) =sin−1 1= π
2
π
12 ( t−8 ) = π
2
t−8= π
2 × 12
π =6
t=8+ 6=14 (2 :00 pm)
Minimum temperature occurs when sin π
12 (t−8)=−1
So that minimum temperature¿ 60+10 (−1 )=50 ℉
So that, π
12 ( t−8 ) =sin−1 (−1)= 3 π
2
π
12 ( t−8 ) =3 π
2
t−8=3 π
2 × 12
π =18
t=8+18=26(2:00 am )

Trigonometry 6
Part d
t 0 2 8 10 14 20 24
x 51.34 50 60 65 70 60 51.34
Question 3
Part a
Tension=mgcosθ
If θ is very small, sinθ ≅ θ= x
L and cosθ=1−θ2
2
Tension=mgcosθ=mg (1−θ2
2 )=mg (1− ( x
L )2
2 )=mg (1−
x2
L2
2 )=mg (1− x2
2 L2 )

Trigonometry 7
Therefore, tension in the string will be mg (1− x2
2 L2 )
Part b
Restoring force ¿ mgsin θ
But, when θ is very small, sinθ≅ θ= x
L
Restoring force¿ mgsin θ=mg x
L
Part c
F=−mgsinθ where F is the restoring force.
From Newton’s second Law of Motion, F=ma so that,
F=ma=−mgsinθ=−mg x
l
ma=−mg x
l
a=−g
l x
Evidently, acceleration is directly proportional to the displacement x and in
the opposite direction.

Trigonometry 8