Trigonometry Assignment - Module 2: Inverse Trig and Triangles

This trigonometry assignment solution covers inverse trigonometric functions, their domains and ranges, and applications to solving trigonometric equations and problems related to triangles. The solution details the functions sine, cosine, and tangent, along with their inverses, and explains the importance of restricted domains. It provides step-by-step solutions to problems involving inverse functions, solving trigonometric equations, and applying the Law of Sines and Law of Cosines to real-world scenarios, such as navigation. The assignment also includes examples of how to calculate distances and bearings using trigonometric principles. The solution demonstrates a strong understanding of trigonometry concepts and their practical applications.

Running Head; TRIGONOMETRY
TRIGONOMETRY
Name
Institute of Affiliation
Date

TRIGONOMETRY 2
I. Inverse Functions
1.
a. State the functions, sine, cosine and tangent. Then state the domain and range of these
functions.
Function Domain Range
Sin −∞ ≤ x ≤ ∞ ∞
Cosine −∞ ≤ x ≤ ∞ ∞
Tangent −∞ ≤ x ≤ ∞ ∞
a) Why is it so important to restrict these function’s domains to be one-to-one?
The function can find values of large numbers up to infinity, it is important to describe
how far should a person go. For instance, since some of angles are θ+2 nπ, one has to
define the maximum value of n.
c) List the inverse of three functions sine, cosine and tangent using the appropriate notation.
Function inverse Domain Range
Sin Sin-1 −1 ≤ x ≤1 2
Cosine Cosine-1 −1 ≤ x ≤1 2
Tangent Tan-1 −∞ ≤ x ≤ ∞ ∞
Then name the restricted domain and range for each of these functions.
Beside each restriction sketch a drawing of the new function.

TRIGONOMETRY 3
d) Find the inverse of (𝑥) = (1/2)Cos(x). State the domain and range of both f(x) and f^-1(x)(aka
inverse).
f (x)=1
2 cos( x ).
2 f ( x )= cos x
= cos-1 x
Domain is −1 ≤ x ≤1 , this because the cosine of the angle can only be between -1 and 1.
and the range is given as shown
¿ 1−−1
= 2
2. Complete the following problems. (5 pts.)
a) Co s−1 1
2 = 60 (from the above triangle)
b) Si n−1−1
2
it is easier to find Si n−1 1
2 and then check in the quadrant where the sin has negative values
Si n−1−1
2 = 180+ Si n−1 1
2
= 180 + 30

TRIGONOMETRY 4
= 210
b) Tan−1− √ 3= ( the value has to be in the 2nd or 4th quadrant)
= 180 - Ta n−1 √3 ( for the value in the 2nd quadrant)
= 180 – 60
= 120
And /or
= 360 - Ta n−1 √ 3 ( for the value in the 4th quadrant)
= 360 – 60
= 300
c) cos (ta n−1 (8
3 ))
Starting with the value in the bracket first
ta n−1
( 8
3 ) = nπ +θ ( this is the general solution where n=0,1,2,3,4,5…)
= 69.44, 249.44, 429.44……….
Rewriting the question again
cos (69.44) = …….( taking the first value only)
= 0.351
d) sin(co s−1 ( 3
4 ))
Starting with the value in the bracket first

TRIGONOMETRY 5
co s−1 ( 3
4 )= 2 π n+θ ( this is the general solution where n=0,1,2,3,4,5… since for positive
value of cos, the angles are 1st and 4th quadrant )
= 41.41, 318.59……….
Rewriting the question again
sin( 41.41) = …….( taking the first value only)
= 0.6614
4. Solve the following equations. (8 pts.)
a) 3√ 2 + 6 cos (𝑥) = 0
6 cos (
𝑥) = -3√2
Cos(x) = - 0.5√2
x = cos1−0.5 √2
= 135,225
b) √2 Sin (x/2) -1 = 0
sin( x
2 ) = 1
√ 2
x
2 = sin−1 0.7071
X= 90, 270
c) 2 Si n2 ( x)−cos(x )=−1
since

TRIGONOMETRY 6
sin2 x+cos2 x=¿ 1¿
sin2 x= 1- cos2 x
2(1−cos2 x)−cos(x )=−1
2-2cos2 x−cos ( x )=−1
2cos2 x +cos (x)=3
Cos x = y
2 y2 +y -3=0
Y=1,-1.5
Since values of cos varies between -1 and 1, -1.5 is out of question so we move with 1.
Cos x = 1
X = cos−1 1
= 0,360… 2 nπ where n = 0,1,2,3,4….
d) Ta n2( x)sin( x)=3 sin(x)
Ta n2( x)= 3
X= tan−1 √ 3
= 60, 240…
II. Applications of Triangles; Right Triangles, Law of Sine and Law of Cosine
# 80

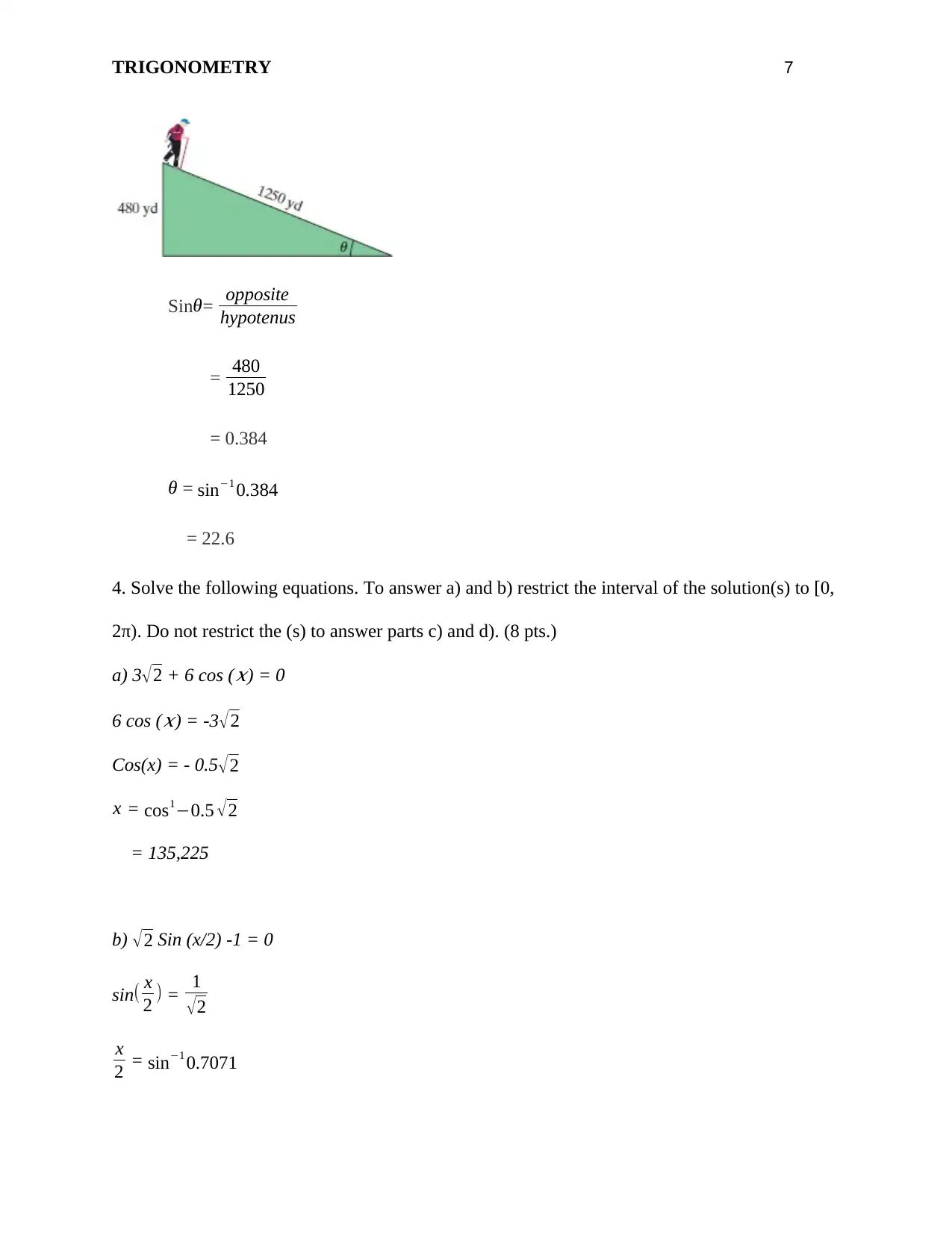
TRIGONOMETRY 7
Sinθ= opposite
hypotenus
= 480
1250
= 0.384
θ = sin−1 0.384
= 22.6
4. Solve the following equations. To answer a) and b) restrict the interval of the solution(s) to [0,
2π). Do not restrict the (s) to answer parts c) and d). (8 pts.)
a) 3√2 + 6 cos (
𝑥) = 0
6 cos (
𝑥) = -3√2
Cos(x) = - 0.5√2
x = cos1−0.5 √ 2
= 135,225
b) √2 Sin (x/2) -1 = 0
sin( x
2 ) = 1
√2
x
2 = sin−1 0.7071

TRIGONOMETRY 8
X= 90, 270
c) 2 Si n2 ( x)−cos(x )=−1
since
sin2 x+cos2 x=¿ 1¿
sin2 x= 1- cos2 x
2(1−cos2 x)−cos(x )=−1
2-2cos2 x−cos ( x )=−1
2cos2 x +cos (x)=3
Cos x = y
2 y2 +y -3=0
Y=1,-1.5
Since values of cos varies between -1 and 1, -1.5 is out of question so we move with 1.
Cos x = 1
X = cos−1 1
= 0,360… 2 nπ where n = 0,1,2,3,4….
d) Ta n2( x)sin( x)=3 sin(x)
Ta n2( x)= 3
X= tan−1 √ 3
= 60, 240…

TRIGONOMETRY 9
1. Complete either problem #56 (on page 638) or #58 (on page 639). Make sure you first
draw a picture and include it. Then complete both parts a and b showing all work. (6 pts.)
A plane leaves an airport heading S82°E at 320 mph. After 1.2 hr, it makes a 90°
counterclockwise turn to a new bearing of N8°E and travels for 45 min.
Find the plane's distance from the airport to the nearest mile.
Distance traveled 1.2 HRS= 320 mph * 1.2 hrs
= 384 miles
Distance travelled 45 min = 320 mph * 0.75 hour
= 240 miles.
Since the plane turns 9 00, the distance traveled forms two short lengths of triangle
Then
Hypotenuse= √3842 +2402
= 452.83 miles
≈ 453 miles
Find the bearing required for the plane to return to the airport. Round to the nearest degree.
ϕ = tan−1 384
240
= 57.99
≈ 580
Bearing now is given as follows;
Φ = 58 + 8
= S660W

TRIGONOMETRY 10
2. Write down the Law of Sines (seen in the rectangle on page 642). Then write the two cases
in which the Law of Sines can be used.
a
sinA = b
sinB= c
sinC
This is applied in the ship when finding the direction in the sea. This is also applied by pilots to
navigate in the air.
PDF Transcript for Lecture: Introduction to the Law of Sines
b. Create one real world example. In this example include the following
- a description of your real world example along with what needs to be determined,
(2 pts.)
- an equation, (2 pts.) and
- steps to the solution. (2 pts.)
A captain moves in the south for 3 hours at 300 mph. He then changes his course and moves
30 degrees to the east. He travels for 2 hours at the same speed. Now that he needs to travel
back, what is the shortest distance from the starting point?
3. a) Write down the Law of Cosines. Then write the two cases in which the Law of
Cosines can be used. View example 3 (page 659 – 660) on the pages. (2 pts.)
a2=b2 +c2−2 ab cosA

TRIGONOMETRY 11
EXAMPLE 3Applying the Law of Cosines
A Coast Guard ship on a routine training run leaves its base at 16 knots (nautical miles per
hour) on a course of N82°E. Three hours later, a distress call comes in from a cargo ship
located 180 nmi (nautical miles) from base at a bearing of N48°E.
a. How far is the Coast Guard ship from the cargo ship? Round to the nearest tenth of a
nautical mile.
b= 16 knots * 3
= 48 nmiles
a=√ (482+1802−2∗180∗48 cos 34)
= 142.8 nmi
b. What bearing should the Coast Guard ship follow to reach the cargo ship? Round to the
nearest tenth of a degree.
C = cos−1 ( 142. 82 + 4 82−18 02
2∗48∗142.8 )
= 135.1
θ = 135.1 – 98

TRIGONOMETRY 12
¿ N37.10E
b) Complete one of the three problems #24 (on page 662), 26 or 28 (on page 663). (4 pts.)
A boat leaves port and follows a course of N77°E at 9 knots for 3 hr and 20 min. Then, the
boat changes to a new course of S28°E at 12 knots for 5 hr.
a. How far is the boat from port?
First distance covered a = 9 nm * 3.33hrs
= 30 nmi
Second distance travelled b = 12 knots * 5
= 60 nmi
Using cosine rule
c2 = 602 +302−2∗30∗60 cos 105
C =73.7 nmi
b. Suppose that the boat becomes disabled. How long will it take a rescue boat to arrive
if the rescue