Comprehensive Trigonometry Guide: Formulas, Laws, and Identities

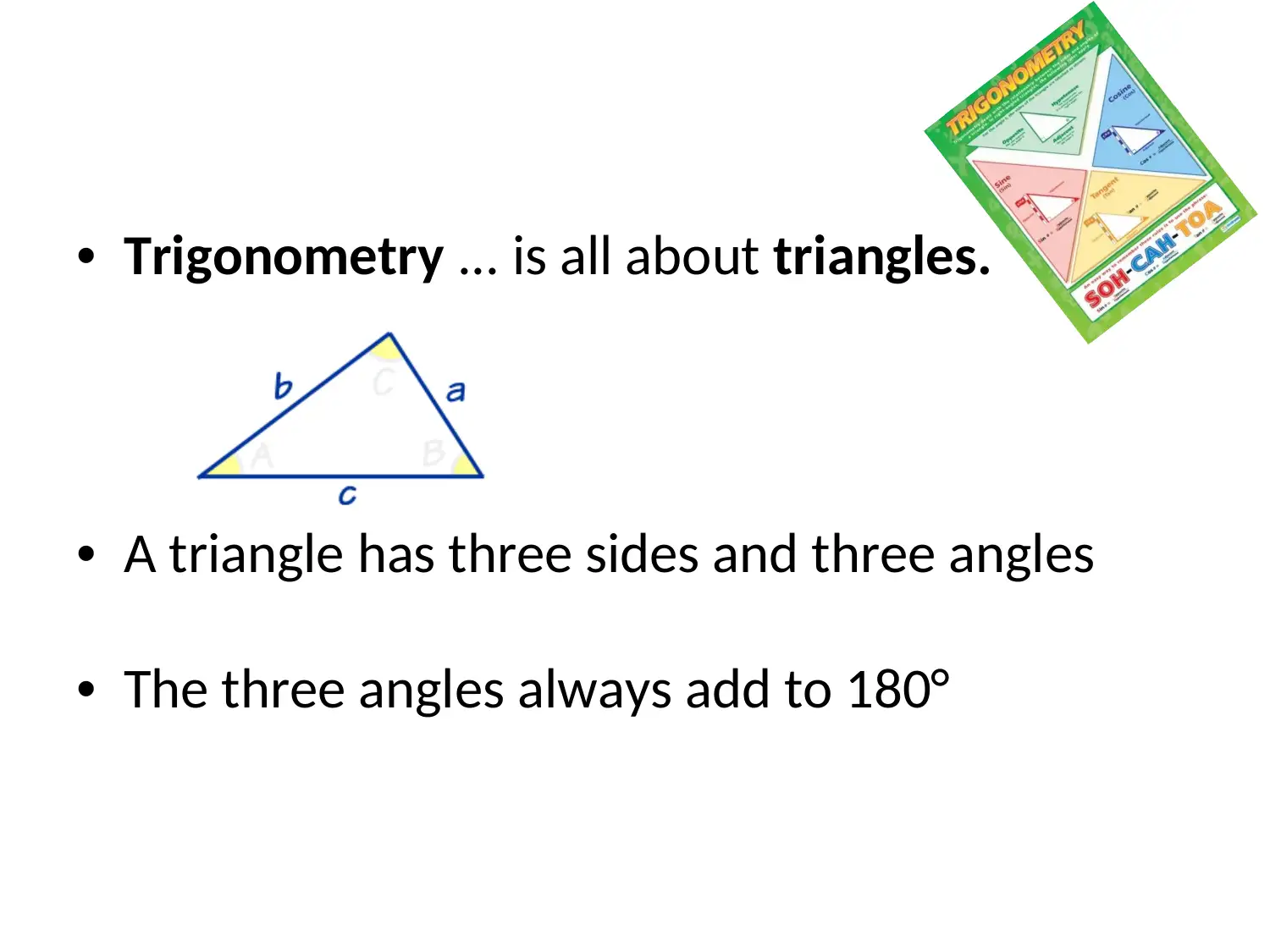
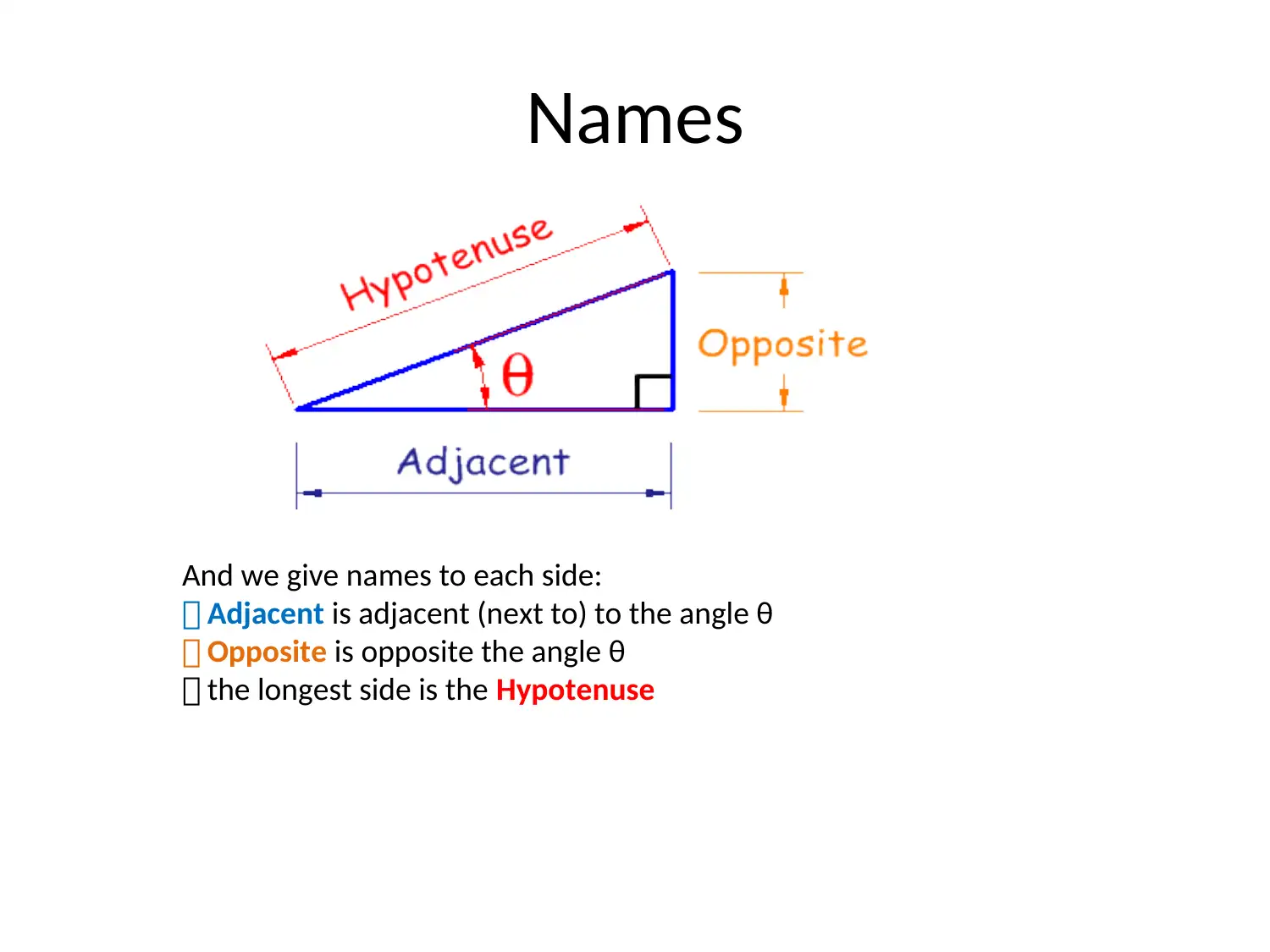
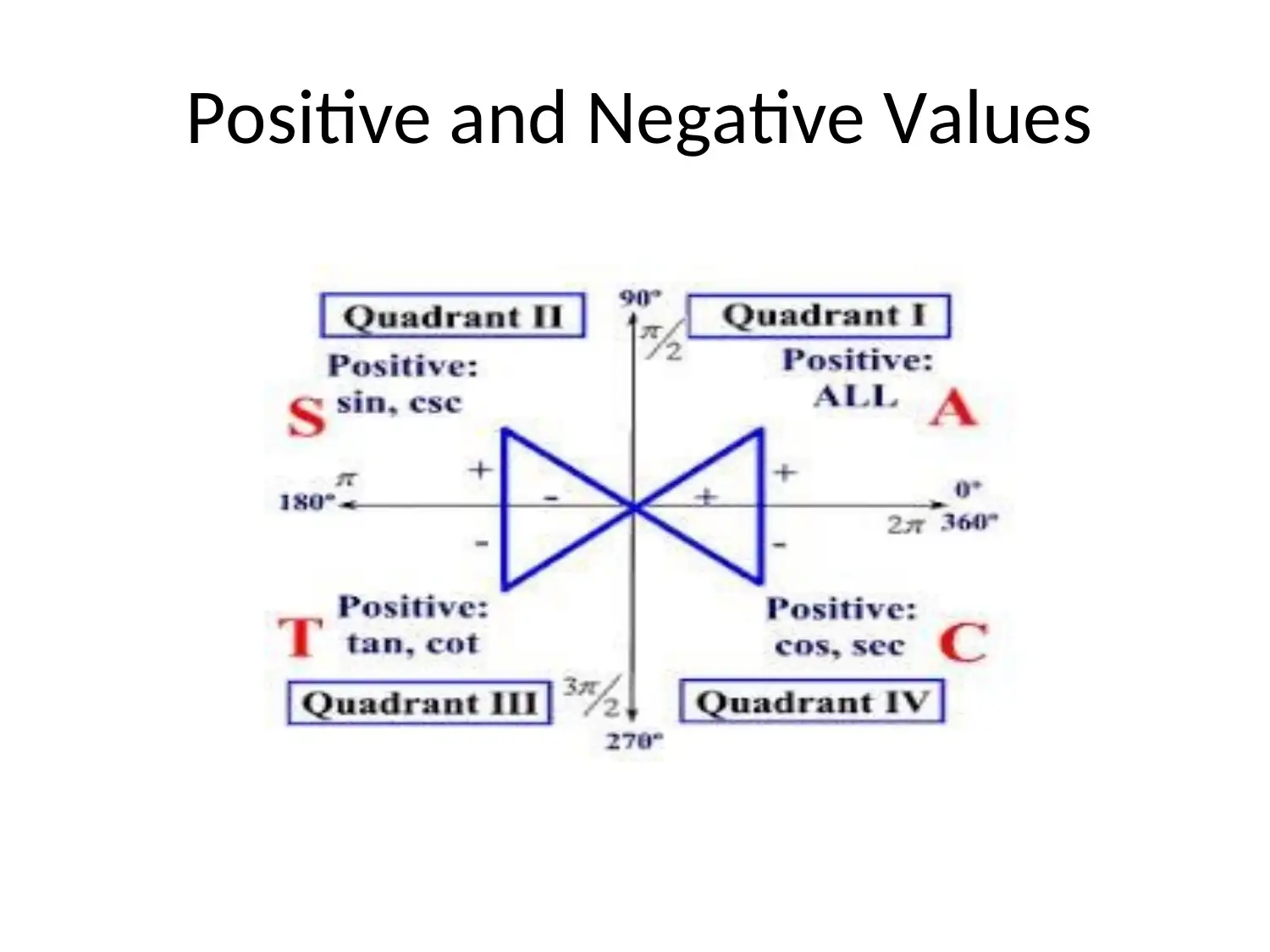
This document provides a thorough introduction to trigonometry, beginning with the basics of triangles and angles, and then delving into the core trigonometric functions: sine, cosine, and tangent. It explains the unit circle, positive and negative values, and the conversion between degrees and radians. The document also covers trigonometric identities, including odd/even, cofunction, and periodicity identities, along with the Law of Sines and the Law of Cosines. Furthermore, it explains how to find missing angles and sides of triangles. It also explores other trigonometric functions like cotangent, secant, and cosecant, providing formulas, identities, and applications, including addition, subtraction, double angle, half-angle, product, and factoring formulas. The content is ideal for students seeking a comprehensive guide to trigonometry, with practical examples and formulas to aid in problem-solving. Desklib is the platform where students can find a wide range of study resources, including past papers and solutions to assist with their assignments.

• Trigonometry ... is all about triangles.
• A triangle has three sides and three angles
• The three angles always add to 180°

Right Angled Triangles
• A right angled triangle is (you guessed it), a
triangle that
has a right angle (90°) in it.
• The little square in the corner tells us that it is
a right angled triangle
(I also put 90°, but you don't need to!)

Names
And we give names to each side:
 Adjacent is adjacent (next to) to the angle θ
 Opposite is opposite the angle θ
 the longest side is the Hypotenuse

"Sine, Cosine and Tangent"
• Trigonometry is good at find a missing side or
angle in a triangle.
• The special functions Sine, Cosine and
Tangent help us!
• They are simply one side of a triangle divided
by another.

For any angle "θ":
Sine Function:
sin(θ) = Opposite / Hypotenuse Cosine Function:
cos(θ) = Adjacent / Hypotenuse Tangent Function:
tan(θ) = Opposite / Adjacent (Sine, Cosine and Tangent are
often abbreviated to sin, cos and tan.)

Example
• What is the sine of 35°?
• Using this triangle (lengths are only to one
decimal place):
• sin(35°) = Opposite / Hypotenuse = 2.8/4.9 =
0.57...

Unit Circle
• It is a circle with a radius of 1 with its center at
0.
• Because the radius is 1, we can directly
measure sine, cosine and tangent.

Positive and Negative Values

Degrees and Radians
• Angles can be in Degrees or Radians. Here are
some examples:
Angle Degrees Radians
Right Angle 90° π/2
Straight Angle 180° π
Full Rotation 360° 2π

Repeating Pattern
• Because the angle is rotating around and
around the circle the Sine, Cosine and Tangent
functions repeat once every full rotation.
• When we need to calculate the function for an
angle larger than a full rotation of 2π (360°)
we subtract as many full rotations as needed
to bring it back below 2π (360°):

Odd/Even Identities
• 1. sin (-x) = -sin x
• 2. cos (-x) = cos x
• 3. tan (-x) = -tan x
• 4. cosec (-x) = -cosec x
• 5. sec (-x) = sec x
• 6. cot (-x) = -cot x

Cofunction Identities - radians
Periodicity Identities - radians
Periodicity Identities - degrees
Cofunction Identity - radians

Example
• what is the cosine of 370°?
• 370° is greater than 360° so let us subtract 360°
• 370° − 360° = 10°
• cos(370°) = cos(10°) = 0.985 (to 3 decimal places)
• And when the angle is less than zero, just add full rotations.
• what is the sine of −3 radians?
• −3 is less than 0 so let us add 2π radians
• −3 + 2π = −3 + 6.283 = 3.283 radians
• sin(−3) = sin(3.283) = −0.141 (to 3 decimal places)

Solving Triangles
• Find the Missing Angle "C“
• Angle C can be found using angles of a triangle
add to 180°
• So C = 180° − 76° − 34° = 70°

Other Functions (Cotangent, Secant,
Cosecant)
• Similar to Sine, Cosine and Tangent, there are three
other trigonometric functions which are made by
dividing one side by another:
• Cosecant Function:
• cosec(θ) = Hypotenuse / Opposite Secant Function:
• sec(θ) = Hypotenuse / Adjacent Cotangent Function:
• cot(θ) = Adjacent / Opposite

The Law of Sines
• The Law of Sines (or Sine Rule) is very useful
for solving triangles:
• It works for any triangle:
• a, b and c are sides.
• A, B and C are angles.
• (Side a faces angle A,
side b faces angle B and
side c faces angle C).

The Law of Cosines
• The Law of Cosines (also called the Cosine
Rule) is very useful for solving triangles:
• It works for any triangle:
• a, b and c are sides.
• C is the angle opposite side c

Exterior Angle Theorem
• For a triangle:
• The exterior angle d equals the angles a plus
b.
• The exterior angle d is greater than angle a, or
angle b.

Value Table

Formulas
• Pythagorean Identities
• Addition Formulas

Formulas
• Subtraction formulas
• Double Angle Formulas

Formulas
• Half-Angle Formulas
• Product Formulas

Formulas
• Factoring Formulas

Quotient Properties:
Reciprocal Properties:

Applications