University Report: ENG-6007B Tuned Circuit and Power Factor Analysis

This technical report details an investigation into tuned circuits and power factor correction. The assignment involves three main parts: estimating the value of an inductor using a designed circuit and frequency variation, designing, building, and testing a tuned filter with a specific resonant frequency and Q factor, and calculating and implementing capacitor-based power factor correction. The report includes circuit diagrams, experimental procedures, results analysis, and discussions on the implications of low industrial power factors and methods for their improvement, such as capacitor banks and synchronous condensers. The work covers the theoretical background, practical implementation, and performance evaluation of these electrical engineering concepts, supported by graphical representations of the experimental data and a discussion on the industrial relevance of power factor correction.

1
Tuned circuit and power factor
Student’s Name
Institutional Affiliation
Date

2
Aims
i) To estimate the value of an inductor
ii) To design, build and test a tuned filter
iii) To calculate the capacitor size needed to correct the power factor of an electrical
circuit and to test the correction
Introduction
An inductor is a simple electrical device that consists of turns of insulated copper wire
wound on a former, with a core made of a material such as soft iron. An inductor is a passive
device that is used in both alternating current and direct current applications. The core can
also be just air as is the case in inductors used for high frequency applications. The action of
an inductor is dependent on the magnetic field that develops within the core and around the
coils as they carry an electric current. The efficiency of an inductor greatly depends on the
material of the core in terms of its ability to concentrate the magnetic fields (Hurley and
Wölfle 2013). Materials that are easily magnetized are the best choices for inductor cores.
The inductor stores energy in its magnetic field. When an electric current flows through the
coils of an inductor, experiments have shown that the voltage developed across the inductor
is proportional to the rate of change of the current with respect to time.
v ∝ di
dt
v=L d i
dt
The constant of proportionality, L is known as inductance and has the unit, Henry. Inductance
can be defined as opposition offered by the inductor to the change of current flowing through

3
it. The value of L depends on many factors such as the physical dimensions of the inductor
and the core material.
A capacitor, on the other hand, is a passive element that is constructed from two
conductors separated by a thin insulating medium called a dielectric. The dielectric medium
varies greatly, from the use of air as the separating medium to electrolytic solutions. This
gives rise to different types of capacitors such as air filled capacitors, electrolytic capacitors
and ceramic capacitors (Damor, 2019). Some capacitors such as electrolytic capacitors have
polarities while others are unpolarised. Unlike an inductor, a capacitor stores energy in its
electric field. According to Bird (2010), capacitors are the most commonly encountered
elements in electronic devices, besides resistors. The application of a potential difference v
across a capacitor develops opposite charges −q andq, on its plates. The stored charge is
directly proportional to the potential difference.
q ∝ v
q=Cv
The constant of proportionality, C is known as capacitance and its unit is the Farad.
Inductors, capacitors, and resistors in AC circuits
Capacitors and inductors can be used in both direct and alternating currents circuits.
However, their responses and analysis in AC circuits are more interesting and complex than
in DC circuits. Capacitors, inductors, and resistors can be combined in parallel or series to
form different types of circuits with different response characteristics in terms of parameters
such as resonance (frequency response). These include RL, RC, LC and RLC parallel and
series connections (Schulz 2010).

4
Power factor and power factor correction
Different electrical loads may require different types of power. Most loads encountered today
such as transformers, motors, and light ballasts are inductive in nature (Batarseh and Wei
2011). According to Clayton (2018), inductive loads demand two types of currents. These
include the real power (working power) needed to carry out the actual task such as motion,
heat generation, and light, and the reactive power which is needed to create and sustain a
magnetic field. Real power is measured in watts while reactive power is measured in VAR
and does not perform any useful work other than circulating between the load and the power
generator. It places a heavier burden on the power supply. Real and reactive power make up
the apparent power. Power factor can be defined as the ratio of real power to apparent power
and is a measure of the effectiveness of the power usage. A high power factor indicates
efficient power utilization whereas a low power factor indicates wastage.
pf = realpower
apparentpower =cosθ
Where θ is the angle between the true and apparent power in the power triangle or the angle
by which the current lags or leads the supply voltage. If the current leads the supply voltage,
the power factor is said to be leading while a lagging current produces a lagging power factor
(Balabanian, 2012). Inductive loads produce lagging power factor while capacitive loads
produce leading power factor.
Part 1
Procedure

5
i) The circuit shown in figure 1 below was designed using a resistor of 1000 Ω and
the inductor whose value was to be determined.
ii) The circuit was then connected to a variable frequency power supply as shown.
iii) Keeping the supply voltage constant, the supply frequency was varied and the
voltage across the resistor recorded
iv) The ratio of the supply voltage to the voltage across the resistor V s
V r
was then
computed and its square ( V s
V r )2
determined for every value of frequency.
v) To determine the value of the inductor ( V s
V r )
2
was plotted against the square of the
frequency to obtain a straight-line plot.
vi) The value of the inductor was then computed from the slope of the graph.
Using Kirchhoff’s voltage law, the supply voltage can be expressed as,
V s =IR+I XL
V s =IR+ I ( 2 πfL )
V s
IR =1+ I ( 2 πfL )
IR
V s
IR = ( 2 πfL )
R +1
But IR=V r
( ( 2 πfL )
R )+1
Squaring both sides, we have,

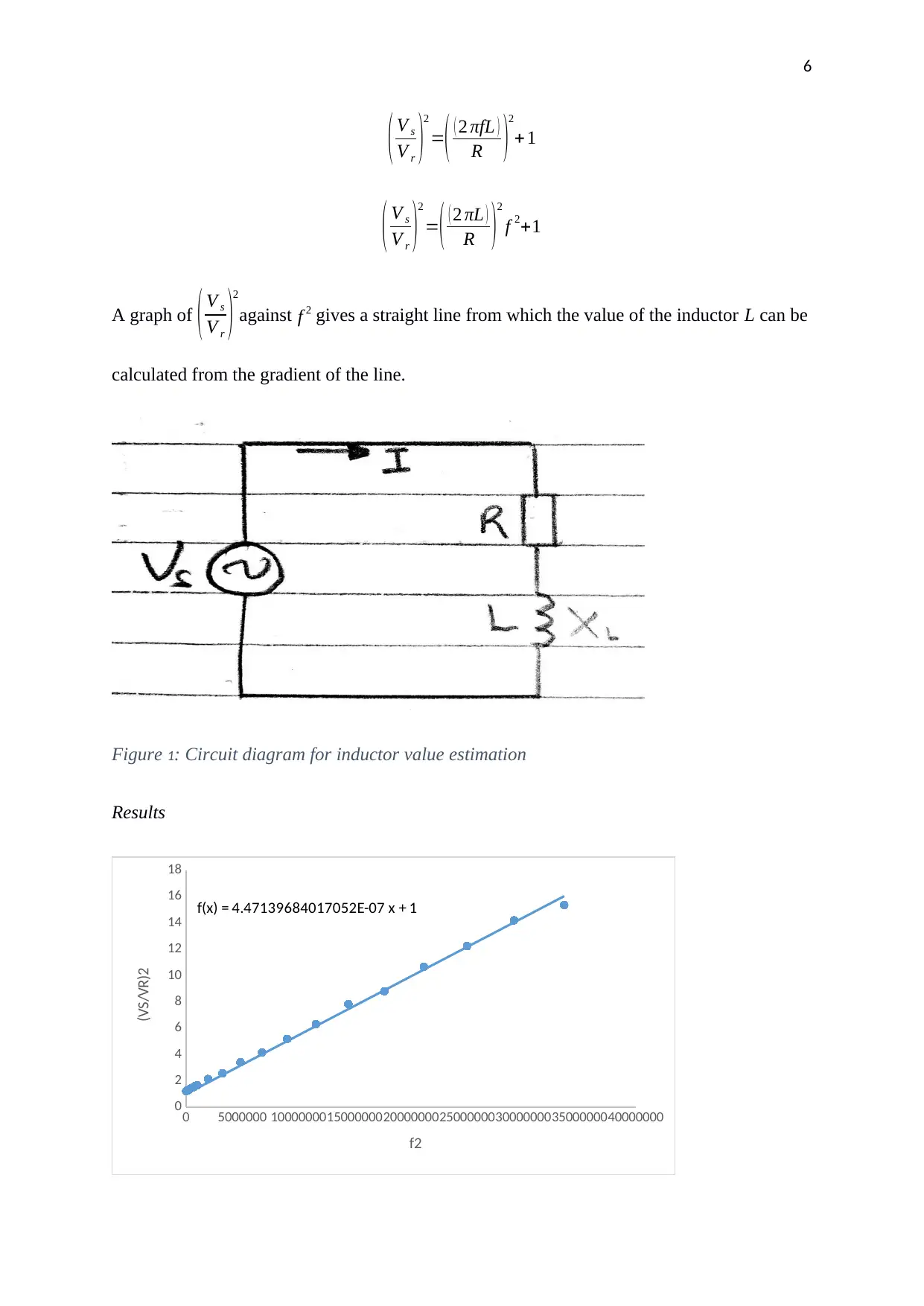
6
( V s
V r )
2
=( ( 2 πfL )
R )
2
+ 1
( V s
V r )
2
=( ( 2 πL )
R )
2
f 2+1
A graph of ( V s
V r )
2
against f 2 gives a straight line from which the value of the inductor L can be
calculated from the gradient of the line.
Figure 1: Circuit diagram for inductor value estimation
Results
0 5000000 10000000150000002000000025000000300000003500000040000000
0
2
4
6
8
10
12
14
16
18
f(x) = 4.47139684017052E-07 x + 1
f2
(VS/VR)2

7
Figure 2: A plot of ( V s
V r )
2
against f 2 to estimate the value of inductance
The graph of ( V s
V r )2
against f 2 yields a straight line as shown in figure 2 above. The equation
of the line is given as,
y=0.00000045 x +1.00000000
Comparing this equation with the equation for a straight line y=m x+c, we have,
y−intercept =1
slope/gradient =0.00000045
Comparing with the circuit equation,
( V s
V r )
2
=( 2 πL
R )
2
f 2+1
Slope=( 2 πL
R )
2
0.00000045=( 2 πL
R )
2
√ 0.00000045= 2 πL
R
L= R √0.00000045
2 π
L=0.1068 H
L=106.8 mH

8
Part 2
Design, build and test of a tuned filter
Components
i) Voltage source
ii) Resistors
iii) Capacitors
iv) Inductor
Procedure
a) The circuit shown in figure 3 below was designed to have a resonant frequency of
5000 Hz and a Q factor of 20. The values of R and C were obtained as follows.
The Q factor of the circuit is given by the following formula,
Q= ωo ∙ L
R
R=ωo ∙ L
Q
L=0.1068 H
ωo=2 πf =2 π × 5000=31415.93 rad /s
R= ( 31415.93 ) ( 0.1068 )
20 =167.76 Ω
The resonant frequency is given by,
ω0= 1
√LC

9
ω0
2= 1
LC
C= 1
L∙ ω0
2
C= 1
( 0.1068 ) ∙ ( 31415 .93 )2 =9.49 nF
Figure 3: Circuit diagram for the tuned filter
R1=81.35Ω
R1=74.88 Ω
C1=4.56 nF
C2=4.55 nF
L=0.1
b) Keeping the supply voltage constant, the supply frequency was varied from 1000
Hz to 50000 Hz and the voltage across the resistor recorded. The ratio of the
magnitude of the voltage across the resistor to the magnitude of the supply voltage

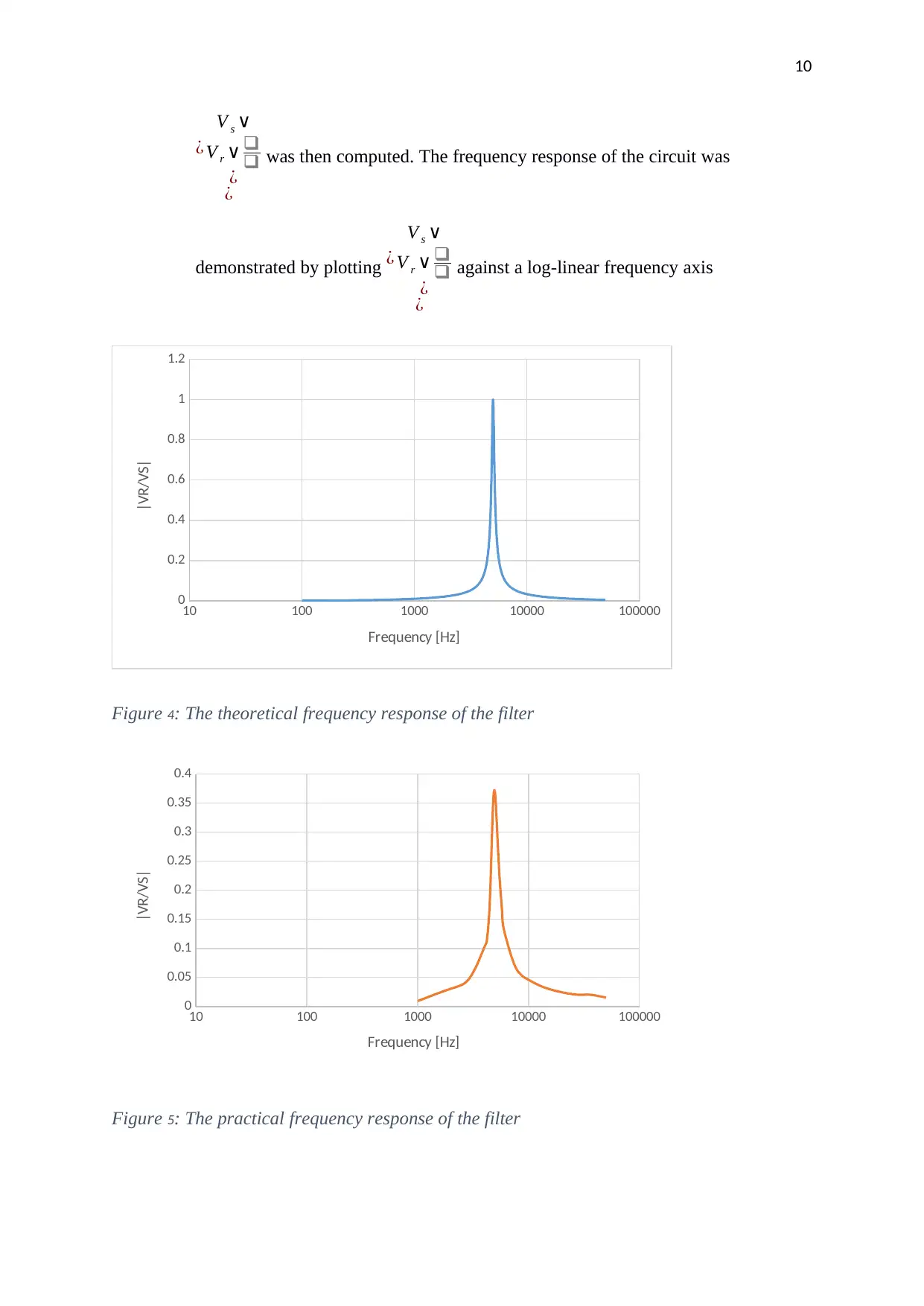
10
¿
V s ∨
V r ∨ ❑
❑
¿
¿
was then computed. The frequency response of the circuit was
demonstrated by plotting ¿
V s ∨
V r ∨ ❑
❑
¿
¿
against a log-linear frequency axis
10 100 1000 10000 100000
0
0.2
0.4
0.6
0.8
1
1.2
Frequency [Hz]
|VR/VS|
Figure 4: The theoretical frequency response of the filter
10 100 1000 10000 100000
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Frequency [Hz]
|VR/VS|
Figure 5: The practical frequency response of the filter

11
c)
i) Below the resonance frequency, the voltage across the resistor lags behind the supply
voltage due to the inductive nature of the circuit.
ii) At the resonance frequency, the circuit is purely resistive. The voltage across the resistor
will be in phase with the supply voltage
iii) Above the resonance frequency, the phase shift increases in the opposite direction and the
two voltages will be almost 180 degrees out of phase.
d) The signal generator was adjusted to give a square wave with a frequency of 1
kHz. The frequency of the output waveform was then measured and compared to
the spectrum of a square wave. The result is shown in figure 6 below.

12
Figure 6: Input and output waveforms from the filter fed with a square wave
e)
LCR band-stop filter
This is a resonant circuit with a capacitor and an inductor in parallel. The parallel combination is then
connected in series with a resistor. The band stop filter only allows a narrow range of frequencies to
pass through while attenuating all the other frequencies.
At resonance,
ω2 LC =1
ω0= 1
√LC
If we select a frequency of 10 kHz and a capacitor with a value of 1 μF
ω0
2= 1
LC
L= 1
C ω0
2

13
1
( 1× 10−6 ) ( 2 π ×10000 ) 2
0.25 mH
Also we have,
Q= ω0 L
R
R=ω0 L
Q
If we select a Q factor of 20,
R= ( 2 π × 10000 ) ( 0.25× 10−3 )
10 =1.57
We choose 1.5 Ω
The parameters of the circuit become,
R=1.5Ω
L=0.25mH
C=1 μF
Part 3
Procedure
a) The circuit of figure 7 below was designed without a capacitor and using the supplied
inductor. The value of the resistor was calculated such that the angle between the
resistive and reactive components was close to 45 degrees.
f =1000 Hz

14
L=0.1 H
The reactive inductance is given by,
X L=2 πfL
( 2 π ) ( 1000 ) ( 0.1 )=628.32
The angle θbetween the reactive and the resistive elements is given by,
tanθ= X L
R
R= XL
tanθ
R=628.32
tan 45
R=628.32
1 =628.32 Ω
Figure 7: The diagram of the circuit with 45 degrees between the reactive and resistive
elements
R1=562.2 Ω
R2=68Ω

15
L=0.1 H
Figure 8: The supply voltage and the voltage across the inductor
b) From theoretical predictions, the value of the capacitor that corrects the power factor
to 1.0 was calculated as follows and inserted into the circuit as shown in figure 9.
From theory, the total impedance Zeq in the circuit should be resistive for the power factor to
be unity.
Zeq=Y +0 j
The circuit’s impedance without a capacitor can be expressed as,

16
Zeq= A+ jB
With a capacitor in parallel the equation becomes,
Zeq= A+ jB /❑ 1
jωC
Zeq= A+ j ( B−ωC A2−ωC B2 )
( 1−ωCB ) 2 ( ωCA ) 2
For Zeq to be purely resistive, the imaginary part must be zero. This occurs when,
B−ωC A2−ωC B2=0
B=ωC A2 +ωC B2=ωC ( A2 +B2 )
ωC= B
A2 + B2
Since we have calculated the value of the resistor,
R=628.32Ω=A
B=ωL= ( 2 π ) ( 1000 ) ( 0.1 )=628.32
ωC= B
A2 + B2 = 628.32
628.322 +628.322 =0.000795773
C= 0.000795773
( 2 π ) ( 1000 )
C=126.65 ×10−9
126.65 nF
The equivalent capacitive reactance is,
X c=1256.64 Ω

17
Figure 9: The circuit diagram for the corrected power factor
C1=100 nF , R1=562.2 Ω
C2=22 nF , R1=68 Ω
C3=4.7 nF
L=0.1 H
c) To investigate the performance of the circuit, figure 10 below was constructed and the
voltages across the capacitor and the input voltages displayed on an oscilloscope. The
photograph is shown in figure 11.

18
Figure 10: The circuit diagram for the corrected power factor testing
R3=562.2 Ω
R3=68Ω
C1=100 nF , R1=562.2 Ω
C2=22 nF , R1=68 Ω
C3=4.7 nF
L=0.1 H

19
Figure 11: The waveforms for the supply voltage and the voltage across the capacitor
d) Implications of low industrial power factors and the way that companies use to deal
with power factor correction
The efficient operation of machinery is one of the greatest concerns in any industrial process
that requires the supply of electricity. The efficient operation of the electrical devices in an
industry depends on its operating power factor (Kouzou, A. (2018). Lower power factors lead
to inefficient and expensive operation since the company has to pay for the extra current
drawn by the machines. According to Waygood (2018), many industrial consumers are
charged additional fees if their power factor is lower than a certain value, for instance, 0.95.

20
In addition, the low power factor lowers the capacity of the electrical distribution system by
increasing the voltage drop and increasing the current flow. The low power factor results
from the mostly inductive loads used in industries such as transformers, high-intensity
discharge lamps, and electric motors. Reactive power forms a major percentage of the total
power consumed by these loads (Yi 2013). In contrast to resistive loads that only dissipate
real power, inductive loads require current to produce a magnetic field. This additional
current constitutes the reactive power which is the nonworking portion. The low power factor
also translates to the need for conductors and machines with higher KVA ratings since the
power factor is inversely proportional to the KVA rating of a machine.
Methods of improving power factor
The disadvantages of low power factor outlined above necessitate the development of
techniques for increasing the power factor towards the ideal value of unity.
i) Use of capacitor banks
Capacitors can be used to lower the inductive power drawn by inductive loads. The reactive
power drawn by an inductive load is always perpendicular to the real power. Capacitors have
the ability to store reactive power and release it to the system, opposing the reactive power
drawn by the load. Consequently, the reactive powers for both the capacitor and the inductor
are 180 degrees opposite to each other. Therefore, the presence of both the inductor and the
capacitor in the system causes the continuous alternating exchange of power between the two
elements, which lowers the current drawn from the generator. In an ideal exchange, all the
power absorbed by the capacitor is equivalent to the power released by the inductor.
ii) Use of synchronous condenser
A synchronous condenser refers to a synchronous motor that is operating in an overexcited
state. Similar to the capacitor, the synchronous condenser draws a leading current hence it

21
can be used for power factor improvement (Khaing, 2014). For correction, the condenser is
normally connected in parallel with the supply, drawing a leading current that partly
neutralizes the reactive component drawn by the load. This technique is rarely used due to the
necessity of a motor starting device and the noise during operation (Channi n.d).
iii) Use of a phase advancer
This device is used to improve the power factor for induction motors. It is usually mounted
on the shaft of the motor. The stator winding draws a lagging current when energized. If the
stator is excited from an external ac supply the power factor can be improved since the
energizing ampere turns are supplied at the slip frequency. Therefore, the reactive power
reduces and the power factor increases (Channi n.d).
Discussion
The aims of this laboratory exercise were to estimate the value of an inductor, to
design a tuned filter and to investigate power factor correction using a capacitor. Like a
capacitor, the reactance of an inductor varies with frequency. Increasing the supply frequency
increases the inductive reactance since the reactance is directly proportional to the frequency
from the formulaX L=2 πfL. This suggests that the value of an inductor can be obtained from
the measurements of the frequency response of a circuit.
A tuned circuit was designed for the given value of frequency and the Q factor. Since
the calculated values of the capacitor and resistor were not among the standard values,
several parallel and series configurations were investigated to closely approximate the
calculated value. The practical frequency response of the circuit was plotted and compared
with the theoretical response. The results are almost similar with the exception that the
theoretical results give a smoother curve. As expected, the maximum magnitude of the

22
response occurs at the resonant frequency of 5000 Hz. However, the maximum response of
the practical response is less than that of the theoretical system. When a square wave was fed
into the circuit, the output was as shown in figure 6. A square wave is basically a summation
of sinusoidal waves. According to Damor (2019), the ideal square wave consists of
components of the form 2 π ( 2 k −1 ) f which are odd-integer harmonic frequencies. The more
the harmonics, the better the square wave approximation. Since our circuit is a filter, it would
eliminate some of the frequencies in the square wave making the output signal more
sinusoidal as it appears in figure 6.
Experiment 3 was done to investigate the effect of a capacitor on the power factor of a
circuit. Since the circuit initially consisted of a resistor and the provided inductor, it was
expected that the inductor would draw a lagging current from the supply, and the voltage
across the inductor would lead the supply voltage by 90 degrees. Therefore, the phase shift
between the input and inductor voltages would be large as shown in figure 8. The magnitude
of the output voltage was slightly less than the input voltage due to the attenuating effects of
the circuit elements. After the circuit was designed for a unity power factor by connecting the
capacitor of the appropriate value across the supply, it was observed that the output voltage
was almost in phase with the supply voltage as shown in figure 7. This shows that the power
factor was improved since theoretically, the output voltage should be in phase with the supply
voltage for maximum power factor.

23
References
Balabanian, N. (2012). Fundamentals of Circuit Theory. NY.
Batarseh, I., and Wei, H. (2011). Power Factor Correction Circuits. Power Electronics
Handbook, 523-547. doi:10.1016/b978-0-12-382036-5.00019-7
Bird, J. (2010). Electrical Circuit Theory and Technology. doi:10.4324/9780080962153
Channi, H.K., (n.d). Overview of Power Factor Improvement Techniques.
Clayton, A. E. (2018). Power Factor Correction: Explaining the Meaning and Importance of
Power Factor, and Describing Methods for the Improvement of Power Factor. NY: Franklin
Classics.
Damor, A. (2019). A. C. Fundamentals, Circuits and Circuit Theory 1. NY.
Hurley, W., and Wölfle, W. (2013). Transformers and Inductors for Power Electronics:
Theory, Design, and Applications. Hoboken, NJ: John Wiley & Sons.
Khaing, M. K. (2014). Power Factor Correction with Synchronous Condenser for Power
Quality Improvement in Industrial Load. International Journal of Science and Engineering
Applications, 3(3), 39-43. doi:10.7753/ijsea0303.1002
Kouzou, A. (2018). Power Factor Correction Circuits. Power Electronics Handbook, 529-
569. doi:10.1016/b978-0-12-811407-0.00017-9

24
Schulz, A. L. (2010). Capacitors: Theory, Types, and Applications. Hauppauge, NY: Nova
Science Pub.
Waygood, A. (2018). Power factor improvement. An Introduction to Electrical Science, 334-
338. doi:10.1201/9781351190435-30
Yi, K. H. (2013). Cost-effective power system design reducing standby power consumption
for the consumer electronic devices. 2013 Twenty-Eighth Annual IEEE Applied Power
Electronics Conference and Exposition (APEC). doi:10.1109/apec.2013.6520752