University Engineering Mathematics Assignment: Comprehensive Problems

This Engineering Mathematics assignment solution covers a range of topics including simplification by division, partial fractions, solving equations, Newton's law of cooling, and geometric progressions. It addresses problems involving the binomial theorem, Maclaurin series, and power series. The document includes detailed calculations, step-by-step solutions, and graphical representations. The assignment explores concepts such as finding the cost of hiring a machine, determining speeds in geometric progression, expanding binomial expressions, and applying Maclaurin's series. The solutions provided offer a comprehensive understanding of the mathematical principles involved and demonstrate the application of these concepts in solving practical problems.

Engineering Mathematics
Student Name:
University
21st January 2018

Task 1:
1) Simplify 6 x2 +7 x−5
x−1 by dividing.
Solution
6 x2 +7 x−5
x−1 = 6 x2+ 10 x−3 x−5
x−1 =2 x ( 3 x +5 )−1(3 x +5)
x−1 = (3 x +5 ) ( 2 x−1 )
x−1 =2(3 x +5)
2) Resolve the following into partial fractions.
a)
x−11
x2 −x−2
Solution
x2−x−2=x2 −2 x + x−2=x ( x−2 ) +1 ( x−2 ) =(x+1)(x−2)
x−11
x2 −x−2 = x−11
( x+1)(x−2)= A
x+1 + B
x −2
x −11
( x +1)( x−2)= A ( x−2 ) + B( x+1)
( x+1)(x−2)
x−11= A ( x−2 ) + B( x+1)
x−11= Ax−2 A + Bx+B
x= Ax+ Bx
A+ B=1
−2 A + B=−11
3 A=12
A=4
4 + B=1
B=−3
Thus the answer is;
A
x+1 + B
x −2 = 4
x +1 − 3
x −2
4
x+1 − 3
x−2
b)

3−x
( x ¿¿ 2+3)(x+ 3)¿
Solution
3−x
( x ¿¿ 2+3)(x+ 3)= A
(x¿ ¿ 2+ 3)+ B
( x +3)+ C
x = A+ B+C
x3 +3 x2+3 x +9 = A+ B+C
x2 ( x +3 ) +3( x +3)= A +B +C
x2 ( x+3 )+3(x+ 3) ¿
¿
3−x
( x ¿¿ 2+3)(x+ 3)=A ( x+3 )+ B (x ¿¿ 2+3)+ Cx
( x ¿¿ 2+3)(x+3) ¿ ¿¿
3−x=A ( x+3 ) + B (x¿¿ 2+3)+Cx ¿
3−x=Ax +3 A + B x2 +3 B+Cx
Ax+2 Bx=−x
A−B=−1
3 A +3 B=3
4 A=2
A=1
2
1
2 −B=−1
B= 3
2
C=1
Thus the answer is;
A
( x ¿¿ 2+3)+ B
(x+ 3)= 1/2
( x ¿¿ 2+3)+ 3 /2
(x +3) ¿
¿
Task 2:
3) We have;
Temp, t(mins) 2 4 6 8 10
Temp 185 161 140 122 106

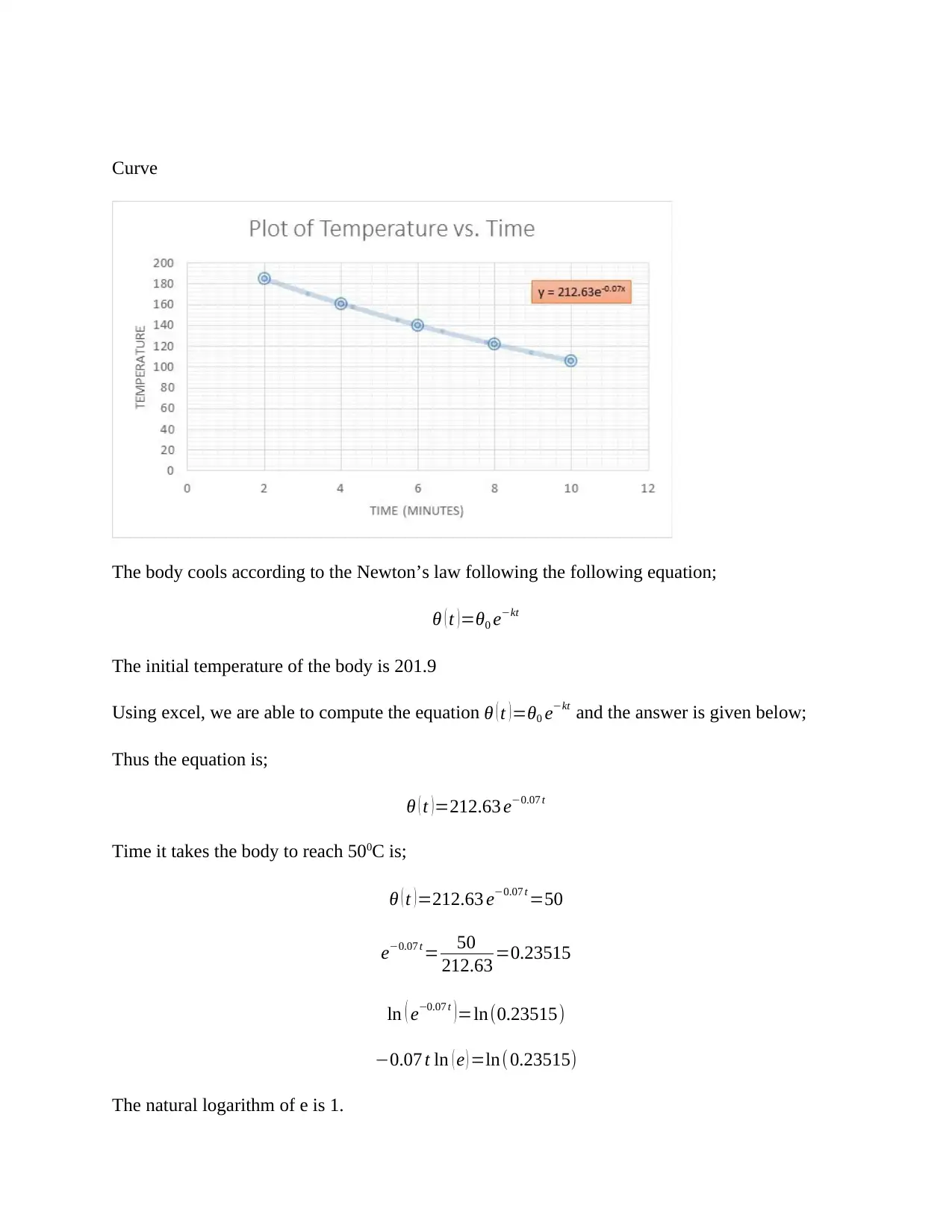
Curve
The body cools according to the Newton’s law following the following equation;
θ ( t )=θ0 e−kt
The initial temperature of the body is 201.9
Using excel, we are able to compute the equation θ ( t ) =θ0 e−kt and the answer is given below;
Thus the equation is;
θ ( t ) =212.63 e−0.07 t
Time it takes the body to reach 500C is;
θ ( t )=212.63 e−0.07 t =50
e−0.07 t = 50
212.63 =0.23515
ln ( e−0.07 t ) =ln(0.23515)
−0.07 t ln ( e ) =ln( 0.23515)
The natural logarithm of e is 1.

−0.07 t=ln(0.23515)
−0.07 t=−1.44753
t=−1.44753
−0.07 =20.67901
Thus it will take 20.679 minutes to reach 500C.
4) Identify, all angles for 0o ≤ θ ≤180o which satisfy the following equation:
sin θ= x
100
Here x is the last two digits of your student number.
Solution
The last two digits of the student number is 40 hence x=40
sin θ= x
100 = 40
100 =0.40
θ=sin−1 (0.40)
θ=23.580 ,156.420
5) A heavy chain under gravity is given by the following equation:
y=50 cosh ( x
100 )
Solve this equation for x when y is 75.
Solution
75=50 cosh ( x
100 )
cosh ( x
100 ) =75
50 =1.5
cosh−1=0.962424
( x
100 )=0.962424
x=96.2424

Second solution is;
cosh−1=2.637576
( x
100 )=2.637576
x=263.7576
Task 3:
6) The annual cost of hiring a machine is £8,000. The contract with the hiring company states
the hiring cost is due to increase by £200 each year. Determine:
a) The cost of hiring the machine during in year 12.
Solution
an=a1 +(n−1)d
a1=8000
d=200
an=12 thterm ; n=12
12 thterm=8000+ ( 12−1 ) 200=8000+2200=10200
Thus the cost of hiring the machine during in year 12 is £10,200
b) How much the machine will have cost in total during the first 15 years.
Solution
Sn= n (a1 +an)
2
a1=8000
an=a15=a1 +(15−1)d
a15=8000+ ( 15−1 ) 200=10800

Sn= n (a1 +an)
2 = 15(8000+10800)
2 =141,000
Thus the total cost in the first 15 years is £141,000
7) A machine is to have seven speeds ranging from 25 rev/min to 500 rev/min. if the speeds
form a geometric progression, determine their value, each correct to the nearest integer.
Solution
First term, a = 25 rev/min
The 7th term is given by: ar7 −1 =500¿ which r6= 500
25 =20∧r=6
√20=1.647549
Hence, 1st term is 25 rev/min
2nd term is ar =25∗1.647549=41.18872
3rd term is a r2 =25∗1.6475492 =67.86044
4th term is a r3 =25∗1.6475493 =111.8034
5th term is a r 4=25∗1.6475494 =184.2016
6th term is a r5 =25∗1.6475495 =303.4811
7th term is a r6 =25∗1.6475496=500
Hence, correct to the nearest whole numbers, the seven speeds are:
25, 41, 68, 112, 184, 303 and 500 rev/min.
Task 4:
8) Use the Binomial Theorem to fully expand ( 2 x−3 y ) 5. Now use the first three terms of the
expansion to estimate the value of ( 2 x−3 y ) 5 when x and y are given by:
a) x=2 , y=0.02
Solution
1 ( 2 x ) 5 ( −3 y ) 0+5 ( 2 x ) 4 ( −3 y ) 1+10 ( 2 x ) 3 ( −3 y ) 2 +10 ( 2 x ) 2 ( −3 y ) 3+5 ( 2 x ) 1 ( −3 y ) 4 +1 ( 2 x ) 0 ( −3 y ) 5
Raise the individual factors to their proper powers.
1 ( 32 x5 ) ( 1 ) +5 ( 16 x4 ) ( −3 y ) + 10 ( 8 x3 ) ( 9 y2 ) +10 ( 4 x2 ) ( −27 y3 ) +5 ( 2 x ) ( 81 y4 ) +1(1)(−243 y5)
This yields;
32 x5 −240 x4 y +720 x3 y2−1080 x2 y3 + 810 x y4−243 y5
Substituting for the first three terms for the values of x and y yields;
32(2)5−240 ( 2 ) 4 0.02+720 ( 2 ) 3 ( 0.02 )2 =949.46944

b) x=5 , y=0.1
Solution
32(5)5−240 ( 5 ) 4 (0.1)+720 ( 5 ) 3 ( 0.1 ) 2=85900
9) Use Maclaurin’s series to determine a power series for e3 x as far as the term in x3.
Solution
The Maclaurin Series of y=ez is
y=1+z + z2
2! + z3
3 ! + z4
4 ! +…
So for y=e3 x where z=3 x we have;
y=1+ ( 3 x ) + ( 3 x ) 2
2! + ( 3 x ) 3
3 ! =1+ 3 x + 9
2 x2 + 9
2 x3
Task 5:
Q1: This expression can be simplified by factoring the numerator. Once the expressions for
the numerator have been factored we then obtain the like terms and divide the like terms.
For instance, we factored ( 3 x+ 5 ) and ( 2 x−1 ) then divided the numerator with ( x−1 ).
This led to the results obtained in Q1 above.
Q2: This question sought to solve what we call partial fraction decomposition. We sought to
find the partial decomposition of P ( x )
Q(x), both Q(x) and P(x) are polynomials of different
degrees with Q(x) having a bigger degree than P(x).
If we have;
Denominator as ax +b then the partial decomposition becomes A
ax+ b
In our case for a), the denominator was of degree 2 while the numerator was degree 1
In b), the denominator was of degree 3 while the numerator was degree 1
Task 6:
Recombining the split partial fractions needs to following steps;
Step 1: Write out the expression using the correct layout.
Step 2: Add the fractions (the same as you would with basic fractions) using the common
denominator (this should always be identical to the original denominator.

Step 3: The denominators are identical so set the numerators equal.
Step 4: Substitute in sensible values of x and/or equate coefficients to create enough
equations to find the values of A, B, C etc.
For example if we have to recombine the following equation;
4
x+1 − 3
x−2
We need to express using the correct layout i.e.
4
x+1 − 3
x−2 = A
x+1 + B
x −2
Add fractions using the common denominator
¿ A ( x −2 )+ B ( x +1 )
( x +1 ) ( x−2 )
Substitute the values
¿ 4 ( x−2 )−3 ( x+1 )
( x+1 ) ( x−2 ) = 4 x−8−3 x−3
( x+1 ) ( x−2 ) = x−11
( x +1 ) ( x−2 )
Task 7:
The power series approach provides quick and direct definitions for a given function as opposed
to e3 x. The benefit of this approach (power series) is that it makes obvious a beautiful connection
between the exponential function and the sine and cosine functions.
Task 8:
Q3:
θ ( t ) =212.63 e−0.07 t
We need to confirm whether this formula works for the different time interval given;
The first time given is 2 minutes we need to plug in to the formula to determine the temperature
at this time;
θ ( 2 ) =212.63 e−0.07 (2)=184.8516 ≈ 185

θ ( 4 )=212.63 e−0.07 (4)=160.7023≈ 161
θ ( 6 ) =212.63 e−0.07(6)=139.7079≈ 140
θ ( 8 ) =212.63 e−0.07(8)=121.4562≈ 122
θ ( 10 ) =212.63 e−0.07 (10)=105.5889 ≈ 106
As can be seen from the above computations, the equation can then be confirmed as true.
Q4:
θvalues were obtained as follows;
θ=23.580 ,156.420
sin θ=sin 23.58=0.400029 ≈ 0.4
Next,
sin θ=sin 156.42=0.400029 ≈ 0.4
From the above confirmations it is evident that the obtained values are the right ones.
Q5:
We have
y=50 cosh ( x
100 )=75
We obtained the value of x to be 96.2424. We need to plug it in and check whether it will
give us y=75.
So we have;
y=50 cosh ( 96.2424
100 )=50 cosh (0.962424)
50 cosh ( 0.962424 )=50∗1.50000039 ≈ 75
This confirms our results
Task 9:
Plotting the graphs;
Q3: We plot the following equation;
θ ( t ) =212.63 e−0.07 t

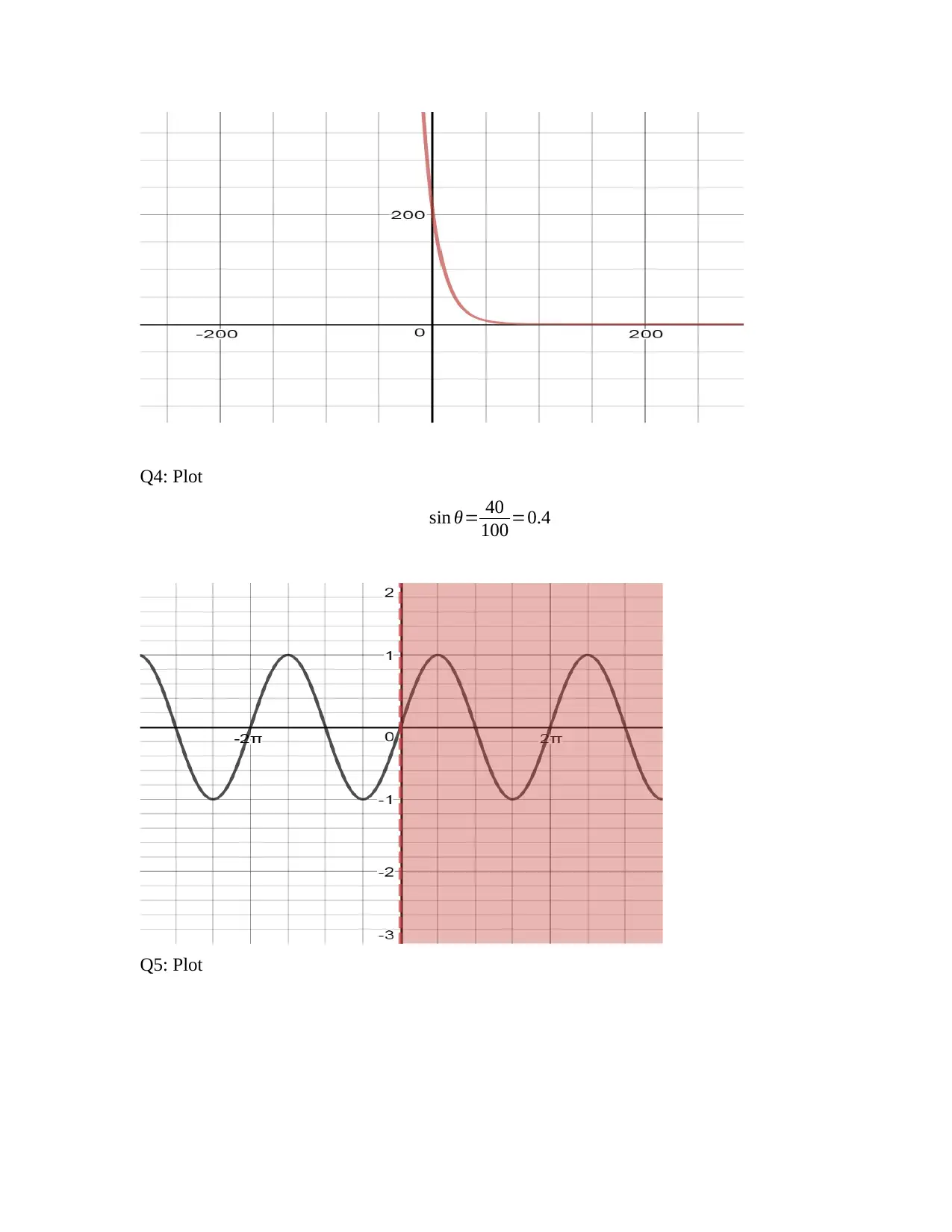
Q4: Plot
sin θ= 40
100 =0.4
Q5: Plot

Task 10:
Yearly increments is 2.25%
Year 1 price is £8,000
Year 2 price is £8,000*1.0225= £8,180
Year 3 price is £8,180*1.0225= £8364.05
As can be seen, this follows a geometric progression with r = 1.0225
The 12th term is given by: ar12−1=8000∗1.022511=10,218.48
Thus the cost of hiring machine in year 12 is £10,218.48
Based on the calculations of task 3 Q6 and this of task 10, we realize that task 10 yields a
slightly higher price than the previous one. It would therefore more profitable for the
company to use it rather than the previous one.