University Mathematics Homework Assignment: Complete Solutions
VerifiedAdded on 2021/04/21
|12
|591
|180
Homework Assignment
AI Summary
This document presents a comprehensive solution to a university-level mathematics assignment. The assignment covers a range of mathematical concepts, including algebraic manipulations, calculations involving percentages and ratios, and functions. Specific problems involve calculating areas, determining sales tax, solving for unknown quantities, and interpreting data. The solutions provide detailed, step-by-step explanations, ensuring clarity and understanding. Additionally, the assignment includes problems related to the domain and range of functions, parabolas, and cost functions, along with financial applications such as calculating interest rates and investment strategies. The document is well-structured, with answers clearly presented and organized by question number and part, making it a valuable resource for students seeking to understand and master the concepts covered in the assignment.

Running head: UNIVERSITY MATHEMATICS
University Mathematics
Name of the student
Name of the university
Author’s note
University Mathematics
Name of the student
Name of the university
Author’s note
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

1UNIVERSITY MATHEMATICS
Table of Contents
Answer 1..........................................................................................................................................2
Part a............................................................................................................................................2
Part b............................................................................................................................................3
Answer 2..........................................................................................................................................3
Part a............................................................................................................................................3
Part b............................................................................................................................................4
Part c............................................................................................................................................4
Part d............................................................................................................................................4
Answer 3..........................................................................................................................................4
Answer 4..........................................................................................................................................4
Part a............................................................................................................................................4
Part b............................................................................................................................................5
Part c............................................................................................................................................5
Table of Contents
Answer 1..........................................................................................................................................2
Part a............................................................................................................................................2
Part b............................................................................................................................................3
Answer 2..........................................................................................................................................3
Part a............................................................................................................................................3
Part b............................................................................................................................................4
Part c............................................................................................................................................4
Part d............................................................................................................................................4
Answer 3..........................................................................................................................................4
Answer 4..........................................................................................................................................4
Part a............................................................................................................................................4
Part b............................................................................................................................................5
Part c............................................................................................................................................5

2UNIVERSITY MATHEMATICS
Answer 1
Part a
(i) ( 5 y2−13 y +17 ) − ( 6 y2 +4 y−13 ) + ( y2−9 y−9 )
¿ 5 y2−13 y +17−6 y2−4 y+13+ y2−9 y−9
¿ 5 y2−6 y2 + y2−13 y−4 y−9 y+17 +13−9
¿−26 y +21
(ii) ( x−2 y )3
× x5 y3
x−2 y7
¿ x−6 y3 X x5 y3
x−2 y7
¿ x−6+ 5+2 y3 +3−7
¿ x y−1
(iii) 12 x3 y4 +8 x5 y3−14 x3 y5
2 x3 y2
¿ 2 x3 y2 X (6 y2+ 4 x2 y −7 y3)
2 x3 y2
¿ 6 y2 +4 x2 y−7 y3
(iv) 12 x
x+1 ÷ 6 x
x2+2 x +1
¿ 12 x
x+1 X x2+ 2 x +1
6 x
¿ 12 x
x+1 X ( x +1 ) 2
6 x
Answer 1
Part a
(i) ( 5 y2−13 y +17 ) − ( 6 y2 +4 y−13 ) + ( y2−9 y−9 )
¿ 5 y2−13 y +17−6 y2−4 y+13+ y2−9 y−9
¿ 5 y2−6 y2 + y2−13 y−4 y−9 y+17 +13−9
¿−26 y +21
(ii) ( x−2 y )3
× x5 y3
x−2 y7
¿ x−6 y3 X x5 y3
x−2 y7
¿ x−6+ 5+2 y3 +3−7
¿ x y−1
(iii) 12 x3 y4 +8 x5 y3−14 x3 y5
2 x3 y2
¿ 2 x3 y2 X (6 y2+ 4 x2 y −7 y3)
2 x3 y2
¿ 6 y2 +4 x2 y−7 y3
(iv) 12 x
x+1 ÷ 6 x
x2+2 x +1
¿ 12 x
x+1 X x2+ 2 x +1
6 x
¿ 12 x
x+1 X ( x +1 ) 2
6 x
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
3UNIVERSITY MATHEMATICS
¿ 2(x +1)
(v) 2+ x
x2 −x − 5
x−1
¿ 2+ x
x( x −1)− 5
x−1
¿ ( 2+ x ) −5 x
x(x −1)
¿ 2−4 x
x(x −1)
2(1−2 x)
x (x−1)
Part b
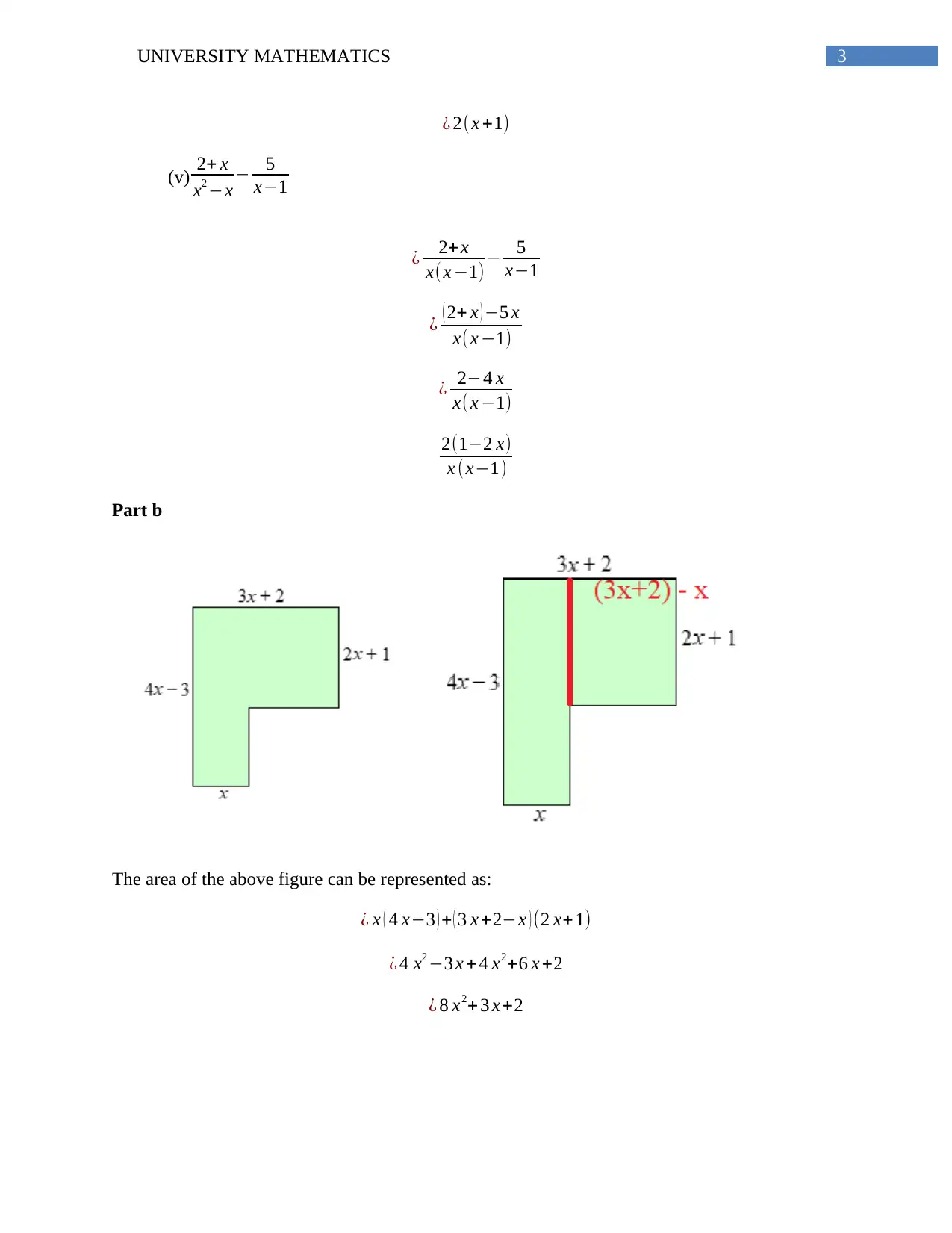
The area of the above figure can be represented as:
¿ x ( 4 x−3 ) + ( 3 x +2−x ) (2 x+ 1)
¿ 4 x2 −3 x + 4 x2+6 x +2
¿ 8 x2+ 3 x +2
¿ 2(x +1)
(v) 2+ x
x2 −x − 5
x−1
¿ 2+ x
x( x −1)− 5
x−1
¿ ( 2+ x ) −5 x
x(x −1)
¿ 2−4 x
x(x −1)
2(1−2 x)
x (x−1)
Part b
The area of the above figure can be represented as:
¿ x ( 4 x−3 ) + ( 3 x +2−x ) (2 x+ 1)
¿ 4 x2 −3 x + 4 x2+6 x +2
¿ 8 x2+ 3 x +2
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

4UNIVERSITY MATHEMATICS
Answer 2
Part a
(i) 4
7 =0.57
(ii) 14
37 =0.38
Part b
The marked price of the dress = RM42
The amount paid to the cashier = RM43.47
Hence, the sales tax on the dress = RM (43.47-42) = RM1.47
On, RM42 the sales tax = RM 1.47
Thus on RM100 the sales tax would be RM 1.47∗100
42 =RM 3.5
Thus, the rate of sales tax is 3.5%
Part c
95% of the questions represent 38 questions
Hence 100% represent 38∗100
95 =40
Hence, the total number of questions in the test were 40
Part d
i. The ratio of Freshman to seniors in 2014 ¿ 40
12 =3.33
ii. The percentage of Sophomores in 2014 = 30%
The total number of students in 2014 = 6542
Hence, the number of Sophomores in 2014 = 6542∗0.3 ≈1963
Considering that the number of Sophomores in 2013 as ‘x’
Hence the number of Sophomores in 2014 would be 1.2x
Hence, according to the problem
Answer 2
Part a
(i) 4
7 =0.57
(ii) 14
37 =0.38
Part b
The marked price of the dress = RM42
The amount paid to the cashier = RM43.47
Hence, the sales tax on the dress = RM (43.47-42) = RM1.47
On, RM42 the sales tax = RM 1.47
Thus on RM100 the sales tax would be RM 1.47∗100
42 =RM 3.5
Thus, the rate of sales tax is 3.5%
Part c
95% of the questions represent 38 questions
Hence 100% represent 38∗100
95 =40
Hence, the total number of questions in the test were 40
Part d
i. The ratio of Freshman to seniors in 2014 ¿ 40
12 =3.33
ii. The percentage of Sophomores in 2014 = 30%
The total number of students in 2014 = 6542
Hence, the number of Sophomores in 2014 = 6542∗0.3 ≈1963
Considering that the number of Sophomores in 2013 as ‘x’
Hence the number of Sophomores in 2014 would be 1.2x
Hence, according to the problem

5UNIVERSITY MATHEMATICS
1.2 x=1963
x ≈ 1636
Thus, the number of sophomores in 2013 would have been 1636
iii. The central angle = 360o
The percentage of juniors = 18%
Thus, the central angle for juniors = 360o∗18
100 =64.8o
Answer 3
Part a
i. f ( x )= 5
2 x−4
The domain is not defined for x = 2, since at 2, f(x) = 5
0 which is undefined.
Thus, the domain of f(x) = all real numbers except 2
The range of f(x) = all real numbers except 2
1.2 x=1963
x ≈ 1636
Thus, the number of sophomores in 2013 would have been 1636
iii. The central angle = 360o
The percentage of juniors = 18%
Thus, the central angle for juniors = 360o∗18
100 =64.8o
Answer 3
Part a
i. f ( x )= 5
2 x−4
The domain is not defined for x = 2, since at 2, f(x) = 5
0 which is undefined.
Thus, the domain of f(x) = all real numbers except 2
The range of f(x) = all real numbers except 2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
6UNIVERSITY MATHEMATICS
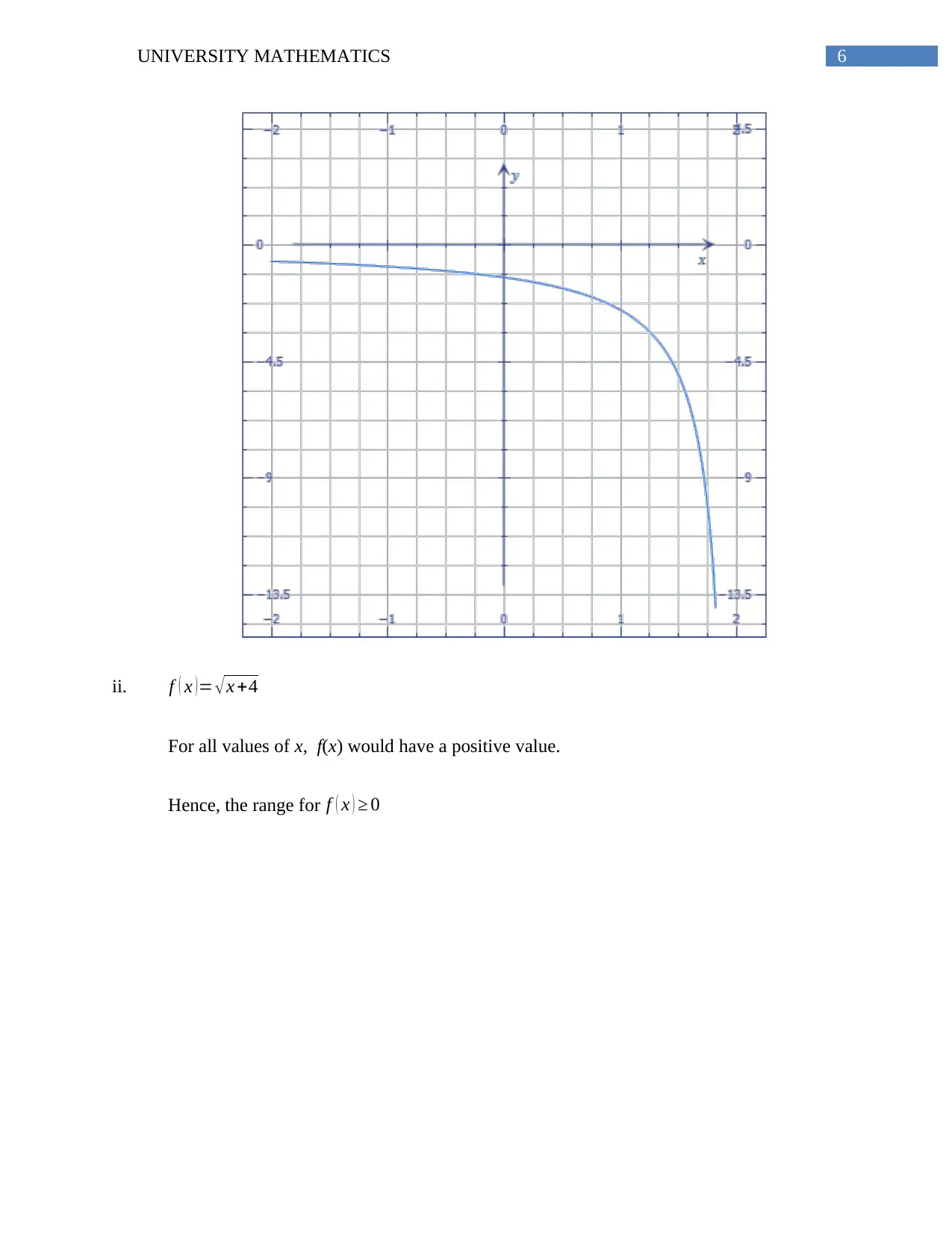
ii. f ( x )= √x +4
For all values of x, f(x) would have a positive value.
Hence, the range for f ( x ) ≥ 0
ii. f ( x )= √x +4
For all values of x, f(x) would have a positive value.
Hence, the range for f ( x ) ≥ 0
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
7UNIVERSITY MATHEMATICS
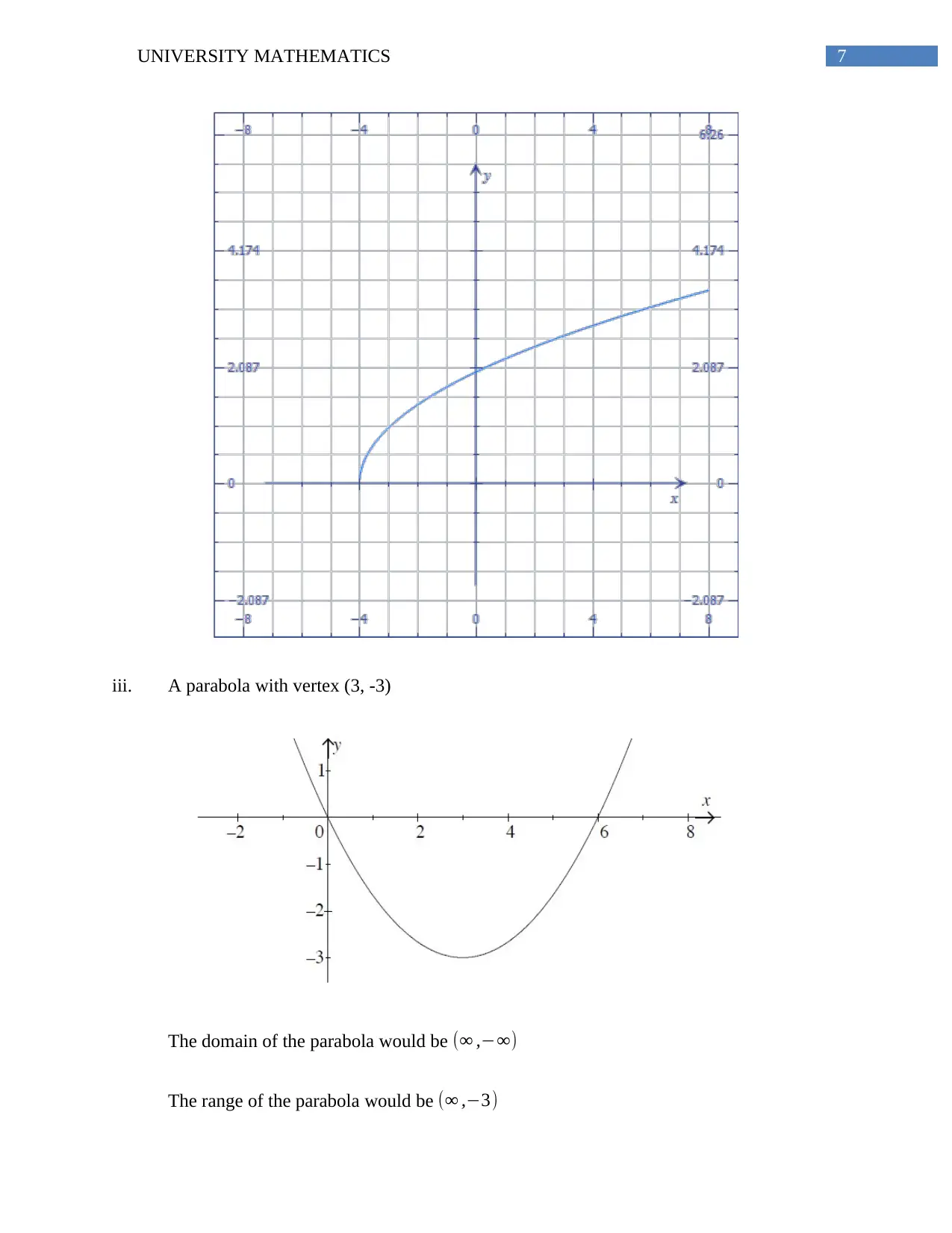
iii. A parabola with vertex (3, -3)
The domain of the parabola would be (∞ ,−∞)
The range of the parabola would be (∞ ,−3)
iii. A parabola with vertex (3, -3)
The domain of the parabola would be (∞ ,−∞)
The range of the parabola would be (∞ ,−3)

8UNIVERSITY MATHEMATICS
Part b
f ( x )=x2 +1
g ( x )= 1
x2 +1
i. f ( g ( x ) )= ( 1
x2 +1 )2
+1= x4 +2 x2+ 2
x4 +2 x2+ 1
ii. g ( f ( x ) ) = 1
( x2 +1 )
2
+1 = 1
x4 +2 x2+2
Part c
i. n=P (t )=75 t −2 t2
C ( n ) =7 n+1000
C ( n ) =7∗( 75 t−2t2 ) +1000=1000+525t−14 t2
The cost in terms of number of number of hours of assembly line functioning is:
C ( n )=1000+525 t−14 t2
ii. The number of hours of assembly functioning = 12
Hence, the cost of the bicycle = 1000+525∗12−14∗122=1000+6300−2016
¿ 5284
Answer 4
Part a
(i)
x= 2± √ ( −2 ) 2−4∗1∗2
2∗1
x= 2± √4−8
2
x= 2± √−4
2 = 2± 2 √−1
2
x=1 ± √−1=1± i
Part b
f ( x )=x2 +1
g ( x )= 1
x2 +1
i. f ( g ( x ) )= ( 1
x2 +1 )2
+1= x4 +2 x2+ 2
x4 +2 x2+ 1
ii. g ( f ( x ) ) = 1
( x2 +1 )
2
+1 = 1
x4 +2 x2+2
Part c
i. n=P (t )=75 t −2 t2
C ( n ) =7 n+1000
C ( n ) =7∗( 75 t−2t2 ) +1000=1000+525t−14 t2
The cost in terms of number of number of hours of assembly line functioning is:
C ( n )=1000+525 t−14 t2
ii. The number of hours of assembly functioning = 12
Hence, the cost of the bicycle = 1000+525∗12−14∗122=1000+6300−2016
¿ 5284
Answer 4
Part a
(i)
x= 2± √ ( −2 ) 2−4∗1∗2
2∗1
x= 2± √4−8
2
x= 2± √−4
2 = 2± 2 √−1
2
x=1 ± √−1=1± i
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
9UNIVERSITY MATHEMATICS
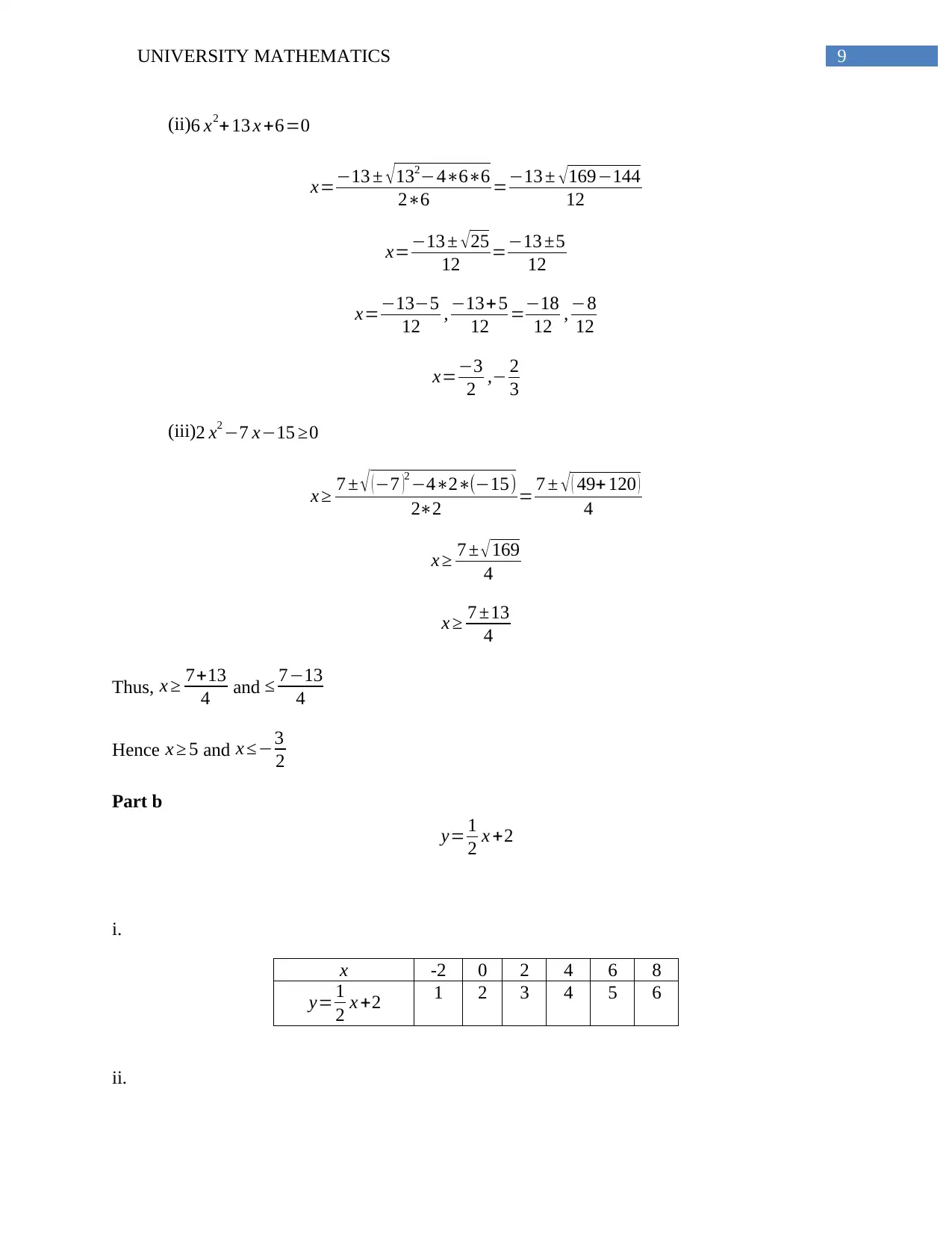
(ii)6 x2+ 13 x +6=0
x=−13 ± √132−4∗6∗6
2∗6 =−13 ± √169−144
12
x=−13 ± √25
12 =−13 ±5
12
x=−13−5
12 , −13+ 5
12 =−18
12 , −8
12
x=−3
2 ,− 2
3
(iii)2 x2 −7 x−15 ≥0
x ≥ 7 ± √ ( −7 )
2 −4∗2∗(−15)
2∗2 = 7 ± √ ( 49+ 120 )
4
x ≥ 7 ± √169
4
x ≥ 7 ±13
4
Thus, x ≥ 7+13
4 and ≤ 7−13
4
Hence x ≥ 5 and x ≤−3
2
Part b
y= 1
2 x +2
i.
x -2 0 2 4 6 8
y= 1
2 x +2 1 2 3 4 5 6
ii.
(ii)6 x2+ 13 x +6=0
x=−13 ± √132−4∗6∗6
2∗6 =−13 ± √169−144
12
x=−13 ± √25
12 =−13 ±5
12
x=−13−5
12 , −13+ 5
12 =−18
12 , −8
12
x=−3
2 ,− 2
3
(iii)2 x2 −7 x−15 ≥0
x ≥ 7 ± √ ( −7 )
2 −4∗2∗(−15)
2∗2 = 7 ± √ ( 49+ 120 )
4
x ≥ 7 ± √169
4
x ≥ 7 ±13
4
Thus, x ≥ 7+13
4 and ≤ 7−13
4
Hence x ≥ 5 and x ≤−3
2
Part b
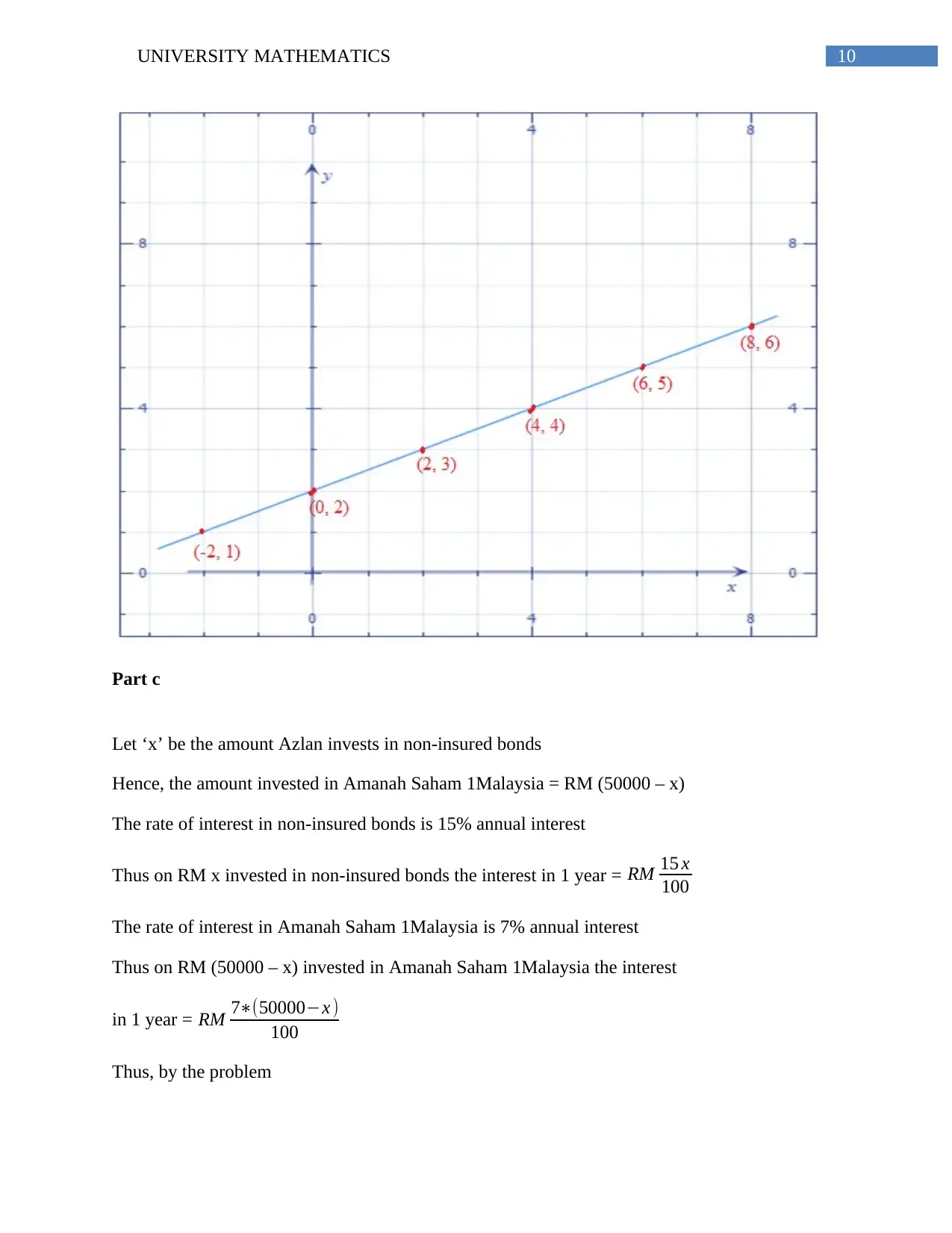
y= 1
2 x +2
i.
x -2 0 2 4 6 8
y= 1
2 x +2 1 2 3 4 5 6
ii.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
10UNIVERSITY MATHEMATICS
Part c
Let ‘x’ be the amount Azlan invests in non-insured bonds
Hence, the amount invested in Amanah Saham 1Malaysia = RM (50000 – x)
The rate of interest in non-insured bonds is 15% annual interest
Thus on RM x invested in non-insured bonds the interest in 1 year = RM 15 x
100
The rate of interest in Amanah Saham 1Malaysia is 7% annual interest
Thus on RM (50000 – x) invested in Amanah Saham 1Malaysia the interest
in 1 year = RM 7∗(50000−x )
100
Thus, by the problem
Part c
Let ‘x’ be the amount Azlan invests in non-insured bonds
Hence, the amount invested in Amanah Saham 1Malaysia = RM (50000 – x)
The rate of interest in non-insured bonds is 15% annual interest
Thus on RM x invested in non-insured bonds the interest in 1 year = RM 15 x
100
The rate of interest in Amanah Saham 1Malaysia is 7% annual interest
Thus on RM (50000 – x) invested in Amanah Saham 1Malaysia the interest
in 1 year = RM 7∗(50000−x )
100
Thus, by the problem

11UNIVERSITY MATHEMATICS
15 x
100 + 7∗(50000−x )
100 =6000
15 x+ 350000−7 x=6000∗100=600000
8 x=600000−350000=250000
Hence, x=31250
Thus, Azlan should invest in RM 31250 in non-insured bonds
And RM18750 in Amanah Saham 1Malaysia
15 x
100 + 7∗(50000−x )
100 =6000
15 x+ 350000−7 x=6000∗100=600000
8 x=600000−350000=250000
Hence, x=31250
Thus, Azlan should invest in RM 31250 in non-insured bonds
And RM18750 in Amanah Saham 1Malaysia
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 12
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




