Vehicle Dynamics and Control: Vibration, Damping and PID Project

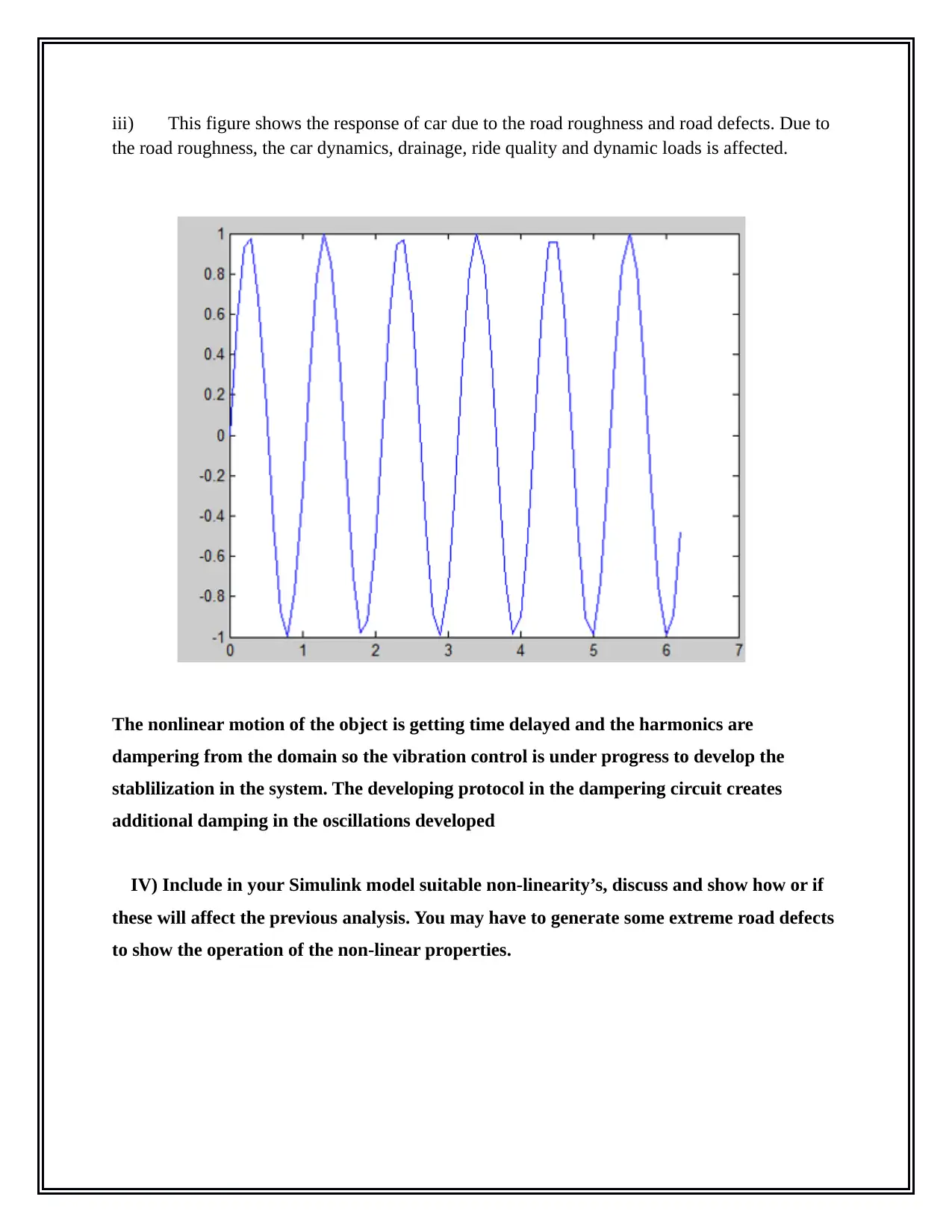
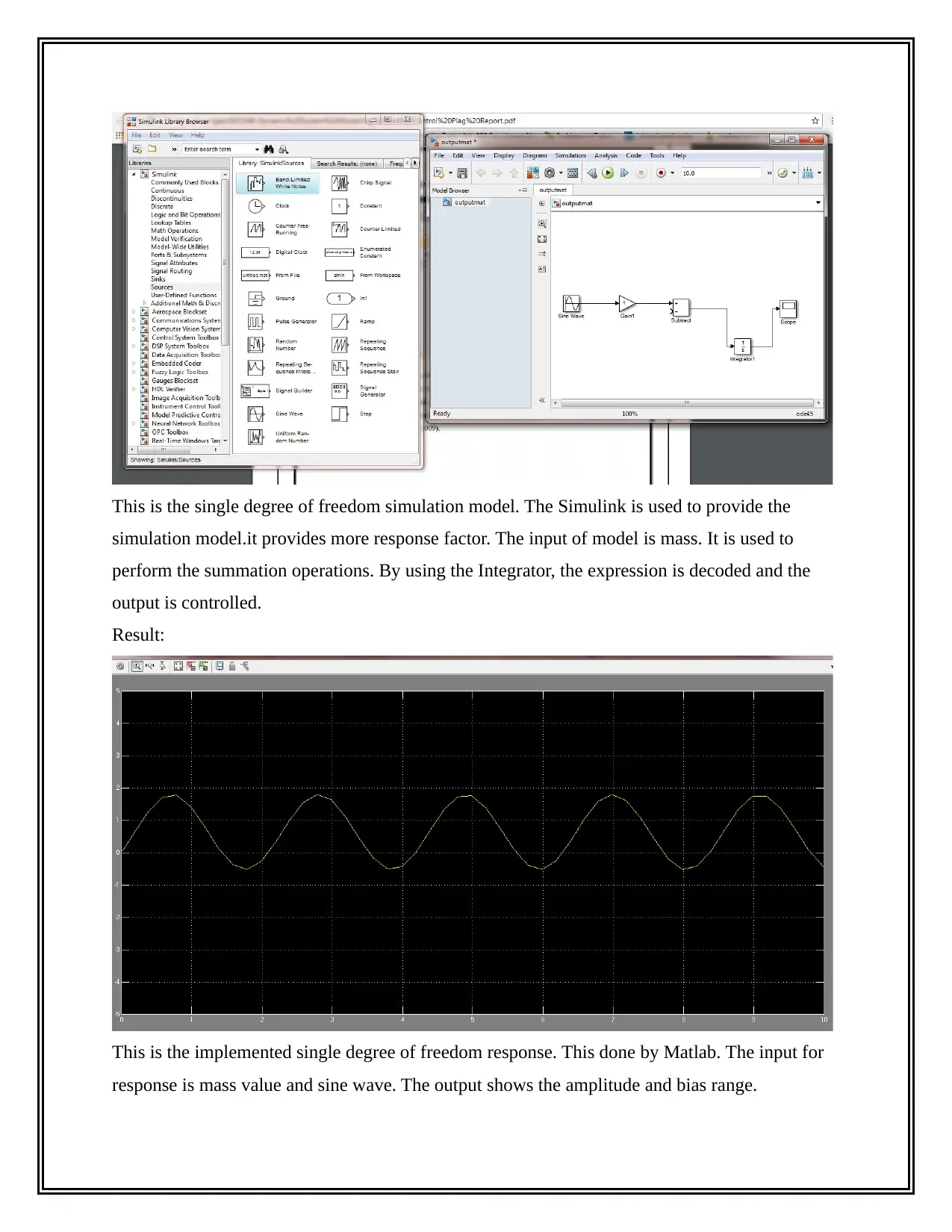
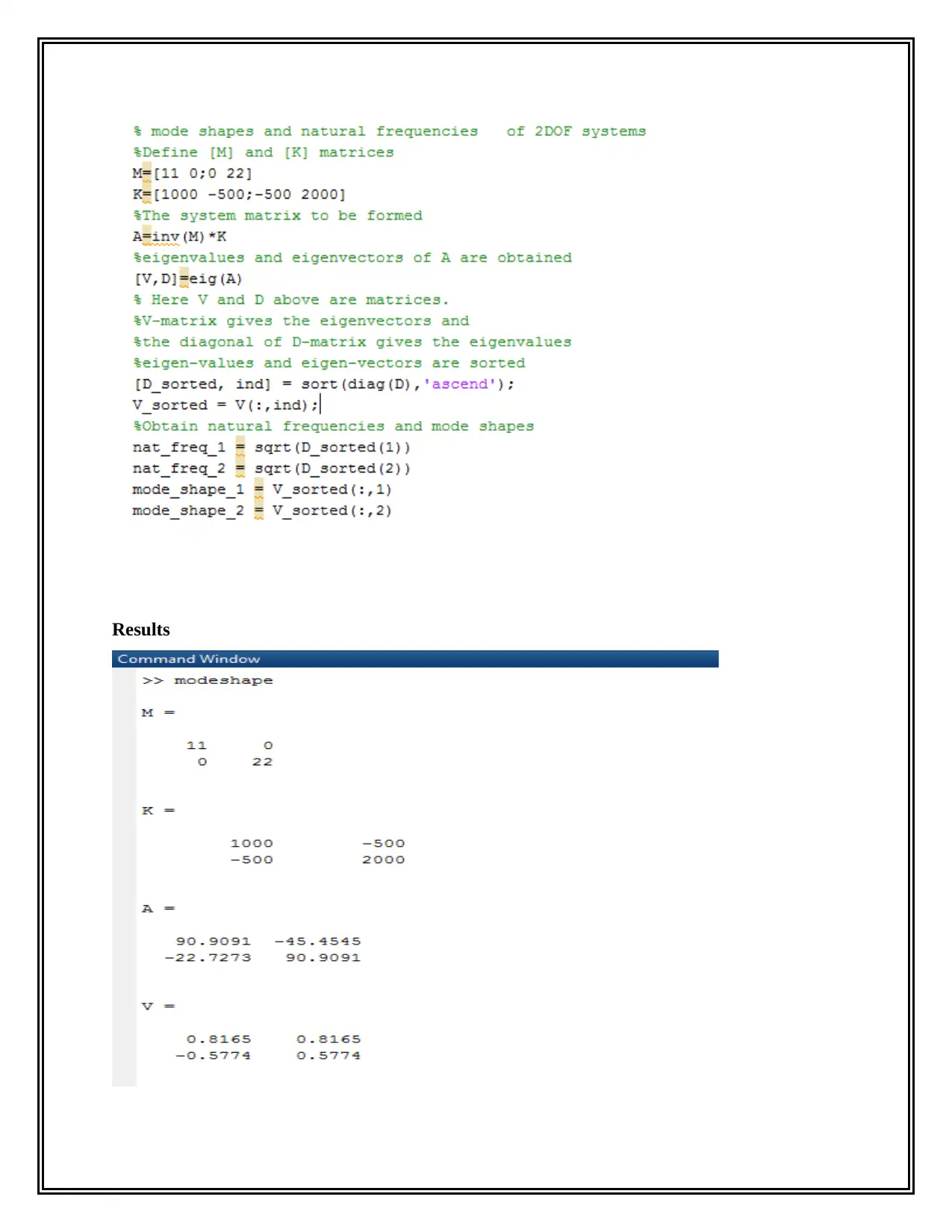
This project analyzes vehicle dynamics, focusing on free and forced vibrations in single and two-degree-of-freedom (DOF) systems. It explores the effects of damping on vehicle performance, including where high and low damping are beneficial and how damping levels affect passenger comfort and wheel-road contact. The project includes a Simulink model with non-linearities and discusses their impact on the analysis. It also covers the simulation and analysis of a PID controller, exploring different parameter values and their effects on system stability and performance. Furthermore, the project demonstrates brake control operation and analyzes the stability of a cruise control system, discussing its disadvantages and potential improvements. Finally, the project derives equations of motion, calculates free and forced vibration responses, critical damping, and the magnification factor for a rotating system, expressing these in terms of relevant parameters. The project provides a comprehensive understanding of vehicle dynamics, control systems, and their practical applications.

DEMONSTRATION PROBLEMS
i) For free vibration
After the first vibration, the system meets its own disturbance, that vibration is called as free
vibration. The free vibrations are represented by homogeneous Ordinary Differential Equations.
The Types of free vibration of single degree of freedom systems
1. harmonic motion,
2. Free vibration of undamped SDOF systems,
3. Free vibration of damped SDOF systems
ii) For forced vibration
If any external force is applied to the system, the reaction of the system is called as forced
vibration. The frequency of the system is matched with external force frequency, it leads to
heavy oscillation because of the occurred resonance. The forced vibrations are represented by
Non homogeneous Ordinary Differential Equations.
Types of forced vibration of single degree of freedom systems
1. Harmonic excitation
2. Base excitation

iii) This figure shows the response of car due to the road roughness and road defects. Due to
the road roughness, the car dynamics, drainage, ride quality and dynamic loads is affected.
The nonlinear motion of the object is getting time delayed and the harmonics are
dampering from the domain so the vibration control is under progress to develop the
stablilization in the system. The developing protocol in the dampering circuit creates
additional damping in the oscillations developed
IV) Include in your Simulink model suitable non-linearity’s, discuss and show how or if
these will affect the previous analysis. You may have to generate some extreme road defects
to show the operation of the non-linear properties.

This is the single degree of freedom simulation model. The Simulink is used to provide the
simulation model.it provides more response factor. The input of model is mass. It is used to
perform the summation operations. By using the Integrator, the expression is decoded and the
output is controlled.
Result:
This is the implemented single degree of freedom response. This done by Matlab. The input for
response is mass value and sine wave. The output shows the amplitude and bias range.

The development of the system enhances the domain in the single degree of freedom
response and this MATLAB is enhanced with the development of the idea in the tenangrad
of the sinusoidal output where the region of the stabilization takes place
v) Damping helps to isolating vibration and reduces transmitted vibration. Based on your
analysis write a paragraph on the effect of damping in affecting your car’s performance i.e.
Where would be better to use high damping; Where would it be better to use low damping;
and how does the damping levels you have chosen in your car affect passenger comfort and
the wheel road contact force.
Damping is major features of noise proofing an existing or fresh wall structure.
Damping is used to decreasing or avoiding kept energy shaped by sound. If a structure has
low damping, sound vibration can travel across it for great distances. The tires have the
automobile characteristics of handling and ride. It has the reaction point of vehicle at the
roadway. It has ability to manage the problem at the road. Because it is the final link from the
driver. The springs, linkages and dampers are used to manage the tires basic functions. The
damping is used to control the spring effect in the vehicle (vibration).Damping is used to
compare engineering material for the applications. High damping is used in vibration control,
reducing increased heat, and shock absorption and noise control. Low damping is used for
increasing sensitivity in sensors and definite accuracy instrumentation.
In the increasing sensitivity of the the module due to heat and other mass related transfer
functions the newton’d Raphson model is included and the research have been developed
to control the shock absorption and other damping oscillations of the accuracy
transmissions.

i)Two equation of motion is
m1 ´x1 +(c1 +c2 ) ´x1−c2 ´x2 +(k1 +k2 ) x1−k2 x2=F1
m2 ´x2 +(c1+ c2 ) ´x2−c2 ´x1+(k2 +k 3) x2 −k2 x1=F2
ii)Equation of motion in matrix form
[m] ´
x
→
(t)+[c] ´
x
→
(t)+[k ] x
→
(t)=F
→
(t )
Here,
[m]is the mass matrix
[c ]is the damping matrix
[k ]is the stiffness matrix
X ( t)is the displacement vector
F (t)is the force vector
[m]=[m1 0
0 m2
] [c ]=[c1 +c2 −c2
−c2 c1 +c2
] [k ]=[k1 +k2 −k2
−k2 k2 +k3
]
iii) To finding the Natural frequecies and mode shaping using the eigen values and eigrn vectors
in matlab is shown in below code.
Matlab code:

Results

iv) The natural frequencies and mode shape of 2DOF from the matlab output, the two degree
of freedom system has two normal modes of vibration corresponding to the two natural
frequencies.
v) The vibration solution for 2DOF in road surface
Matlab code

Result

vi) In 2DOF modelling the natural frequencies and mode shapes are analysed.The multiple
degree of freedom will be investigated by using this 2DOF modelling in future analysis.

Simulation of PID controller for m=100,c=1000,k=5000
Result