WMAT123 Term 2 2019 Assignment 2: Mathematics Solutions

This document presents the solutions to Assignment 2 for Mathematics 123, a course offered at Macquarie University International College. The assignment covers a range of mathematical topics, including finding the highest common factor (HCF) of polynomials using the rational roots theorem and Euclid's algorithm, solving exponential and logarithmic equations, applying differentiation using first principles and the power rule, analyzing a quartic function to find its equation, stationary points, and bi-tangent, and investigating a cubic function to find its stationary points, points of inflection, x-intercepts, and global extrema within a specified domain. Each question is solved step-by-step, demonstrating the application of various mathematical concepts and techniques to arrive at the final answers. The solutions are presented in a clear and organized manner, providing a comprehensive guide to understanding and solving the assignment problems.

Assignment – 2
Mathematics 123
<Student name>
MACQUARIE UNIVERSITY INTERNATIONAL COLLEGE
APRIL 18, 2019

Question 1
This question investigates the highest common factor of two polynomials. All
polynomials are assumed to be monadic (i.e. having the leading coefficient of 1)
Consider the two polynomials
p ( x )=x5−7 x4 +31 x2 +65 x +150
q ( x ) =x5 +x4 −18 x3−41 x2−83 x −60
a) Assuming a rational root, use the rational roots theorem to discover a common
linear factor to both 𝑝(𝑥) 𝒂𝒏𝒅 𝑞(𝑥).
Sol.
HCF ( p ( x ) , q ( x ) )
p(x )=x5−7 x4 +31 x2 +65 x +150
p ( x )=(x +2)( x4−9 x3 +18 x2−5 x+75)
p ( x )=(x +2)( x−5)( x3−4 x2 −2 x−15)
p ( x )=(x +2)( x−5)(x−5)(x2+x +3)
q ( x ) =x5 +x4 −18 x3−41 x2−83 x −60
q ( x )= ( x −5 ) ( x4 +6 x3 +12 x2+19 x +12 )
q ( x )= ( x −5 ) (x +1) ( x3+ 5 x2 +7 x+ 12 )
Highest linear common factor=x−5
b) Divide this linear factor into both polynomials to simplify the problem of finding
the highest common factor.
Sol.
p ( x )=(x +2)( x−5)(x−5)(x2+x +3)
q ( x )= ( x −5 ) ( x4 +6 x3 +12 x2+19 x +12 )
c) Adapt Euclid’s algorithm for numbers to find the highest common factor of
𝑝(𝑥)𝑎𝑛𝑑 𝑞(𝑥). For this, you can take the highest common factor of the reduced
polynomials found in (b) and multiply by the common linear factor found in (a)
Sol.
p ( x)
q( x )= ( x+ 2)(x−5)( x−5)( x2 +x+ 3)
( x−5 ) ( x +1) ( x3 +5 x2 +7 x +12 )
p ( x)
q( x )= (x +2)( x−5)( x2+ x +3)
( x +1) ( x3 +5 x2 +7 x +12 )
Question 2

Find all solutions to the following equations:-
a) 22 x +1=512
Sol.
22 x +1=512
22 x +1=29
2 x+1=9
x=4
b) 3 x+ 1
4 x +1 = x −2
x+ 2
Sol.
3 x+1
4 x +1 = x −2
x+2
( 3 x+ 1 ) ( x +2 ) = ( 4 x +1 ) ( x−2 )
3 x2+7 x +2=4 x2−7 x−2
x2−14 x−4=0
x= 14 ± √ (−14 )2−4 ( 1 ) (−4 )
2 ( 1 )
x= 14 ± √196+ 16
2
x= 14 ± √212
2
x= 14 ± 14.56
2
x=14.28∨x=−0.28
c) 6 log2
3
√ x−log2 ( x+3 ) =4
Sol.
6 log2
3
√ x−log2 ( x+3 )=4
6 log2 x
1
3 −log2 ( x+3 )=4
6
3 log2 x−log2 ( x +3 )=4
2 log2 x −log2 ( x +3 ) =4
log2 x2−log2 ( x+3 ) =4
log2
x2
x +3 =log2 16
x2
x+3 =16
x2−16 x−48=0
x= 16 ± √ (−16 )2−4 (1)(−48)
2(1)

x= 16 ± √256+192
2
x= 16 ± √448
2
x= 16 ±21.16
2
x= 16+21.16
2 ∧x= 16−21.16
2
x=18.58∧x=−2.58
d) x−1
3 − x +3
4 =2 x−1
Sol.
4 x−4−3 x−9=24 x−12
x−13=24 x−12
23 x=−1
x=−1
23
Question 3
a) Differentiate using first principles f ( x )=x2 +3 x+ 5
Sol.
y=x2 +3 x+5
dy
dx =2 x +3
b) Differentiate the following functions:
i. g ( x ) =x3−x2−12 x
Sol.
y=x3−x2−12 x
dy
dx =3 x2 −2 x−12
ii. h ( x ) = ( x2 +x+ 1 ) ( x3−2 x2 +4 x −1 )
Sol.
y= ( x2 +x +1 ) ( x3−2 x2 +4 x−1 )
y=x5−2 x4 + 4 x3−x2+ x4−2 x3+ 4 x2−x + x3−2 x2 +4 x−1
y=x5−x 4+3 x3 + x2+ 3 x −1
dy
dx =5 x4−4 x3+9 x2 +2 x+3
iii. k ( x )= x2 +2 x +3
x5+3 x2−2 x−1

Sol.
y= x2 +2 x+3
x5+ 3 x2−2 x−1
dy
dx = ( x5 +3 x2−2 x−1 ) ( 2 x +2 ) +(x2 +2 x+3)(5 x4 +6 x−2)
( x5 +3 x2−2 x−1)2
iv. p ( x ) = ( 20 x19−19 x20 ) 2019
Sol.
y= ( 20 x19−19 x20 )2019
dy
dx =2019(380 x18−380 x19 )2018
Question 4
Consider the quartic y=x4 +b x3 + c x2+ dx+ewhich has stationary points where
x=−1,0∧2 and has a y-intercept at 10.
a) Calculate the values of 𝑏, 𝑐, 𝑑, 𝑒 and hence find the equation of the quartic.
Sol.
y=x4 +b x3 + c x2+ dx+e
dy
dx =4 x3 +3 b x2+ 2cx + d
Given dy
dx =0 at x=−1,0∧2
dy
dx ¿ x=−1
=4 (−1)3 +3 b (−1)2 +2 c (−1 ) + d
dy
dx ¿ x=−1
=−4+ 3 b−2 c +d

−4+3 b−2 c+d=0 … … … ( 1 )
dy
dx ¿ x=0
=4 ( 0 )3 +3 b ( 0 ) 2+ 2c ( 0 ) +d
d=0 … … … ( 2 )
dy
dx ¿ x=2
=4(2)3 +3 b(2)2 +2 c ( 2 ) +d
dy
dx ¿ x=2
=32+12 b+4 c +d
32+12 b+4 c+ d=0 … … … ( 3 )
¿ Eq ( 1 ) , Eq ( 2 )∧Eq ( 3 )
3 b−2 c=4∧12 b+ 4 c=−32
3 b−2 c=4∧3 b+c=−8
4 +2 c=−8−c
12=−3 c
c=−4
b=−4
3
Given y¿ x=0=10
e=10
Equation of quartic is given by :
y=x4 +b x3 + c x2+ dx+e
y=x4 − 4
3 x3−4 x2 +10
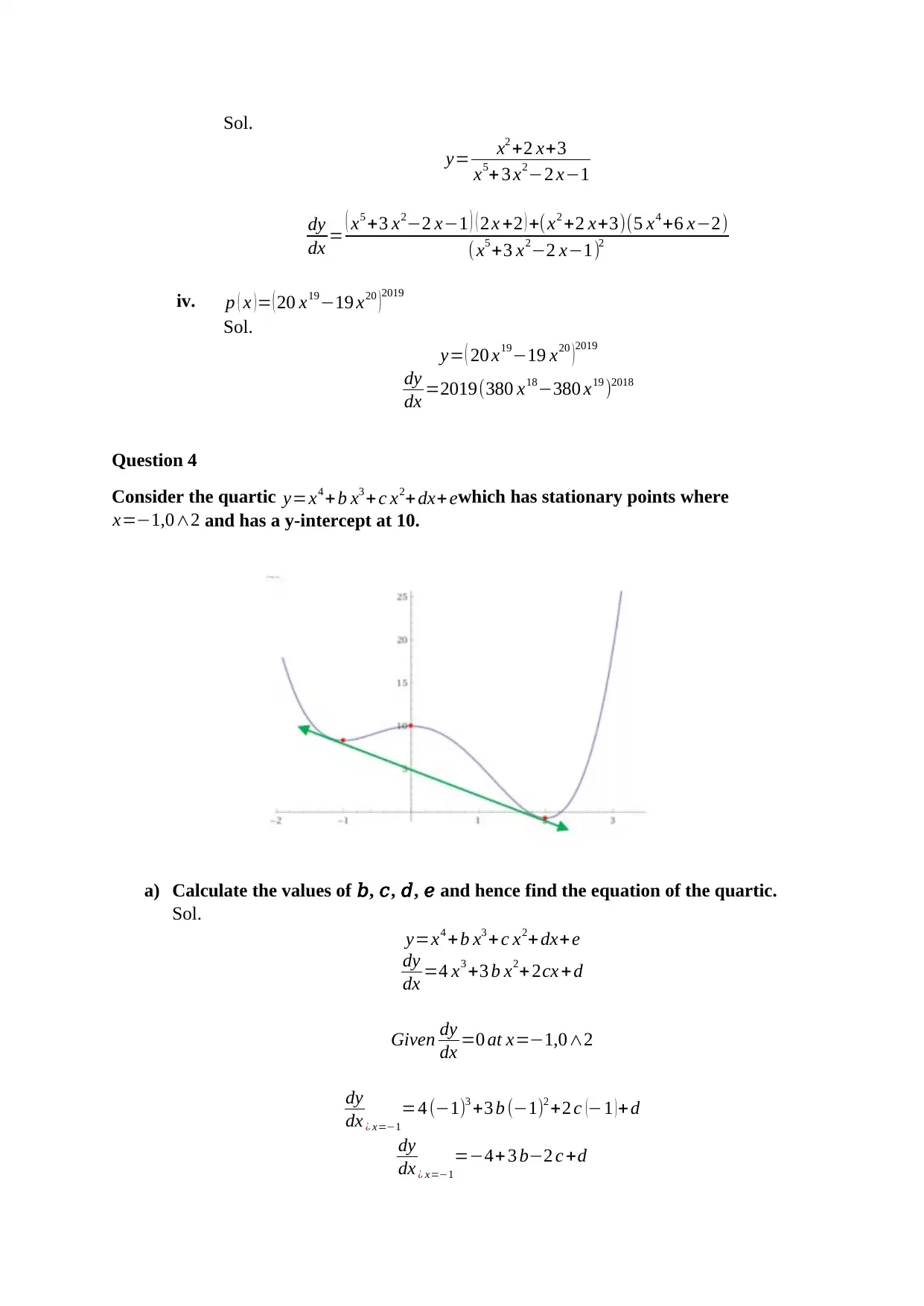
b) A bi-tangent is a line that is a tangent to the curve twice. Illustrated is the graph
of the quartic and its bi-tangent. Calculate the equation of the bi-tangent.
(Hint: Let the line have equation 𝑦 = 𝑚𝑥 + 𝑏. The points of contact with curve the
are each double roots! (NB: The points of contact are NOT the stationary points
themselves)
Sol.
The bitangent passes throughthe points x=−1∧x=2
y¿ x=−1=(−1)4− 4
3 (−1 )3−4 (−1 )2 +10
y¿ x=−1=1+ 4
3 −4 +10
y¿ x=−1=7+ 4
3

y¿ x=−1= 25
3
P(−1 , 25
3 )
y¿ x=2=(2)4 − 4
3 ( 2 )3−4 ( 2 )2+10
y¿ x=2=16− 4
3 .8−16+10
y¿ x=2=10− 32
3
y¿ x=2=−2
3
Q(2 ,− 2
3 )
The line y=mx+b passes through points P∧Q
25
3 =m ( −1 ) + b∧−2
3 =m ( 2 ) + b
3 b−3 m=25∧6 m+3 b=−2
25+3 m=−2−6 m
27=−9 m
m=−3
b=16
3
Equation of bitangent :
y=−3 x + 16
3
3 y +9 x−16=0
Question 5
Consider the curve y=x3−4 x2 +2 x +3
a) Find all the stationary points of the curve.
Sol.
For all the stationary points
dy
dx =0

dy
dx =3 x2 −8 x+2=0
Using the quudratic formula
x=−b ± √ b2−4 ac
2 a
Substituting a=3 , b=−8∧c =2
x= 8 ± √(−8)2−4 (3)(2)
2(3)
x= 8 ± √64−24
6
x= 8 ± √40
6
x= 8 ±6.32
6
x= 8+6.32
6 ∧x= 8−6.32
6
x= 14.32
6 ∧x=1.68
6
x=2.38∧x=0.28
b) Determine the nature of the stationary points found.
Sol.
¿ find the nature of the stationary points found
We have ¿ find d2 y
d x2
d2 y
d x2 = d
dx ( 3 x2−8 x +2 )
d2 y
d x2 =6 x−8
d2 y
d x2
¿ x=2.38
=6 ( 2.38 ) −8
d2 y
d x2
¿ x=2.38
=6.28
∵ d2 y
d x2
¿x=2.38
is positive ,∴ x=2.38 is a minima
d2 y
d x2
¿ x=0.28
=6 ( 0.28 ) −8
d2 y
d x2
¿ x=0.28
=−6.32

∵ d2 y
d x2
¿x=0.28
is negative ,∴ x=0.28is a maxima
c) Check for any points of inflexion on the curve. (Be sure to show the change in
concavity either side)
Sol.
¿ ˇthe point of inflexion ,
d2 y
d x2 =0
d2 y
d x2 =6 x−8
6 x−8=0
x= 8
6
x=1.33
y¿ x=1=13−4 ( 1 ) 2+ 2 ( 1 ) +3
y¿ x=1=1−4+2+3
y¿ x=1=2
y¿ x=2=23−4 ( 2 ) 2 +2 ( 2 ) +3
y¿ x=2=8−16+4 +3
y¿ x=2=−1
There isno point of inlexion∈the given function
d) Given that at least one of the x-intercepts is rational, determine all x intercepts of
this curve.
Sol.
x−intercept of the curve can be found at y=0
y=x3−4 x2 +2 x +3
y=0
x3−4 x2+2 x+ 3=0
( x−3 ) ( x2−x−1 ) =0
x−3=0∨x2−x −1=0
x=3∨x=1 ± √ 1−4 ( 1 ) ( −1 )
2 ( 1 )
x=3∨x=1 ± √5
2
x=3∨x=1.62∨x=−0.62
x−intercepts :
( 3,0 ) , ( 1.62,0 ) ∧(−0.62,0)
e) Find the global minimum and global maximum when the domain for the
function is restricted to [0,4]
Sol.
There ∃only one minima∧one maxima ∈therange [ 0,4 ]

∴ x=0.28 isthe global maxima∧¿
x=2.32 isthe global minima of the function
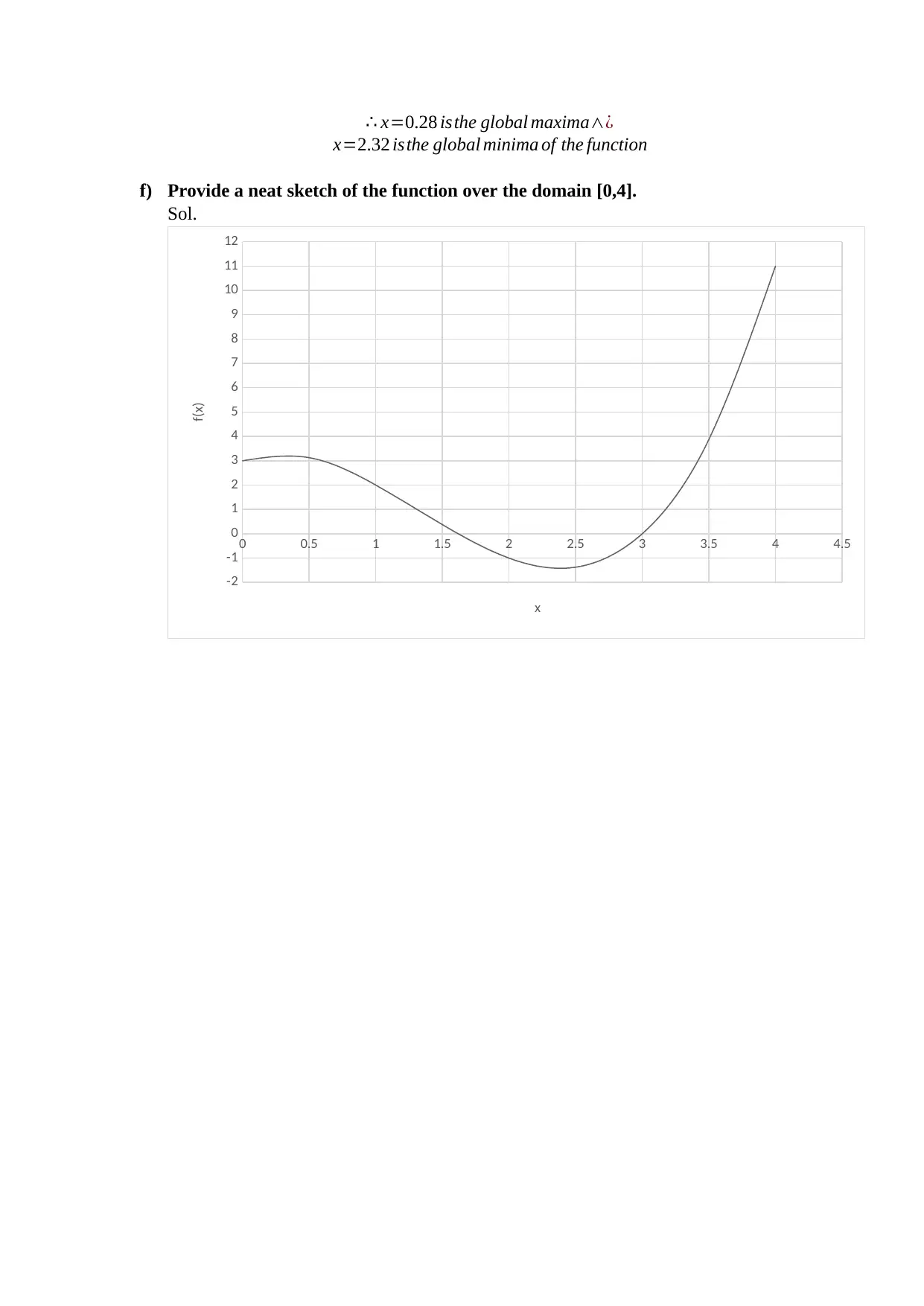
f) Provide a neat sketch of the function over the domain [0,4].
Sol.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-2
-1
0
1
2
3
4
5
6
7
8
9
10
11
12
x
f(x)