MAT2002 Lab Assignment 05: Z-Transforms and Difference Equations

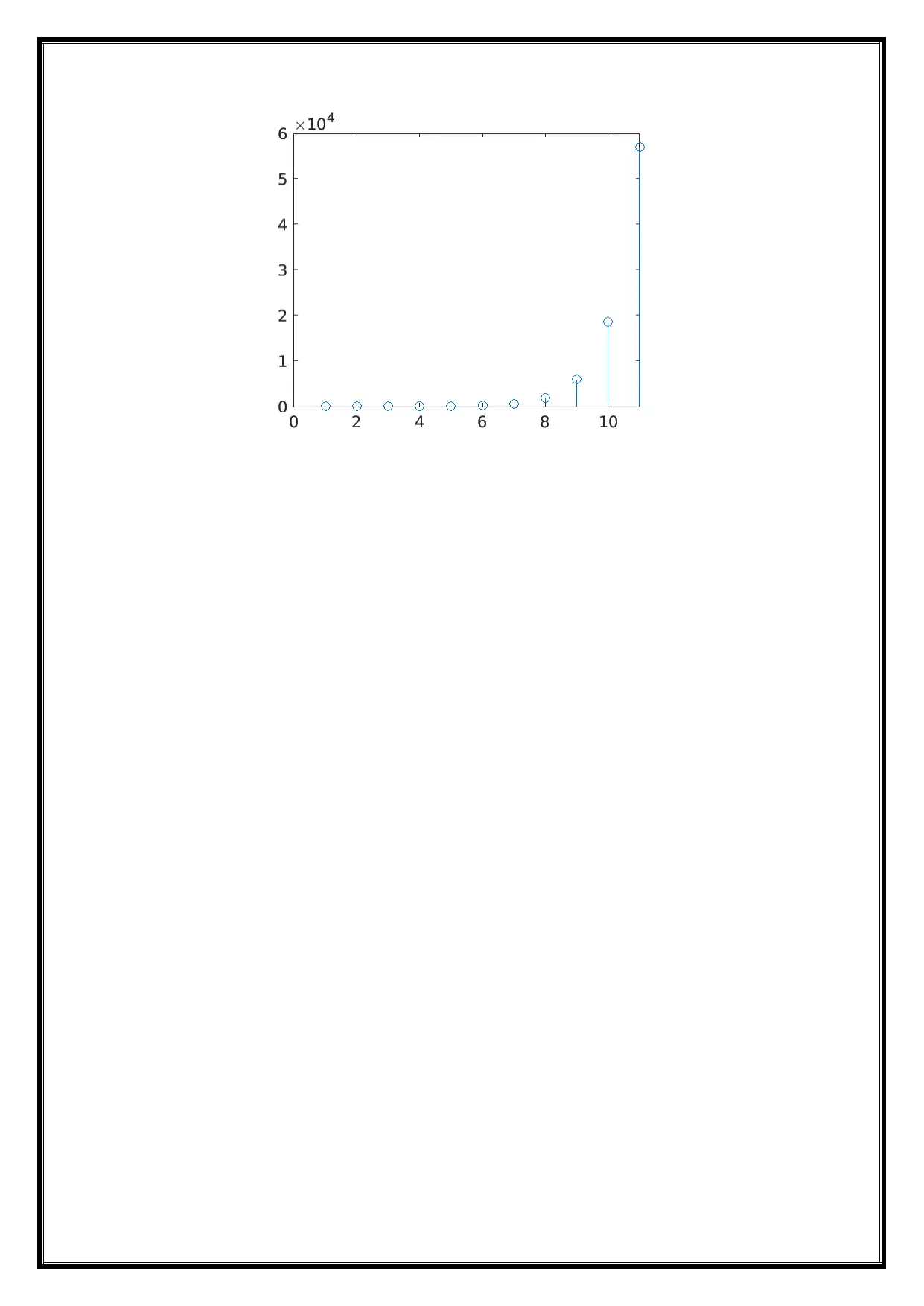
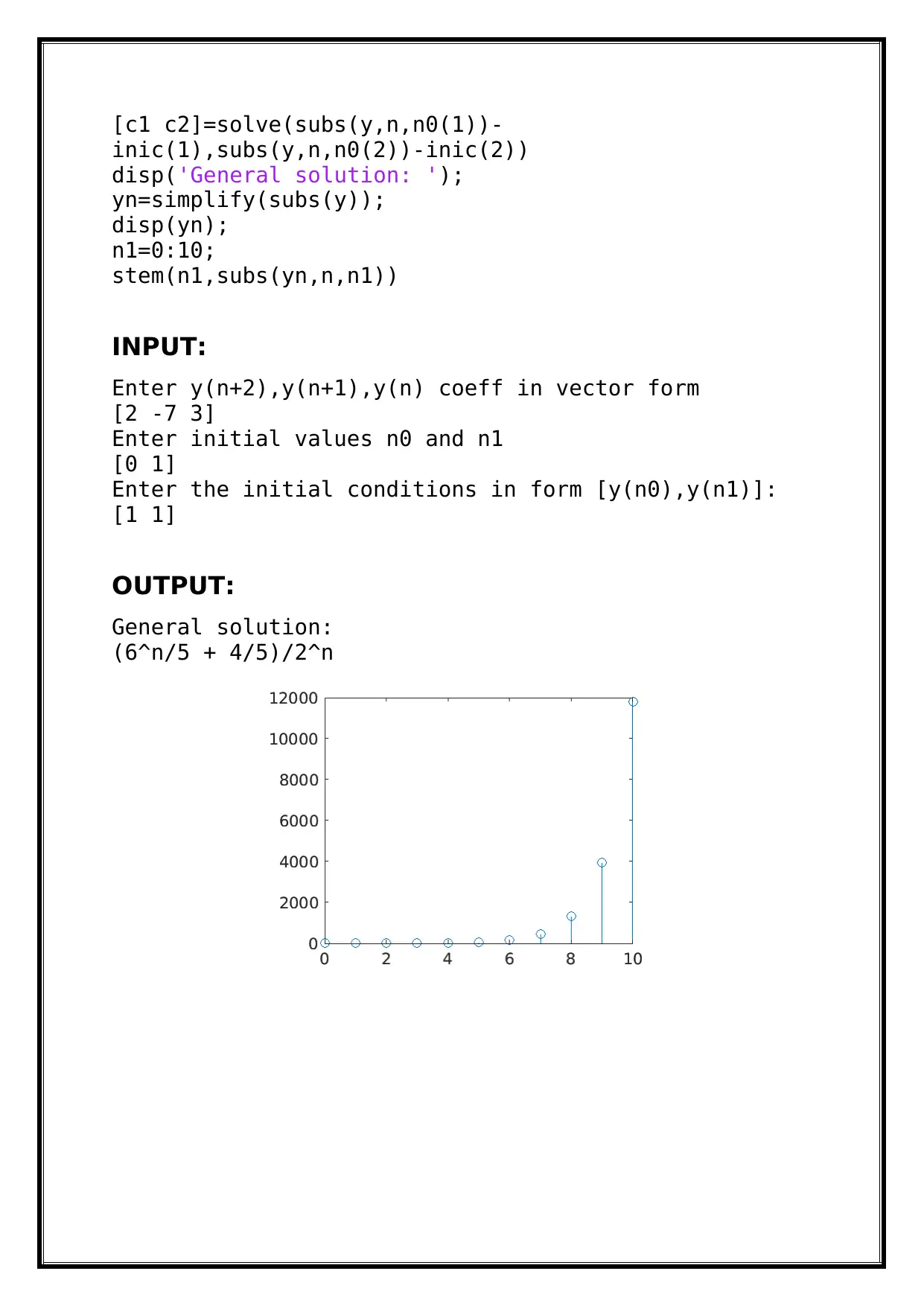
This document presents a solution to MAT2002 Lab Assignment 05, focusing on the applications of differential and difference equations. The assignment covers two main experiments. The first experiment, 5A, utilizes Z-transforms to solve a non-homogeneous difference equation, providing the MATLAB code, input, and output, and then plots the solution. The second experiment, 5B, addresses the solution of homogeneous linear difference equations. This section includes the MATLAB code, input, and output, and covers the general solution based on the roots of the characteristic equation, considering cases for distinct, repeated, and complex roots and plots the solution. The assignment emphasizes the use of MATLAB for solving and visualizing the solutions of difference equations with specific initial conditions.

APPLICATIONS OF DIFFERENTIAL
AND DIFFERENCE EQUATIONS –
MAT2002
LAB ASSIGNMENT – 05
NAME: S. UDAY KIRAN
REGNO.: 18MIS0050
FACULTY NAME: ARUNA.K
SLOT: L47+L48
EXPERIMENT – 5A
Z-transforms and their applications for solving
Difference equations
QUESTION 1:
Solve yn+2 −4yn+1 + 3yn = n(2^n), n ≥ 0 y0 = 0, y1 = 0
using Z-transform. Plot the solution
AIM:
To find the solution of the difference equation
using the initial conditions given and Z-transform
MATLAB CODE:
clear all
clc
syms n z y(n) Y
A=input('Enter y(n+2),y(n+1),y(n) coeff in vector
form');

f=input('Enter the non-homogeneous part f(x): ');
cond=input('Enter the initial conditions in form
[y(0),y(1)]: ')
a=A(1);b=A(2);c=A(3);
eqn=ztrans(a*y(n+2)+b*y(n+1)+c*y(n)-f)
y0=cond(1);dy0=cond(2);
eqn=subs(eqn,
{str2sym
('ztrans(y(n),n,z)'),str2sym('y(0)'),str2sym('y(1)')}
,{Y,y0,dy0});
Y=solve(eqn,Y);
y=simplify(iztrans(Y,z,n))
m=0:10;
disp('The solution of the differential equation : ')
disp(y);
y=subs(y,n,m)
stem(y)
INPUT:
Enter y(n+2),y(n+1),y(n) coeff in vector form
[1 -4 3]
Enter the non-homogeneous part f(x):
2*(2^n)
Enter the initial conditions in form [y(0),y(1)]:
[0 0]
OUTPUT:
The solution of the differential equation :
3^n - 2*2^n + 1
y =
[ 0, 0, 2, 12, 50, 180, 602, 1932, 6050, 18660,
57002]

EXPERIMENT – 5B
Solution of homogeneous linear difference
equations
QUESTION 2:
Solve 2yn+2−7yn+1 +3yn = 0 subject to the given
conditions y0 = 1, y1 = 1.Plot the solution.
AIM:
To solve the given difference equation.
MATLAB CODE:
clc
clear all
syms c1 c2 n m
coeff=input('Enter y(n+2),y(n+1),y(n) coeff in vector
form');
n0=input('Enter initial values n0 and n1');
inic=input('Enter the initial conditions in form
[y(n0),y(n1)]: ');
m=roots([coeff(1) coeff(2) coeff(3)])
%or AE=coeff(1)*m^2+coeff(2)*m+coeff(3);m=solve(AE);
disc=coeff(2)^2-4*coeff(1)*coeff(3);
if disc>0
y1=m(1)^n;%first solution
y2=m(2)^(n);%second solution(independent)
elseif disc==0
y1=m(1)^n;
y2=n*m(1)^n;
else
a=real(m(1));%real part of m
b=abs(imag(m(1)));% imaginary part of m
r=sqrt(a^2+b^2);
theta=atan(abs(b)/abs(a));
y1=r^n*cos(theta*n);
y2=r^n*sin(theta*n);
end
y=c1*y1+c2*y2 %complementary solution

[c1 c2]=solve(subs(y,n,n0(1))-
inic(1),subs(y,n,n0(2))-inic(2))
disp('General solution: ');
yn=simplify(subs(y));
disp(yn);
n1=0:10;
stem(n1,subs(yn,n,n1))
INPUT:
Enter y(n+2),y(n+1),y(n) coeff in vector form
[2 -7 3]
Enter initial values n0 and n1
[0 1]
Enter the initial conditions in form [y(n0),y(n1)]:
[1 1]
OUTPUT:
General solution:
(6^n/5 + 4/5)/2^n