Advance Computer Architecture - Desklib

This article covers topics like binary conversion, universal gates, truth table, and more in Advance Computer Architecture. It includes solved assignments, essays, and dissertations on Desklib. The article also provides a truth table and circuit diagram for a combinational circuit.

Advance Computer Architecture

1 | P a g e
Table of Contents
Answer to question 1.............................................................................................................................1
Answer to question 2.............................................................................................................................3
Answer to question 3.............................................................................................................................5
References.............................................................................................................................................7

2 | P a g e
Answer to question 1
a)0x2ED1 to Binary
This digit is in hexadecimal thus now converting into binary
Zero has no value thus ignoring it
2ED1 is now converted from 8421 code.
2=0010
E=1110
D=1101
1=0001
Thus, combining it we get
0010111011010001
Thus, value of binary digit starts from 1
So, the answer is 10111011010001
b) -29.6610 to Binary
For converting this into binary, the value before decimal point is divided by 2 and the value
after decimal point is multiplied by 2
-29/2
Steps Quotient Reminder Number of times
29/2 14 1 0
14/2 7 0 1
7/2 3 1 2
3/2 1 1 3
1/2 0 1
Thus, -29 into binary is = -11101( Writing from down to up)

3 | P a g e
In case of .66
Steps Multiplied Result Reminder
.66*2 .32 1
.32*2 .64 0
.64 .28 1
.28 .56 0
.56 .12 1
.12 .24 0
.24 .48 0
.48 .96 0
.96 .92 1
.92 .84 1
.84 .68 1
.68 .36 1
.36 .72 0
.72 .44 1
.44 .88 0
.88 .76 1
.76 .52 1
.52 .04 1
.04
Thus, .66 into binary is = 101010001111010111( Writing from up to down)
HENCE, 29.6610 to Binary= -11101. 101010001111010111
c) 1001111001102 to Hexadecimal
Converting binary to hexadecimal can be done by 8421 code

4 | P a g e
=1001 1110 0110
=9 E 6
=9E6
d) 11101110 (8-bit 2’s complement representation) to decimal
2’s complement of 11101110 is=
00010001 (1’s complement)
+ 1
= 00010010 (2’s complement)
Now, converting this into decimal:
(0*2^7) + (*2^6) +(0*2^5) +(1*2^4)+ +(0*2^3)+ +(0*2^2)+ +(1*2^1)+(0*2^0)
=18
e) A computer stores the following using the IEEE754 single precision format.
What value in decimal it is representing for:
1 01111110 11000000000000000000000
Converting it into decimal
=(1*2^31) + (0*2^30) + (1*2^29) + (1*2^28) + (1*2^27) + (1*2^26) + (1*2^25) + (1*2^24)
+ (0*2^23) + (1*2^22) + (1*2^21) + (0*2^20) + (0*2^19) + (0*2^18) + (0*2^17) + (0*2^16)
+ (0*2^15) + (0*2^14) + (0*2^13) + (0*2^12) + (0*2^11) + 0*2^10) + (0*2^9) + (0*2^8) +
(0*2^7) + (0*2^6) + (0*2^5) +(0*2^4) + (0*2^3) + (0*2^2) + (0*2^1) + (0*2^0)
=3210739712
Answer to question 2
a) Name two universal gates. Use any one of them to design an inverter
The two universal gates that could be used are NAND and NOR
Using NAND gate as an invertor

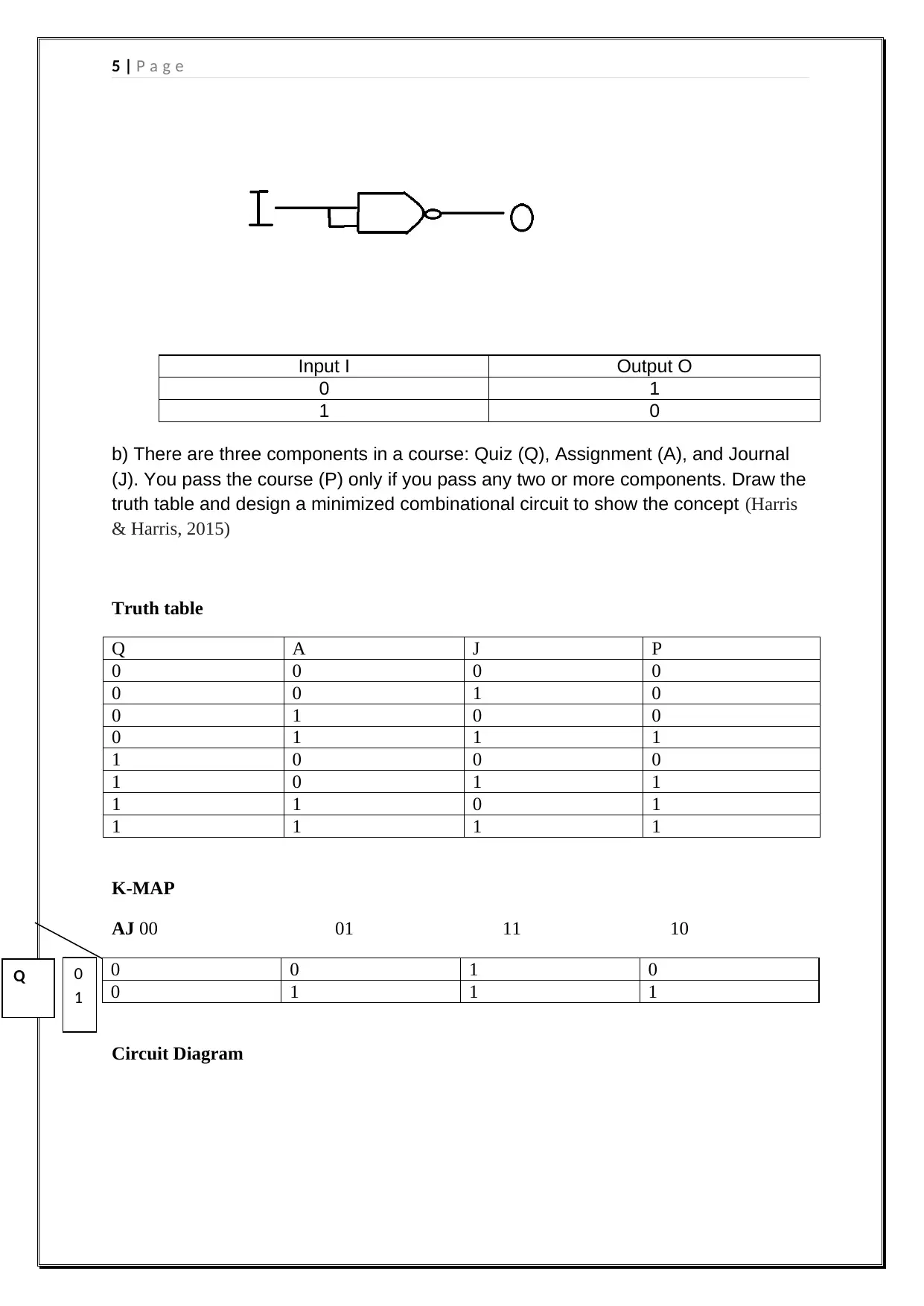
5 | P a g e
Input I Output O
0 1
1 0
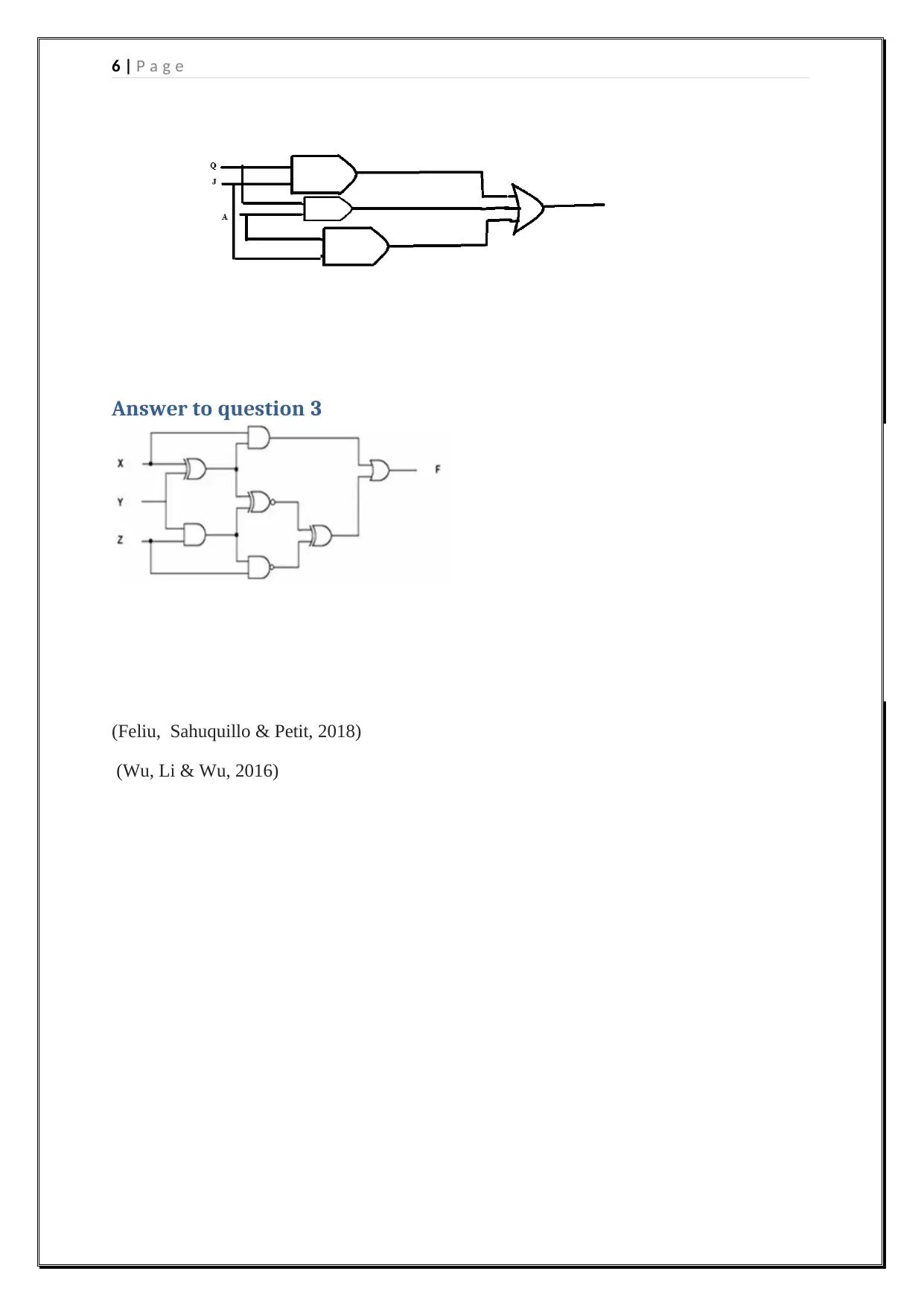
b) There are three components in a course: Quiz (Q), Assignment (A), and Journal
(J). You pass the course (P) only if you pass any two or more components. Draw the
truth table and design a minimized combinational circuit to show the concept (Harris
& Harris, 2015)
Truth table
Q A J P
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 1
K-MAP
AJ 00 01 11 10
0 0 1 0
0 1 1 1
Circuit Diagram
0
1
Q

6 | P a g e
Answer to question 3
(Feliu, Sahuquillo & Petit, 2018)
(Wu, Li & Wu, 2016)

7 | P a g e

8 | P a g e
References
Feliu, J., Sahuquillo, J., & Petit, S. (2018). Designing lab sessions focusing on real
processors for computer architecture courses: A practical perspective. Journal of
Parallel and Distributed Computing, 118, 128-139.
Harris, S., & Harris, D. (2015). Digital design and computer architecture: arm edition.
Morgan Kaufmann.
Wu, J., Li, L., & Wu. (2016). Advanced Computer Architecture. Springer Singapore.