Math 265: Application of Differentiation, Integrals, Application of Integration Solution 2022

Math 265: Application of Differentiation, Integrals, Application of Integration
Unit 5-7: Application of Differentiation, Integrals, Application of Integrations
Solution.
1. why lim
x→ π
6
tan ( 3 x ), does not exist:
lim
x→− π
6
tan ( 3 x ) =lim
h→ 0
tan 3 ( −π
6 +h ) ¿ lim
h→ 0
tan ( −π
2 + 3 h )¿ lim
h→ 0
tan (−π
2 )
¿−∞
Thus, the limit does not exist.
2. U ( x ) = u ( x )
x2 −4 Vertical asymptote : x=2Horizontal asymptote: y =2
U ( x )= u ( x )
x2 −4 = u ( x )
( x−2 ) ( x +2 )
For a Vertical asymptote: x=2, then denominator is x-2=0, thus u(x)
should contain x+2 to cancel out.
For the horizontal asymptote y =2, then the lim
x→ ∞
U ( x )=2
lim
x→ ∞
U ( x ) =
lim
x → ∞
f ( u ( x ) )
x−2 =2 ∴ f ( u ( x ) ) =2 x u ( x ) =2 x ( x +2 )u ( x )=2 x2 +4 x
3. If f(x) is an odd function, then f ( −x ) =−f ( x )
a) F ( x )=x sec ( f ( x ) ) sec (−f ( x ) )=sec ( f ( x ) ) ⟹ sec ( f ( x ) ) is EVEN f ( x )=x is anODD
∴ F (−x )=−x [ sec ( f ( x ) ) ]=−F ( x )
Thus, the function is ODD
b) G ( x )=f (−x ) sin ( x3 ) f (−x ) =−f ( x ) ODDsin ( x3 ) isODD
∴ G ( −x ) =−f ( x ) [ −sin ( x3 ) ] =G( x )

Math 265: Application of Differentiation, Integrals, Application of Integration
Thus, the function is EVEN
4. If f ( x ) = √ cos ( x ) −x
a) The critical values can be calculated in the interval [ – π
2 , 0 ]
d
dx ( f ( x ) ) = d
dx ( √cos ( x )−x )=0 let u=cos ( x )−x¿ df
du . du
dx
df
du = d
dx √ u= 1
2 √ u
du
dx = d
dx ( cos ( x ) −x ) =−sin ( x ) −1 d
dx ( f ( x ) ) = 1
2 √u (−sin ( x )−1 ) = −sin ( x )−1
2 √cos ( x )−x
−sin ( x )−1
2 √ cos ( x )−x =0∴ x=−π
2 critical pont is : (−π
2 , √2 π
2 )
The global (absolute) maxima is (−π
2 , √2 π
2 )
The global (absolute) minima is when x=0, thus ( 0 , 1 )is the absolute
minima.
b) The value where the definite interval, ∫
− π
2
0
√cos ( x )−x dx lies
π
2 (1+ √2 π
2 )=3.53949757
5. If f certifies all the given conditions,

Math 265: Application of Differentiation, Integrals, Application of Integration
Then:
a) The function has an x-intercept in interval (-2, -1) since f(x) is
continuous and f(x) changes from negative to positive
b) The function is not differentiable at x=-2. since f '(x) changes from -
3 to positive abruptly at x=-2
c) The function f has both local maximum and local minimum. The
function f has the local minimum at x=-2 since f ' changes from
negative to positive at x=-2. The local maximum of the function f is
at x=-1 since f ' changes from positive to negative at x=-1
d) Yes, the function f has an inflection point at x=1 since f '' changes
from negative to positive at x=1
e) The function f, does not have vertical asymptote. This is because
the function f is continuous everywhere.
f) The function f, has a horizontal asymptote at y=-1. This is because,
lim
x→ ∞
f ( x ) =−1
6. The area under curves
f ( x )=1+ √ x g ( x ) = 3+x
3
a) The sketch of the area is given in figure below

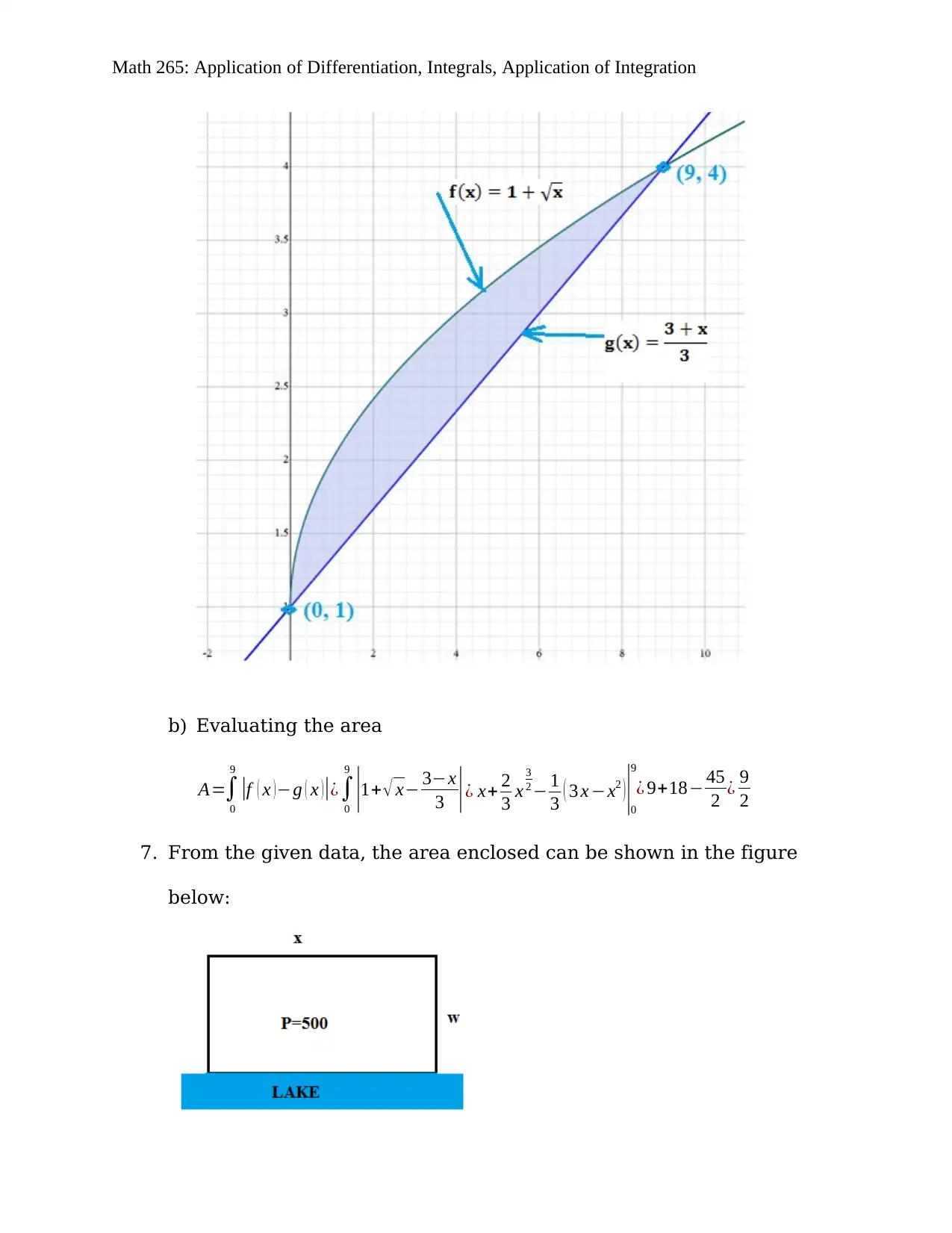
Math 265: Application of Differentiation, Integrals, Application of Integration
b) Evaluating the area
A=∫
0
9
|f ( x ) −g ( x )|¿∫
0
9
|1+ √ x− 3−x
3 |¿ x+ 2
3 x
3
2 − 1
3 ( 3 x −x2 )|0
9
¿ 9+18− 45
2 ¿ 9
2
7. From the given data, the area enclosed can be shown in the figure
below:

Math 265: Application of Differentiation, Integrals, Application of Integration
P ( x , w )=x +2 w=500 x=500−2 w A ( x , w )=xw A ( w )= ( 500−2 w ) w=−2 w2 +500 x
Since the above equation is a parabola that opens downwards, the
vertex is the maximum.
w=−b
2 a = −500
2 ( −2 ) =500
4 =125x=500−2 ( 125 )=250
Thus, the dimension to maximize the area is: x=250 and w=125. The
area will be then 31250
8. The function that satisfies the following
h' ( x )=∫ 2 cos ( 3 x ) sin ( 3 x ) dx¿− cos2 ( 3 x )
3 +Ch' ( 0 )=−cos2 ( 0 )
3 +C= 5
2
−1
3 +C= 5
2 ⟹ C=5
2 + 1
3 = 17
6 h' ( x )=17
6 −cos2 (3 x )
3 h ( x ) =∫ 17
6 − cos2 ( 3 x )
3 dx
¿ 8
3 x− 1
36 sin ( 6 x ) +C2h ( π
2 )= π
3 ⟹ C2= π
3 − ( 8
3 ( π
2 )− 1
36 sin (6 ( π
2 )) )=−π
∴ h ( x ) = 8
3 x− 1
36 sin ( 6 x ) −π
9. Indefinite integral
a) ∫ x √4 x2−5 dx∫ x √4 x2−5 dx= 1
8 ∫ √u du Let u=4 x2−5 ; du
dx =8 x¿ 1
8 (2
3 u
3
2
)+C
¿ 1
8 ( 2
3 ( 4 x2 −5 )
3
2
) +C ¿ ( 4 x2−5 )
3
2
12 +C

Math 265: Application of Differentiation, Integrals, Application of Integration
b) ∫sin2 ( 3 x ) dx∫sin2 ( 3 x ) dx=1
3 ∫ sin2 (u ) du Let u=3 x thus :dx= 1
3 du
¿ 1
3 [ u
2 − cos ( u ) sin ( u )
2 ]+C ¿ x
2 − cos ( 3 x ) sin ( 3 x )
6 ¿ 1
2 x− 1
12 sin ( 6 x ) +C
10. Definite integral
∫
2
5
√ 7 x−2 dx= 1
7 ∫
2
5
√ u du let u=7 x−2 dx= 1
7 du¿ 1
7 ( 2
3 (u
3
2 )|2
5
)= 2
21 ( ( (7 x−2 )
3
2 )|2
5
)
¿ 2
21 ( 33 √33−24 √3 ) ¿ 22 √ 33−16 √ 3
7 ≈ 14.09536647181923
11. The definite integral is correct
12. Using the booth as the reference point, that is at the booth,
distance s0 =0
The car’s position after t seconds when it catches up the track is:
scar =s0 + v0 t + 1
2 a t2
¿ 4 t2
2 =2t2 s0=0 , v0 =0

Math 265: Application of Differentiation, Integrals, Application of Integration
The distance travelled by the truck from the booth;
struck =s0 + v0 t ¿ 2500+50 t scar =struck 2 t2=50t +2500
2 t2−50t−2500=0 Solvingthe quadratc equation
Solving the quadratic equation solves the time taken by the car to
catch up with the truck t= 50± √ 502 +2 ( 4 ) ( 2500 )
2 ( 2 ) ¿ 50 s
The distance from the booth to where the car caught up the truck is:
s=2t2=2 ( 502 )¿ 5000 ft
13. The weight of the chain can be modelled as:
F ( x ) =15 ( 100−x )¿ 1500−15 x
Then, the work done is given as:
W =∫
0
100
F ( x ) dx=∫
0
100
1500−15 x dx¿ 1500 x −15 x2
2 |0
100
¿ 75000 ft ∙lb