Applied Quantitative Methods Assignment 2

This document provides solutions for Applied Quantitative Methods Assignment 2. It includes topics such as frequency distribution, mean, median, mode, standard deviation, correlation coefficient, regression line, correlation of determination, probability, binomial distribution, Poisson distribution, and more.

APPLIED QUANTITATIVE METHODS
ASSIGNMENT 2
Student Name
[Pick the date]

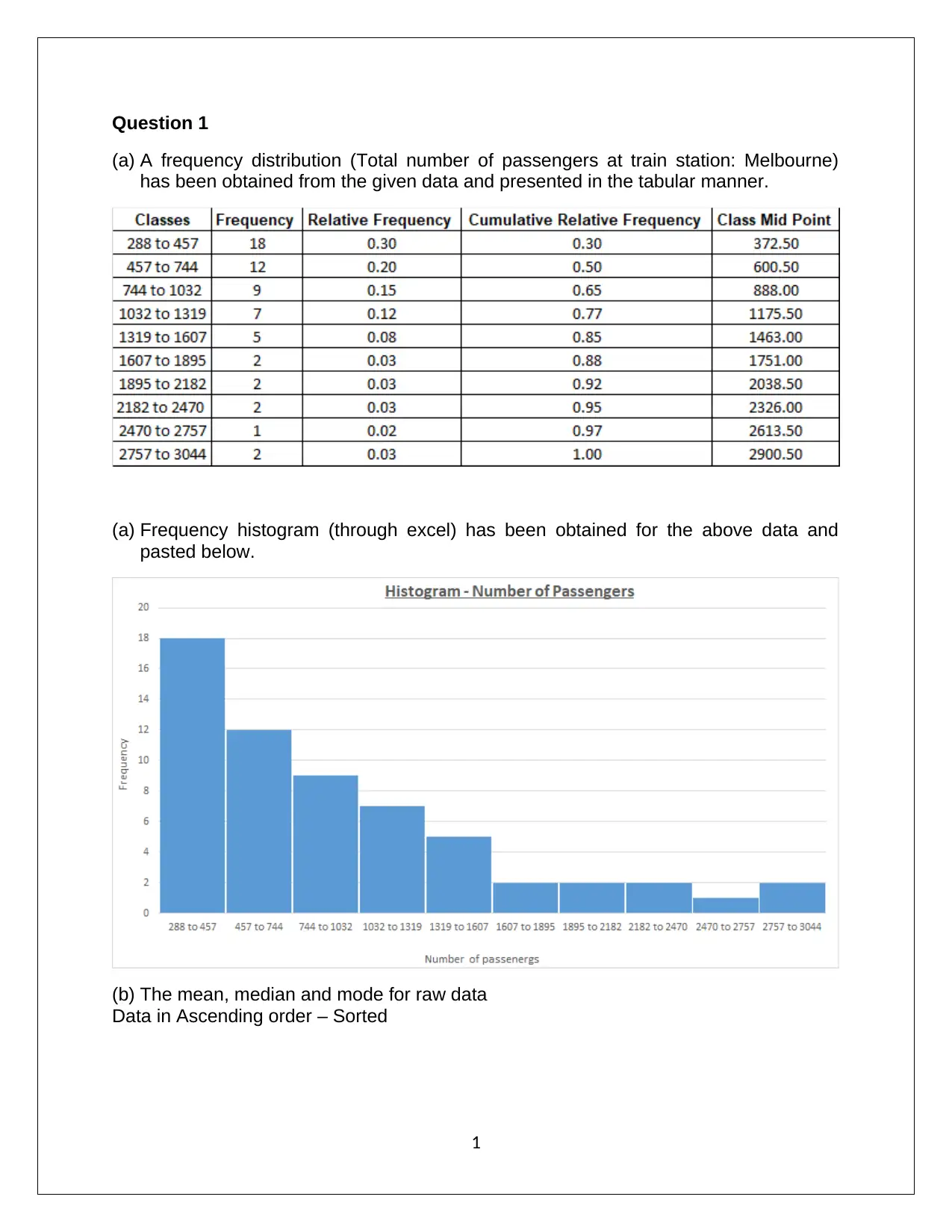
Question 1
(a) A frequency distribution (Total number of passengers at train station: Melbourne)
has been obtained from the given data and presented in the tabular manner.
(a) Frequency histogram (through excel) has been obtained for the above data and
pasted below.
(b) The mean, median and mode for raw data
Data in Ascending order – Sorted
1

2

Mean
Sample size (n) = 60
Total of the sample data points = 58594
Mean of data = 58594/60 = 976.57
Median
Median = ½ {(n/2) value + ((n/2) +1) value} = ½ {(30th value +31st value} = ½
(733+862=797.5
Mode
Maximum occurred number is 401 and thus, it would be the mode of the data.
Question 2
(a) The data that has been given in the question clearly highlights that it corresponds to
only a few of the weeks. The population data would correspond to all the
observations and thereby would have given data for all the 52 weeks present in a
year. However, the data provided only provide information about some selective
weeks and thereby would be declared as sample (Medhi, 2016).
(b) Calculation of standard deviation: weekly attendance
Mean of sample ( = 3392 / 7= 484.57
Standard deviation of sample = ට 1
N−1 σ(x − xത) 2 = ට 1
7−1 × (32909.714) = 74.06
(c) Calculation of Inter Quartile Range: Number of chocolate bars sold
3

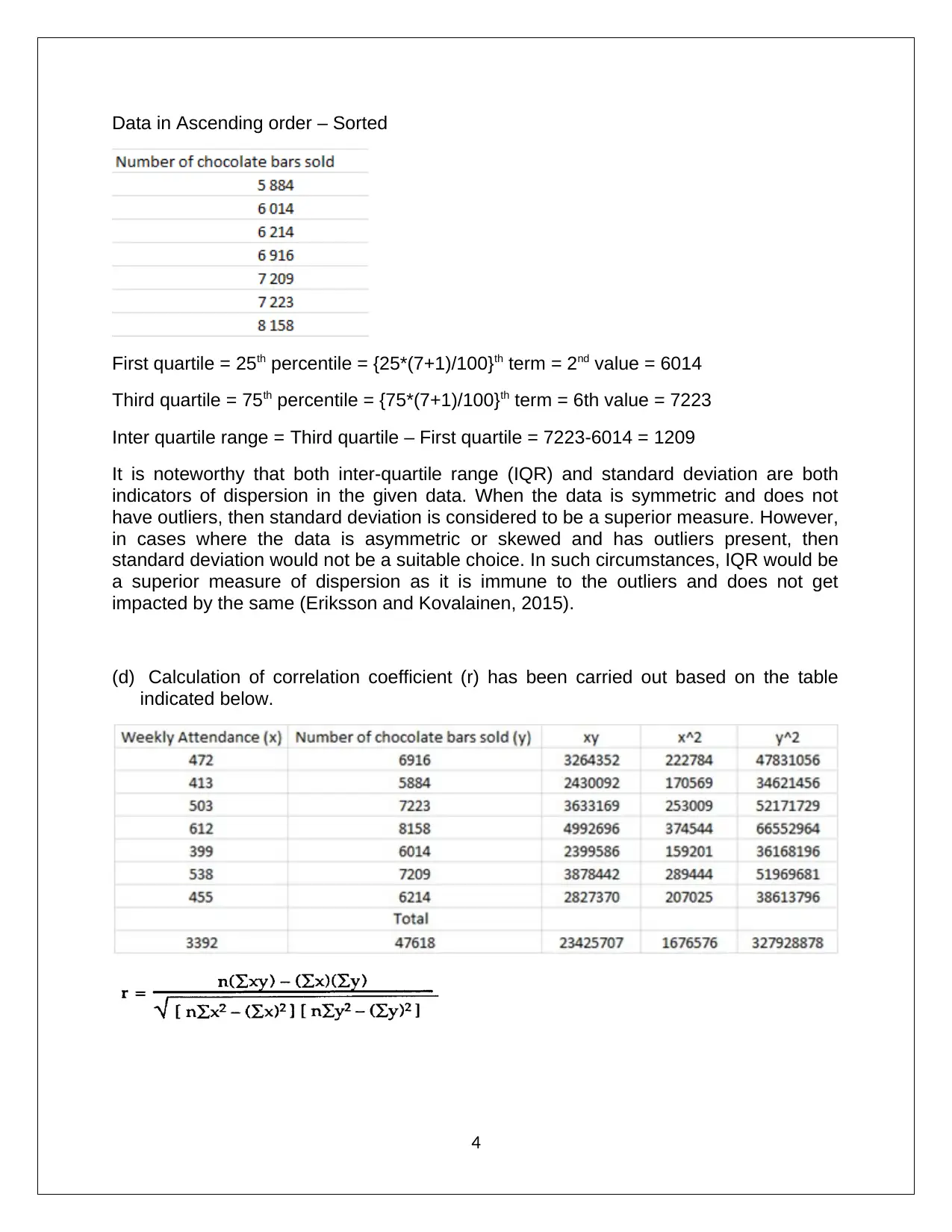
Data in Ascending order – Sorted
First quartile = 25th percentile = {25*(7+1)/100}th term = 2nd value = 6014
Third quartile = 75th percentile = {75*(7+1)/100}th term = 6th value = 7223
Inter quartile range = Third quartile – First quartile = 7223-6014 = 1209
It is noteworthy that both inter-quartile range (IQR) and standard deviation are both
indicators of dispersion in the given data. When the data is symmetric and does not
have outliers, then standard deviation is considered to be a superior measure. However,
in cases where the data is asymmetric or skewed and has outliers present, then
standard deviation would not be a suitable choice. In such circumstances, IQR would be
a superior measure of dispersion as it is immune to the outliers and does not get
impacted by the same (Eriksson and Kovalainen, 2015).
(d) Calculation of correlation coefficient (r) has been carried out based on the table
indicated below.
4

Interpretation: The correlation coefficient has been derived as 0.968. The magnitude of
this correlation coefficient is quite high and almost equal to the maximum value of 1
which would imply that the magnitude of the relationship between weekly attendance
and sale of chocolate bar is quite strong. The value of the coefficient is positive which is
an indication that higher weekly attendance would potentially lead to higher chocolate
bar sales (Hastie, Tibshirani and Friedman,2014).
Question 3
(a) Regression line
Computation:
5

Regression equation
y = 1628.689 +10.67 x
Number of chocolate bars sold = 1628.689 + (10.67* Weekly attendance)
In order to interpret the above regression equation, there are two key aspects that need
to be considered namely the slope coefficient (10.67) and intercept (1628.689). The
intercept coefficient represents the chocolate bars sale that would be expected when
the the weekly attendance is zero. In this case, it would be 1629. Also, the slope
coeffficient highlights the expected change in the dependent variable (chocolate bars
sold) produced by a unit change in the independent variable (i.e. weekly attendance).
Clearly, a change in the weekly attendance by 1 student would result in change in
chocolate bars sale by 10.67 units. The change for the two variables would take place in
the same direction (Taylor and Cihon, 2017).
(b) Correlation of determination (R2)
R square = (
Interpretation: The above value highlights the ability of the given simple regression
model to acocunt for 93.7% of the changes that are visible in the chocolate bar sales on
a weekly basis (Lind, Marchal and Wathen, 2014).
Question 4
Data Given
(a) Probability (Grassroots and Holmes)
6

= (35+92+12)/(35+92+54+12)=0.7202
(b) Probability (Scientific and External)
= 54/(35+92+54+12)=0.2798
(c) Probability (Scientific and Holmes)
= 35/(35+92)=0.2756
(d) Training and Recruitment are independent or not
Event 1 and 2 will be classified as independent when P(A)* P(B) = P (A AND B)
P(A)=Player is external= (54+12)/(35+92+54+12)=0.3412
P (B)=Player is receiving scientific training=(35+54)/(35+92+54+12)=0.4611
P (A). P (P)=0.3412*0.4611=0.1573
P (A AND B) =P (Player is External AND receiving scientific training)=0.2576
P(A)* P(B) = P (A AND B) (not satisfied) and thus, training and Recruitment are not
independent events.
Question 5
(a) Probability (segment A | Product x)
7

Segment Probability
A 0.55
B 0.30
C 0.10
D 0.05
Probability for product X and all the four segments
Segment Probability
P(X|A) 0.20
P(X|B) 0.35
P(X|C) 0.60
P(X|D) 0.90
Required probability
P (A│X)=P(A). P(X|A)/P(X)
= ( (0.55)*(0.2))/ [{(0.55)*(0.2))}+{(0.35)*(0.30)}+{(0.60)*(0.10)}+{(0.90)*(0.05)}]
=0.3537
(b) P (Select product X)
= {ሺ0.55ሻ∗ሺ0.2ሻ)} + {(0.35) ∗(0.30)} + {(0.60) ∗(0.10)} + {ሺ0.90ሻ∗(0.05)} = 0.320
Question 6
8

(a) Probability that 2 or lower than 2 customers will purchase
Binomial distribution
Given information
(b) Probability that in 2 minutes, 9 customers would enter in the shop.
Poisson distribution
9

Question 7
μ =$1.1 million
=$1100000
σ =$385,000
x =$2 million
=$2000000
(a) Probability (Apartment sales > $2 million)
(b) Probability ($1 million < sales< $1.1 million)
10

P (1000000<x<1100000)=P ((1000000-1100000)/385000<(x-μ)/σ< (1100000-
1100000)/385000)=P( -0.26<z<0)
From z table P (z<-0.26)=0.3975
P (z<0)=0.5
P (1000000<x<1100000)=0.5-0.3975=0.1025
Question 8
(a) In order to determine if the underlying data can be considered as normally
distributed or not, consideration needs to be given the central limits theorem. This
theorem states that if the number of observations is adequately large i.e. (greater
than 30), then it would be fair to assume that the underlying sample takes a normal
distribution irrespective of the original distribution being normal (Taylor and Cihon,
2017).
(b) Assistant called 45 investors and out of which 11 investors show willingness to
invest in new fund.
Proportion of agreed investors = 11 /45 = 0.24
Standard error for proportion of sample =√(((1-p)p)/n)= √(0.24(1-0.24)/45)=0.064
Probability (p>30%)=P (z> (0.3-0.24)/0.064)=P(z>0.87)
P (z>0.87)=0.192
Probability (p>30%)=0.192
11

References
Eriksson, P. and Kovalainen, A. (2015) Quantitative methods in business research. 3rd
ed. London: Sage Publications.
Hastie, T., Tibshirani, R. and Friedman, J. (2014) The Elements of Statistical Learning.
4th ed. New York: Springer Publications.
Lind, A.D., Marchal, G.W. and Wathen, A.S. (2012) Statistical Techniques in Business
and Economics. 15th ed. New York : McGraw-Hill/Irwin.
Medhi, J. (2016) Statistical Methods: An Introductory Text. 4th ed. Sydney: New Age
International.
Taylor, K. J. and Cihon, C. (2017) Statistical Techniques for Data Analysis. 2nd ed.
Melbourne: CRC Press.
12