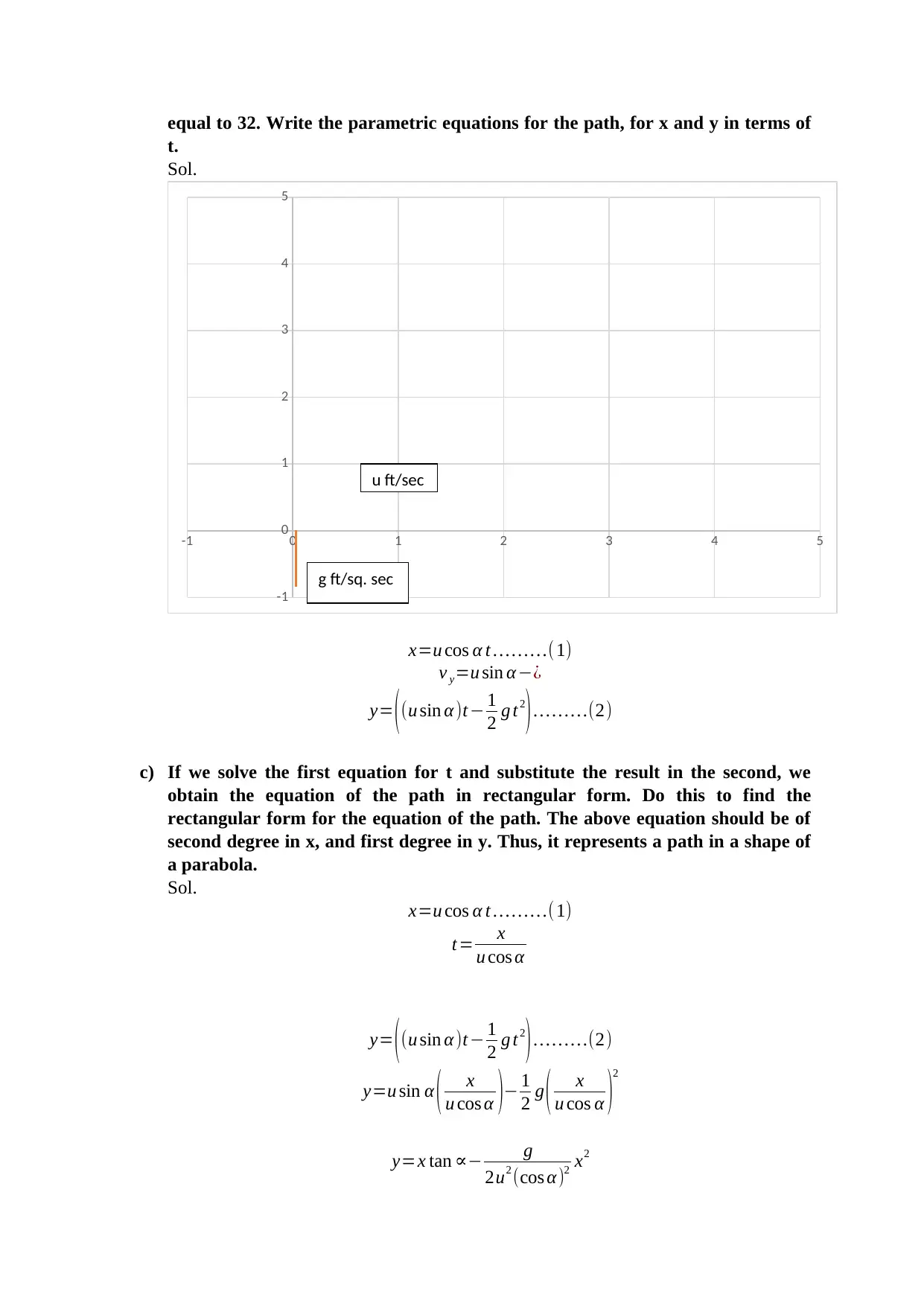
Equations of Projectile Motion

This study material explains the parametric equations and rectangular form of the path of a projectile. It covers the calculations for distance and maximum height of a projectile using these equations. The subject is Mathematics (MTH-1) and the document type is Project - II.

MTH -1
Project - II
<STUDENT NAME>
APRIL 17, 2019

The equations of some curves can be determined more readily by the use of a parameter
than otherwise. In fact, this is one of the principals uses of parametric equations. We
will use parametric equations to help us determine the path of a projectile through the
air.
Suppose that a body is given an initial upward velocity of u feet per second which makes
an angle α with the horizontal. If the resistance of the air is small and can be neglected
without great error, the object will move subject to the force of gravity. This means that
there is no horizontal force to change the speed in the horizontal direction.
If we take the origin to be the point at which the projectile is fired, we see the velocity in
the x-direction (horizontal) is u feet per second. So the distance travelled horizontally at
the end of t seconds is ut feet.
Also, the projectile starts with a vertical component of velocity of v feet per second. This
velocity would cause the projectile to rise upward to a height of h feet in t seconds.
These equations for the path and speed are called parametric equations because they
depend on a parameter t.
a) Draw a picture of the path of the projectile, starting at the origin. Label the x
and y components of the path at some time t>0.
Sol.
-1 0 1 2 3 4 5
-1
0
1
2
3
4
5
b) Our picture doesn’t take into account the pull of gravity, which lessens the
distance travelled. According to a formula of physics, the amount to be
subtracted is from the vertical position is, where g is a constant approximately
X component
y component
u ft/sec

equal to 32. Write the parametric equations for the path, for x and y in terms of
t.
Sol.
-1 0 1 2 3 4 5
-1
0
1
2
3
4
5
x=u cos α t … … …( 1)
v y=u sin α−¿
y= ((u sin α )t− 1
2 g t 2
)… … …(2)
c) If we solve the first equation for t and substitute the result in the second, we
obtain the equation of the path in rectangular form. Do this to find the
rectangular form for the equation of the path. The above equation should be of
second degree in x, and first degree in y. Thus, it represents a path in a shape of
a parabola.
Sol.
x=u cos α t … … …( 1)
t= x
u cos α
y= ((u sin α )t− 1
2 g t 2
)… … …(2)
y=u sin α ( x
u cos α )− 1
2 g ( x
u cos α )
2
y=x tan ∝− g
2u2 (cos α)2 x2
g ft/sq. sec
u ft/sec

d) We will use the parametric equation found in (2) to solve the following problem.
A stone is thrown with a velocity of 160 ft/sec in a direction 45° above the
horizontal. Find how far away the stone strikes the ground and its greatest
height.
a. Substitute α =45° ∧g=32into your equations in (2). Write the resulting
equations below.
Sol.
x=u cos α t … … …( 1)
y= ((u sin α )t− 1
2 g t 2
)… … …(2)
x=u cos 45 ° t
x= ut
√ 2
y= ( ( u sin 45 ° ) t−1
2 32t2
)
y= ((u sin 45° )t−16 t2 )
y= ut
√ 2 −16 t2
b. The stone reaches the ground when y = 0. Substitute this value for y into
the second equation and find t.
Sol.
y= ( ( u sin α ) t − 1
2 g t2
)… … … ( 2 )
0=( (u sin α )t−1
2 g t2
)
( ( u sin α ) t= 1
2 g t2
)
t= 2u sin α
g
c. Use the t-value you found in (b) in the first equation to find x, how far
away the stone strikes the ground.
Sol.
x=u cos α t … … …( 1)
t= 2u sin α
g
x=u cos α 2 u sin α
g
x= u sin 2α
g

d. We know that stone moves along a parabola that opens downwards and
that a parabola is symmetric with respect to its axis. Hence the greatest
height is the value of y when t is half of the flight time. Find t/2 using the
t-value from (b), and substitute it into the second equation of y. the
maximum height.
Sol.
t= 2u sin α
g
t ' = u sin α
g
y= ( ( u sin α ) t − 1
2 g t2
)… … … ( 2 )
y=u sin α u sin α
g −1
2 g u2 (sin α )2
g2
y= u2 (sin α)2
g − u2 (sin α )2
2 g
y= u2 (sin α)2
2 g
5. We will now use the rectangular form of the equation for the path of the projectile,
that you found in (3) to solve the same problem.
a) Substitute α=45° ∧g=32 into your equation from (3). Write the resulting
equation below.
Sol.
y=x tan ∝− g
2u2 ( cos α ) 2 x2
α=45°∧g=32
y=x tan 45° − 32
2(160)2 (cos 45 °)2 x2
y=x − 32∗2
2∗160∗160 x2
y=x − x2
800
b) The stone reaches the ground when y=0. Substitute this value for y into your
equation and find (x,0), the point where the stone strikes the ground.
Sol.
y=x − x2
800
Given y=0
. x= x2
800
x=800
R( 800,0)

c) The vertex is the highest point of the parabola. Use the formula to find the vertex
of parabola, the point of maximum height of the projectile.
Sol.
y= u2 ( sin α ) 2
2 g
y=(160)2 (sin 45°)2
2∗32
y= 160∗160
2∗32∗2
y=200
Maximum height=200 feet