3-Band Audio Amplifier Report 2022

1
3-BAND AUDIO AMPLIFIER
INTRODUCTION.
The objective of this report is to design a 3-band Audio Equalizer. The equalizer has three types
of filters combined. These filters include;
I. Low pass filter whose cut-off frequency is 5kHz.
II. Band pass filter whose corner frequencies are 5kHz and 10kHz.
III. High pass filter whose corner frequency is 5kHz.
The filters are cascaded together with the variable amplifier and summing amplifier as shown in
the schematic below.
Figure 1: Schematic diagram of 3-audio amplifier
The variable gain amplifiers are designed to operate between 0-40dB while the summing
amplifier ought to operate not more than 60dB. The audio speaker is represented by an 8Ω
resistor.
MODELLING OF THE 3-BAND AUDIO AMPLIFIER.
The design was done in stages as below. Implementation of the filter design stage is
accompanied by Multisim simulation. The magnitude frequency plot of the filters’ transfer
functions were done in Matlab software.
Designing of the High Pass Filter ( f >10 kHz filter )

2
First-order High Pass filter was designed using 741 op amp. This type of the filter was preferred
because it is simpler to construct with its underlying mathematical expressions. The filter is as
shown in the figure below [1].
Figure 2: First Order Active High Pass Filter
The transfer function of the First Order High pass filter is expressed as;
H ( ω ) =V o
V i
(1)
Where;
V o −¿Is the output voltage signal.
V i−¿Is the input voltage signal.
Equation (1) can also be expressed using the ratio of output impedance against input impedance
as shown in the equation (2) below.
H ( ω ) =V o
V i
=−Zf
Zi
(2)
Where;
Zf −¿Is the feedback impedance.
Zi −¿Is the input impedance.
The input impedance is series combination of the capacitor Ci and the resistor Ri .
Zi =Ri + 1
jωCi
(3)

3
The output impedance is basically the feedback resistor Rf
Substituting impedances in equation (2);
H ( ω ) = −Rf
Ri + 1
jω Ci
(4)
Rearranging equation (4) results to;
H ( ω ) = − jω Ci Rf
1+ jωCi Ri
(5)
As the frequency tend to infinity, the gain of the filter becomes;
H ( ω ) =lim ¿ ω → ∞ ( − jω Ci Rf
1+ jω Ci Ri ) =−Rf
Ri
(6)
The corner frequency of the First Order High Pass filter is given by;
ωc= 1
Ri Ci
(7)
Making Ri the subject of interest, then;
Ri= 1
ωc Ci
(8)
The cut-off frequency of the Low Pass filter at -3dB is specified as;
f c=10 kHz
Therefore,
ωc=2 π f c=2 π ( 10 , 00 0 Hz ) (9)
ωc=2 0,000 π Rads/sec
Selecting input capacitance as Ci=0. 02 μF , and substituting into equation (8);
Ri= 1
( 2 0,000 π ) ( 0. 02 ×10−6 F ) (10a)
Ri=795.77 Ω
The input resistance is therefore;
Ri=796 Ω (10b)
From equation (6), the D.C gain of the amplifier is given by;

4
H ( ω → ∞ )=−Rf
Ri
(11)
Setting the DC gain of the Low Pass Filter as;
|H ( ω → ∞ )|= Rf
Ri
=4 (12)
Then feedback resistance, Rf , is determined by;
Rf =4 Ri (13a)
Rf =5 ×796 Ω=3,183 Ω (13b)
The feedback resistance is therefore;
Rf =3.2 kΩ (14a)
Substituting the values in equation (5), the transfer function of the first Order High Pass Filter is
given by;
H ( ω ) = − jω ( 0.02 ×3.2 ×10−3 )
1+ jω ( 0.02×796 × 10−6 ) (14b)
Rewriting equation (14b) in complex s-domain;
jω=s
Then the transfer function is;
H ( s )= −s ( 0.02× 3.2×10−3 )
1+s ( 0.02× 796 ×10−6 ) (14c)
The magnitude frequency response of equation (14c) was drawn by help of MATLAB script as
shown below.
%------------------------------------------------------
%------START OF THE CODE-------------------------------
%The script calculates the transfer function of the
% First Order High Pass Filter and plots the
% Magnitude frequency response of the HPF
%-------------------------------------------------------
%------------------------------------------------------
clc;
clear all;
%-----------------------------------------------------
%-----Initializing Transfer Function------------------
s=tf('s');
%-----------------------------------------------------
%------------Transfer function of High Pass Filter----

5
H_hpf = s*(0.02*3.2*10^(-3))/(1+s*(0.02*796*10^(-6)))
%-----------------------------------------------------
%------Plotting Magnitude Frequency Response----------
%----------------------------------------------------
bode(H_hpf)
grid on
title('Magnitude Frequency Response')
xlabel('Frequency')
ylabel('Gain in dB')
%---------------------------------------------------
%---------END OF THE CODE---------------------------
Simplified transfer function of the first Order High Pass filter as computed in Matlab is;
H ( s )= ( 6.4 × 10−5 ) s
( 1.592× 10−5 ) s+1 (14d)
Or H ( jω ) = jω ( 6.4 × 10−5 )
jω ( 1.592 ×10−5 ) +1 (14e)
The magnitude frequency response of the first Order High Pass filter is as shown in the figure
below.
Figure 3: Magnitude Frequency Response of High Pass Filter

6
It is evidenced from the graph that the magnitude frequency plot is giving the characteristics of a
High Pass filter. The filter is only allowing higher frequencies above 5kHz, translating to
approximately 31,000 rads/sec. The frequencies below 5kHz are suppressed.
Simulation of the first Order High Pass Filter ( f >10 kHz filter )
in Multisim
The designed circuit was constructed in Multisim simulation software as shown in the figure
below. The values calculated formed the magnitude basis of the First Order High Pass filter.
Figure 4: High Pass Filter Simulation in Multisim
On simulating the circuit shown above, the following results were obtained.
The input and output signals were confirmed by use of the virtual oscilloscope as shown in the
figure below.

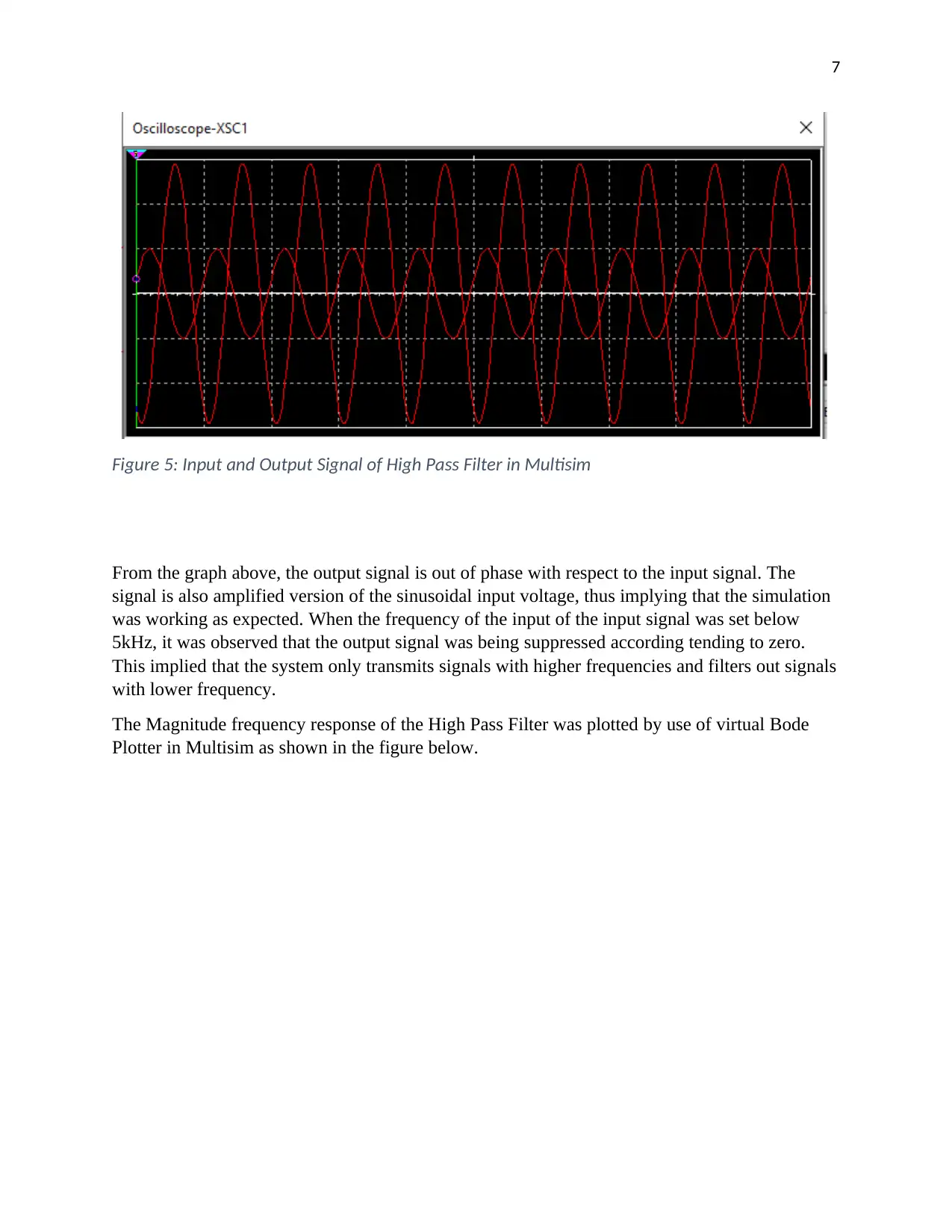
7
Figure 5: Input and Output Signal of High Pass Filter in Multisim
From the graph above, the output signal is out of phase with respect to the input signal. The
signal is also amplified version of the sinusoidal input voltage, thus implying that the simulation
was working as expected. When the frequency of the input of the input signal was set below
5kHz, it was observed that the output signal was being suppressed according tending to zero.
This implied that the system only transmits signals with higher frequencies and filters out signals
with lower frequency.
The Magnitude frequency response of the High Pass Filter was plotted by use of virtual Bode
Plotter in Multisim as shown in the figure below.

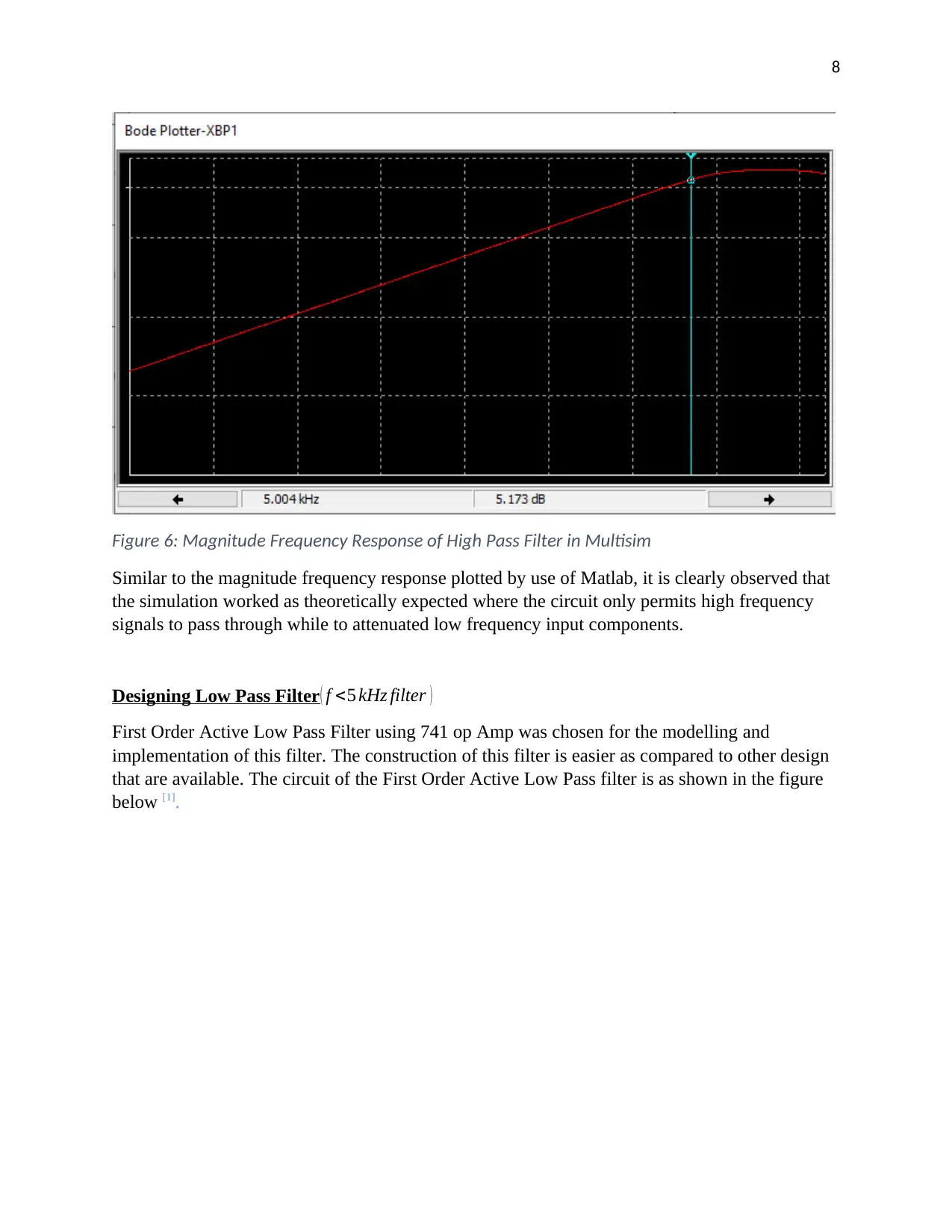
8
Figure 6: Magnitude Frequency Response of High Pass Filter in Multisim
Similar to the magnitude frequency response plotted by use of Matlab, it is clearly observed that
the simulation worked as theoretically expected where the circuit only permits high frequency
signals to pass through while to attenuated low frequency input components.
Designing Low Pass Filter ( f <5 kHz filter )
First Order Active Low Pass Filter using 741 op Amp was chosen for the modelling and
implementation of this filter. The construction of this filter is easier as compared to other design
that are available. The circuit of the First Order Active Low Pass filter is as shown in the figure
below [1].

9
Figure 7: Active First Order Low Pass Filter
The transfer function of the Low pass shown above is given by the ratio of output voltage against
input voltage as shown in the equation below.
H ( ω ) =V o
V i
(15)
Where;
V o −¿Is the output voltage signal.
V i−¿Is the input voltage signal.
Equation (15) can also be expressed using the ratio of output impedance against input impedance
as shown in the equation (16) below.
H ( ω ) =V o
V i
=−Zf
Zi
(16)
Where;
Zf −¿Is the feedback impedance.
Zi −¿Is the input impedance.
The output impedance is parallel combination of the capacitor Cf and the resistor Rf .
Zi =Ri /¿ 1
jωCi
(17)

10
Algebraically, the parallel combination of the impedance components in equation (17) is
expressed as;
Zi =
{ Ri /1
jωCi }
{ Ri + 1
jωCi } (18)
Simplifying equation (118);
Zi = Rf
1+ jωCf Rf
(19)
The input impedance is basically the feedback resistor Ri
Substituting impedances in equation (16), the transfer function of the First Order Low pass filter
is given as;
H ( ω ) =−Rf
Ri { 1
1+ jω Cf Rf } (20)
As the frequency tend to zero, the gain of the filter becomes;
H ( ω ) =lim ¿ ω → 0 ( −Rf
Ri { 1
1+ jωCf Rf })=−Rf
Ri
(21)
The corner frequency of the First Order Low Pass filter is given by;
ωc=ωc=2 π f c= 1
Rf Cf
(22)
But the corner frequency of the Low pass filter is specified as;
f c=5 kHz (23)
Selecting the value of the feedback capacitor as Cf =0.2 μF, then the feedback resistance as from
equation (22) is given by;
Rf = 1
2 π f c Cf
(24)
Substituting the values in equation (24);
Rf = 1
2 π ( 5000 Hz ) ( 0. 02 ×10−6 F ) (25a)
Rf =159 1.54 Ω (25b)
Therefore, the feedback resistance value is found to be;

11
Rf =1.6 kΩ (26)
From equation (21), the DC Low pass filter gain is given by;
H ( ω → 0 ) =−Rf
Ri
(27)
Assuming the DC gain of the Low pass filter is 4, i.e;
|H ( ω → 0 )|= Rf
Ri
=4 (28)
Then, the input resistance Ri is determined by;
Ri= Rf
4 (29a)
Ri= 1600 Ω
4 (29b)
Therefore, the input resistance of the Low Pass filter is;
Ri=400 Ω (30a)
Substituting the values in equation (20), the transfer function of the First Order Low pass filter is
as shown below.
H ( ω ) =−4 { 1
1+ jω ( 1.6 ×0.2 ×10−3 ) } (30b)
Rewriting equation (30b) in complex s-domain;
jω=s
Then the transfer function is;
H ( s )= { −4
1+ s ( 1.6 × 0.2× 10−3 ) } (30c)
The magnitude frequency response of equation (30c) was drawn by help of MATLAB script as
shown below.
%------------------------------------------------------
%------START OF THE CODE-------------------------------
%The script calculates the transfer function of the
% First Order Low Pass Filter and plots the
% Magnitude frequency response of the HPF
%-------------------------------------------------------
%------------------------------------------------------
clc;

12
clear all;
%-----------------------------------------------------
%-----Initializing Transfer Function------------------
s=tf('s');
%-----------------------------------------------------
%--------Transfer function of Low Pass Filter----
H_Lpf = -4/(1+s*(1.6*0.2*10^(-3)))
%-----------------------------------------------------
%------Plotting Magnitude Frequency Response----------
%----------------------------------------------------
bode(H_Lpf)
grid on
title('Magnitude Frequency Response of LPF')
xlabel('Frequency')
ylabel('Gain in dB')
%---------------------------------------------------
%---------END OF THE CODE---------------------------
Simplified transfer function of the first Order High Pass filter as computed in Matlab is;
H ( s )= −4
( 0.00032 ) s+ 1 (30d)
Or H ( jω ) = −4
Jω ( 0.00032 ) + 1 (30e)
The magnitude frequency response of the first Order High Pass filter is as shown in the figure
below.

13
Figure 8: Magnitude Frequency Response of Low Pass Filter
As suggested from the graph above, the high frequency above 5kHz, (31000 rad/sec) component
has been attenuated while the low frequency component has been transmitted. This is the
theoretical characteristics of the Low Pass Filter which filters out high frequency components of
the input signal.
Simulation of the first Order Low Pass Filter ( f <5 kHz filter )in Multisim
The first Order Low Pass filter was constructed in the Multisim software using the designed
values as shown in the figure below

14
Figure 9: Circuit of Low Pass Filter in Multisim
The graph below shows the input and output of the Low pass filter within precinct of the filter’s
working range.
Figure 10: Input and Output signal of the Low Pass Filter in Multisim

15
This graph proves that the filter is capable of attenuating the output signal beyond the cut-off
frequency. Similarly, using Bode Plotter, the Magnitude frequency response of the circuit is as
shown below.
Figure 11: Magnitude Frequency Response of Low Pass Filter in Multisim
From the figure above, is evidenced that below 5kHz, the signals fall within the bandwidth of the
Low Pass Filter.
Designing a Band Pass filter ( 5−10 kHz filter )
The Band Pass Filter is formed by the cascade of unity-gain Low pass filter and unity-gain High
pass Filter in series with an inverter as shown in the figure below [1].
Figure 12: Schematic diagram of Band Pass Filter
Using active filter, the circuit is as shown in the figure below.

16
Figure 13: Active Band Pass Filter circuit
This model of the Band Pass filter is easier to understand and implement unlike other models.
The transfer function of the Band Pass filter is the product of First-Order Low pass’ transfer
function by First-Order High pass’ transfer by the gain of the inverting amplifier.
The transfer function of the First-Order Low pass in equation (20) is;
H ( ω ) =−Rf
Ri { 1
1+ jω C1 Rf } (31)
With unity-gain, where ( Rf
Ri
=1 ) , implying ( Rf =Ri=R )
the transfer function in equation (31) becomes;
H ( ω ) =− { 1
1+ jωC1 R } (32)
The transfer function of the First-Order High pass in equation (5) is;
H ( ω ) = − jω C2 Rf
1+ jωC2 Ri
(33)
With unity-gain, where ( ( Rf =Ri=R ) ) , the transfer function in equation (33) becomes;
H ( ω ) = − jω C2 R
1+ jωC2 R (34)

17
The gain of the inverting amplifier is given by;
K=−Rf
Ri
(35)
Multiplying equation (33, 34 and 35), the transfer function of the Band pass filter becomes;
H ( ω ) =− { 1
1+ jωC1 R }{ jω C2 R
1+ jωC2 R }{ Rf
Ri } (36)
From equation (36), the resistive components of the cascaded Low pass filter and High pass filter
are similar. The resistive component is set as;
R=10 kΩ (37)
The upper cut-off and low-cut off frequencies of the Band Pass filter are specified as;
f 2=10 kHz and f 1=5 kHz (38)
The upper corner frequency of the Band Pass filter is set by the low pass section as;
2 π f 2=ω2= 1
R C1
(39)
And therefore, the capacitance value of the Low pass filter section is determined by;
C1= 1
2 π f 2 R (40)
Substituting the values;
C1= 1
( 2 π ×10,000 Hz ) ( 10 × 103 Ω ) =1.59 nF (41)
Therefore; the capacitor for the Low pass filter section is;
C1=1.59 nF (42)
Similarly, the lower corner frequency of the Band Pass filter is set by the high pass section as;
2 π f 1=ω1= 1
R C2
(21)
And therefore, the capacitance value of the Band pass filter section is determined by;
C2= 1
2 π f 1 R (40)
Substituting the values;

18
C2= 1
( 2 π ×5000 Hz ) ( 10× 103 Ω ) =3.18 nF (41)
Therefore; the capacitor for the Band pass filter section is;
C2=3.18 nF
The center frequency of the Band pass filter is given by;
ω0= √ ω1 ω2=2 π √ f 1 f 2 (42)
Substituting the values;
ω0=2 π √ 5000 Hz ×10,000 Hz (43a)
ω0=44428.8 Rads /sec (43b)
Or f 0=7.071 kHz
The bandwidth of the filter is;
B w=ω2−ω1 (44)
Or B w=f 2−f 1
Substituting the values;
Bw=10 kHz−5 kHz (45a)
Bw=5 kHz (45b)
The quality factor is;
Q= ωo
B =7.071 kHz
5 kHz (46a)
Q=1.41 (46b)
The gain of the passband filter is derived by expressing equation (36) in standard form with
respect to the center frequency, ( ω=ωo = √ω1 ω2 )as shown below.
H ( ωo ) =−Rf
Ri
[ j ωo
ω1
( 1+ j ωo
ω1 )( 1+ j ωo
ω2 ) ] (47)
Multiplying both sides by ( ω1 ω2 ), the expression in equation (47) is simplified to;
H ( ωo ) =−Rf
Ri [ jωo ω2
( ω1+ j ωo ) ( ω2+ j ωo ) ] (48)

19
The magnitude of the transfer function in equation (48) is given by;
|H (ωo )|=
|Rf
Ri
j ωo ω2
( ω1+ j ωo ) ( ω2 + j ωo ) | (49)
Simplifying equation (49), the gain of the passband filter is;
|H (ωo )|= Rf
Ri ( ω2
ω1 +ω2 ) (50a)
Or |H ( f o )|= Rf
Ri ( f 2
f 1 + f 2 ) (50b)
On the inverter section of the Band pass filter, by making the ratio of feedback resistance against
input resistance of the inverter as;
Rf
Ri
=10 (51)
And substituting equation (51) into equation (50b), the expression becomes;
|H ( f o )|=10 ( f 2
f 1 + f 2 ) (52)
Replacing the cut-off frequencies in equation (52), the DC gain of the Band pass filter is;
Rf
Ri
=| H ( f o )|=10 ( 10 kHz
5 kHz+ 10 kHz ) =6.67 (53a)
Rf
Ri
=6.67 (53b)
By selecting Ri=10 kΩ, then
Rf =6.67 Ri =6.67 ( 10 kΩ ) (54a)
Rf =66.7 kΩ (54b)
Substituting the values in equation (36), the transfer function of the first Order Band Filter is
given by;
H ( j ω ) =− { 1
1+ jω ( 1.59 ×1 0−5 ) }{ jω ( 3.18 ×1 0−5 )
1+ jω ( 3.18× 66.7 ×1 0−6 ) } {6.67 } (54c)
Rewriting equation (54c) in complex s-domain;
jω=s

20
Then the transfer function is;
H ( s )= { −6.67
1+ s ( 1.59 ×1 0−5 ) } { s (3.18 ×1 0−5 )
1+s ( 3.18× 66.7 ×1 0−6 ) } (54d)
The magnitude frequency response of equation (54d) was drawn by help of MATLAB script as
shown below.
%------------------------------------------------------
%------START OF THE CODE-------------------------------
%The script calculates the transfer function of the
% First Order Band Pass Filter and plots the
% Magnitude frequency response of the BPF
%-------------------------------------------------------
%------------------------------------------------------
clc;
clear all;
%-----------------------------------------------------
%-----Initializing Transfer Function------------------
s = tf('s');
%-----------------------------------------------------
%--------Transfer function of Band Pass Filter----------
%------------Defining into two sections---------------
G1 = -6.67/(1+s*(1.59*10^(-5)));
G2 = s*(3.18*10^(-5))/(1+s*(3.18*66.7*10^(-6)));
%-------------------------------------------------------
%---------Combining the sections------------------------
%------------------------------------------------------
H_Bpf = G1*G2
%-----------------------------------------------------
%------Plotting Magnitude Frequency Response----------
%----------------------------------------------------
bode(H_Bpf)
grid on
title('Magnitude Frequency Response of BPF')
xlabel('Frequency')
ylabel('Gain in dB')
%---------------------------------------------------
%---------END OF THE CODE---------------------------
Simplified transfer function of the first Order Band Pass filter as computed in Matlab is;
H ( s )= − ( 2.121 ×10−4 ) s
( 3.372× 10−9 ) s2 + ( 2.28 ×10−4 ) s+1 (54e)

21
Or H ( jω )=¿ − jω ( 2.121× 10−4 ) s
( 1−3.372 ×10−9 ω2 )+ ( 2.28 ×10−4 ) s (54f)
The magnitude frequency response of the first Order Band Pass filter is as shown in the figure
below.
Figure 14: Magnitude Frequency Response of Band Pass Filter
As seen from the graph above, the circuit is only allowing certain defined range of frequencies to
pass through while attenuating any other frequency. The low cut-off frequency from the graph is
approximately 31000 rads/sec, which translated to approximately 5kHz. On the contrary, the
upper cut-off frequency is about 62000 rads/sec, translating to approximately 10kHz. Between
these frequencies that define the bandwidth, the circuit is working as theoretically expected.
Simulation of the Band Pass Filter ( 5−10 kHz filter )
in Multisim
The Band Pass filter was constructed in Multisim as shown in the figure below.

22
Figure 15: Band Pass Filter circuit modelled in Multisim
The input and output signals are plotted as shown in the figure below. This suggests that the
circuits can also amplifies or attenuated the output signal.
Figure 16: Input and Output Signal of Band Pass filter in Multisim

23
The magnitude frequency response of the band Pass filter was plotted as shown in the figure
below by use of Bode Plotter.
Figure 17: Magnitude Frequency Response of Band Pass filter in Multisim
The response indicated that the circuit only permits defined range of band pass frequencies to be
transmitted and attenuated any other frequency.
Design of the variable gain amplifier ( 0−40 dB )
The inverting amplifier circuit diagram is as shown in the figure below [1].
Figure 18: Inverting amplifier circuit

24
The input signal is connected to the inverting terminal of the op amp while grounding the non-
inverting positive terminal. Applying KCL at node 1, the following expression is obtained.
i1=i2 (55)
Implying that;
vi−v1
R1
= v1−vo
Rf
(56)
For ideal op amp;
v1 =v2=0 (57)
Therefore, equation (56) becomes;
vi
R1
=−vo
Rf
(58)
The gain expression is;
vo
vi
=−Rf
R1
(59)
The gain magnitude in dB is given by;
Av=−20 log ( Rf
R1 ) (60)
The range of the variable gain amplifier ranges between ( 0 ≤ Av ≤ 40 dB ). This implies that
minimum gain of the variable gain amplifier is;
Amin=−10
0
20 =−1 (61)
Similarly, maximum gain of the amplifier is;
Amax =−10
40
20 =−100 (62)
Therefore, the ratio of input resistance against feedback resistance is;
1 ≤ ( Rf
R1 ) ≤ 100 (63)
And Rf =k R1 (64)
Where
1 ≤ k ≤ 100

25
Making (R¿¿ f )¿ variable knob of the amplifier’s gain and assigning input resistance a constant
value of (R¿¿ i=500 Ω) ¿, then the range of input feedback can be obtained using equation (64)
and extreme values of (k).
Rf ( min )=Ri=500Ω (65)
Rf ( max ) =100 Ri=50 kΩ
The variable feedback resistor is as shown in the figure below.
Figure 19: Variable Feedback resistor of the Variable Gain Amplifier
Design of the summing amplifier ( ≪ 60 dB ).
Summing amplifier stage sums combines the outputs of the filters and gives the weighted sum
equivalent. The circuit of the summing amplifier is as shown in the figure below [1].
Figure 20: Circuit diagram of summing amplifier
This summing amplifier type is an inverting amplifier preferred because it can handle several
inputs concurrently. Owing to extremely high impedance of the op amp, the current entering the
op amp is zero. Therefore, at node a, applying KCL, total current is given by;

26
i=i1 +i2+i3 (66)
These currents are found from the following expressions;
currents=
{i1= V 1
R1
i2= V 2
R2
i3= V 3
R3
(67)
Substituting equation (67) into equation (66),
v0=−Rf ( 1
R1
v1 + 1
R2
v2 + 1
R3
v3 ) (68)
The variable gain of the filters before being fed into the speaker should be less than 60dB.
{20 log ( Rf
R1 ) ;20 log ( Rf
R1 ) ;∧20 log ( Rf
R1 ) } ≤60 dB (69)
In general;
2 0 log ( Rf
R1,2,3 )≤ 60 dB (70a)
log ( Rf
R1,2,3 ) ≤3 0 dB (70b)
Or | Rf
R1,2,3 |≤103 =1000 (71)
Therefore, the ratio should be less than 1000. When Rf =100 kΩ .
Then input resistance for the three amplifiers are chosen arbitrary but within the ratio of less than
1000.
Ri=
{ R1 =2 kΩ
R2=5 kΩ
R3 =10 kΩ
(72)

27
Complete designed circuit connection
The circuit of the 3-band audio amplifier designed was connected as shown in the figure below.
Figure 21: Complete designed circuit of 3-audio amplifier
Transfer function of the whole circuit.
i. Low pass filter cascade branch
The transfer function in this branch is the equivalent transfer function of the series combination
model of the 1st order Low Pass Filter, Variable Gain Amplifier and Summing amplifier.
From equation (30c), the transfer function of the Low pass filter is;
H ( s )= { −4
1+ s ( 1.6 × 0.2× 10−3 ) } (73)
The gain of Variable Gain Amplifier is;
k1 = Rf
Ri
= 50 kΩ
500Ω =100 (74)

28
The gain of the summing amplifier is;
k 2= Rf
Ri
= 10 0 kΩ
2 k Ω =5 0 (75)
The equivalent transfer function of the Low Pass Filter Branch is the product of equations
(73,74, and 75).
H ( LPF )= { −4
1+ s ( 1.6 × 0.2× 10−3 ) }( 100 ) ( 5 0 ) (76a)
H ( LPF )= { −20 , 00 0
1+ s ( 1.6 × 0.2× 10−3 ) } (76b)
ii. High Pass Filter cascade branch
The transfer function in this branch is the equivalent transfer function of the series combination
model of the 1st order High Pass Filter, Variable Gain Amplifier and Summing amplifier.
From equation (14c), the transfer function of the Low pass filter is;
H ( s )= −s ( 0.02× 3.2×10−3 )
1+s ( 0.02× 796 ×10−6 ) (77)
The gain of Variable Gain Amplifier is;
k1 = Rf
Ri
= 50 kΩ
500Ω =100 (78)
The gain of the summing amplifier is;
k3 = Rf
Ri
= 100 kΩ
10 kΩ =10 (79)
The equivalent transfer function of the High Pass Filter Branch is the product of equations
(77,78, and 79).
H ( H PF ) =− { s ( 0.02 ×3.2 ×10−3 )
1+ s ( 0.02 ×796 × 10−6 ) }( 100 ) ( 10 ) (80a)
H ( H PF ) =− { s ( 0.02 ×3.2 )
1+ s ( 0.02 ×796 × 10−6 ) } (80b)

29
iii. Band Pass Filter cascade branch
The transfer function in this branch is the equivalent transfer function of the series combination
model of the 1st order Band Pass Filter, Variable Gain Amplifier and Summing amplifier.
From equation (54d), the transfer function of the Low pass filter is;
H ( s )=−6.67 { 1
1+ s ( 1.59 ×1 0−5 ) } { s ( 3.18× 10−5 )
1+s ( 3.18× 66.7 ×1 0−6 ) }
(81)
The gain of Variable Gain Amplifier is;
k1 = Rf
Ri
= 50 kΩ
500Ω =100 (82)
The gain of the summing amplifier is;
k 4= Rf
Ri
=100 kΩ
5 kΩ =20 (83)
The equivalent transfer function of the High Pass Filter Branch is the product of equations
(77,78, and 79).
H ( B PF ) =−6.67 { 1
1+ s ( 1.59 ×1 0−5 ) }{ s ( 3.18 ×1 0−5 )
1+ s ( 3.18 × 66.7× 1 0−6 ) }( 100 ) ( 20 )
(84a)
H ( BPF ) =− { 13340
1+ s ( 1.59 ×1 0−5 ) }{ s ( 3.18 ×1 0−5 )
1+s ( 3.18 × 66.7 ×1 0−6 ) }
(84b)
iv. Combined transfer function of the circuit.
The equivalent transfer function of the circuit is equivalent to the summation of equations (76b,
80b, and 84b).
∑
{ H ( LPF )= { −20,000
1+ s ( 1.6 ×0.2 ×10−3 ) }
H ( HPF )=− { s ( 0.02 ×3.2 )
1+s ( 0.02 ×796 × 10−6 ) }
H ( BPF )=− { 13340
1+s ( 1.59 ×1 0−5 ) }{ s ( 3.18 ×1 0−5 )
1+ s ( 3.18 × 66.7 ×1 0−6 ) }
(85)

30
The computation was performed in MATLAB as shown by the script below.
%------------------------------------------------------
%------START OF THE CODE-------------------------------
%The script calculates the transfer function of the
% of the combined circuit.
%-------------------------------------------------------
%-------------------------------------------------------
clc;
clear all;
%-------------------------------------------------------
%-----Initializing Transfer Function--------------------
s = tf('s');
%--------------------------------------------------------
%----Transfer function of the Low Pass Filter cascade----
%--------------------------------------------------------
H_Lpf = -20000/(1+s*(1.6*0.2*10^(-3)));
%---------------------------------------------------------
%---Transfer function of the High Pass Filter cascade-----
%---------------------------------------------------------
H_Hpf = s*(0.02*3.2)/(1+s*(0.02*796*10^(-6)));
%---------------------------------------------------------
%---------The tranfer function of the Band Pass Filter----
%---------------------------------------------------------
G1 = -13340/(1+s*(1.59*10^(-5)));
G2 = (s*(3.18*10^(-5)))/(1+s*(3.18*66.7*10^(-6)));
%-----Combining G1 and G2 to give Tf of Bpf---------------
H_Bpf = G1*G2;
%---------Combining the sections--------------------------
%------Equivalent transfer function of the system is the--
%--summation of cascaded transfer functions---------------
%---------------------------------------------------------
%------Plotting Magnitude Frequency Response--------------
%---------------------------------------------------------
T_combined = H_Lpf+ H_Hpf+ H_Bpf
%---------------------------------------------------------
%---------END OF THE CODE---------------------------------
The transfer function of the whole system was found to be;
T (s )comb= ( 6.907 × 10−14 ) s4 + ( 1.65 ×10−9 ) s3− ( 2.472 ×10−4 ) s2− ( 5.239 ) s− ( 20,000 )
( 1.718× 10−17 ) s4 + ( 2.294 ×10−12 ) s3− ( 8.506× 10−8 ) s2− ( 5.639 × 10−4 ) s+ ( 1 ) (86)

31
The combined transfer function is a 4-degree transfer function with same number of zeros and
poles.
COST
Number Name Model Quantity Price for
Each
Total
1 Resistors[2] Carbon-
composition
21 0.05 USD 1.05 USD
2 Capacitors[3] Electrolytic 4 0.5 USD 2.00 USD
3 Op Amp[4] 741 9 0.6 USD 5.40 USD
4 Connecting
wires
copper 5meters 1.0 USD 1.00USD
Total= 9.45USD
CONCLUSION.
The design of the 3-band audio equalizer was developed in stages. The mathematical modelling
based on the desired characteristics was done for each section of the component. The
characteristic behavior of each filter type was observed by plotting magnitude frequency
response by use of Matlab software. Furthermore, the analysis of each filter was proven by
simulation that was performed in Multisim. The results of each filter turned out as theoretically
desired. The transfer function of the whole circuit was also performed, factoring in the arbitrary
gains of the variable gain stage and summing amplifier stage. The combined transfer function
has same number of poles and zeros.

32
REFERENCES.
1. Charles Alexander, Mather Sadiku (2017). Fundamenrals of Electric Circuits. Mc Graw Hill
Education pp. 179, 183, 641.
2. Data Sheet General Purpose Chip Resistor, RC0603", Mouser.com, 2013. [Online]. Available:
https://www.mouser.com/catalog/specsheets/RC0603.pdf. [Accessed: 08- Apr- 2020].
3. "Capacitors Datasheets | Mouser Europe", Eu.mouser.com, 2020. [Online]. Available:
https://eu.mouser.com/Passive-Components/Capacitors/Datasheets/_/N-5g7r. [Accessed: 08-
Apr- 2020].
4. "LM741 Operational Amplifier", 2015. [Online]. Available:
http://www.ti.com/lit/ds/symlink/lm741.pdf. [Accessed: 08- Apr- 2020].

33