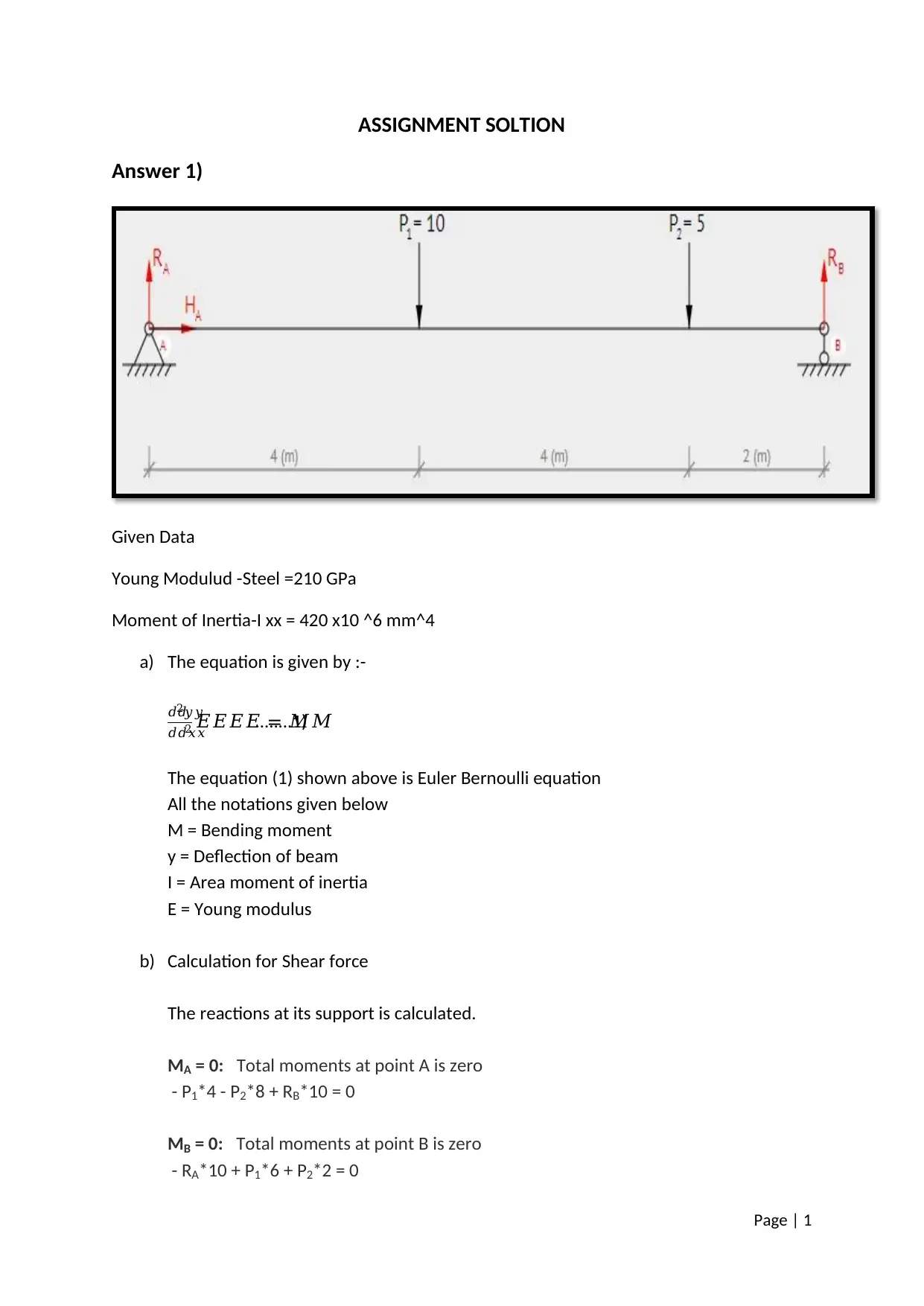
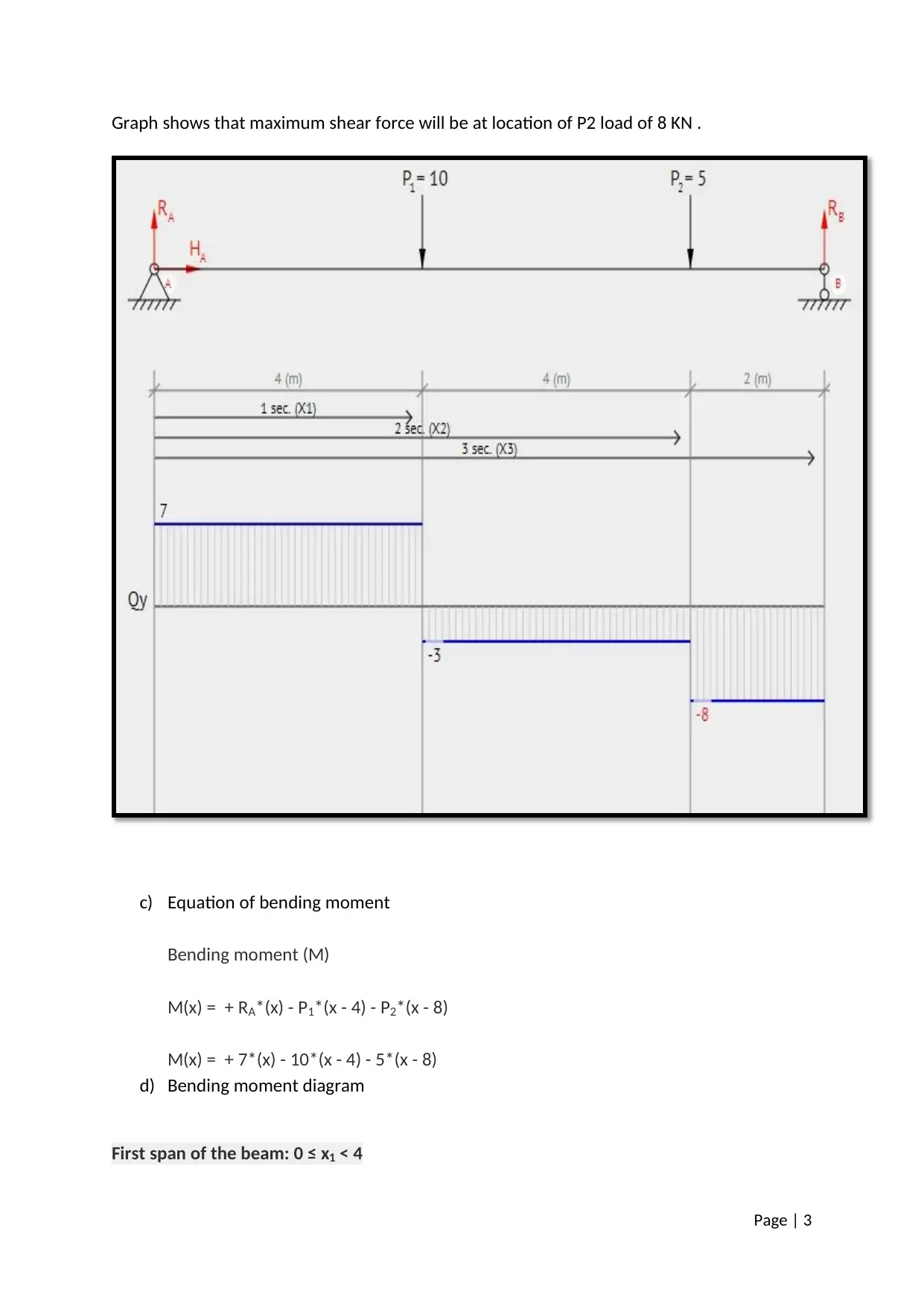
Calculation of Shear Force, Bending Moment, Slope and Deflection of a Beam

This article explains the calculation of Shear Force, Bending Moment, Slope and Deflection of a Beam with solved examples. It also covers the concept of centroid and center of gravity. The calculations are done for a specific beam with given data of Young Modulus and Moment of Inertia. The article also includes graphs and equations for better understanding.

Page | 1
ASSIGNMENT SOLTION
Answer 1)
Given Data
Young Modulud -Steel =210 GPa
Moment of Inertia-I xx = 420 x10 ^6 mm^4
a) The equation is given by :-
𝑑𝑑2𝑦𝑦
𝑑𝑑𝑥𝑥2 𝐸𝐸𝐸𝐸 = 𝑀𝑀........1)
The equation (1) shown above is Euler Bernoulli equation
All the notations given below
M = Bending moment
y = Deflection of beam
I = Area moment of inertia
E = Young modulus
b) Calculation for Shear force
The reactions at its support is calculated.
MA = 0: Total moments at point A is zero
- P1*4 - P2*8 + RB*10 = 0
MB = 0: Total moments at point B is zero
- RA*10 + P1*6 + P2*2 = 0

Page | 2
Solve equations
HA = 0 (kN)
Calculate reaction of roller support at point B
RB = ( P1*4 + P2*8) / 10 = ( 10*4 + 5*8) / 10 = 8.00 (kN)
Calculate reaction of pin support at point A
RA = ( P1*6 + P2*2) / 10 = ( 10*6 + 5*2) / 10 = 7.00 (kN)
First span of the beam: 0 ≤ x1 < 4
Shear force (Q)
Q(x1) = + RA
Q1(0) = + 7 = 7 (kN)
Q1(4) = + 7 = 7 (kN)
Second span of the beam: 4 ≤ x2 < 8
Shear force (Q)
Q(x2) = + RA - P1
Q2(4) = + 7 - 10 = -3 (kN)
Q2(8) = + 7 - 10 = -3 (kN)
Third span of the beam: 8 ≤ x3 < 10
Determine the equations for the shear force (Q)
Q(x3) = + RA - P1 - P2
Q3(8) = + 7 - 10 - 5 = -8 (kN)
Q3(10) = + 7 - 10 - 5 = -8 (kN)

Page | 3
Graph shows that maximum shear force will be at location of P2 load of 8 KN .
c) Equation of bending moment
Bending moment (M)
M(x) = + RA*(x) - P1*(x - 4) - P2*(x - 8)
M(x) = + 7*(x) - 10*(x - 4) - 5*(x - 8)
d) Bending moment diagram
First span of the beam: 0 ≤ x1 < 4

Page | 4
Bending moment (M)
M(x1) = + RA*(x1)
M1(0) = + 7*(0) = 0 (kN*m)
M1(4) = + 7*(4) = 28 (kN*m)
Second span of the beam: 4 ≤ x2 < 8
Bending moment (M)
M(x2) = + RA*(x2) - P1*(x2 - 4)
M2(4) = + 7*(4) - 10*(4 - 4) = 28 (kN*m)
M2(8) = + 7*(8) - 10*(8 - 4) = 16 (kN*m)
Third span of the beam: 8 ≤ x3 < 10
Bending moment (M)
M(x3) = + RA*(x3) - P1*(x3 - 4) - P2*(x3 - 8)
M3(8) = + 7*(8) - 10*(8 - 4) - 5*(8 - 8) = 16 (kN*m)
M3(10) = + 7*(10) - 10*(10 - 4) - 5*(10 - 8) = 0 (kN*m)

Page | 5
Graph shows that the maximum bending moment is at P1 load is equal to 28 KNm.
e) Slope diagram
f) Minimum slope value

Page | 6
The minimum value of slope from the above graph is -0.001 radian .
g) Deflection graph
h) Maximum value of deflection in beam is shown in the graph , The maximum value is -2.902
.The negative sign shows that the deflection is at downward side.
i) The relation between terms
𝑑𝑑2𝑦𝑦
𝑑𝑑𝑥𝑥2 𝐸𝐸𝐸𝐸 = 𝑀𝑀
M(x) = + 7*(x) - 10*(x - 4) - 5*(x - 8)
Solve above equation
M(x) = 80 - 8*(x)
Put the M value in above equation
𝑑𝑑2𝑦𝑦
𝑑𝑑𝑥𝑥2 𝐸𝐸𝐸𝐸 = 80 − 8𝑥𝑥
Differentiate equation two time we get ,
𝒚𝒚 =𝟒𝟒𝟒𝟒∗𝒙𝒙� 𝟐𝟐 −� �
𝟒𝟒
𝟑𝟑
∗𝒙𝒙𝟑𝟑�
𝑬𝑬𝑬𝑬 This above relation is obtain.
2)

Page | 7
a) Graph
b) Area of shaded region
Area of shaded region include 2 parts , one is parabola and other is rectangle.
Equation of area under the curve is given below .
= (5 − 4�
5
4
) −�(𝑥𝑥 − 4)𝑑𝑑𝑥𝑥 +(12 − 5) ∗ 1
= (1�
5
4
) −�(𝑥𝑥 − 4)𝑑𝑑𝑥𝑥 +(7) ∗ 1

Page | 8
= �𝑥𝑥 −
�2 ∗ (𝑥𝑥 − 4)
3
2�
3 �
4
5
+ 7
= (1
3 +7 )𝑚𝑚2
= (22
3 )𝑚𝑚2
𝑨𝑨𝑨𝑨𝑨𝑨𝑨𝑨 𝒐𝒐𝒐𝒐 𝒃𝒃𝒐𝒐𝒃𝒃𝒃𝒃𝒃𝒃𝑨𝑨𝒃𝒃 𝑨𝑨𝑨𝑨𝒓𝒓𝒓𝒓𝒐𝒐𝒃𝒃 =
𝟐𝟐𝟐𝟐
𝟑𝟑𝒎𝒎𝟐𝟐
Position of centroid
Position of centroid in x axis = total moment in x direction /total area
Position of centroid in y axis = total moment in y direction /total area
Consider from graph
𝑥𝑥̅= 𝑥𝑥
𝑦𝑦� =
𝑦𝑦
2
Calculate centroid
𝑥𝑥̅= ∫ 𝑥𝑥̅𝑑𝑑𝑑𝑑
∫ 𝑑𝑑𝑑𝑑
+ 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑑𝑑 𝑐𝑐𝑜𝑜 𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑐𝑟𝑟𝑐𝑐𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑟𝑐𝑐 𝑟𝑟𝑐𝑐𝑐𝑐𝑟𝑟
𝑥𝑥̅= ∫ 𝑥𝑥
5
4 �(𝑥𝑥 − 4)𝑑𝑑𝑥𝑥 + (12 − 5)/2avg
𝑥𝑥̅= ∫ 𝑥𝑥
5
4 �(𝑥𝑥 − 4)𝑑𝑑𝑥𝑥 + (12 − 5)/2avg
= �
�2∗(𝑥𝑥−4)
3
2 ∗� (3𝑥𝑥+8)
15∗0.33 �
4
5
+ (12 − 5)/2avg
= 9.29 + 8.5
2
𝒙𝒙�= 𝟖𝟖. 𝟖𝟖𝟖𝟖𝟖𝟖 𝒎𝒎𝒎𝒎𝑨𝑨 𝒐𝒐𝑨𝑨𝒐𝒐𝒎𝒎 𝒐𝒐𝑨𝑨𝒓𝒓𝒓𝒓𝒓𝒓𝒃𝒃

Page | 9
Similarly calculated for y and obtain
𝑦𝑦� =
∫ 𝑦𝑦 𝑑𝑑𝑑𝑑�
∫ 𝑑𝑑𝑑𝑑
𝑦𝑦� = �
𝑦𝑦
2
5
4
�(𝑥𝑥 − 4)𝑑𝑑𝑥𝑥
𝒚𝒚�= 𝟒𝟒. 𝟒𝟒𝟖𝟖𝟖𝟖 𝒎𝒎𝒎𝒎𝑨𝑨 𝒐𝒐𝑨𝑨𝒐𝒐𝒎𝒎 𝒐𝒐𝑨𝑨𝒓𝒓𝒓𝒓𝒓𝒓𝒃𝒃
c) Position of center of gravity when area revolve around its central axis .
Center of gravity is the sum of all the moment to the total weight of body.
Center of gravity will be similar to point of centroid so center of gravity will be
𝒙𝒙�= 𝟖𝟖. 𝟖𝟖𝟖𝟖𝟖𝟖 𝒎𝒎𝒎𝒎𝑨𝑨 𝒐𝒐𝑨𝑨𝒐𝒐𝒎𝒎 𝒐𝒐𝑨𝑨𝒓𝒓𝒓𝒓𝒓𝒓𝒃𝒃