Bending Stress in Curved Beam - Study on Seismic Resilience and Behaviour of Ancient and Modern Arches

This study focuses on the seismic resilience and behaviour of ancient and modern arches, and the torsional buckling of beams. It evaluates the impact of earthquakes on curved beams and the use of shake table models to test the response of structures. The study also discusses the role of expansion joints in curved beams and the failure modes observed. The subject matter is relevant to engineering and architecture students.

Running head: BENDING STRESS IN CURVED BEAM
BENDING STRESS IN CURVED BEAM

BENDING STRESS IN CURVED BEAM 1
Table of Contents
Introduction......................................................................................................................................2
Task 1: Bending of curved beams...................................................................................................3
1.1 The behaviour of curved beams in past earthquakes.............................................................3
1.2 Shake table model..................................................................................................................6
1.3 Examples of constructions using curved beams..................................................................10
Task 2: Behavior of modern arches vs. the behavior of ancient arches (masonry).......................14
2.1 Failure modes.......................................................................................................................14
2.2 The behaviour of arches in past earthquakes.......................................................................17
2.3 Examples of modern arches and ancient arches...................................................................22
Task 3: Torsional buckling of beams.............................................................................................24
3.1 The reasons behind torsional buckling of beams.................................................................24
3.2 Examples of constructions where the torsional buckling of beams has occurred................25
Conclusion.....................................................................................................................................34
References......................................................................................................................................36

BENDING STRESS IN CURVED BEAM 2
Introduction
A curved beam is generally referred to as a body, the geometric figure of which has been
created by the motion of a plane figure in space. The plane figure is termed as the cross-section
of the curved beam, wherein the center of gravity of the beam consistently follows an axis or a
specific curve. The cross-section of a curved beam can be effectively used to identify the
differences in the curved beams. This study focuses on the curvature of beams concerning
earthquakes. In addition to that, a comparative analysis is mentioned with regards to the varied
behaviour of arches of ancient times with the arches of modern times. For instance, ancient
arches may be illustrated through several medieval architectures, while modern construction
works, such as bridges may be cited as examples of modern arches.
A masonry arch is known to comprise several components, such as a keystone, a
voissour, an impost, an extrados, and an intrados. The other components include a clear span, a
rise, and an abutment. Various types and categories of arches have been explored in this regards
as well. Since beams and may arches are restrained as well as unrestrained, an occurrence
commonly termed as the torsional buckling of beams is found to be prevalent in case the
compression flange becomes free and is found to rotate after being displaced laterally. The
torsional effect has been found to be a result of the combination of both the tensile and the
compressive forces. The reasons for such occurrence have been explored in this study, and the
potential actions for the mitigation of the challenges have been identified in this regards as well.

BENDING STRESS IN CURVED BEAM 3
Task 1: Bending of curved beams
1.1 The behaviour of curved beams in past earthquakes
To evaluate the behaviour of curved beams, it is necessary to consider the design of the
curved beam in question. Considering that the area of cross-sectional of a beam is symmetrical, it
is to be estimated that the impact of the load, which is placed at the plane of symmetry. It may be
mentioned in this context that the axis of symmetry is evident on the plane of curvature.
Furthermore, the determination of the stress which is normal to the cross-section of the beam
may be performed with the aid of the formula depicted in Figure 1.
Figure 1: Formula for determination of stress normal to the cross-section of a beam
(Source: Wang, Lee & Huang, 2016)
The formula represented in Figure 1, can be assessed, where ‘N’ is established to be the
longitudinal force, while ‘F’ is the area of cross-section. Furthermore, ‘M’ is the bending
moment established in the cross-section, with regards to the axis, Z0, which passes through ‘C’
which may be defined as the center of gravity of the cross section (Wang, Lee & Huang, 2016).
On the other hand, ‘y’ is determined to be the distance of the fiber to ‘z,' the neutral axis. The
fiber refers to the one, which is being examined concerning ‘z.' ‘Sz= Fy0’ is defined as the static
moment of the area of cross-section, with regards to ‘z.' ‘P' in this respect can be termed as the
radius of curvature of the fiber. In addition to the aforementioned parameters, the displacement
of the neutral axis ‘Y0’ is estimated to be relative to the center of curvature. It is established that
‘Y0’ is directed towards the center of curvature of the beam to be examined.

BENDING STRESS IN CURVED BEAM 4
Figure 2: Distribution of stress in a cross-section of a curved beam
(Source: Ni, Chen, Teng & Jiang, 2015)
Figure 2 represents the distribution of stress in a curved beam in case of being bent. It is
to be noted that h and d indicate the height and diameter of the beam's cross-section. It may be
stated in this regards that the concave edges of the beam have the maximum values for the
normal stress. Furthermore, the values of normal stress for the beam may vary in the concave
edges, in accordance with hyperbolic law (Ni, Chen, Teng & Jiang, 2015).
To ascertain or study the behaviour of curved beams concerning earthquakes or seismic
movements, the seismic resilience of the beam may be taken into consideration. Under
experimental conditions, the behaviour of curved beams under seismic activities can be
ascertained by studied certain parameters such as the curvature of the beam, ductile cross frames
and the seismic isolation (Di Re, Addessi & Sacco, 2018). In addition to that, the live load,
column rocking as well as the Abutment-soil interaction are to be taken into account for studying
the behaviour of curved beams under seismic activities.
It may be stated in this regards that severe structural damage has been observed in case of
past earthquakes on horizontally curved bridges. The bridges are to be considered as the curved
beams in this regards. Moreover, one of the major issues noted in this respect has been noted to

BENDING STRESS IN CURVED BEAM 5
be the unseating of the deck from the abutment (Di Re, Addessi & Sacco, 2018). This has been
identified as a result of the excessive plane-body motion of the decks, resulting from the seismic
activities. The irregular geometry of the curved beam along with the seismic poundings observed
between the abutments and the decks have been noted to be the prime cause of the failure of the
curved beam structures.
Furthermore, it may be stated in this regards that the maximum seismic response of the curved
beam has been found to be relevant to the angle of input of the designated earthquake (Miyamoto
et al., 2016). The irregularities in the structure of the curved beam or the curved bridge can be
attributed to the interaction between the torsion forces and the moment. The response of the
curved beam structure in response to the input of the one-way earthquake can be determined
through the uniform expression derived from the unfavorable angle of the earthquake. Hence, the
maximum response of the curved beam structure corresponding to the seismic activities of the
earthquake can be determined.

BENDING STRESS IN CURVED BEAM 6
Figure 3: Input angles of earthquake acceleration
(Source: Li & Du, 2015)
Figure 3 represents the various input angles of earthquake acceleration. Figure 3(a)
depicts a single-direction input, while Figure 3(b) depicts orthotropic dual-direction inputs. On
the contrary, Figure 3(c) illustrates Skewed dual-direction inputs relating to the seismic activities
of the earthquakes. The input angles are considered concerning a random direction in a plane.
The implementation of the concept of a curved bridge has been widely prevalent in
several architectural structures. The constructions of railways have a widespread implementation
of the curved beams. However, since the 1970s, multiple devastating earthquakes have been
noted by engineers. The impact of the earthquakes on the curved beams or the girder bridge,
which constitutes an important variation of the curved beams, is regarded as vital for the study
(Hsu & Halim, 2017). For instance, the 1971 earthquake of San Fernando is known to have

BENDING STRESS IN CURVED BEAM 7
caused extensive damage to a multi-span girder bridge. Hence, special attention has been paid to
the seismic responses generated by curved beams or bridges, as a subject for study and
understanding in the field of engineering (Pydah & Sabale, 2017). The Shake table model has
been noted in this regards to developing a better understanding and knowledge concerning the
matter.
1.2 Shake table model
The shake table model has been an extensive aspect of earthquake engineering. The use
and application of the shake table model are observed as a technique implemented to test the
response of certain structures, such as curved beams, or girder bridges to extensive earthquakes.
Furthermore, the study of the seismic performance of rock slopes and soil is also undertaken
through the shake table model. This model is typically used for the evaluation of the performance
of scales slopes, curved beams, and other structural models with the aid of imitating is simulating
earthquakes recorded over some time (Attary et al., 2015). The specimen or the curved beam or
the curved bridge to be shaken is experimented on until it reaches the point of ‘failure.' With the
aid of modern devices and other innovative technologies, it is possible to interpret the dynamic
behaviour of the curved beams exposed to the artificially simulated earthquakes. The degrees of
freedom are generally considered as 6 in this case of the experiment.

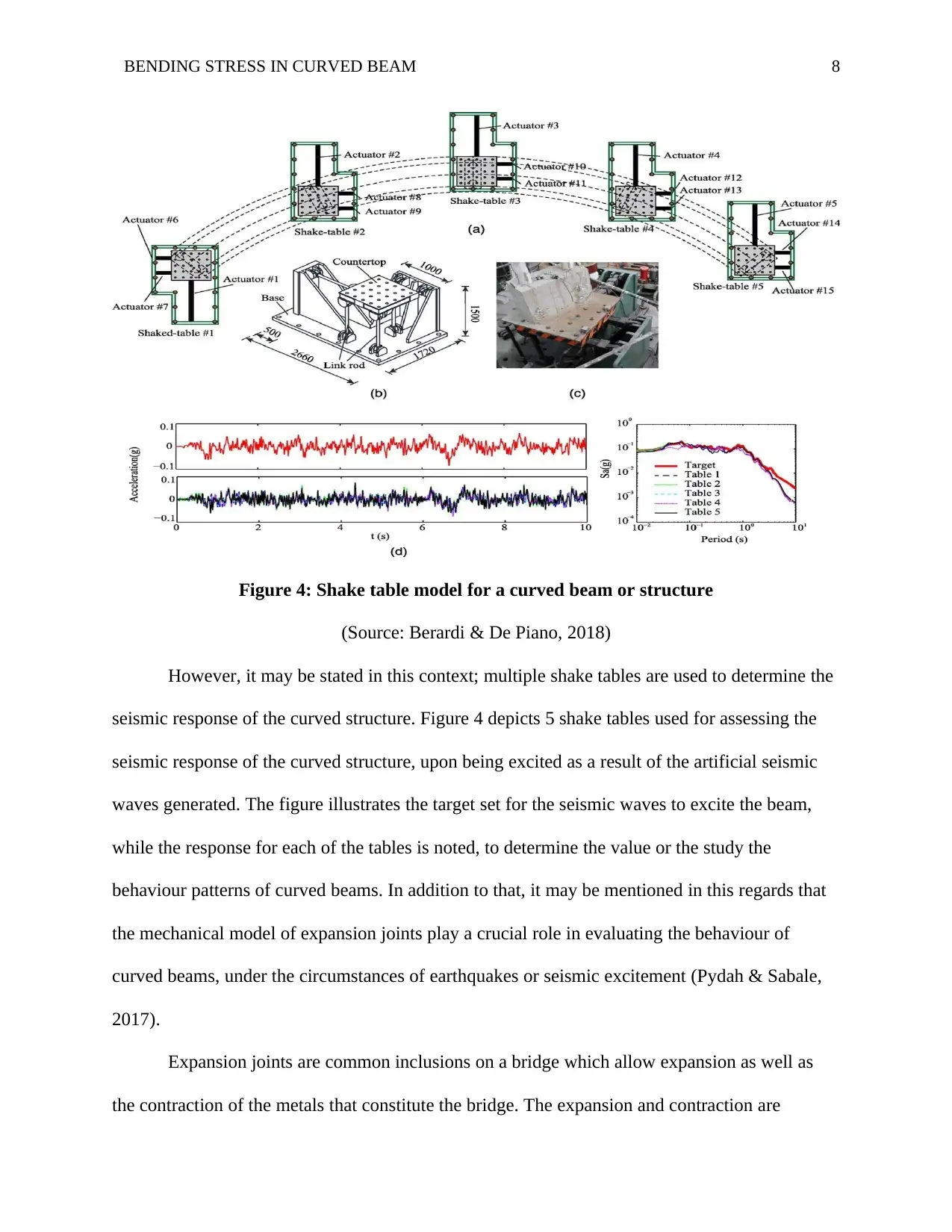
BENDING STRESS IN CURVED BEAM 8
Figure 4: Shake table model for a curved beam or structure
(Source: Berardi & De Piano, 2018)
However, it may be stated in this context; multiple shake tables are used to determine the
seismic response of the curved structure. Figure 4 depicts 5 shake tables used for assessing the
seismic response of the curved structure, upon being excited as a result of the artificial seismic
waves generated. The figure illustrates the target set for the seismic waves to excite the beam,
while the response for each of the tables is noted, to determine the value or the study the
behaviour patterns of curved beams. In addition to that, it may be mentioned in this regards that
the mechanical model of expansion joints play a crucial role in evaluating the behaviour of
curved beams, under the circumstances of earthquakes or seismic excitement (Pydah & Sabale,
2017).
Expansion joints are common inclusions on a bridge which allow expansion as well as
the contraction of the metals that constitute the bridge. The expansion and contraction are

BENDING STRESS IN CURVED BEAM 9
generally consistent with the temperature variations that are a frequent and common occurrence.
Regardless, the absorption of shocks related to the seismic transitions is also regarded as a part of
the application for expansion joints (Berardi & De Piano, 2018). Hence the accommodation of
any machine as well as thermal changes within the system can be achieved through the
implementation of expansion joints in curved beams or curved bridges. The use of reinforced
steel and other steel structures, along with prestressed concrete are used for the development of
the bridge expansion joints to make it be able to withstand seismic activities, which the curved
bridge may be subjected to.
A variety of expansion joints are noted to be in existence. For instance, the expansion
joints are prepared such that it can accommodate certain specific changes being made to the
curved structure. Considering the example of a bridge, one may note that generally, expansion
joints focus on accommodating movement within the range of 30 to 1,200 millimeters (Sun, Cui,
Qin & Hou, 2018). These joints are designed to withstand from small to medium, as well as
large-scale movement. Since this study would eventually discuss the role of masonry in the
resistance towards earthquake on various kinds of arches, it may be suitable to discuss the issues
related to masonry and expansion joints. The curved structures, often made out of masonry may
also display resilience towards seismic activities. The manufacture of rubber expansion joints has
been undertaken to reduce cracks, as well as for shock absorption from the past series of
earthquakes.
It may be mentioned in this regards, that despite major attempts at establishing the
stability of the expansion joints for the curved beams, a failure mode may be evident. The
inability to support or withstand the seismic activities or shocks often results in a failure mode.
The phenomena of collision and yielding have often been responsible for the failure mode

BENDING STRESS IN CURVED BEAM 10
(Berardi & De Piano, 2018). However, the study of these phenomena under seismic shocks can
be used to analyse and evaluate the role or the influence of the expansion joints of the curved
bridges. The study chiefly focuses on assessing the response of the curved beam or the curved
bridge to gather a better understanding of the events. As initially depicted in Figure 3, the multi-
directional inputs of earthquakes have been demonstrated, which aids in the development of an
understanding of the SDOF structure as well. SDOF refers to the single degree of freedom, as
applied previously for the Shake table model, which implements the use of 6 degrees of freedom,
as opposed to one in the SDOF for the study of the multi-directional inputs of earthquakes (Sun,
Cui, Qin & Hou, 2018).
Evaluative studies have been performed upon analysing the deformation of the piers, as
well as the collision and sliding of the expansion joints involved in the curved bridges. It may be
mentioned in this context that among several methods for performing a seismic analysis, the use
of the SRSS combination methods has been focused on by various engineers and scientists.
SRSS, also known as the square root of the sum of the squares is one of the widely preferred
methods for performing the seismic analysis. With the aid of the SRSS method, the use of
response spectrum analysis has been implemented, to analyse the factors involved in the
generation of seismic response (Berardi & De Piano, 2018). The type of pier connection used, as
well as the beam, and the curvature was analysed as being part of the contributing factors.
Furthermore, the use of the complete quadratic combination 3 or the CQC3 method was
implemented to assess the seismic response of the curved structures used in the case study
(Lemos & Campos Costa, 2017).
Regardless, it may be stated in this aspect that the implementation of the Caltrans Seismic
Design Criteria, put forward in 2013, have been found to be the most effective regarding

BENDING STRESS IN CURVED BEAM 11
generating results for the seismic response. The elastic earthquake response can be calculated
from the design above criteria. However, undertaking a study on the better evaluation of a
particular type of curved structure, it was noted that the Caltrans method is more appropriate for
the study of the curved girder bridge (Lemos & Campos Costa, 2017). The reason for the
implementation of the Caltrans method is determined as the suitability of the options regarding
the detailed differences in the construction, while the seismic behaviour is observed in
accordance with the seismic behaviour.
1.3 Examples of constructions using curved beams
The complex geometry involved in the construction, as well as the fabrication of curved
beams, discussed in this study, provides an example of the wide applicability of curved beams.
Furthermore, the study aims at addressing the process of fabrication that implements elastic
deformation for the construction of development using curved beams. Expanding control over
the curvature of the beams as well as the design surface may aid in the establishment of a
network of a quadrilateral mesh, along with a spherical vertex (Sun, Cui, Qin & Hou, 2018). The
advantage of the aforementioned construction can be regarded as the geometric structure which
provides immense support. A symbiosis of the geometry, the fabrication, as well as the load-
bearing behavior of the curved beam structures can be studied in this regards to gathering a better
understanding of the constructions which use curved beams.
A prime example of a construction which implements the use of curved beams can be
cited as the Asymptotic Gridshell which can be designed for courtyards. Figure 5 depicts various
kinds of Gridshell which can be constructed with the aid of curved beams. The figure
demonstrates the principal curvature lines which constitute the major framework for the
gridshell. Furthermore, a traditional gridshell is depicted in the figure, while illustrating the

BENDING STRESS IN CURVED BEAM 12
asymptotic lines present in a gridshell. It may be stated in this regards that gridshells are capable
of bearing massive amounts of load, despite the requirements of very few materials for its
development or construction (Biondini, Camnasio & Titi, 2015). In addition to that, it may be
stated, that the presence of the lamellas aid in the circular development and an elastic assembly
via the weak axis.
Figure 5: Asymmetric Gridshells with curved beams
(Source: Lemos & Campos Costa, 2017)
In addition to that, it may be mentioned in this regards that the network an establishment
as a result of the kinetic behaviour which had been determined formerly. Furthermore, curved
grid structures can be observed to be used in the Eiffel Tower Pavilions which has been designed
by the Moatti Rivière Architects (Biondini, Camnasio & Titi, 2015). Additionally, Frei Otto in
1975 had designed the Multihalle Mannheim which implements a similar use of the curved grid
structures, such as the one mentioned in the Eiffel Tower Pavilion. The right node-angles along
with the circular lamellas are known to be evident on the surface of CMC, which is commonly

BENDING STRESS IN CURVED BEAM 13
known as Constant Mean Curvature (Sarlis et al., 2016). The Multihalle Mannheim is depicted in
Figure 6, while Eiffel Tower pavilions are illustrated in Figure 7.
Figure 6: Multihalle Mannheim constructed with curved beams
(Source: Jiang et al., 2017)

BENDING STRESS IN CURVED BEAM 14
Figure 7: Eiffel Tower Pavilions demonstrating panel types
(Source: Biondini, Camnasio & Titi, 2015)
It may be stated in this regards that the behaviour related to the load-bearing which is
demonstrated by the structures, widely constructed through the implementation of the design of
the curved beams. The study of the load-bearing behaviour may be pointed out as the key to
understanding the seismic response of the structures discussed previously. It may be stated that
since the construction of the curved beam structure does not require many materials for the
provision of support, the resilience that this aforementioned structure may demonstrate with
regards to seismic actions may be considered to be consistent with the load-bearing structures.
Additionally, in case of performing a comparative study between two prime structures which
uses curved beams, namely, a gridshell and a grillage (Sorace & Terenzi, 2016).
The strong axis of both the structures has a bending stiffness, which compels the lamellas
to act as a beam grillage. In addition to that, restraint stresses are noted in the lamellas as a result

BENDING STRESS IN CURVED BEAM 15
of the elastic erection process. However, the bending moment in the weak axis of the curved
elements is noted to increase as a result of the stress created by the compression of the curvatures
present in the curved beams. The combination of the repetitive curvature parameters provides
great potential regarding the load-bearing behaviour and the assembly of the gridshells, which
have been strained as a result of the construction activities and geometric advantages (Franke,
Franke & Harte, 2015).
Task 2: Behavior of modern arches vs. the behavior of ancient arches
(masonry)
2.1 Failure Modes
The modern buildings, bridges, walls of today evolved from the ancient structures. The Roman
people were great builders and architects, and they paved the way for the modern day architects
to make magnificent buildings using definite methods (Li & Zeng, 2016). The Romans were
productive as well as clever and developed span arches, which are smaller to build roofs or
tombs. Gradually the size increased, and they made elaborate bridges as well as amphitheaters.
They created circular arches, parabolic arches, pointed arches and many more. Based on these
models the modern day civil engineers have developed processes to build monuments. While the
ancient people used stones and masonries and developed special concrete of the Roman era, the
modern builders of today use steel and trusses, concrete that is pre-stressed and beams (Li &
Zeng, 2016). The monuments of today have more rigidity and span more than the ancient Roman
civilization.
When something is constructed, there is always the possibility that the construction will face
erosion and damage from natural causes or might be destroyed or damaged for some structural

BENDING STRESS IN CURVED BEAM 16
faults in it (Song, Ming, Wu & Zhu, 2014). To analyze and determine the faults and possible
failures in different structures, the failure modes came into existence in the late 20th century.
Problems, which might arise from malfunctioning constructions, can be easily analyzed by using
a structure, which is high in quality and follows techniques and systems to analyze failure
specifically. They are the initial step for the study of structures in a reliable way. It has some
aspects, which needs to be followed like subsystems, components, and assemblies to identify the
possible modes of failure as well as their effects and causes (Song, Ming, Wu & Zhu, 2014). It
can both be devised as a qualitative tool of measuring flaws and be deemed as quantitative when
the mathematical and statistical model of failure ratio is combined.
The failure modes are considered tools using forward logic or inductive reasoning and can be
used to analyze significant tasks in safety engineering, quality engineering, as well as reliability
engineering (LARSSON, 2015). A mode of failure is considered to be successful when it
identifies imminent failures based solely on the experiences it had with identical processes and
products. The whole concept is based on logic or physics. The failure modes are frequently used
in the industries dealing with manufacturing and development to have the proper idea of the
systems related to the life cycle of a product. In this paper, the failure modes are considered to
understand the modes of failure as well as deformability of materials like concrete (LARSSON,
2015). They are further used in case of masonry to specifically understand the strength of walls
of block masonry, which are significant to formulate the behavioral aspects of assembly.
In the contemporary times, to it is quite hard to understand or determine the results of
experiments done on the interactive nature of materials like blocks of concrete, mortar as well as
the relation between bedding and vertical joints (Costa, Penna, Arêde & Costa, 2015). In this
case, one can use functional analysis to evaluate correct modes of failure. They can also be used

BENDING STRESS IN CURVED BEAM 17
to mitigate risks or to reduce them so that the effect is not so severe. Failure modes are also used
to understand the deformability of masonry walls made of mortar. It has been observed that
failure modes when used to identify faults and flaws in walls made of mortar, they go crushing of
the mortar of bedding as well as a tensile stress and that cut the vertical joint of mortar and the
block as well (Costa, Penna, Arêde & Costa, 2015).
The analysis of reliability can be done using other methods too like the fault tree analysis, which
is a logic played backward or deductive form of analyzing failure and can be used at one time to
find different failures within some item while involving logistics and maintenance (Leonetti et
al. 2018). These modes are used to find an assurance relating to the physical irreversibility and
the damage of the functions, which is not continued through the interface as the failure is part of
ye units of the interface. However, when someone uses the modes of failure, they have to
consider a few things and keep a few things clear (Casapulla & Argiento, 2018). At one point in
time, only one mode of failure can be used to determine flaws in the structure of the masonry.
The inputs, which will be made or analyzed, have to be in the present and needs to have values
that are nominal. All the resources to be consumed have to be present in huge quantities
(Leonetti et al. 2018). They have to make sure that there is the availability of the nominal power.
The failure modes are used frequently to generate results, which can be useful. Therefore, they
have some specific and continuous advantages when implemented to determine the flaws of a
structure or a wall (Greco, Leonetti, Luciano & Trovalusci, 2017). It can provide methods, which
can be documented after a design has been, selected which has a high chance of bringing about
an operation, which is both safe and successful. A method can be documented which will assess
all the possible failure mechanisms, modes as well as the impact of them o the system (Casapulla
& Argiento, 2016). It will result in the formation of modes based on their ranks, which can

BENDING STRESS IN CURVED BEAM 18
determine in the future of how serious they are to be used and what are the chances of it
occurring again. It can be used effectively to determine the effect of the changes, which has been
proposed to design and operate the procedures, which will lead to safety and success (Milani &
Valente, 2015). The failure modes also help to plan early the tests needed to be done in a specific
structure. Through this, one can understand how nonlinearity of masonry will increase
deformation later on with an increase in loading. That will cause the mortar to crack extensively
and will increase progressively the Poisson’s ratio as well as the cracks, which occurred
vertically in the boundary of the joint of blockhead mortar (Fagone, Ranocchiai & Bati, 2015).
2.2 The behaviour of arches in past earthquakes
The discussion of the former tasks presents a case of curved beams. Arches can be
defined as curved beams which are vertical in orientation. Arches have been known to be in
existence for several thousands of years. The ancient architecture forms were primarily
constructed out of masonry, while modern arches can be observed supporting major structure
such as bridges, and so on. The similarity between a curved beam and an arch is quite noticeable.
However, defining an arch, one may state that it may be regarded as a soft compression structure.
On the contrary, it has been noted that curved beams have rigorous engineering activities
involved, along with the calculation derived from the advantageous implementation of the
structural geometry (Baek, Sageman-Furnas, Jawed & Reis, 2018).
It may be mentioned in this regards, that it seems evident that both curved beams, as well
as an arch, have similar structures, they have subtle differences, which may only be identified
through performing a thorough investigation of the same. As discussed in the later stages of this
paper, the major forces which contribute to the construction and stability of an arch are tensile
and compressive forces. The combination of the action of the tensile and compressive forces

BENDING STRESS IN CURVED BEAM 19
establishes and maintains stability of the structure (Lagomarsino, 2015). It may be mentioned in
this context that a curved beam may potentially be an arch. However, the construction of an arch
may not be performed through the implementation of the principles of a curved beam.
Furthermore, it is to be noted that in case of a curved beam, the curve is observed to be incident
on a horizontal plane, while the curve in an arch is noted to be vertical in orientation. Therefore,
it may be clarified that curved beams and arches are different in their structural orientation,
despite the obvious similarities observed.
Figure 8: Types of arches
(Source: Stochino, Cazzani, Giaccu & Turco, 2016)

BENDING STRESS IN CURVED BEAM 20
Regardless of the distinction in their structural orientation, the stability or the resilience
observed in both the structures with regards to earthquakes is a significant subject for
exploration. The forces which come into play in case of an arch are directed towards the ground.
Hence, it may be stated that the arch gradually pushes outward towards the base, which is termed
as thrust. The outward thrust and the height of the arch are noted to be inversely proportional to
one another. The maintenance of the arch action, along with the assurance to prevent the arch
from collapsing, it is crucial to restrain the thrust.
The ancient structures consisting of arches, which are typically made of masonry are
regarded as older forms of architecture. However, modern architecture typically comprises
architecture which uses metals to bend and give certain shapes which are geometrically correct.
Furthermore, the assurance of stability of the structure is provided by both ancient arches as well
as modern arches. Regardless, it is to be mentioned in this context that the development or the
construction of the historical masonry structures were primarily and predominantly designed to
bear gravitation loads (Stochino, Cazzani, Giaccu & Turco, 2016). However, it is to be taken into
account for this study that the provision for preparation and dealing with earthquakes were not
prioritized in those times. Hence, the capability of the masonry arches with regards to
demonstrating resistance towards seismic activities can be regarded as obsolete.
In addition to that, it may be noted that though structures have been structurally stable
and self-supporting, the provision for earthquake combat had not been introduced in the former
arches made out of masonry. Considering the modern day arches, one may state that there are
various considerations to deal and compete with the modern provisions of engineering and
architecture. For instance, the inclusions of the provision of safety with regards to earthquake
have been made a priority in modern arches. The resistance of the compressive stress has been

BENDING STRESS IN CURVED BEAM 21
determined to be the key to the construction of the modern-day arches and relevant structures. In
addition to that, the occurrence of any other forms of stress, namely tensile or torsional stress, is
deliberately reduced (Stochino, Cazzani, Giaccu & Turco, 2016). The reduction in the stress
occurs through the placement of reinforcement fibers or rods.
The stability of the naturally formed aches has not been established. However, certain
examples of modern architecture, which implement the principles of the construction of an arch,
are prime instances of extensive engineering skills of scientists and engineers. One may discuss
the example of ancient arches to better understand the concept implemented in modern
engineering. It may be stated in this aspect that the seismic vulnerability of the ancient arches,
made out of masonry have been noted to be primarily high (Kassotakis, Sarhosis, Forgács &
Bagi, 2017). In addition to that, the properties of the materials used for the construction of the
arches have been found to play a vital role in the high seismic vulnerability of the arches. It has
been found that lower tensile strength, combined with a high specific mass, along with low
ductility as well as moderate shear strength has been observed to be a prime cause of the higher
seismic vulnerability demonstrated by older arches or curved structures.
The dependence of the seismic behaviour of the structure has been found to be primarily
based on the weak connections between the load-bearing walls and the floors, while the
geometry of the structure and the high mass of the masonry wall. These factors have been
observed to have a major influence on the patterns of seismic behaviour of the ancient masonry
arches. The domes, masonry arches as well as vaults have received attention for quite some time
as a result of the factors influencing the seismic resilience of the structures (Sevim, Atamturktur,
Altunişik & Bayraktar, 2016). Modern architectural reforms have identified the flaws, and the

BENDING STRESS IN CURVED BEAM 22
development of the drawbacks with regards to the seismic behaviour can be attributed to the
success and stability of the modern structures.
It has been noted that the steepness in the arch can be the cause of increased stability
among the prevalent modern arch forms. Furthermore, the achievement of the necessary
‘propping action,' which signifies the improved stability of the structure, has been identified with
regards to the seismic behavioural patterns of modern arches. In addition to that, the combining
of the abutments or the bottoms of the arch members are fused may result in the illustration of
better stability of the arches. Hence, it becomes evident from the aforementioned discussion that
the provision for dealing with earthquakes had not been prominent in the early days (Zampieri,
Zanini & Modena, 2015). However, in the modern days, with the progress in the field of science,
engineering, and architecture, the development of concept and ideas and the implementation of
the ideas have been found to be effective in dealing with seismic behaviour of the arches.
2.3 Examples of modern arches and ancient arches
Various examples of ancient arches can be cited through the historical records of
churches and cathedrals. Prime architectural examples include the Rhodes Footbridge which can
be cited as a significant example of the Greek architecture. The Footbridge has been an early
instance of the voussoir arch. In addition to that, the Greek architecture had adapted the
techniques as well as the concept of the construction of an arch (Guo, Yuan, Pi, Bradford &
Chen, 2016). The Romans had realized that an arch does not have to be a semi-circle. The early
identification of this concept led to the rapid and widespread construction of arches throughout
their cities. Furthermore, it is to be taken into account that the segmental arch had initially been
developed by the Romans. The Romans had also implemented the concept into building several

BENDING STRESS IN CURVED BEAM 23
bridges, as well as triumphal arches as military monuments. The Arch of Caracalla is one such
instance of a Roman triumphal arch.
In addition to that, it may be stated that the Europeans had developed similar semicircular
arches leading to the acceptance of Gothic arches or ogives. The Alconétar Bridge may also be
cited as an example of Roman architecture in Spain. The segmental shape of the arches of this
particular bridge in question has been noted to the focus of the specifications of the arches. Ponte
Santa Trinita can be mentioned in this regards as the semicircular arches mentioned before had
been innovated to give the shape of an elliptical structure (Gosden & Malafouris, 2015). Modern
architectures are to be mentioned in this regards. The prime examples of modern arches include
the Woodrow Wilson Memorial Bridge, which is situated between Virginia and Maryland. In
addition to that, the Rainbow Bridge over the river Niagara, which connects the city of New
York to Niagara Falls?
Additionally, the mention of the Hell Gate Bridge over the city of New York is essential
in this aspect. Furthermore, it may be stated that the bridge is considered to be a through arch
bridge. The masonry towers and the steel arch of the Hell Gate Bridge have been left at a gap of
approximately 15 feet. Aesthetic girders were added to the bridge to establish that the robustness
of the structures (Elsayed, Wille, Al-Akhali & Kern, 2017). The girders had been added to the
towers and the upper chord of the arch for additional stability of the structure. Another mention
of modern arches can be cited as the Tyne Bridge, which is a through arch bridge, similar to the
Hell Gate Bridge. However, the Tyne Bridge is located on the river Tyne in Northeast England.
It may be mentioned in this context that the Juscelino Kubitschek Bridge located in
Brazil, can be cited as one of the remarkable works constructed with regards to arches.
Furthermore, the stability of the structure with regards to seismic tolerance has been established.

BENDING STRESS IN CURVED BEAM 24
The bridge has a series of asymmetric arches made of steel, which consistently criss-cross one
another. The diagonal crisscrossing is also considered to be significant reason behind the stability
and self-supporting nature of the bridge (Lacidogna & Accornero, 2018). The seismic resilience
of the bridge has also been noted to be quite high as a result of the geometric advantages that the
structure of the bridge presents. Furthermore, the suspension of the decks with the help of steel
cables and wires constitute a twisted plane, which is an outcome of the interlacing of the steel
cables at each of the sides of the supporting pillars. It is to be taken into account in this regards
that there are four pillars which support the overall structure of the bridge.
Task 3: Torsional buckling of beams
3.1 The reasons behind torsional buckling of beams
Lateral torsional buckling occurs due to unrestrained beam causing displacement in activities. A
beam is referred mostly as unrestrained when it subsequently faces compression caused due to
the external force (Kala, 2015). Mostly, it witnesses flange caused out of free displacement both
laterally and while rotating. For example, when an external load occurs, it causes both lateral
displacements. On the other hand, such movement leads to twisting of a section that is referred to
as lateral torsional buckling. There can be both horizontal and applied vertical load — both may
result in compression and tension causing within the flanges buckling. In such cases, the
compression flange effects and deflects laterally away within the concentrated original position
(Kala, Z. (2015). The tension flange tries to keep the channel straight so that it does not bend.
The lateral movement of the flanges differs based on external and internal force (Kucukler,
Gardner & Macorini, 2015). The lateral bending results in displacement in a certain section that
is unable to restore forces that oppose the movement that occurs generally. It is important to keep

BENDING STRESS IN CURVED BEAM 25
and allow the flange to remain straight. Overall, it is important to restore forces and stops the
risks causing the section from deflecting laterally. It is necessary to foresee both lateral
component and tensile forces that will help in identifying the buckling resistance of the beam
(Ghafoori& Motavalli, 2015). It is important to check the movement of the section and the lateral
forces within the flanges. The most important part is to oversee whether the pressure is
latitudinal or longitudinal.
Figure1-Cause of lateral deflection in the beam
(Source- Trahair, 2017)
The figure above shows, how the twist is created by the torsional stiffness within the section. The
torsional stiffness of the section is pressurized by the flange thickness. It is important to
accommodate thicker flanges that will help in building and bending strength (PB) (Couto, Real,
Lopes & Zhao, 2016). It will help in strengthening the depth of section holding onto the larger
and thinner flanges that might cause lateral deflection within the construction beam.
There are certain factors which influence the behavior of torsional buckling of beams:

BENDING STRESS IN CURVED BEAM 26
1) Location of the applied load- the vertical distance between the point of application of
load and the shear center point of the section which impacts the susceptibility of the
respective section which influences lateral-torsional buckling(Horáček, Melcher, Pešek
and Brodniansky, 2016). When a load is given over the shear center, then there is huge
susceptible buckling than that when the load is applied directly through the shear center.
When a load is below the center, then susceptibility of the section has considerably
reduced the impact of lateral torsional buckling of beams. When there is an application of
load above the shear center then is termed as destabilizing load whereas when loads are
applied through or below the shear center, then it is known as non-destabilizing loads.
The impact of the destabilizing load is taken in the application of lengths; in this scenario,
the lengths are normally lengthier for the destabilizing loads in comparison to the non-
destabilizing loads.
2) The contour of the applied bending moment- the resistance of buckling regarding any
respective section is subjected to a similar distribution of the undeviating bending
moment throughout the whole length is comparably less than resistance gained from
the buckling regarding the same section which was subjected to a distribution with an
altered bending moment. The factors are generally provided within the guidance
provided for the design which allows an understanding of the impacts of all kinds of
distributions of bending moments. The moment factor that is used by the designers is
(MLT) in BS5950- 1:2000.
3) End support conditions- the conditions of end support is reflected at time of the
development of the theory of buckling moments which are similar to the web cleats that
obstruct the web from twisting and lateral deflection(Horáček, Melcher, Pešek and

BENDING STRESS IN CURVED BEAM 27
Brodniansky, 2016). Regarding end conditions, the section endures a lot more resistance
which increases the buckling moment, when the buckling moment is reduced for the end
support then less resistance is offered to the section. BS5950- 1:2000 is considered an
effective length at time of determining section slenderness to understand the impact of
end resistance over lateral torsional buckling.
There are certain degrees of freedom. There are seven degrees of freedom in total in any beam
element in every node. These are considered as translation in x-, y-, and z-direction, and mostly
rotation about x-, y- and z-axis and also wrapping.
Figure 2: Degrees of freedom for a beam element

BENDING STRESS IN CURVED BEAM 28
(Source: Badari and Papp, 2015)
Another most commonly associated situation with lateral torsional buckling is the buckling
conditions. It has been seen that to maintain equilibrium, a certain degree of freedom is needed to
be always restrained at the boundary. When two ordinary beams are considered which are on two
supports then the translations regarding y- and direction regarding z- needs to be always
restrained.
Regarding the translation in x, it is always taken as fixed on one side and free on the other side.
There needs to be the restraint on the x-axis rotation or else the beam would start to rotate on its
axis(Horáček and Melcher, 2017). The support condition can be demonstrated through simple
fork support. The fork has some boundary conditions. The rotation about the x-axis is fixed and
so are the translation in x, y and z, they are fixed as well. However, the rotation about z and y-
axis are free so is Wrapping.
Figure 3: A fork support demonstration.
(Source: Barnet et al., 2017)
An important element of buckling beams is the center of gravity; it is the point in a mass body
where the whole weight of the respective body which can be applied in calculations for
convenience(Horáček and Melcher, 2017). The average of the created gravitational moment from
the body of mass, e.g., the static moment, at this particular point it is zero. The center of gravity

BENDING STRESS IN CURVED BEAM 29
coincides with the centroid only when the material is homogenous. The center of gravity is
generally located in the intersection between the two lines of symmetry in a homogenous I-
section which is double-symmetric.
Figure 4: The I-section demonstration.
(Source: Barnet et al., 2017)
Shear center as discussed above is an important element about the buckling of beams. The shear
center is something, to attain in-plane bending the shear center acts as a point the shear force
needs to act through the line of action. The beams which have cross-sections with double-
symmetry like the I-section, the shear center and the center of gravity coincide(Horáček and
Melcher, 2017). When non-symmetric or single-symmetric section and considered then there are
several instances where the center of gravity and the shear center does not coincide. It can be
demonstrated with a u-section which is loaded with sectional forces and marked out resultants.
The forces within the flanges will result in twisting the section if in the plane web the section is
loaded. Therefore, the shear center can be situated towards the left side of the web where the
equilibrium moment is attained.

BENDING STRESS IN CURVED BEAM 30
Figure 5: The shear center location with the help of a u-section.
(Source: Bedon, Belis and Amadio, 2015)
3.2 Examples of constructions where the torsional buckling of beams has
occurred
In different steel construction there are more than one rows which are parallel and are made of
supported beams which are braced on the top flange. However, the bracing is the relation to the
compression or tension to make sure that the load is transferred toe lateral support that is stiff.
This system is known as ‘a bracing plan system.' The prime utilization of the restraints is to
avoid the deflection of the lateral beams art the bracing points(Vild et al., 2017). The buckling
length of the beams is dependent on the longitudinal distance among the restraints. For this role,
the restraints need a minimum firmness and strength.

BENDING STRESS IN CURVED BEAM 31
Figure 6: Restraints on multiple and single beams
(Source: Kala and Valeš, 2017)
The design of a force in regard to a single brace in any location = qdL, along with this when there
is addition of forces which happen because of the external actions and QD is regarded as the
equivalent stabilizing force and L is regarded as the length of the beam which is restrained(Vild
et al., 2017). At the time of using one or more braces throughout the length of the beam, then it

BENDING STRESS IN CURVED BEAM 32
needs to be designed in such a way that it can resist a minimum force which is no less than
5qdL/8, in addition to the extra additional forces by the actions which are external. Determining
the restraint forces is an iterative procedure, because of the level of bracing system deflection on
which the forces are dependent. The typical bracing systems which are applied in the buildings,
the deflections of these are improbable to surpass L/2000. When this value is considered to be
qDQ, then 2.0% restraint forces in maximum designs force regarding the compression flanges
seems to emerge from an equation of a single restraint beam, where again the additional forces
because of external actions are to be added(Yang et al. 2016). In this scenario, iteration is not
required only if the deflection of the bracing system qDQ is less than L/2000. If L/2000 is
exceeded by DQ, then the restraint forces that are gathered with become unsafe. When all these
conditions are fulfilled, then the beam can be designed with a length of Lcr which is also equal to
the distance among the braced points. It is very important for the lateral support to be capable of
bear the force of bracing transferred to it safely. In case of a splice in a particular beam then the
bracing system needs to be capable resisting the lateral force impacts which are equivalent to the
1% force of the design at the location of splice within the compression flange.
In the scenario of the multiple beams, the bracing needs to be designed for the average of all the
restraint forces for every single beam (Ozbasaran, Aydin and Dogan, 2015). There is universal
regulation, the lateral firmness of the whole system of restraining need not exceed 25 times even
when combined with the stiffness of the lateral beams which will be braced. The typical
restraining system is formed of a truss type bracing in the beams compressional flanges plane.

BENDING STRESS IN CURVED BEAM 33
Figure 7: Multiple beams construction
(Source: Kala and Valeš, 2017)
The stability of more than two lateral beams can be improvised by interconnecting the beams at
certain intervals throughout their lengths via the bracing plan system. The restraint system solely
relies on the connection of a few unstable members which is needed to be ensured that the
instability will lead to the deformation of the system of bracing(Ozbasaran, Aydin and Dogan,
2015). Therefore, just connecting the beams with its end pinned with light-crossed members will
not give any result as the buckling mode of the beams are not affected in the least. Total lateral
restraint regarding the compression flanges is attained at the points which are braced, although
the bracing members need to be bonded to the flanges, they also need to be able to resist the
equivalent stabilizing force dQD. Lateral torsional buckling of the beams' resistance is needed to
be verified among the points which are braced. The resistance forces which are individual
regarding the percentages of the compression forces of the flanges that is maximum are as well
as suitable in this perspective.

BENDING STRESS IN CURVED BEAM 34
Figure 8: Braced pairs of beams
(Source: Jiao, Borchani, Soleimani and McGraw, 2017)
In several instances, it has been observed that there are beams which support the cavity walls,
and their designs are a bit tricky(Ozbasaran and Yilmaz, 2018). When there are two beams which
are adjacent to each other which is normally hot rolled I channels, then it generally leads to
supporting both the leaves on a cavity wall. These beams are needed to be connected at certain
intervals by diaphragms or separators. The separators ensure that among the two beams there is a
space or not. They are capable of carrying transverse forces but are incapable of transferring

BENDING STRESS IN CURVED BEAM 35
vertical forces among the beams. For the loaded beams which are equally loaded, the separators
guarantee that both the beams will buckle in the similar direction, however, there is no evidence
of increased capacity for carrying the load above the average of the beams individually.
The function of the diaphragms is to retain the structure and shape of the cross sections at their
respective locations, and as a result, the beams are provided and supported with torsional
restraint(Naaim, De’nan, Keong and Azar, 2016). The diaphragms are capable of transferring
vertical load among the beams however the beams need to contain enough firmness and strength.
Hence, the resistance of the beams will be known as the braced pair of beams.
Figure 9: diaphragms and separators
(Source: Jiao, Borchani, Soleimani and McGraw, 2017)
In the steel construction,n there are beams where there is restraint with beams comprised of the
tension flange. This is observed mostly in the outer columns and the regions with the hogging

BENDING STRESS IN CURVED BEAM 36
moments regarding the rafters mostly in the portal frames of the single story, here the tensions
restraints are given through side rails(Lopes, Couto, Vila Real and Lopes, 2016). These elements
normally provide complete lateral restraint however no torsional restraint is given to tension
flange — there two types of approaches that are followed to understand the member's stability
among the torsional restraint.
 For the elastic design determining the resistance of member buckling.
 For the plastic design determining the stable length.
In both of the methods, two checks are needed to be done. Firstly, the beam stability about the
flexural torsional mode among the flanges' restraints, secondly, the stability of the beams are
needed to be assessed among the restraints of the tension flanges.
There beams in the construction that supports the timber floors which also has the application of
torsional buckling beams. It is very common to see that a sequence of steel beams was proving
support to the timber floor, it is mostly found in older buildings. In this kind of constructions, it
is seen that under the joists of the timber or completely inside the floor the steel beams are
located(Lopes, Couto, Vila Real and Lopes, 2016). The level at which both the timber joists
provide lateral resistant to steel beams is completely dependent on the connection among these
two elements. When there is a positive connection in-between the timber joists and the steel
beams, then it can be presumed that the steel beams are lateral and restrained by the timber joists.
In this scenario, there are certain recommendations which are provided. The edge beams that are
there need a special reflection as being notched by its own does not provide any restraint. In this
scenario, steel straps are required. The restraint forces which are transmitted to the timber joists
are generally small or less for the normally sized beams which can be resisted with the help of

BENDING STRESS IN CURVED BEAM 37
the diaphragms or by attaching or packing the timber joists ends firmly by the walls of the
masonry(Kucukler, Gardner and Macorini, 2015). When the steel beams are larger than the and
support heavy walls or loads, then a proper position for lateral restraints is needed to be
developed with the help of straps and braces. The firm points on the structure like the walls need
to bear the restraint forces, or it can be transferred to the floors with the help of diaphragm in the
presence of the floorboards and its needed to be made sure that they are attached to the timber
joists.

BENDING STRESS IN CURVED BEAM 38
Figure 10: Timber floors being supported by beams.
(Source: Kucukler, Gardner and Macorini, 2015)
The beams which support concrete slabs also the application of lateral torsional buckling of
beams have been found. When a sequence of beams which are parallel to each other are
supporting a concrete slab, they will either function compositely of non-compositely(Kucukler,
Gardner and Macorini, 2015). It acts compositely simply because of the presence of the shear
connectors. In the case of two precast units which are grouted. When composite beams are used
then there is the total restraint given to the beams with the help of the action of diaphragm inside
the slab and as discussed above it happens through the shear connectors. The composite beams
can only be restraint while being under levied load(Jiao, Borchani, Soleimani and McGraw,
2017). At the time of the construction, restraint can be given with the help of steel decking and a
reference is needed to be developed. In the perspective of non-composite beams, no positive
restraint is found regarding the compression flange. The resistance of lateral buckling only takes
place due to the friction which appears among the concrete slab and steel beams. Therefore, the
beams which support the concrete slabs can be developed as laterally restrained beams.
Conclusion
This study focuses primarily on the impact of seismic activities on various engineering
structures. It may be stated from the above study that the stability of the curved beams has been a
part in developing a better comprehension of the occurrence and the behaviour of the curved
structures with exposed to seismic disturbances. In addition to that, the Shake Table Model had
been identified as a vital model or theory in understanding the response generated by curved

BENDING STRESS IN CURVED BEAM 39
beams and such relevant structures. Furthermore, the role of expansion joints has been identified
and explored in this study. The scope for the identification of the importance of the presence of
the expansion joints within the curved beams has been discussed in this study. The overall
capacity of expansion joints, for accommodating seismic compressions, which may result in the
net movement of the curved beam from 30 to 1,200 millimeters, was noted in this paper.
SRSS was identified to be an effective technique in identifying and demonstrating the
seismic resilience of curved beams and related structures. In addition to that, the differences
between a curved beam and an arch have been discussed in this paper as well. A vivid discussion
has been made with regards to the former masonry arches as well as the new constructions
evident. The stability of the structures and the potential causes behind it has been explored as
well. It was noted that Arch of Caracalla along with other notable structures could be cited as
major examples of arches. Lastly, a discussion on the torsional buckling of beams of presented.
A discussion on the compression flange and lateral displacement with regards to the torsional
buckling of beams has been made in this paper as well.

BENDING STRESS IN CURVED BEAM 40
References
Part 1
Attary, N., Symans, M., Nagarajaiah, S., Reinhorn, A. M., Constantinou, M. C., Sarlis, A. A., ...
& Taylor, D. (2015). Performance evaluation of negative stiffness devices for seismic
response control of bridge structures via experimental shake table tests. Journal of
Earthquake Engineering, 19(2), 249-276.
Berardi, V. P., & De Piano, M. (2018). On the statics of curved masonry structures via numerical
models. PSU Research Review.
Biondini, F., Camnasio, E., & Titi, A. (2015). Seismic resilience of concrete structures under
corrosion. Earthquake Engineering & Structural Dynamics, 44(14), 2445-2466.
Di Re, P., Addessi, D., & Sacco, E. (2018). A multiscale force-based curved beam element for
masonry arches. Computers & Structures, 208, 17-31.
Franke, S., Franke, B., & Harte, A. M. (2015). Failure modes and reinforcement techniques for
timber beams–State of the art. Construction and Building Materials, 97, 2-13.
Hsu, H. L., & Halim, H. (2017). Improving seismic performance of framed structures with steel
curved dampers. Engineering Structures, 130, 99-111.
Jiang, C., Wei, B., Wang, D., Jiang, L., & He, X. (2017). Seismic vulnerability evaluation of a
three-span continuous beam railway bridge. Mathematical Problems in Engineering,
2017.

BENDING STRESS IN CURVED BEAM 41
Lemos, J. V., & Campos Costa, A. (2017). Simulation of shake table tests on out-of-plane
masonry buildings. Part (V): discrete element approach. International Journal of
Architectural Heritage, 11(1), 117-124.
Li, X. M., & Du, Y. F. (2015). The Simplified Model and the Critical Angle of the Curved
Bridges with Multi-Dimensional Earthquake Excitation. In Advanced Materials Research
(Vol. 1065, pp. 1518-1524). Trans Tech Publications.
Miyamoto, K., She, J., Imani, J., Xin, X., & Sato, D. (2016). Equivalent-input-disturbance
approach to active structural control for seismically excited buildings. Engineering
Structures, 125, 392-399.
Ni, Y., Chen, J., Teng, H., & Jiang, H. (2015). Influence of earthquake input angle on seismic
response of curved girder bridge. Journal of traffic and transportation engineering
(English edition), 2(4), 233-241.
Pydah, A., & Sabale, A. (2017). Static analysis of bi-directional functionally graded curved
beams. Composite Structures, 160, 867-876.
Sarlis, A. A., Pasala, D. T. R., Constantinou, M. C., Reinhorn, A. M., Nagarajaiah, S., & Taylor,
D. P. (2016). Negative stiffness device for seismic protection of structures: Shake table
testing of a seismically isolated structure. Journal of Structural Engineering, 142(5),
04016005.
Sorace, S., & Terenzi, G. (2016). Analysis and seismic isolation of an older reinforced concrete
vaulted building. Contemp Eng Sci, 9, 1201-1215.
Sun, P., Cui, F., Qin, H., & Hou, X. (2018). Study on Regular Inspection Frequency of Bridge
Based on Seismic Vulnerability Analysis. Shock and Vibration, 2018.

BENDING STRESS IN CURVED BEAM 42
Wang, Y. P., Lee, C. L., & Huang, S. C. (2016). Inelastic Stress Analysis of Curved Beams with
Bending and Shear Coupling. In Proceedings of the World Congress on Civil, Structural,
and Environmental Engineering (CSEE’16), Prague, Czech Republic.
Part 2
Aydin, A. C., & Özkaya, S. G. (2018). The finite element analysis of collapse loads of single-
spanned historic masonry arch bridges (Ordu, Sarpdere Bridge). Engineering
Failure Analysis, 84, 131-138.
Baek, C., Sageman-Furnas, A. O., Jawed, M. K., & Reis, P. M. (2018). Form finding in elastic
grid shells. Proceedings of the National Academy of Sciences, 115(1), 75-80.
Bertolesi, E., Milani, G., Carozzi, F.G. and Poggi, C., 2018. Ancient masonry arches and vaults
strengthened with TRM, SRG and FRP composites: Numerical
analyses. Composite Structures, 187, pp.385-402.
Borri, A., Castori, G., & Corradi, M. (2015). Strengthening of thin masonry arches. In Key
Engineering Materials (Vol. 624, pp. 51-58). Trans Tech Publications.
Cristini, H., Kauppinen-Räisänen, H., Barthod-Prothade, M., & Woodside, A. (2017). Toward a
general theory of luxury: Advancing from workbench definitions and theoretical
transformations. Journal of Business Research, 70, 101-107.
Elsayed, A., Wille, S., Al-Akhali, M., & Kern, M. (2017). Comparison of fracture strength and
failure mode of different ceramic implant abutments. The Journal of prosthetic
dentistry, 117(4), 499-506.

BENDING STRESS IN CURVED BEAM 43
Garmendia, L., Marcos, I., Garbin, E., & Valluzzi, M. R. (2014). Strengthening of masonry
arches with textile-reinforced mortar: experimental behaviour and analytical
approaches. Materials and structures, 47(12), 2067-2080.
Gosden, C., & Malafouris, L. (2015). Process archaeology (p-arch). World Archaeology, 47(5),
701-717.
Guo, Y. L., Yuan, X., Pi, Y. L., Bradford, M. A., & Chen, H. (2016). In-Plane Failure and
Strength of Pin-Ended Circular Steel Arches Considering Coupled Local and
Global Buckling. Journal of Structural Engineering, 143(1), 04016157.
Kassotakis, N., Sarhosis, V., Forgács, T., & Bagi, K. (2017). Discrete element modeling of
multi-ring brickwork masonry arches. In 13th Canadian Masonry Symposium.
Newcastle University.
Lacidogna, G., & Accornero, F. (2018). Elastic, plastic, fracture analysis of masonry arches: A
multi-span bridge case study. Curved and Layered Structures, 5(1), 1-9.
Lagomarsino, S. (2015). Seismic assessment of rocking masonry structures. Bulletin of
earthquake engineering, 13(1), 97-128.
Modena, C., Tecchio, G., Pellegrino, C., da Porto, F., Donà, M., Zampieri, P., & Zanini, M. A.
(2015). Reinforced concrete and masonry arch bridges in seismic areas: typical
deficiencies and retrofitting strategies. Structure and Infrastructure
Engineering, 11(4), 415-442.
Pulatsu, B., Erdogmus, E., & Bretas, E. M. (2018). Parametric Study on Masonry Arches Using
2D Discrete Element Modeling. Journal of Architectural Engineering, 24(2),
04018005.

BENDING STRESS IN CURVED BEAM 44
Sevim, B., Atamturktur, S., Altunişik, A. C., & Bayraktar, A. (2016). Ambient vibration testing
and seismic behavior of historical arch bridges under near and far fault ground
motions. Bulletin of Earthquake Engineering, 14(1), 241-259.
Stochino, F., Cazzani, A., Giaccu, G. F., & Turco, E. (2016, October). Dynamics of Strongly
Curved Concrete Beams by Isogeometric Finite Elements. In Conference on
Italian Concrete Days (pp. 231-247). Springer, Cham.
Sturm, J. P. (2017). Late Antique Episcopal Complexes: Bishop Eufrasius and his residence at
Poreč (Croatia). In Princes of the Church (pp. 23-33). Routledge.
Tang, M. C. (2015). The art of arches. Structure and Infrastructure Engineering, 11(4), 443-449.
Zampieri, P., Zanini, M. A., & Modena, C. (2015). Simplified seismic assessment of multi-span
masonry arch bridges. Bulletin of Earthquake Engineering, 13(9), 2629-2646.
Part 3
Badari, B., & Papp, F. (2015). On design method of lateral-torsional buckling of beams: state of
the art and a new proposal for a general type design method. Periodica Polytechnica
Civil Engineering, 59(2), 179-192.
Barnat, J., Bajer, M., Vild, M., Melcher, J., Karmazínová, M., & Piják, J. (2017). Experimental
Analysis of Lateral Torsional Buckling of Beams with Selected Cross-Section
Types. Procedia Engineering, 195, 56-61.
Barnat, J., Bajer, M., Vild, M., Melcher, J., Karmazínová, M., & Piják, J. (2017). Experimental
Analysis of Lateral Torsional Buckling of Beams with Selected Cross-Section
Types. Procedia Engineering, 195, 56-61.

BENDING STRESS IN CURVED BEAM 45
Bedon, C., Belis, J., & Amadio, C. (2015). Structural assessment and lateral–torsional buckling
design of glass beams restrained by continuous sealant joints. Engineering
Structures, 102, 214-229.
Casapulla, C., & Argiento, L. U. (2016). The comparative role of friction in local out-of-plane
mechanisms of masonry buildings. Pushover analysis and experimental investigation.
Engineering Structures, 126, 158-173.
Casapulla, C., & Argiento, L. U. (2018). In-plane frictional resistances in dry block masonry
walls and rocking-sliding failure modes revisited and experimentally validated.
Composites Part B: Engineering, 132, 197-213.
Costa, A. A., Penna, A., Arêde, A., & Costa, A. (2015). Simulation of masonry out‐of‐plane
failure modes by multi‐body dynamics. Earthquake Engineering & Structural Dynamics,
44(14), 2529-2549.
Couto, C., Real, P. V., Lopes, N., & Zhao, B. (2016). Numerical investigation of the lateral-
torsional buckling of beams with slender cross sections for the case of fire. Engineering
Structures, 106, 410-421.
Fagone, M., Ranocchiai, G., & Bati, S. B. (2015). An experimental analysis of the effects of
mortar joints on the efficiency of anchored CFRP-to-masonry reinforcements.
Composites Part B: Engineering, 76, 133-148.
Ghafoori, E., & Motavalli, M. (2015). Lateral-torsional buckling of steel I-beams retrofitted by
bonded and un-bonded CFRP laminates with different pre-stress levels: Experimental and
numerical study. Construction and Building Materials, 76, 194-206.

BENDING STRESS IN CURVED BEAM 46
Greco, F., Leonetti, L., Luciano, R., & Trovalusci, P. (2017). Multiscale failure analysis of
periodic masonry structures with traditional and fiber-reinforced mortar joints.
Composites Part B: Engineering, 118, 75-95.
Horáček, M., & Melcher, J. (2017). 05.43: Lateral‐torsional buckling of beams of double
symmetrical and mono‐symmetrical cross‐sections loaded perpendicularly to the axis of
symmetry: Experimental verification. CE/papers, 1(2-3), 1417-1426.
Horáček, M., & Melcher, J. (2017). 05.43: Lateral‐torsional buckling of beams of double
symmetrical and mono‐symmetrical cross‐sections loaded perpendicularly to the axis of
symmetry: Experimental verification. CE/papers, 1(2-3), 1417-1426.
Horáček, M., Melcher, J., Pešek, O., & Brodniansky, J. (2016). Focusing on the problem of
lateral torsional buckling of beams with web holes. Procedia engineering, 161, 549-555.
Jiao, P., Borchani, W., Soleimani, S., & McGraw, B. (2017). Lateral-torsional buckling analysis
of wood composite I-beams with the sinusoidal corrugated web. Thin-Walled
Structures, 119, 72-82.
Kala, Z. (2015). Sensitivity and reliability analyses of lateral-torsional buckling resistance of
steel beams. Archives of Civil and Mechanical Engineering, 15(4), 1098-1107.
Kala, Z., & Valeš, J. (2017). Global sensitivity analysis of lateral-torsional buckling resistance
based on finite element simulations. Engineering Structures, 134, 37-47.
Kucukler, M., Gardner, L., & Macorini, L. (2015). Flexural–torsional buckling assessment of
steel beam-columns through a stiffness reduction method. Engineering Structures, 101,
662-676.

BENDING STRESS IN CURVED BEAM 47
Kucukler, M., Gardner, L., & Macorini, L. (2015). Lateral–torsional buckling assessment of steel
beams through a stiffness reduction method. Journal of Constructional Steel
Research, 109, 87-100.
LARSSON, O. (2015). Reliability analysis. LUND University.
Leonetti, L., Greco, F., Trovalusci, P., Luciano, R., & Masiani, R. (2018). A multiscale damage
analysis of periodic composites using a couple-stress/Cauchy multidomain model:
Application to masonry structures. Composites Part B: Engineering, 141, 50-59.
Li, S., & Zeng, W. (2016). Risk analysis for the supplier selection problem using failure modes
and effects analysis (FMEA). Journal of Intelligent Manufacturing, 27(6), 1309-1321.
Lopes, G. C., Couto, C. A. R. L. O. S., Vila Real, P., & Lopes, N. U. N. O. (2016). Lateral-
torsional Buckling of Beams with Corrugated Webs Subjected to Fire. In 9th Int. Conf.
on Structures in Fire, Princeton University, SiF.
Milani, G., & Valente, M. (2015). Failure analysis of seven masonry churches severely damaged
during the 2012 Emilia-Romagna (Italy) earthquake: non-linear dynamic analyses vs.
conventional static approaches. Engineering Failure Analysis, 54, 13-56.
Naaim, N., De’nan, F., Keong, C. K., & Azar, F. (2016). Finite Element Analysis of Lateral
Torsional Buckling Behaviour of Tapered Steel Section with Perforation. In MATEC Web
of Conferences (Vol. 47, p. 02020). EDP Sciences.
Naaim, N., De’nan, F., Keong, C. K., & Azar, F. (2016). Finite Element Analysis of Lateral
Torsional Buckling Behaviour of Tapered Steel Section with Perforation. In MATEC Web
of Conferences (Vol. 47, p. 02020). EDP Sciences.

BENDING STRESS IN CURVED BEAM 48
Ozbasaran, H., & Yilmaz, T. (2018). Shape optimization of tapered I-beams with lateral-
torsional buckling, deflection and stress constraints. Journal of Constructional Steel
Research, 143, 119-130.
Ozbasaran, H., Aydin, R., & Dogan, M. (2015). An alternative design procedure for lateral–
torsional buckling of cantilever I-beams. Thin-Walled Structures, 90, 235-242.
Song, W., Ming, X., Wu, Z., & Zhu, B. (2014). A rough TOPSIS approach for failure mode and
effects analysis in uncertain environments. Quality and Reliability Engineering
International, 30(4), 473-486.
Trahair, N. S. (2017). Flexural-torsional buckling of structures. Routledge.
Vild, M., Piják, J., Barnat, J., Bajer, M., Melcher, J., & Karmazínová, M. (2017). Comparison of
analytical and numerical methods applied to lateral torsional buckling of beams. Procedia
Engineering, 195, 48-55.
Yang, B., Xiong, G., Ding, K., Nie, S., Zhang, W., Hu, Y., & Dai, G. (2016). Experimental and
numerical studies on lateral-torsional buckling of GJ structural steel beams under a
concentrated loading condition. International Journal of Structural Stability and
Dynamics, 16(01), 1640004.