STAT102 Business Data Analysis: Facts from Figures Assignment
VerifiedAdded on 2022/11/25
|7
|677
|229
Homework Assignment
AI Summary
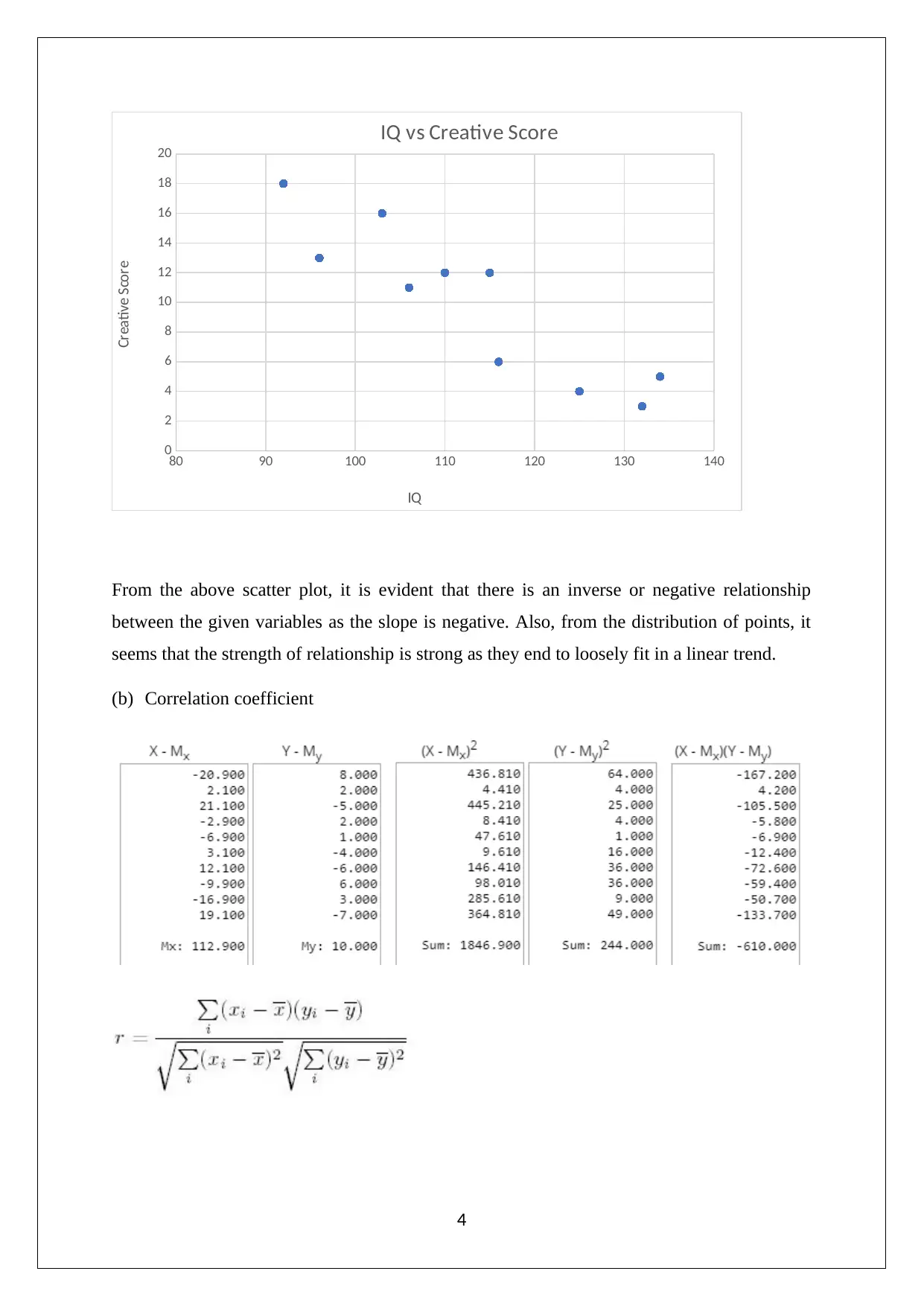
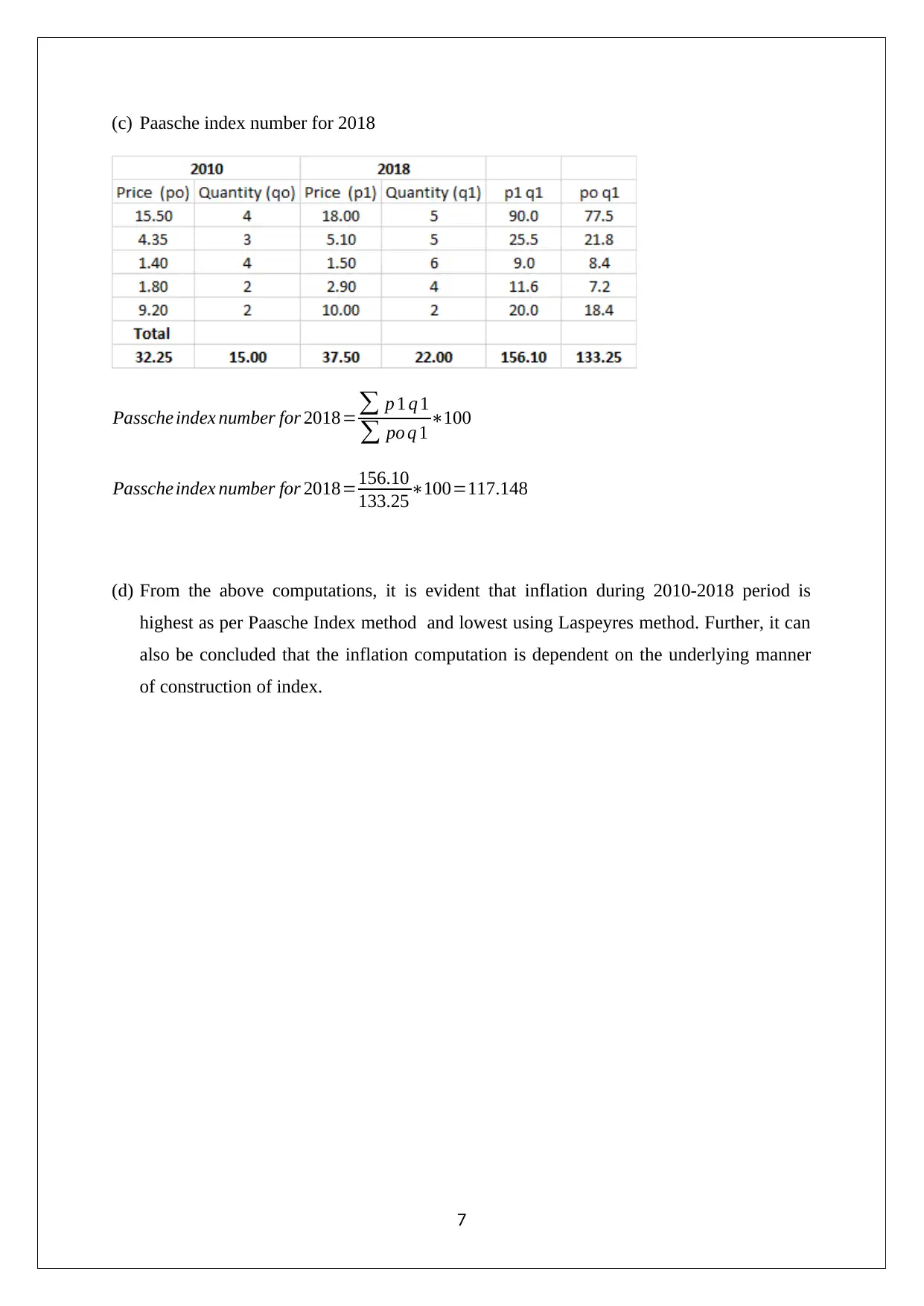
This document presents a complete solution to a STAT102 Business Data Analysis assignment from Peter Faber Business School. The assignment covers several key concepts, starting with an analysis of sampling bias in a car sales scenario, contrasting probability and non-probability sampling. It then includes a tree diagram analysis, followed by the calculation of a 95% confidence interval for the mean time spent sleeping by students using sample data. The solution continues with a scatter plot analysis to determine the relationship between variables and the calculation of the correlation coefficient, including hypothesis testing to assess the significance of the linear relationship. Finally, the assignment concludes with the calculation of unweighted aggregate price indices, including both Laspeyres and Paasche index methods, to illustrate the impact of different calculation methods on inflation measurement.
1 out of 7












![[object Object]](/_next/static/media/star-bottom.7253800d.svg)