Control and Instrumentation: System Modeling, Analysis, and Control
VerifiedAdded on 2020/01/28
|53
|3958
|272
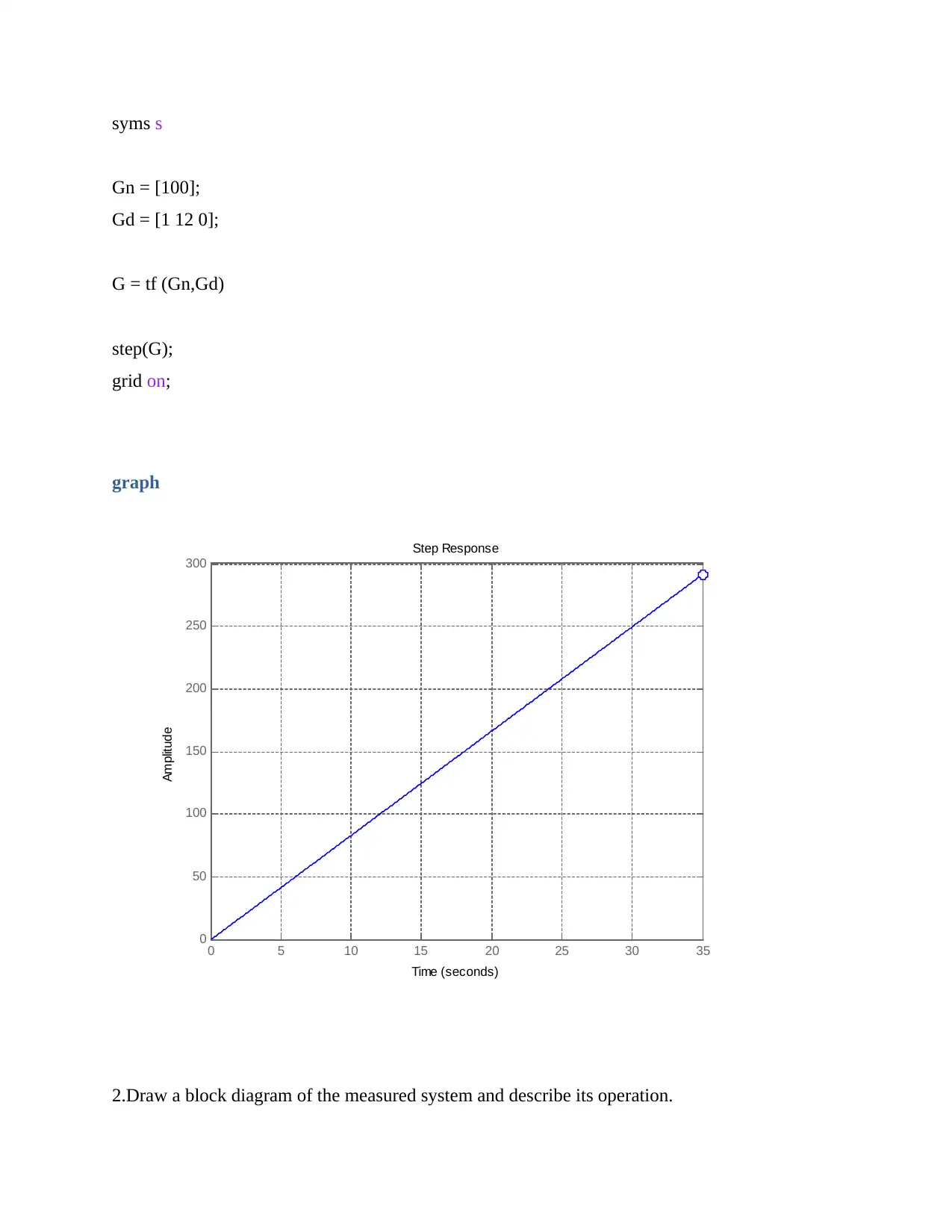
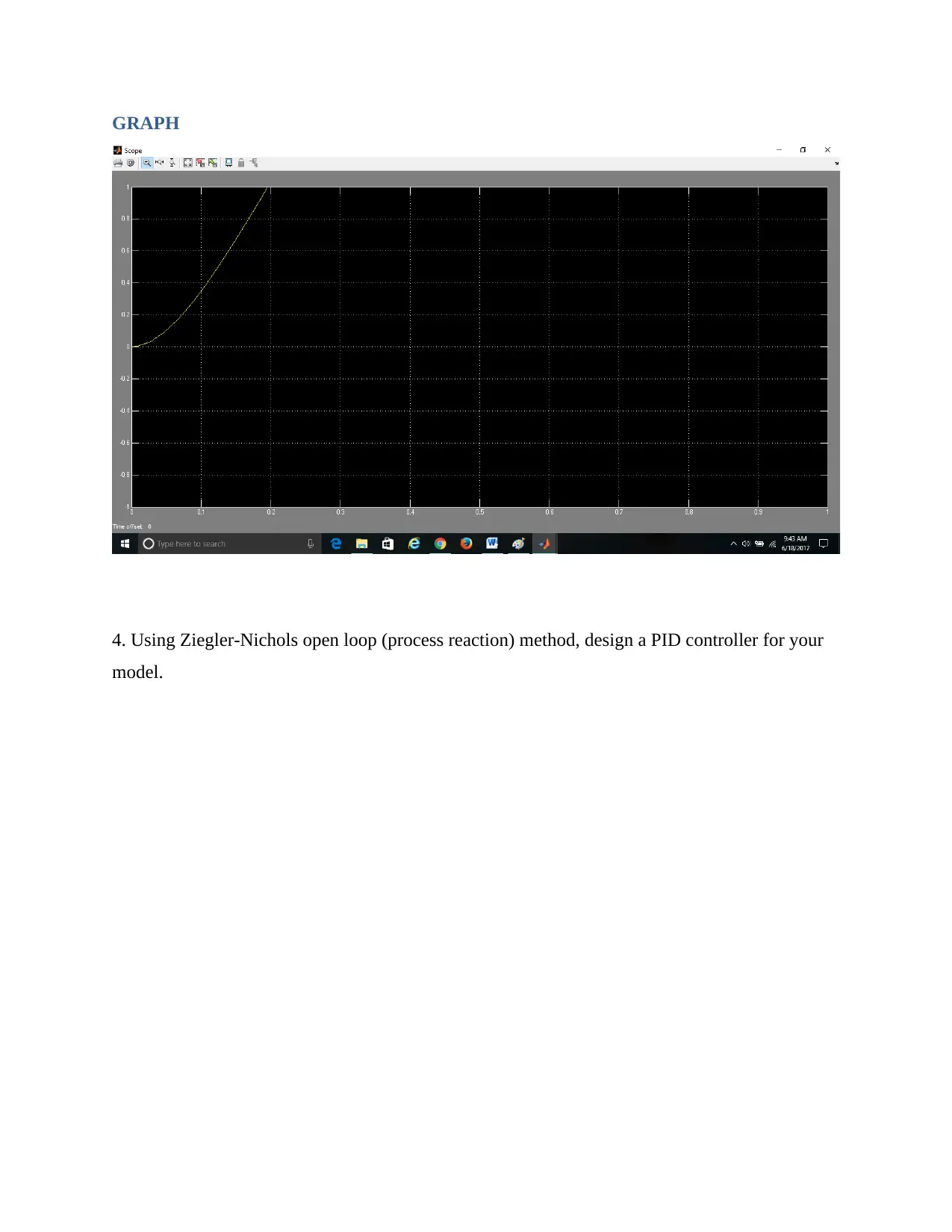
Practical Assignment
AI Summary
This assignment delves into the principles of control and instrumentation, covering both open and closed-loop systems. The solution begins with obtaining and analyzing step response data from a second-order, linear time-invariant (LTI) open-loop system, followed by the creation of a block diagram and a detailed explanation of its operation. The system is then modeled in MATLAB and Simulink, with the output response to a step input accurately mimicking the real system. PID controllers are designed using the Ziegler-Nichols open-loop (process reaction) method, and the system is modeled as a closed-loop system. The closed-loop system's output response to a step input is tested and verified. Furthermore, the expected frequency response of the open-loop system is calculated, considering low and high frequencies, poles, zeros, and dB frequency. The Simulink model is used to simulate the system and obtain output frequency data in the form of Bode and Nyquist plots. The Simulink results are compared with the calculated results, critically evaluating the model's accuracy. Part B extends the analysis, employing root locus methods for PID controller design and providing comparative analysis of the Ziegler-Nichols and root locus methods. The assignment includes MATLAB code, Simulink models, and graphical representations to illustrate the concepts and results.
1 out of 53










![[object Object]](/_next/static/media/star-bottom.7253800d.svg)