Cryptography Tutorial with Examples and Exercises - Desklib

This document contains solved examples and exercises on Cryptography. It covers various topics like Caesar Cipher, Transposition Cipher, Vigenere Autokey Method and more. It also includes solved assignments, essays, dissertations and more on Cryptography.

Running head: CRYPTOGRAPHY
CRYPTOGRAPHY
Name of the Student
Name of the University
Author Note

CRYPTOGRAPHY 1
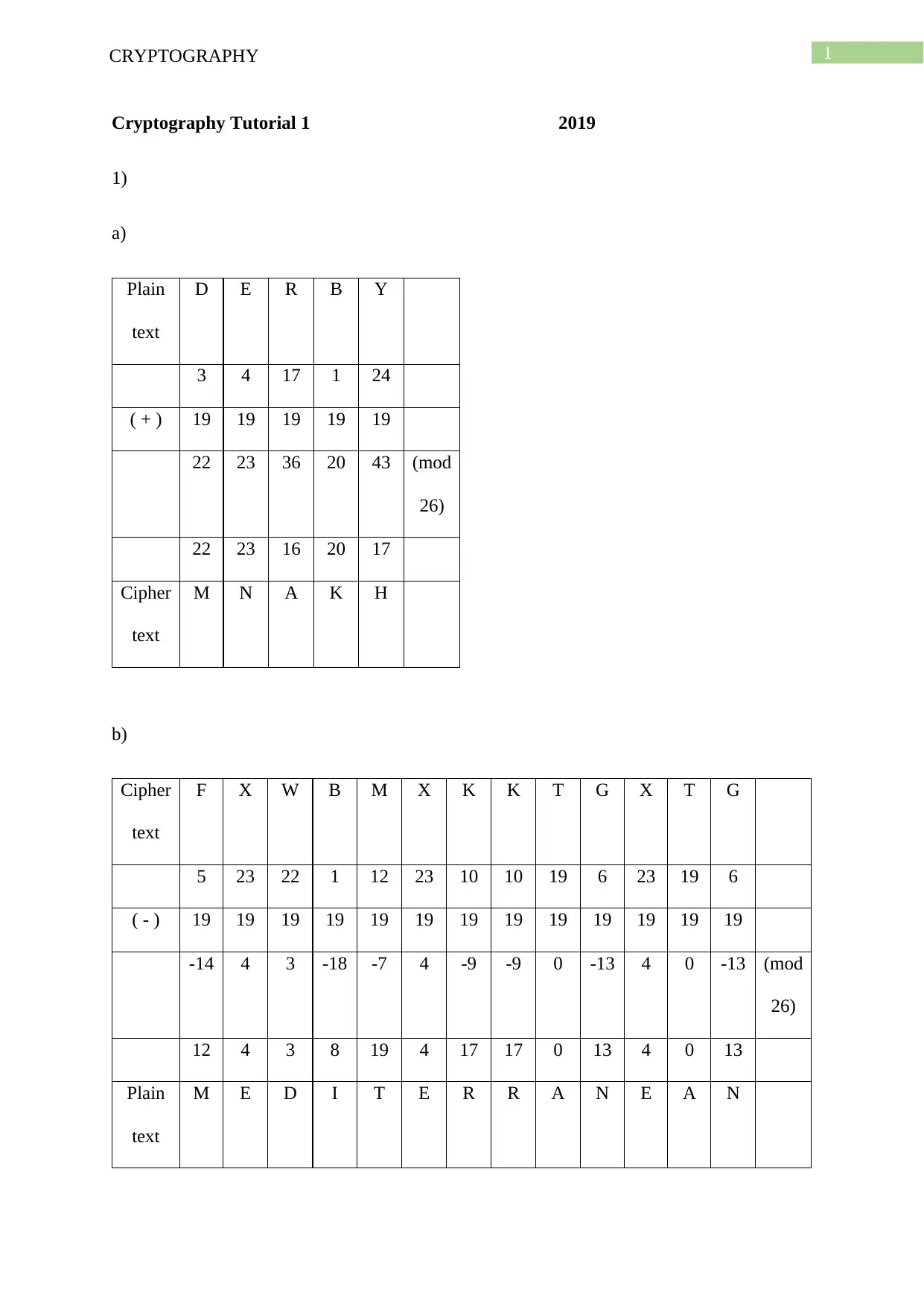
Cryptography Tutorial 1 2019
1)
a)
Plain
text
D E R B Y
3 4 17 1 24
( + ) 19 19 19 19 19
22 23 36 20 43 (mod
26)
22 23 16 20 17
Cipher
text
M N A K H
b)
Cipher
text
F X W B M X K K T G X T G
5 23 22 1 12 23 10 10 19 6 23 19 6
( - ) 19 19 19 19 19 19 19 19 19 19 19 19 19
-14 4 3 -18 -7 4 -9 -9 0 -13 4 0 -13 (mod
26)
12 4 3 8 19 4 17 17 0 13 4 0 13
Plain
text
M E D I T E R R A N E A N

2CRYPTOGRAPHY
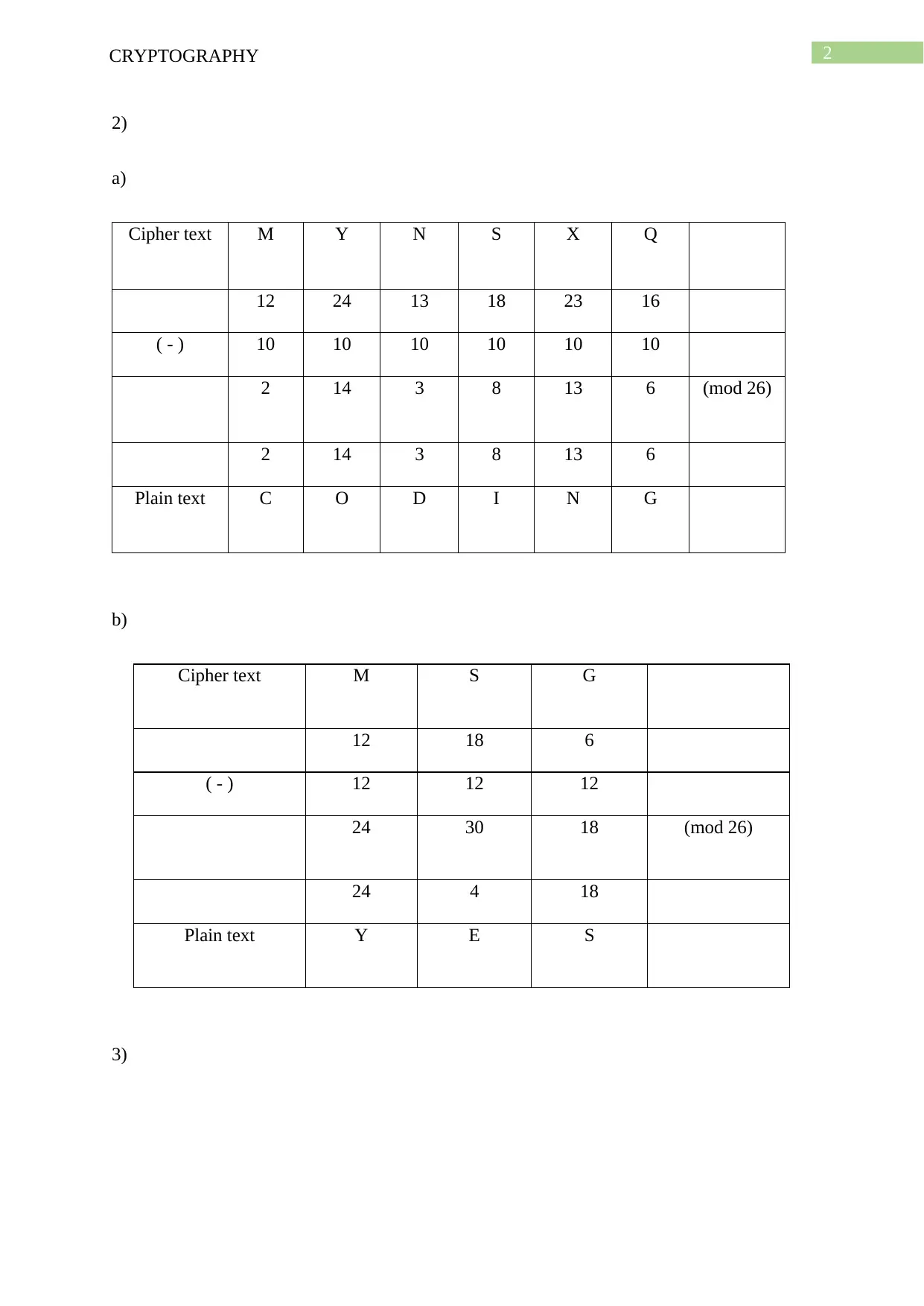
2)
a)
Cipher text M Y N S X Q
12 24 13 18 23 16
( - ) 10 10 10 10 10 10
2 14 3 8 13 6 (mod 26)
2 14 3 8 13 6
Plain text C O D I N G
b)
Cipher text M S G
12 18 6
( - ) 12 12 12
24 30 18 (mod 26)
24 4 18
Plain text Y E S
3)

3CRYPTOGRAPHY
Plain
text
K E D L E S T O N R O A D
Key FINAL YEAR STUDENT
Cipher
text
U L A D L M O G C K G F A
4) REVERSE ALPHABET
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Z Y X W V U T S R Q P O N M L K J I H G F E D C B A
Plain
text
T H E S S A L O N I K I
Cipher
text
G S V H H Z O L M R P R
Cryptography Tutorial 2
1)
Message ten green bottles hanging on the wall
Key KEDLESTON ROAD

4CRYPTOGRAPHY
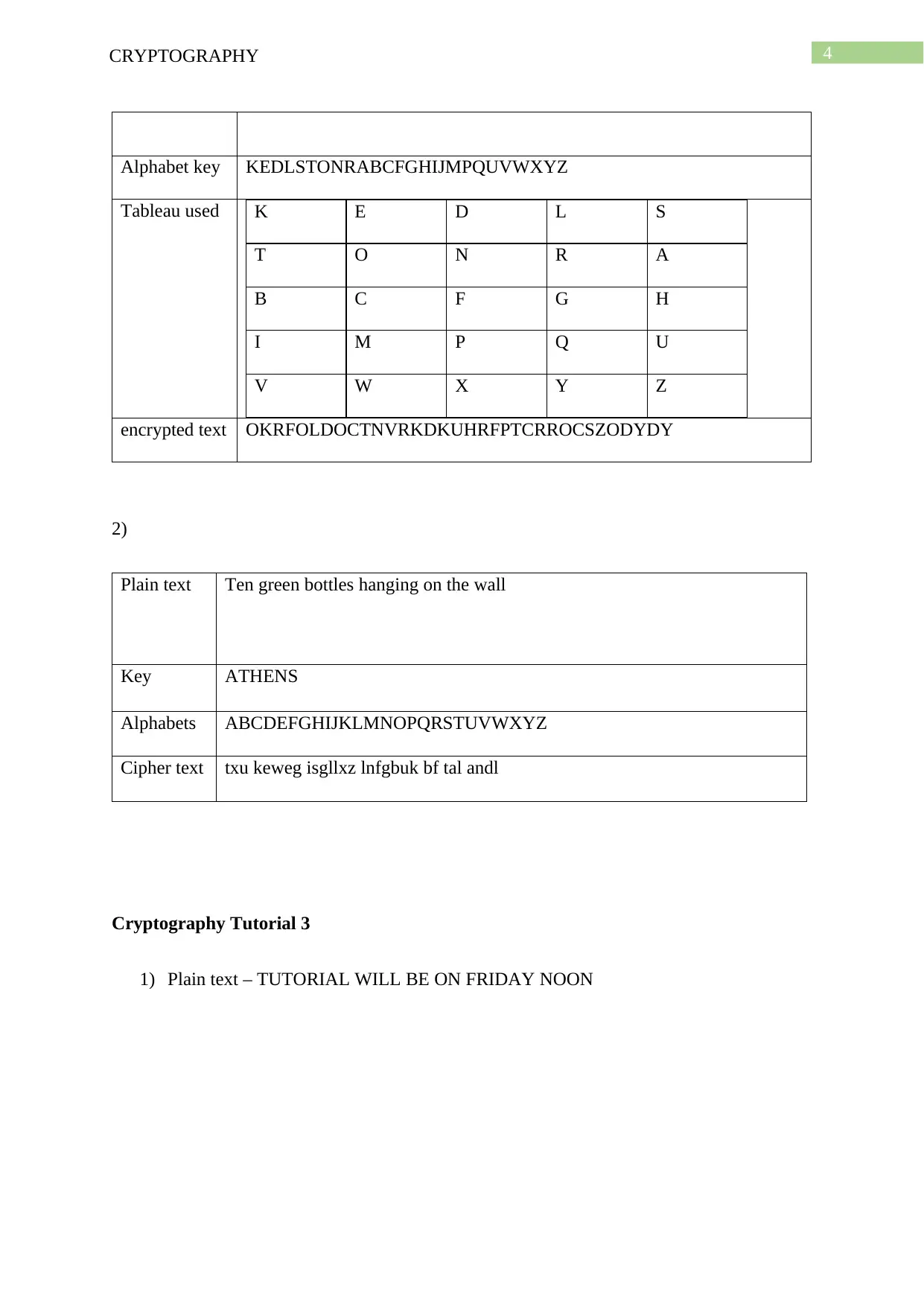
Alphabet key KEDLSTONRABCFGHIJMPQUVWXYZ
Tableau used K E D L S
T O N R A
B C F G H
I M P Q U
V W X Y Z
encrypted text OKRFOLDOCTNVRKDKUHRFPTCRROCSZODYDY
2)
Plain text Ten green bottles hanging on the wall
Key ATHENS
Alphabets ABCDEFGHIJKLMNOPQRSTUVWXYZ
Cipher text txu keweg isgllxz lnfgbuk bf tal andl
Cryptography Tutorial 3
1) Plain text – TUTORIAL WILL BE ON FRIDAY NOON

5CRYPTOGRAPHY
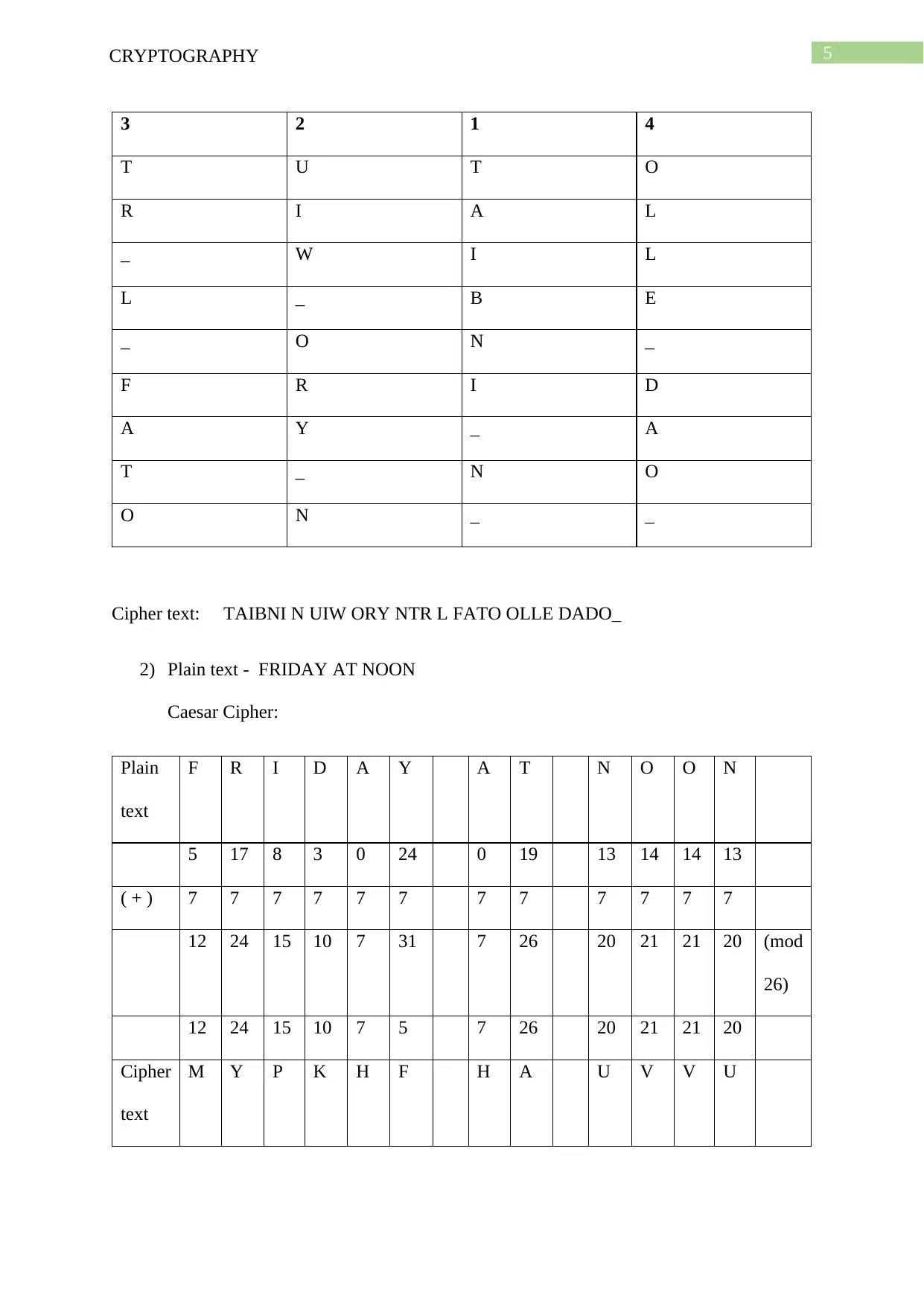
3 2 1 4
T U T O
R I A L
_ W I L
L _ B E
_ O N _
F R I D
A Y _ A
T _ N O
O N _ _
Cipher text: TAIBNI N UIW ORY NTR L FATO OLLE DADO_
2) Plain text - FRIDAY AT NOON
Caesar Cipher:
Plain
text
F R I D A Y A T N O O N
5 17 8 3 0 24 0 19 13 14 14 13
( + ) 7 7 7 7 7 7 7 7 7 7 7 7
12 24 15 10 7 31 7 26 20 21 21 20 (mod
26)
12 24 15 10 7 5 7 26 20 21 21 20
Cipher
text
M Y P K H F H A U V V U

6CRYPTOGRAPHY
Transposition cipher:
1 2 3 4 5
F R I D A
Y _ A T _
N O O N _
Key- 52341
Cipher text: ARIDF___ATY_OONN
1) MATRIX ADDITION:
i. AG - Addition is not possible because dimension of A is 1*6 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
ii. AB - Addition is not possible because dimension of A is 1*6 and for B is 3*1 and
in matrix addition it is not possible to add two matrix with different dimension.
iii. GA- Addition is not possible because dimension of A is 1*6 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
iv. GB - Addition is not possible because dimension of B is 3*1 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
v. CG - Addition is not possible because dimension of C is 1*3 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
vi. GC - Addition is not possible because dimension of C is 1*3 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
vii. DG - Addition is not possible because dimension of D is 3*3 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.

7CRYPTOGRAPHY
viii. GD - Addition is not possible because dimension of D is 3*3 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
ix. EG - Addition is not possible because dimension of E is 1*3 and for G is 3*6 and
in matrix addition it is not possible to add two matrix with different dimension.
x. EF –
E = [0 0 1] F = [0 1 0]
EF = [ 0+0 0+1 1+0 ] = [ 0 1 1 ]
2)
i. 1010+0111 = 10001
ii. 100+001 = 101
iii.
Decimal Binary
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
iv. 1010+1011+0000 = 10101
3)

8CRYPTOGRAPHY
i. 0101+1110 = 1011
ii. 0001+1011 = 1010
iii. 000111001+111010101 = 111101100
iv. 01010101+01010101 = 0
CRYPTOGRAPHY EXERCISES:
Exercise 1:
Caesar cipher:
Plain
text
A T H E N S I S I N G R E E C E
Shift
Key
6
Cipher
text
G Z N K T Y O Y O T M X K K I T
Transposition cipher:
1 2 3 4
G Z N K
T Y _ O
Y _ O T
M X K K
I T Z Z
Cipher text: GTYMIZY_XTN_OKZKOTKZ

9CRYPTOGRAPHY
Exercise 2:
Plain text- upuvueplepononieoeuxuhxv
Key- TALKING
Play fair square-
Cipher text- support needed tomorrow
Exercise-3
1)
1 2 3 4 5
M E E T I
N G W I
L L B E
O N S
U N D A Y
A T T W
E L V E
Key– 32451
T A L K I
N G B C D
E F H M O
P Q R S U
V W X Y Z

10CRYPTOGRAPHY
3 2 4 5 1
E E T I M
G W I N
L B E L
N O S
D N A Y U
T A T W
V L E E
Cipher text- EETIM GWIN S DNAYUTA T LEVEW
2).
1 2 3 4 5 6
P E I T G H
C N I P P E
S R U H B E
T I U S T T
N O E E S S
O B L Y F M
A E C O H R
T T E L R E

11CRYPTOGRAPHY
Order applied- 4 6 2 1 3 5
4 6 2 1 3 5
T H E P I G
P E N C I P
H E R S U B
S T I T U T
E S O N E S
Y M B O L F
O R E A C H
L E T T E R
Plain text- THE PIG PEN CIPHER SUBSTITUTES ONE SYMBOL FOR EACH LETTER
Exercise 4:
Vigenere autokey method:
In autokey method, the term autokey means the key that is depending on the actual
plaintext. Actually this is extension of the vigenere cipher, makes the cipher text harder to
break. In this method, the passphrase is used only once and the clear text is used to encrypt or
decrypt the text instead of using that repeatedly.
Plain text: cryptography is fab
Key: S
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

12CRYPTOGRAPHY
B B C D E F G H I J K L M N O P Q R S T U V W X Y Z A
C C D E F G H I J K L M N O P Q R S T U V W X Y Z A B
D D E F G H I J K L M N O P Q R S T U V W X Y Z A B C
E E F G H I J K L M N O P Q R S T U V W X Y Z A B C D
F F G H I J K L M N O P Q R S T U V W X Y Z A B C D E
G G H I J K L M N O P Q R S T U V W X Y Z A B C D E F
H H I J K L M N O P Q R S T U V W X Y Z A B C D E F G
I I J K L M N O P Q R S T U V W X Y Z A B C D E F G H
J J K L M N O P Q R S T U V W X Y Z A B C D E F G H I
K K L M N O P Q R S T U V W X Y Z A B C D E F G H I J
L L M N O P Q R S T U V W X Y Z A B C D E F G H I J K
M M N O P Q R S T U V W X Y Z A B C D E F G H I J K L
N N O P Q R S T U V W X Y Z A B C D E F G H I J K L M
O O P Q R S T U V W X Y Z A B C D E F G H I J K L M N
P P Q R S T U V W X Y Z A B C D E F G H I J K L M N O
Q Q R S T U V W X Y Z A B C D E F G H I J K L M N O P
R R S T U V W X Y Z A B C D E F G H I J K L M N O P Q
S S T U V W X Y Z A B C D E F G H I J K L M N O P Q R
T T U V W X Y Z A B C D E F G H I J K L M N O P Q R S

13CRYPTOGRAPHY
U U V W X Y Z A B C D E F G H I J K L M N O P Q R S T
V V W X Y Z A B C D E F G H I J K L M N O P Q R S T U
W W X Y Z A B C D E F G H I J K L M N O P Q R S T U V
X X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Y Y Z A B C D E F G H I J K L M N O P Q R S T U V W X
Z Z A B C D E F G H I J K L M N O P Q R S T U V W X Y
Cipher text: utpnihuxrpwf ga xfb
Vigenere keyword method vs vigenere autokey method:
Vigenere Cipher is a method of encrypting alphabetic text. It uses a simple form of
polyalphabetic substitution. A polyalphabetic cipher is any cipher based on substitution,
using multiple substitution alphabets .The encryption of the original text is done using the
Vigenère square or Vigenère table.
In autokey method, the term autokey means the key that is depending on the actual plaintext.
Actually this is extension of the vigenere cipher, makes the cipher text harder to break. In this
method, the passphrase is used only once and the clear text is used to encrypt or decrypt the
text instead of using that repeatedly.
The autokey method is more secure because it is depending on the actual plaintext and it is an
extension to the vigenere cipher, which makes the cipher text harder to break.
Part 2:

14CRYPTOGRAPHY
Cipher text:
WLVCMBTRTQHHRMJWLVBQVMXOKHRKT
W L V C M B T R T Q H H R M J W L V B Q V M X O K H R K T
W L V C M B T R T Q H H R M J W L V B Q V M X O K H R K
W L V C M B T R T Q H H R M J W L V B Q V M X O K H R
W L V C M B T R T Q H H R M J W L V B Q V M X O K H
W L V C M B T R T Q H H R M J W L V B Q V M X O K
W L V C M B T R T Q H H R M J W L V B Q V M X O
W L V C M B T R T Q H H R M J W L V B Q V M X
W L V C M B T R T Q H H R M J W L V B Q V M
W L V C M B T R T Q H H R M J W L V B Q V
W L V C M B T R T Q H H R M J W L V B Q
W L V C M B T R T Q H H R M J W L V B
W L V C M B T R T Q H H R M J W L V
W L V C M B T R T Q H H R M J W L
W L V C M B T R T Q H H R M J W
W L V C M B T R T Q H H R M J
W L V C M B T R T Q H H R M
W L V C M B T R T Q H H R
W L V C M B T R T Q H H
W L V C M B T R T Q H
W L V C M B T R T Q
W L V C M B T R T
W L V C M B T R
W L V C M B T
W L V C M B
W L V C M
W L V C
W L V
W L
W
Possible key length applied- 5
Plain text: THE BOY PASSED ALL THE ASSIGNMENTS
Method applied: vigenere cipher.
Exercise 5:
1)
Letter No of times Percentage

15CRYPTOGRAPHY
Q 69× 11.48%
H 65× 10.82%
Z 62× 10.32%
G 52× 8.65%
U 45× 7.49%
V 41× 6.82%
C 37× 6.16%
F 33× 5.49%
S 26× 4.33%
A 25× 4.16%
W 24× 3.99%
X 20× 3.33%
Y 17× 2.83%
R 17× 2.83%
T 16× 2.66%
D 12× 2%
N 10× 1.66%
J 7× 1.16%
K 6× 1%
B 5× 0.83%
M 5× 0.83%
P 4× 0.67%
I 2× 0.33%
L 1× 0.17%

16CRYPTOGRAPHY
2)
Letter No of times Percentage
K 17× 10.37%
E 15× 9.15%
B 14× 8.54%
Q 13× 7.93%
T 11× 6.71%
W 11× 6.71%
H 11× 6.71%
Z 11× 6.71%
O 9× 5.49%
D 7× 4.27%
F 6× 3.66%
C 5× 3.05%
X 5× 3.05%
A 5× 3.05%
S 5× 3.05%
N 4× 2.44%
G 4× 2.44%
P 3× 1.83%
V 3× 1.83%
Y 2× 1.22%
I 2× 1.22%

17CRYPTOGRAPHY
M 1× 0.61%
Coding tutorial 1:
1)
i. Wt (010 011 110 101) – here the number of 1’s is 7 so, the wt is 7.
ii. Wt (011 011 101 000) - here the number of 1’s is 6 so, the wt is 6.
2)
The difference between these two binary words wt (010 011 110 101) and (011 011 101 000)
is 5.
010 011 110 101
011 011 101 000
3) D (w, w) in w means the distance between the given binary words and here the distance is
0, as the binary numbers are same.
4)
1. The safe route is 11 01 01 11 01 11 11 11 11 11 01 01 00 00
2. The safe route is 110 011 011 110 011 110 110 110 110 110 011 011 000 000
3. The safe route is 11011 01101 01101 11011 01101 11011 11011 11011 11011 11011
00000 00000
4)
00110011
01101101

18CRYPTOGRAPHY
01010110
01010011
The minimum distance is – 7
5)
i.
111010+110101 = 1111
1111+010011 = 11100
11100+010011 = 1111
1111+11100 = 10011
10011+110110 = 100101
ii. The length of this code 100101 is – 3.

19CRYPTOGRAPHY
Bibliography:
Falkowski, B.J. and Perkowski, M.A., 1990, May. A family of all essential radix-2
addition/subtraction multi-polarity transforms: algorithms and interpretations in Boolean
domain. In IEEE International Symposium on Circuits and Systems(pp. 2913-2916). IEEE.
Goyal, K. and Kinger, S., 2013. Modified Caesar Cipher for Better Security
Enhancement. International Journal of Computer Ap Kester, Q.A., 2013. A Hybrid
Cryptosystem based on Vigenere cipher and Columnar Transposition cipher. arXiv preprint
arXiv:1307.7786.plications, 73(3), pp.0975-8887.
Heydari, M., Shabgahi, G.L. and Heydari, M.M., 2013. Cryptanalysis of transposition ciphers
with long key lengths using an improved genetic algorithm. World Applied Sciences
Journal, 21(8), pp.1194-1199.
Li, C., Liu, Y., Zhang, L.Y. and Chen, M.Z., 2013. Breaking a chaotic image encryption
algorithm based on modulo addition and XOR operation. International Journal of
Bifurcation and Chaos, 23(04), p.1350075.
Ray, S., Bhaumik, A., Pramanik, M., Butcher, R.J., Yildirim, S.O. and Mukhopadhyay, C.,
2014. Binary conjugate Brønsted–Lewis acid supported on mesoporous silica nanoparticles
for the domino addition/elimination/addition and addition/elimination/addition/cyclization
cascade. Catalysis Communications, 43, pp.173-178.
Tripathi, R. and Agrawal, S., 2014. Comparative study of symmetric and asymmetric
cryptography techniques. International Journal of Advance Foundation and Research in
Computer (IJAFRC), 1(6), pp.68-76.