Data Structures and Algorithms: Problem Solving and Analysis
VerifiedAdded on 2023/06/10
|16
|1240
|91
Homework Assignment
AI Summary
This assignment solution addresses various concepts within Data Structures and Algorithms. It begins with an introduction to algorithms and data structures, followed by the analysis of greedy criteria and their limitations in activity selection. The solution then delves into the Ford-Fulkerson algorithm, illustrating its application through residual graphs and maximum flow computations. Further, it explores binary search trees, including their properties, best and worst-case scenarios, and motivations for their use. The assignment also examines binomial trees and deletion operations. Finally, it covers binary search in sorted arrays, dynamic programming, and the NP-completeness of the traveling salesman problem, offering detailed explanations and analysis of each concept.
1 out of 16





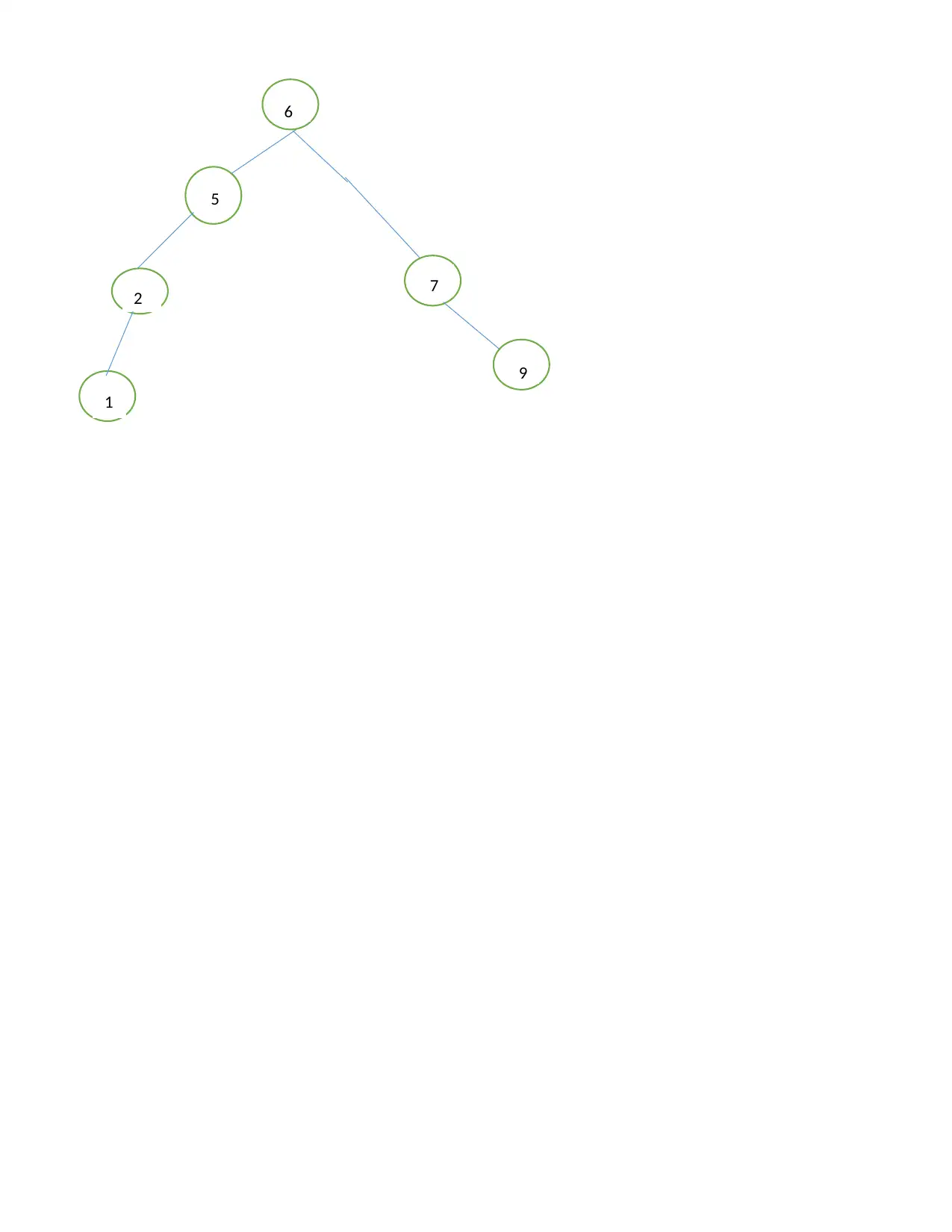
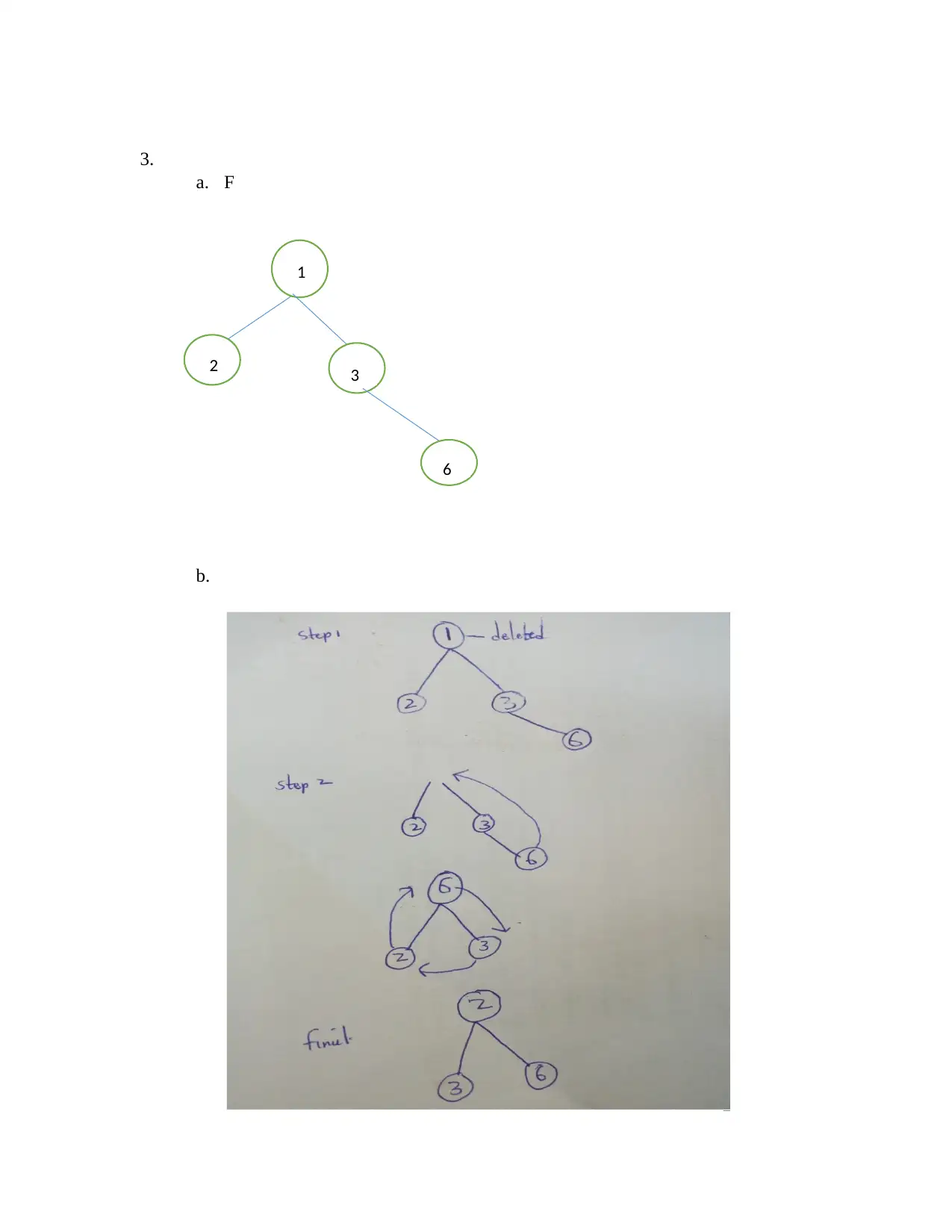
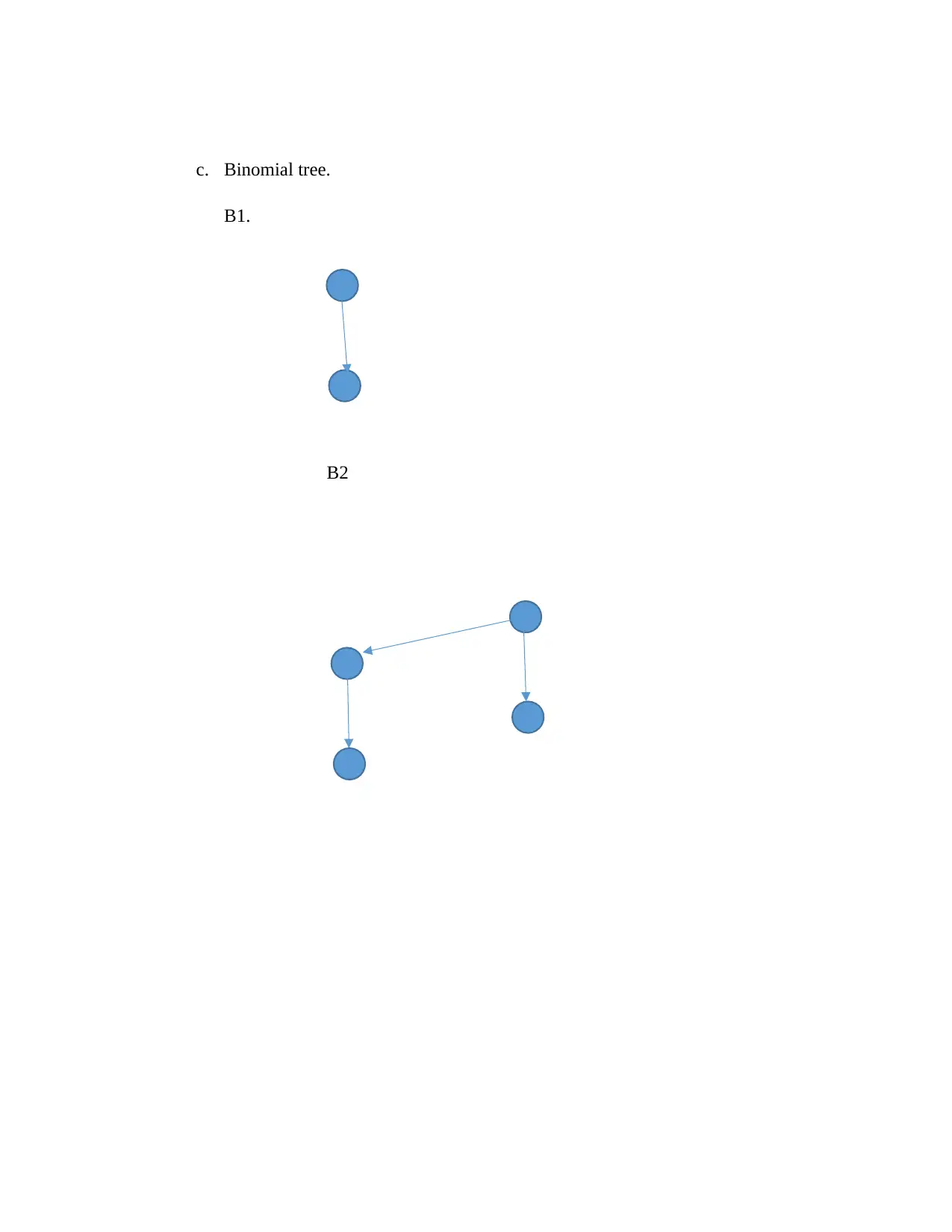
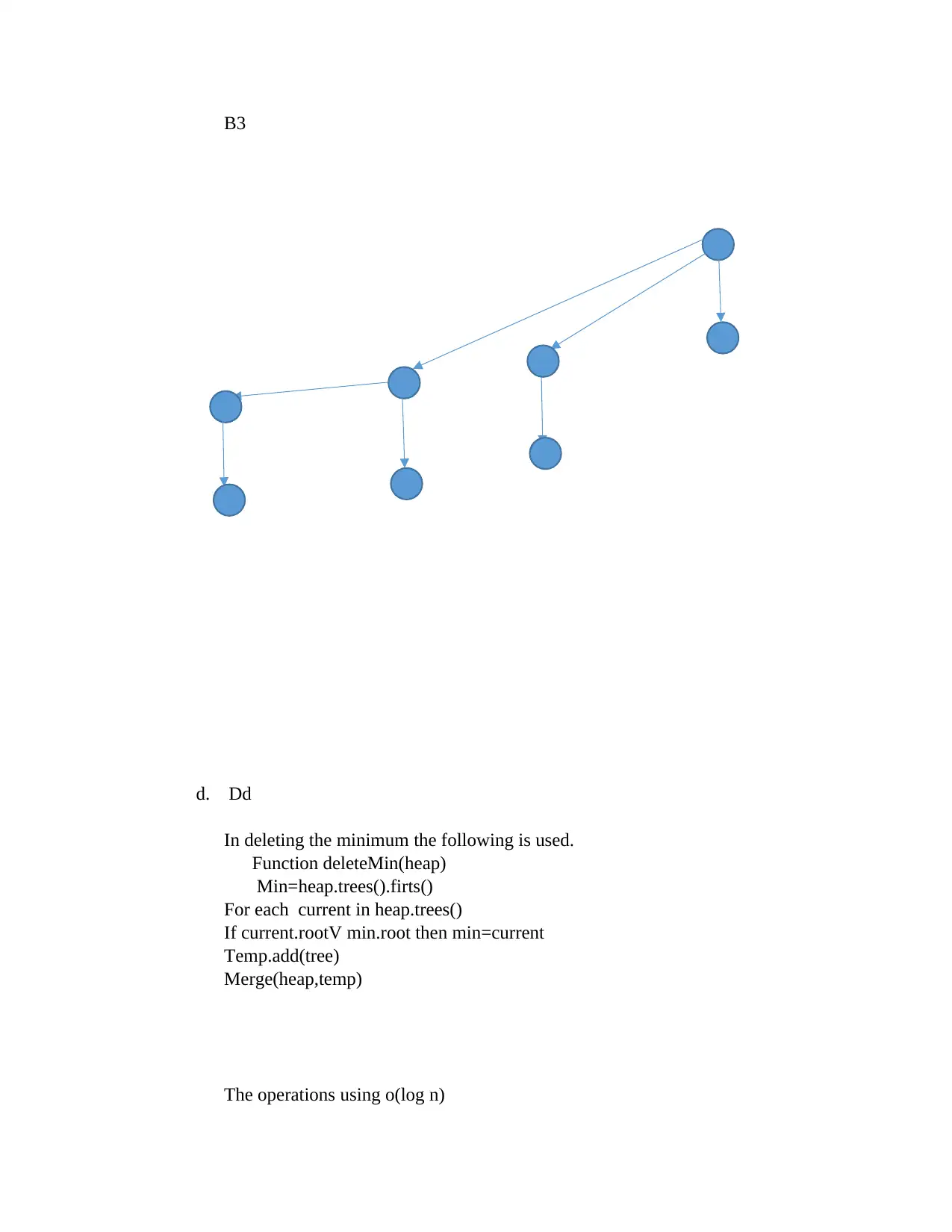






![[object Object]](/_next/static/media/star-bottom.7253800d.svg)