Faculty of Technology: DC Motor Modelling and Control Report

This report presents a detailed analysis of DC motor modeling and control, encompassing three key sections. Section A focuses on DC motor modeling, including the equivalent circuit diagram, calculations of armature resistance, and the simulation of back EMF and armature current using Simulink. The report determines the armature inductance based on the motor's response to a voltage step. Section B explores the motor's drive characteristics, including the differential equation governing the motor's behavior, and the determination of stalling torque through Simulink simulations. Finally, Section C investigates speed control using an integral control system, including the design of the control system, and the determination of the integral constant (KI) to achieve a desired speed overshoot. The report concludes with the analysis of speed curves under varying set points, demonstrating the effectiveness of the control strategy. The assignment is a coursework report for the Faculty of Technology EAT216 CAE module.

Running head: DC MOTOR MODELLING AND CONTROL
DC MOTOR MODELLING AND CONTROL
Name of the Student
Name of the University
Author Note

1DC MOTOR MODELLING AND CONTROL
Section A: DC Motor Modelling
1. The equivalent circuit diagram of separately excited DC motor is given below.
The field resistance Rf = 75 Ω.
Field inductance Lf = 50 H
Back emf constant Ke = 0.5
J = moment of inertia of drive = 0.2 kgm^2
B = frictional coefficient of drive system = 0.067 kgm^2/s
Here, Va = armature voltage (V)
Ia = armature current (A)
Ea = back EMF produced at the Armature
Vf = DC field voltage and If = current (A)
Te = electrical drive torque and Tl = load torques (Nm)
ω = drive speed in rads/sec.

2DC MOTOR MODELLING AND CONTROL
Ra = armature resistance, La = armature inductance, Rf = Field resistance, Lf = field
inductance.
Hence, by using the KVL analysis
Va = V(Ra) + V(La) + Ea
 Va = Ia*Ra + Ia*(dIa/dt) + Ea.
Now, the value of Ra = (2*(xyz/999) + 1). Here, ‘xyz’ is 304.
Hence, Ra = 2*304/999 + 1 = 1.6086 Ω.
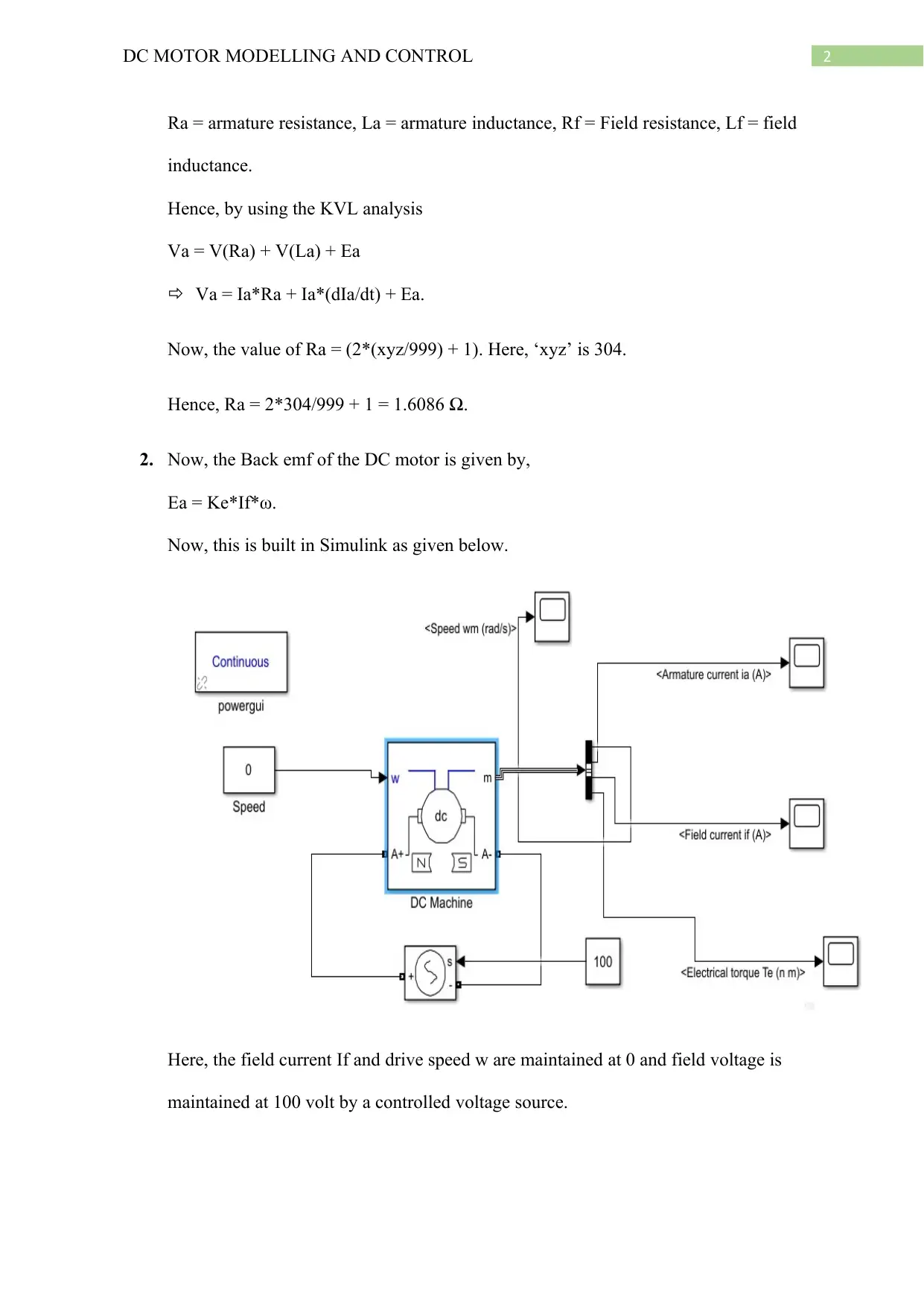
2. Now, the Back emf of the DC motor is given by,
Ea = Ke*If*ω.
Now, this is built in Simulink as given below.
Here, the field current If and drive speed w are maintained at 0 and field voltage is
maintained at 100 volt by a controlled voltage source.

3DC MOTOR MODELLING AND CONTROL
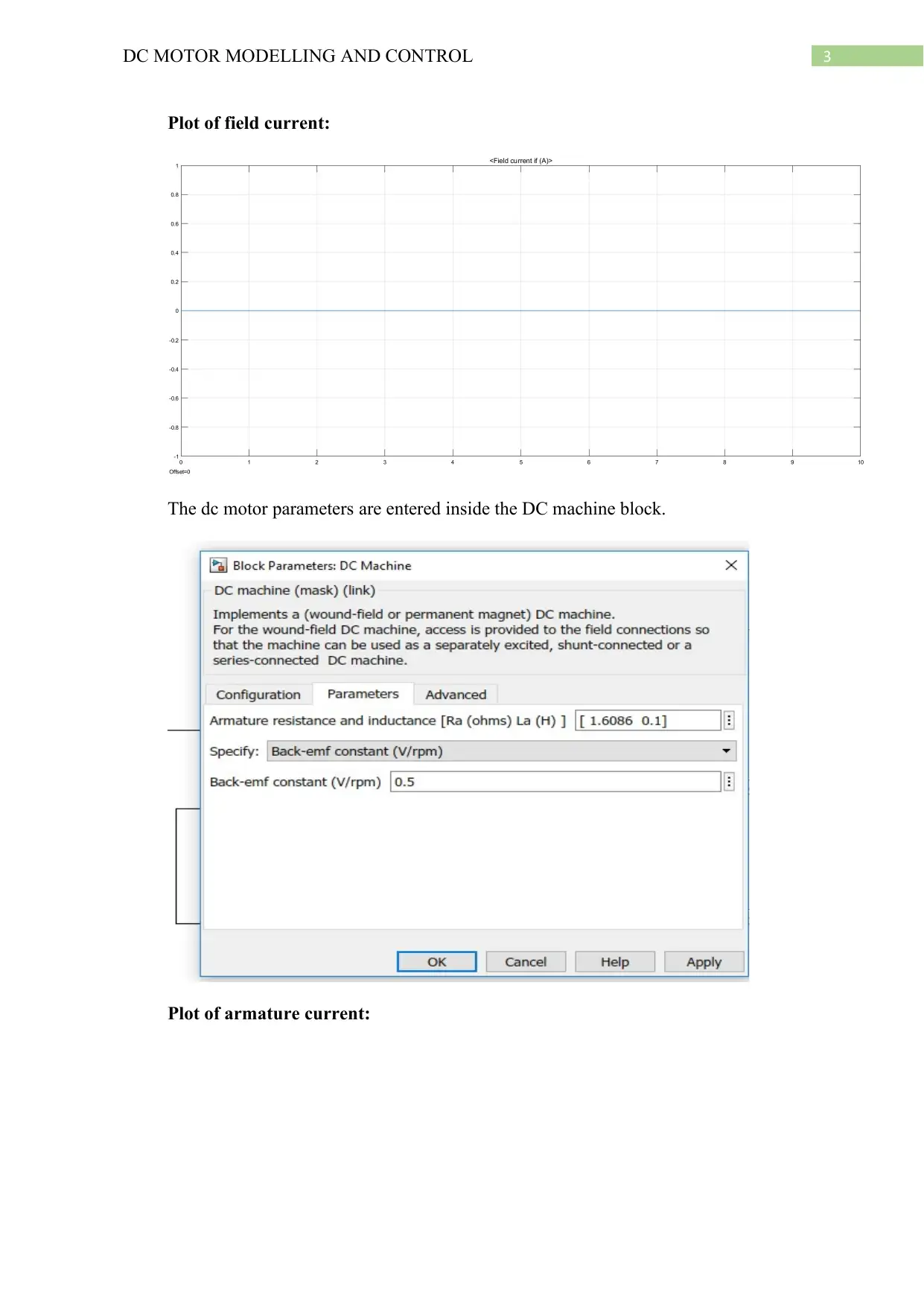
Plot of field current:
The dc motor parameters are entered inside the DC machine block.
Plot of armature current:

4DC MOTOR MODELLING AND CONTROL
Hence, the steady state value of armature current is 62.16 Amps as found from the
simulation scope.
3. Now, in a particular simulation, it is found that the armature current reached 63.2% of
its final value in 5 msec or 0.005 sec. Now, the armature inductance La is needed to
found for that simulation.
In this question trial and error method (where armature inductance La is varied) is
applied to find the approximate simulation and then the value of La which gives close
to 63.2% of final armature current in 0.005 sec is recorded here.
Now, 63.2% of final armature current = 62.15*0.632 = 39.2788.
Now, simulating the waveform at La = 0.0015 H gives an approximate of the
specified value of armature current.

5DC MOTOR MODELLING AND CONTROL
Hence, the value of the armature inductance for which the armature current reaches
63.2% at 0.005 sec is 0.0015 H.
4. The equation A1 is given by,
Va=Ea+Ia∗Ra+La∗( dIa
dt )
Now, the armature current is maximum when the back Emf of the motor is zero and
inductance is zero. This happens at the start of the motor. Hence, at the start the
armature current is given by, Ia = Va/Ra = 100 / 1.6086 = 62.1659 Amps.
Now, the armature inductance La can be calculated by the following procedure.
The inductance in armature coil is given by,
L = N*Ф/I,
Where, N = number of turns in the coil
Ф = entire magnetic flux in Weber, Wb
A = cross sectional area of coil.
Section B:
1.
The given differential equation of the motor’s drive is given by,
Te = J*(dω/dt) + Bω + TL

6DC MOTOR MODELLING AND CONTROL
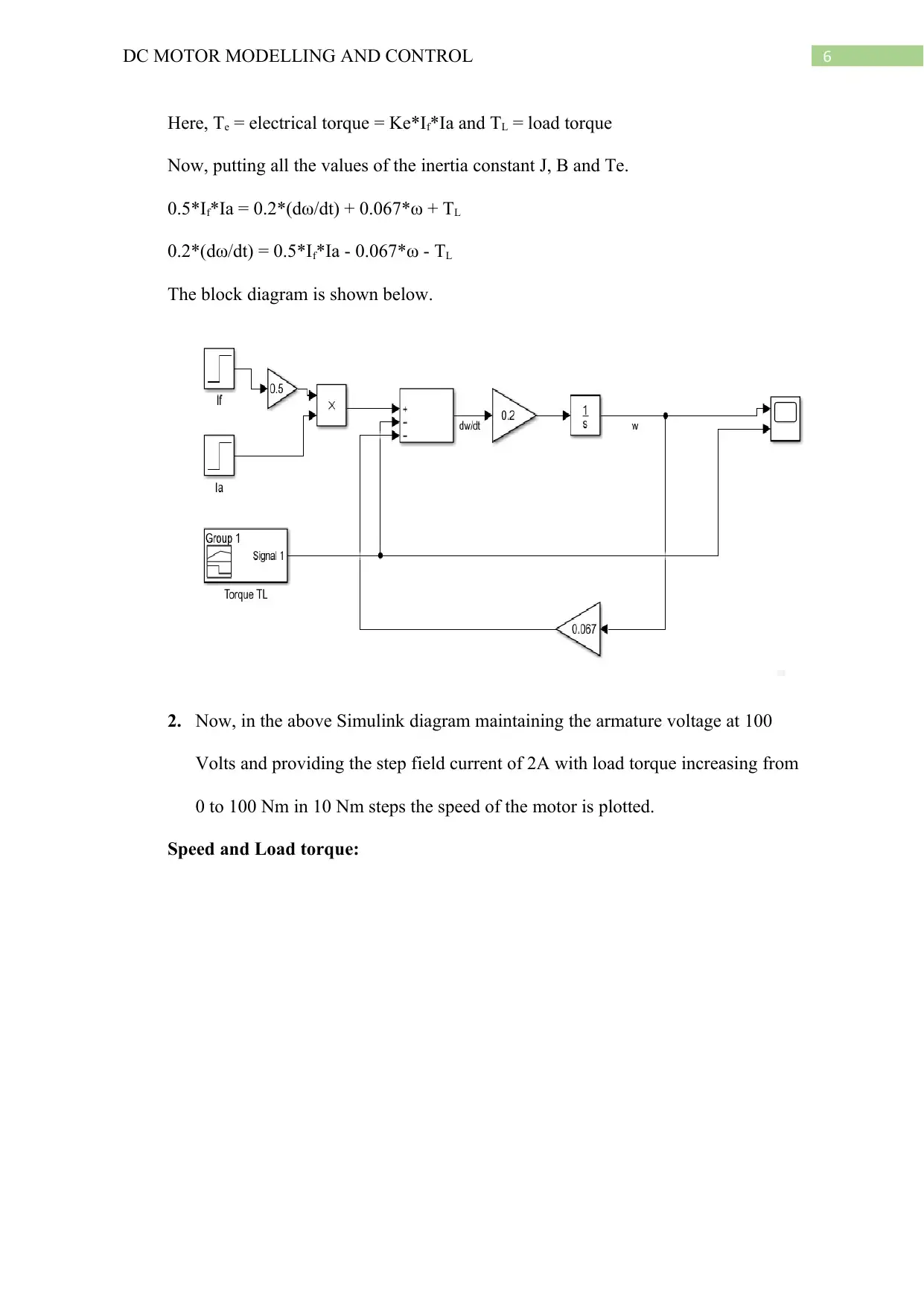
Here, Te = electrical torque = Ke*If*Ia and TL = load torque
Now, putting all the values of the inertia constant J, B and Te.
0.5*If*Ia = 0.2*(dω/dt) + 0.067*ω + TL
0.2*(dω/dt) = 0.5*If*Ia - 0.067*ω - TL
The block diagram is shown below.
2. Now, in the above Simulink diagram maintaining the armature voltage at 100
Volts and providing the step field current of 2A with load torque increasing from
0 to 100 Nm in 10 Nm steps the speed of the motor is plotted.
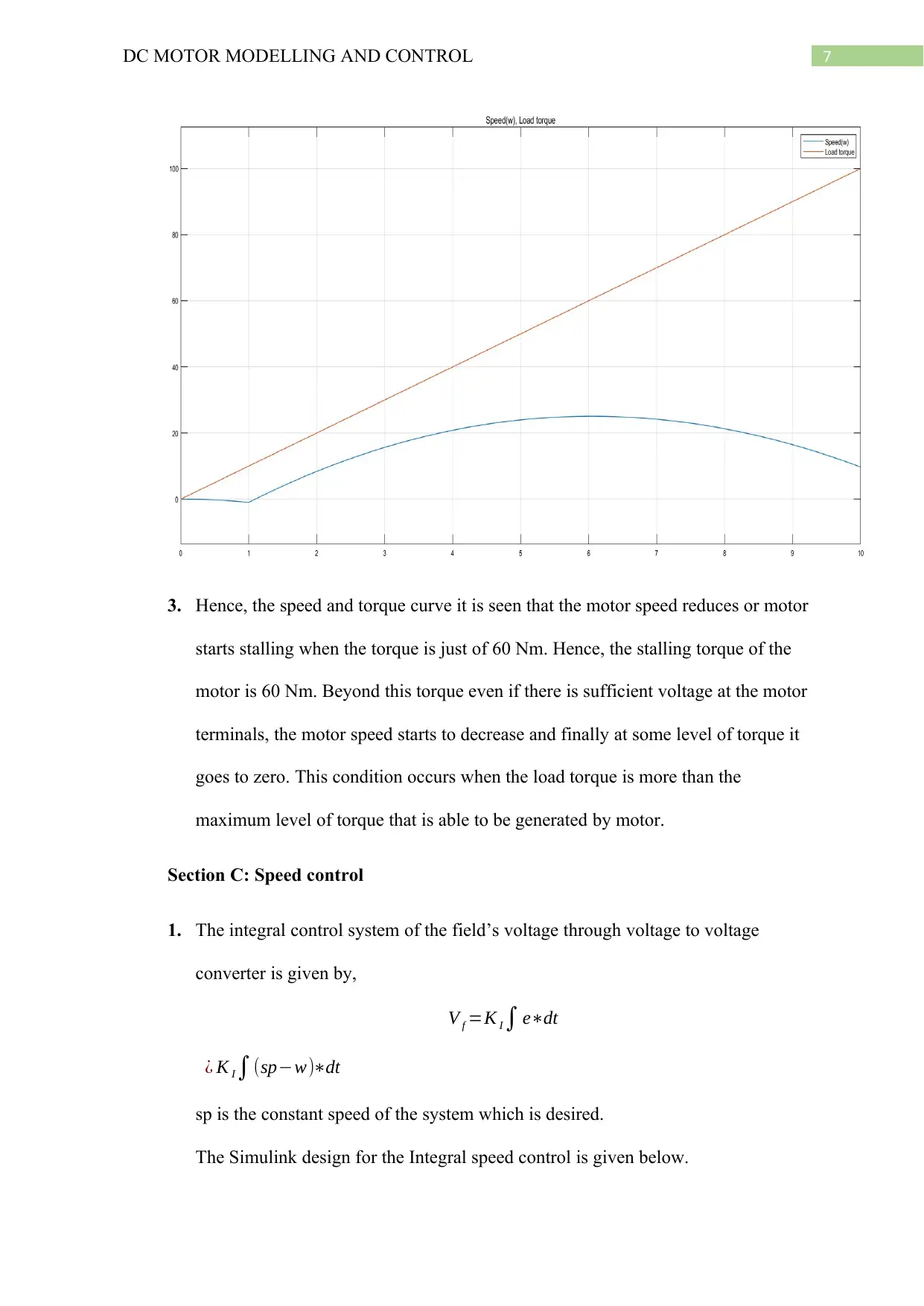
Speed and Load torque:

7DC MOTOR MODELLING AND CONTROL
3. Hence, the speed and torque curve it is seen that the motor speed reduces or motor
starts stalling when the torque is just of 60 Nm. Hence, the stalling torque of the
motor is 60 Nm. Beyond this torque even if there is sufficient voltage at the motor
terminals, the motor speed starts to decrease and finally at some level of torque it
goes to zero. This condition occurs when the load torque is more than the
maximum level of torque that is able to be generated by motor.
Section C: Speed control
1. The integral control system of the field’s voltage through voltage to voltage
converter is given by,
V f =K I∫ e∗dt
¿ K I∫(sp−w)∗dt
sp is the constant speed of the system which is desired.
The Simulink design for the Integral speed control is given below.

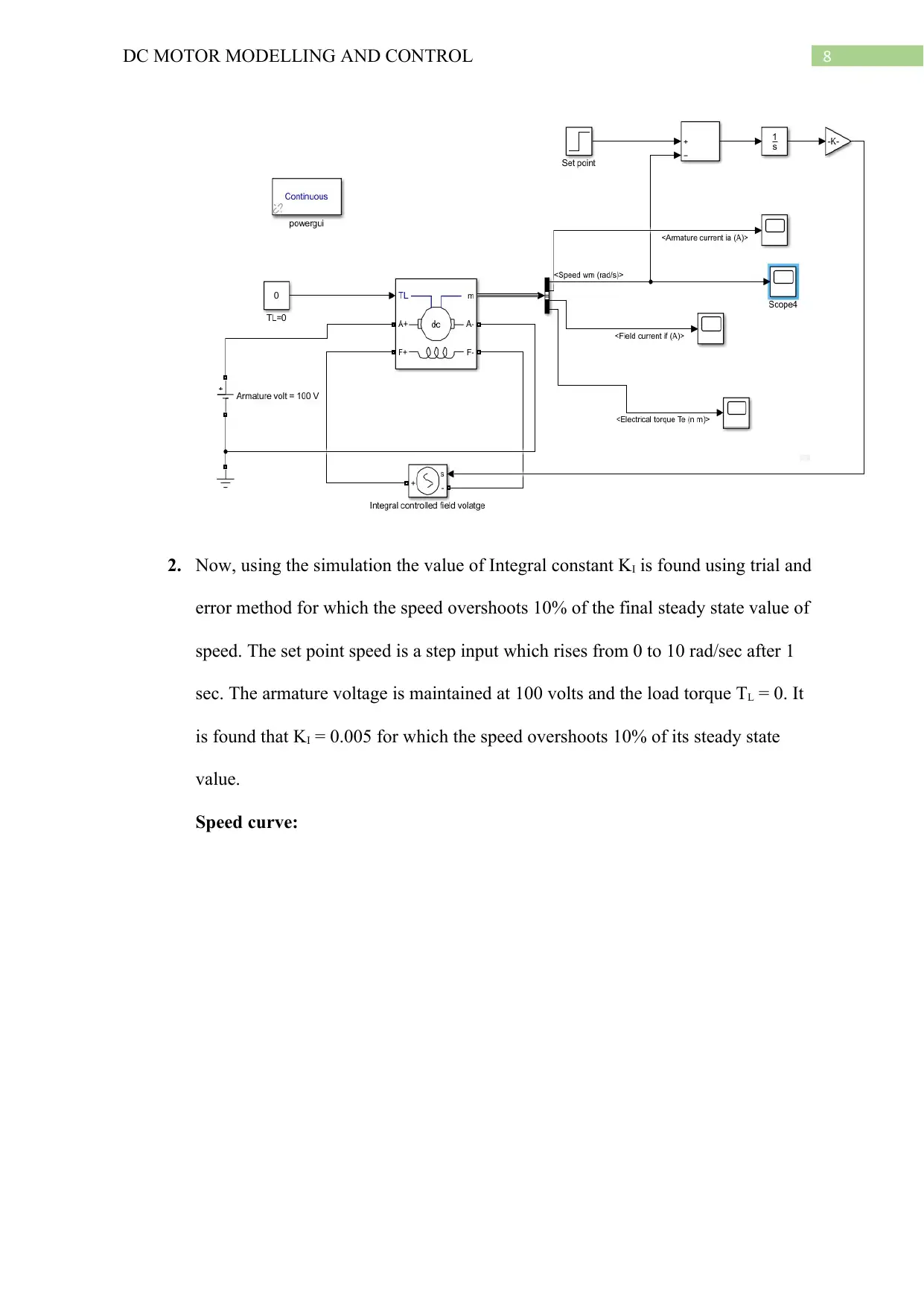
8DC MOTOR MODELLING AND CONTROL
2. Now, using the simulation the value of Integral constant KI is found using trial and
error method for which the speed overshoots 10% of the final steady state value of
speed. The set point speed is a step input which rises from 0 to 10 rad/sec after 1
sec. The armature voltage is maintained at 100 volts and the load torque TL = 0. It
is found that KI = 0.005 for which the speed overshoots 10% of its steady state
value.
Speed curve:

9DC MOTOR MODELLING AND CONTROL
Hence, it is seen from the above speed curve of motor that for the particular value
of KI given above the speed at about 18 secs become 11 rad/sec which is 10%
more that the steady state speed which is 10 rad/secs.
3. Now, the set point is changed from 20 to 30 rad/sec and the same method is
applied and for same KI = 0.005 for which the speed overshoots 10% of its final
steady state value. The overshoot speed value and final steady state speed is
observed. The set point step input is specified in the Simulink step block as given
below.

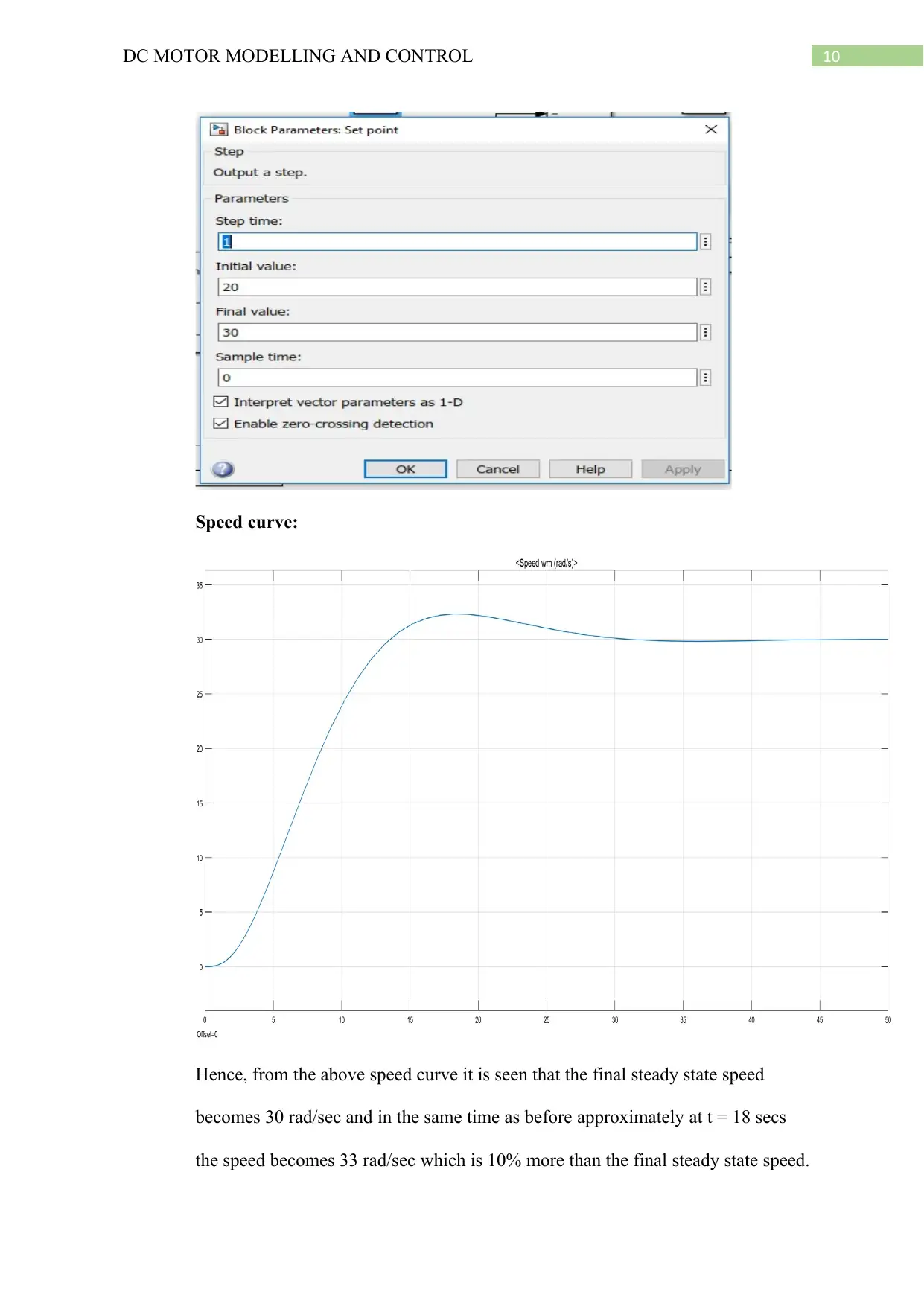
10DC MOTOR MODELLING AND CONTROL
Speed curve:
Hence, from the above speed curve it is seen that the final steady state speed
becomes 30 rad/sec and in the same time as before approximately at t = 18 secs
the speed becomes 33 rad/sec which is 10% more than the final steady state speed.

11DC MOTOR MODELLING AND CONTROL