Design of a Transmission System with Parametric CAD Implementation

This document provides a complete system design calculations for a transmission system with parametric CAD implementation. It includes identification of parts, calculation of power, selection of a grooved pulley, design of shaft, fatigue analysis, and more. The document also discusses CAD implementation with 3D CAD models and 2D drawings.

Design of a Transmission System with Parametric CAD Implementation
[Document subtitle]
[DATE]
[Company name]
[Company address]

Contents
Section A: Complete System Design Calculations..........................................................................3
A. Identification of Parts:.............................................................................................................3
B. Calculation of power:..............................................................................................................6
C. Selection of a Grooved pulley to replace existing Flat pulley:.............................................11
D. Selection of V belt system to replace the Existing Flat belt pulley AB:...............................16
E. Design of Shaft:.....................................................................................................................22
F. Fatigue Analysis of shaft.......................................................................................................32
G. Design of shaft deflection:....................................................................................................38
h. Keys and Keyways selection:................................................................................................41
I. Selection of bearing:...........................................................................................................43
Section B: CAD implementation:..................................................................................................46
1. 3D CAD models:....................................................................................................................46
1.1 Complete Assembly:........................................................................................................46
Parts............................................................................................................................................47
2. 2D Drawings..........................................................................................................................51
Section C:.......................................................................................................................................57
Discussion and Recommendations:...............................................................................................57
Conclusion:....................................................................................................................................57
References......................................................................................................................................58
Appendix A:...................................................................................................................................59
Appendix B:...................................................................................................................................61

Section A: Complete System Design Calculations
A. Identification of Parts:
In this topic the various parts associated with the system which was examined will be explained
briefly with their operations. The schematic layout of the given system is given at the figure1.
The various parts of the system will be initially identified and then explained briefly.
Figure1. Image illustrates the schematic of the given system.
The various parts present in the system are:
1. A Shaft of 850mm Length.
2. Pulley AB of 250 mm diameter.
3. Pulley CD of 300 mm Diameter.
4. Assembly of two Bearings with housing at the both ends.
5. Keyways
6. Screws.
Part1: Shaft:
The Major part of the system is the shaft. A shaft is a rotating machine element which is used to
transmit motion, torque and power. The shafts are of circular cross section in general. The shaft
plays a key role in power transmission such as gearbox, propeller shaft, wheel axle shafts, etc.
The shafts should be designed for reliability, strength and life. It should have good load bearing
capacity and also the vibrational characteristics must be considered. The shaft designed should

be targeted for low mass and high strength. Material for the shafts are generally low carbon steel,
hot rolled steel, cold drawn steel, etc. (Whitman, M.P. 2015)
Part2: Pulleys
The system consists of two pulleys one of diameter 250 mm and another pulley of 300mm
diameter which are used to receive and transmit power from the source to the final system. One
of the pulley among them is driving pulley another one is driven. A pulley is a mechanical
structure which consists of a wheel attached to a shaft, it is rotated by a belt assembly which is
mounted at the top of the pulley wheel. There are many types of pulleys such as Flat belt pulley,
V-groove pulley, double V-groove pulley, etc. The pulleys are to be selected on the basis of the
power transmission requirements, torque loads acting, type of applications and the reliability
requirements of the system. (Antchak, J.R., et.al 2018)
Part3: Bearings with housing:
A bearing is a machine part which act as a support to the parts in motion and also helps to
confine the motion of the part. The bearing is utilized in almost all machine parts such as
automobiles, pumps, generators, turbines, etc. The bearings are selected on the basis of the
design of the shaft and the service factor requirements. The bearings are of different types. They
can be classified as follows:
1. Radial bearings
2. Thrust bearings
1. Radial bearings:
Figure2. Image illustrates the various parts of a radial bearing assembly.

The radial bearings are also called as sliding contact bearings, they can be used in the application
where the loads are acting along the circumferential direction along the bearings. The figure2
illustrates a typical radial bearing.
They are further classified into four types as:
a) Zero film bearing.
b) Thin film.
c) Thick film.
d) Externally pressurized.
2. Thrust bearings:
Thrust bearings are used in places where axial thrust force acts on the bearing such as office
chairs and other machine components.
Figure3. Illustrates the thrust bearing exploded view.
Bearings are mounted on a supporting house which is used to confine the bearing and the shaft
attached to the bearing. The whole assembly is bolted or attached to a foundation.

Figure4. Image illustrates a typical bearing confined on a housing.
B. Calculation of power:
Power to be transmitted:
The layout diagram of the existing system si provided the data available from the given system
are the geometric properties of the shaft, pulleys, the distance between two pulleys, etc. The
power transmitted is not provided, so the power transmitted by the exsiting system will be
calculated. Then the power flow required by the system to be redesigned will be calculated by
finding the value of the power that is 15 times greater than that of the calculated power of the
existing system. As the power requirement is given as 15 times the proposed system. (Gonen, T.,
2015)
Power transmitted by the existing system:
The power is given by the equation:
P = 2 πNT/ 60 in Watts
Where,
N is the speed in RPM

T is the Toque
Now,
The toque of the existing system can be calculated as:
Torque, T = π
16 ƫ d3
Where,
ƫ is the shear stress in N/m2
d is the diameter of the shaft in m.
T is the toque in N.m
The power of the existing system can be calculated by finding the power transmitted by the
pulley on the existing system as the pulley is mounted on the shaft only.
The power transmitted by the Pulley CD can be calculated as:
P = (T𝛚)
Where,
P is the power transmitted.
T is the Torque transmitted.
𝛚 is the Angular acceleration.
The torque T can be calculated using the relation between the forces acting
on the tight and slack side of the pulley. The forces are acting on the side F1
and F2 for the existing system is given as:
T = (F1-F2) r
Where,
F1 is the Force acting on the tight side.
F2 is the force acting on the slack side.
r is the radius of the pulley.

From the diagram provided in the Appendix A the force transmitted F1 and F2 are taken as:
Force on tight side, F1: 270 N
Force on slack side, F2: 50 N
Radius: r: 0.15 m
Now,
T = (270-50)(0.15)
T = 33 N.m = 24.339 Ft-Ib
The total amount of power transmitted by the pulley CD is:
From the technical specifications the angular velocity of the Shaft: 1500 Rpm: 157 Rad/sec
P = 33(157) = 5181 W = 5.181 KW
P = 7.0441996 PS
The power transmitted by the pulley CD is found as 7.0441996 PS.
The forces acting on the P1 and P2 sides of the Pulley AB when considering the frictional
losses of 10 percent. Can be calculated as follows:
Considering 7.0441996 PS of Power is transmitted from the Pulley CD of diameter 300 mm.
Power loss due to friction: 10 percent
Shaft rotation: 157 Rad/sec
Angle of the pulley: 2A = 450
Diameter of pulley CD: 300 mm
Diameter of the pulley AB: 250 mm
Radial difference between the diameters of the pulleys
Power transmitted by the Pulley AB = (7.0441996) (0.9) [Considering 10 percentage
power loss]
Power, P = 6.34 Ps

Now,
P = (T𝛚)
Where,
P is the power transmitted.
T is the Torque transmitted.
𝛚 is the Angular acceleration.
4.66 = T (157)
Torque, T = 4662/157 = 29.7 N.m = 21.90 Ft-Ibs
The torque transmitted by the pulley AB is found as 21.90 Ft-Ibs.
Now,
T = (P1−¿P2) r
(P1−¿P2) = T/r
(P1−¿P2) = 29.7/ 0.125 = 237.6 N.m
Now,
P1 / P2 = [e^(μθ)] / Sin (A)
Where,
P1 and P2 are the forces acting on tight and slack sides.
θ - Angle of wrap on P1 is calculated as:
θ= 180 - 2A = 180- 45 = 1350 = 2.356 Rad/s
μ Coefficient of friction: 0.4 (Assumed)
We have,
(P1−¿P2) = 237.6 N.m
P1 = 237.6 +¿ P2 N.m
Now,

P 1
P 2 =eμθ ¿ ¿
sin A =6.705
P2 = (P1) / 6.705
P2 = (237.6 +¿P2) / 6.705
6.705 P2 = 237.6 + P2
6.705 P2 –P2 = 237.6
5.705 P2 = 237.6
P2 = 41.6476 N
Substituting the value of P2 in equation (P1−¿P2) = 237.6 N.m
We get,
P1 = 279.24 N (or) 28.47 Kgf
The force P1 is calculated as 279.24 N (or) 28.47 KgF
The force P2 is calculated as 41.676 N (or) 4.249 KgF
Flow chart1. Illustrates the power flow diagram.
Motor Pulley
CD Pulley
AB Output
10% Power
loss

C. Selection of a Grooved pulley to replace existing Flat pulley:
Now the grooved pulley which will replace the existing 300 mm diameter flat belt pulley will be
selected.
The pulley will be selected based on the power transmission criteria of the shaft. The new system
design should be designed to carry 15 times more power than that of the existing system. The
Power transmission requirements of the pulley are calculated as (Tsukamoto, M et.al 2015):
Power required to transmitted by the pulley:
P=15 X ( Power transmitted by pulley CD)
PCD = 7.044 PS
P = 15 X (7.044)
P = 105.66 PS
The flat belt pulley CD is of 300 mm diameter. The power transmitted by the pulley is found as
105.66 PS
The Selection procedure to be followed for choosing a V belt drive system is as follows
(Dalsania, B.,et.al 2015):
Step1: Determine the Design power
a) Calculate service factor
b) Find design power
Step2: Select type of belt
Step3: Select belt cross section
Step4: Select pulley diameter
Step5: Selection of center distance
Step6: Belt length determination
Step1: The design power. The system need to transmit 15 times of the power transmitted by the
existing system. The design power is calculated by multiplying the rated power with service
factor. The service factor table is given below:

The system is about to run 16 hours per day. The service factor is taken as 1.2 and the system is
designed to withstand 15X higher power than the existing system (Pawar, A.R., et.al 2016).
Design power: (105.66) X 1.2 = 126.7 PS (or) 94 KW
Step2: From the table the Type of belt required is selected based on the power and the Rpm.
The minimum belt diameter required for the V groove belt can be found with the help of the
table given below:
Power: 94KW
Rpm: 1500

Table2. Belt type selection table
From the power and the Rpm requirements the belt type is selected as SPB
Step3. Select belt cross section:
The belt cross section is selected with the help of the table given below:

Table3. Belt cross section selection table
The cross section that is suitable for the power 83.88 KW and the speed 1500 rpm is chosen as B
Now the cross section dimension details can be taken from the data table4. The selected cross
section of the belt is SPB:

Table4. Cross section of belt (Dimensional data)
The selected cross sectional details are tabulated as:
Cross
section
Pulley
Groove
datum
width
Min
distance
from
outside
diameter
to datum
diameter
Min
groove
depth
from
datum
Center to
center
distance
of grooce
Edge of
pulley to
first
groove
center
Groove
angle
Min. Top
width
SPB
B
14 3.50 14 19.0 12.5 34-38 16.10-
16.40
Step4 : From the table the required power is 94 KW (or) 126.7 Ps and the Rpm is 1500, the
minimum diameter of the pulley required is selected from the table5. as: : 224 mm (or) 8.82 in
The diameter of the Pulley is 212mm or 8.82 in.
Now as per the available BSi standards the Pulley diameter is chosen as 9.25 in.

Table5. Pulley diameter
Step4: Pulley selection is tabulated as:
No. of Grooves Pulley OD Pulley bore
Diameter
Material Weight Kg
1 9.25 in 7/8 in Cast Iron 2.18
D. Selection of V belt system to replace the Existing Flat belt pulley AB:
The flat belt pulley AB is of 250 mm diameter. The power transmitted by the pulley is found as
6.34 PS or 4.66 KW. (Silva, C.A., et.al 2018)
Similar to that of the previous selection procedure the belt will be selected.
The Selection procedure to be followed for choosing a V belt drive system is as follows:
Step1: Determine the Design power
c) Calculate service factor
d) Find design power
Step2: Select type of belt
Step3: Select belt cross section
Step4: Select pulley diameter
Step5: Selection of center distance
Step6: Belt length determination

Step1: The design power. The system need to transmit 15 times of the power transmitted by the
existing system. The design power is calculated by multiplying the rated power with service
factor. The service factor table is given below:
Table1.
Now,
The system is about to run 16 hours per day. The service factor is taken as 1.2 and the system is
designed to withstand 15X higher power than the existing system
Design power: 15 X (4.66) X 1.2 = 83.88 KW (or) 114 PS
Step2: From the table the Type of belt required is selected based on the power and the Rpm.
The minimum belt diameter required for the V groove belt can be found with the help of the
table given below:
Power: 83.88

Rpm: 1500
Table2. Belt type selection table
From the power and the Rpm requirements the belt type is selected as SPB
Step3. Select belt cross section:
The belt cross section is selected with the help of the table given below:

Table3. Belt cross section selection table
The cross section that is suitable for the power 83.88 KW and the speed 1500 rpm is chosen as B
Now the cross section dimension details can be taken from the data table4. The selected cross
section of the belt is SPB:

Table4. Cross section of belt (Dimensional data)
The selected cross sectional details are tabulated as:
Cross
section
Pulley
Groove
datum
width
Min
distance
from
outside
diameter
to datum
diameter
Min
groove
depth
from
datum
Center to
center
distance
of grooce
Edge of
pulley to
first
groove
center
Groove
angle
Min. Top
width
SPB
B
14 3.50 14 19.0 12.5 34-38 16.10-
16.40
Step4: From the table the required power is 83.33 KW (or) 114 Ps and the Rpm is 1500, the
minimum diameter of the pulley required is selected from the table5. as: : 212 mm (or) 8.34 in
The diameter of the Pulley is 212mm or 8.34 in.
Now as per the available BS standards the Pulley diameter is chosen as 8.25 in.

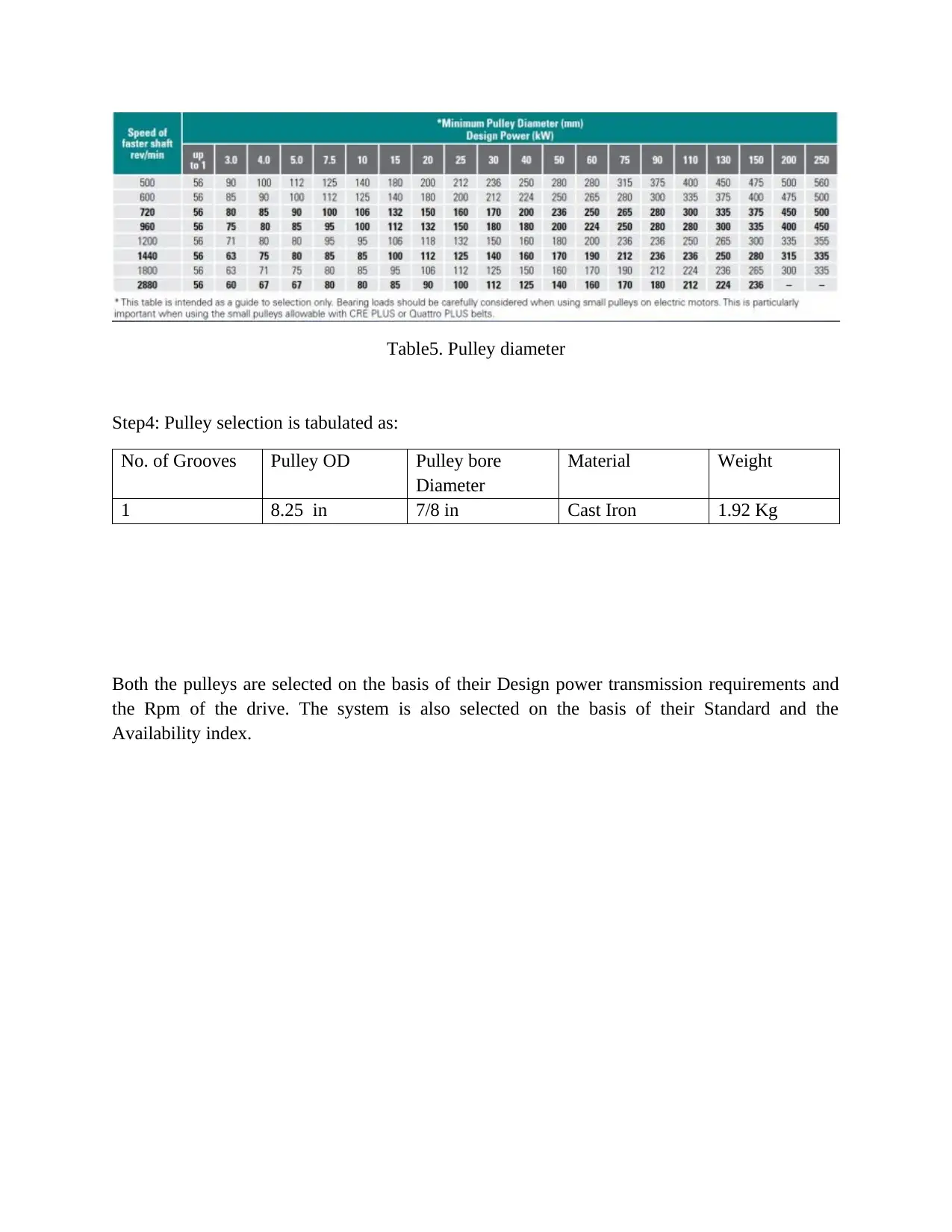
Table5. Pulley diameter
Step4: Pulley selection is tabulated as:
No. of Grooves Pulley OD Pulley bore
Diameter
Material Weight
1 8.25 in 7/8 in Cast Iron 1.92 Kg
Both the pulleys are selected on the basis of their Design power transmission requirements and
the Rpm of the drive. The system is also selected on the basis of their Standard and the
Availability index.

E. Design of Shaft:
The shaft design is carried out in order to meet up with the power transmission requirement
criteria of the selected pulleys.( Sankar, V., 2018)
Now a shaft is needed to be designed for the purpose of transmitting a rated power of 77.715
KW, as the power to be transmitted by the new shaft is 15 times greater than that of the existing
system. The maximum power transmitted is constant throughout the shaft. The shaft should be
designed for strength (Kim, B. et.al 2016)
Now we have the following details:
Power transmitted: 77.715 KW
The diagram of the shaft and the pulley system selected are drawn as:
Figure5. Sketch of the shaft and pulley assembly and the forces acting on pulley.

The self-weight of the pulley AB is taken as 1.93 Kg and the Pulley CD is taken as 2.2 Kg
from the manufacturer website. The self-weight of the Shaft is assumed to be 2.4 Kg
The force acting on the pulley CD (Kate-Deshmukh, N.S., et.al 2018):
Now,
F1 = (50+270) = 320 N + 24 N + 22 N = 366 N
Force acting on the pulley AB:
The force acting on the pulley AB is resolved into two
components Horizontal and Vertical.
F2 = 280+42 = 322N +24N + 19.3 N = 365.3 N
F2horizontal = F2 Cos θ = 322 (Cos 45) = 258.3 N
F2vertical = F2 sin θ = 322 Sin 45 = 258.3 N
Calculation of reaction forces for Horizontal component:
The Free body diagram for the forces acting on horizontal direction is shown as:
Figure5. Shows the Horizontal force components of the shaft.

The reaction forces acting on the beam is calculated by:
We know that,
RO + RE = Sum of all the forces.
RO + RE = 366-258.3 = 107.7 N
Now taking Moment about O
RE ¿ (−P 1∗300+ P 2∗700)/850
RE ¿ (−258.3∗300+366∗700)/850=210.25 N
Now,
RO = 107.7 −¿RE
RO = −¿102.6 N
The calculated forces at the supports for the horizontal plane is:
RO = −102.6 N
RE ¿ 210.25 N N
Shear force acting on the horizontal plane:
SF at O = −102.6 N
SF at AB = S.F at O +¿ 227 = -102.6 + 258.3 = 155.75 N
S.F at CD = S.F at AB +¿ (-366) = -210.30 N
S.F at E = -210.30 N
Horizontal Bending Moment calculation:

BM at O = 0
B.M Hor at AB = (-102.6) (300) = -30.770 KN. mm
B.M Hor at CD = (-102.6 )(700) + (227)(400) = 31.550 KN.mm
B.M Hor at E = 0
The Shear Force and Bending moment diagram is drawn as:
Figure6. Shear Force and Bending Moment Diagram for Horizontal plane.
Now,

S.F and B.M calculation for the Vertical plane:
The Free Body diagram is given:
Figure7. Shows the Free Body Diagram of the Forces acting on Vertical plane.
.
Calculation of reaction forces for Vertical component:
The reaction forces acting on the beam is calculated by (Krause, W.R., et.al 2018):
We know that,
RO + RE = Sum of all the forces.
RO + RE = -258.3 N
Now taking Moment about O

RE ¿ (−P 1∗300)/850
RE ¿ (−¿ 258.3*300 ) / 850¿−91.16 N
Now,
RO = -258.3+91.16 = −167.14N
RO = -167.14 N
The calculated forces at the supports for the horizontal plane is:
RO = −167.14 N
RE ¿ −91.16 N
Shear force acting on the Vertical plane:
SF at O = −167.14 N
SF at AB = S . F at O+227=−167.14+258.30=91.16 N
S.F at E = 91.16 N
Vertical Bending Moment calculation:
BM at O = 0
B.MVer at AB = (−167.15)(300) = −50.140KN. mm
B.M at E = 0
.
The Shear Force and the Bending Moment diagram for the vertical plane is drawn as:

Figure8. Shear Force and Bending Moment Diagram for Vertical plane.
The Resultant Shear stress is calculated as (Shaikh, S.M., et.al 2018):
Resultant Shear Force = √SFhor2 +SFver2

Point Shear Force Vertical Shear Force
Horizontal
Resultant Shear
Force
O −102.6 N −167.14 N 195.80 N
AB 155.75 N 91.16 N 180.46 N
CD 210.30 N 0 210.30 N
E -210.30 N 91.16 N 228.9 N
The maximum amount of force acts at E which is calculated as 228.9 N
The Resultant Bending Moment calculations:
Resultant Bending Moment = √ MBhor2+ MBVer2
Bending Moment at O = 0
B.M at AB = 58.8 KN.mm
Bending Moment at CD = 31.550 KN.mm
Bending Moment at E = 0
Point Bending Moment Vertical Bending Moment
Horizontal
Resultant Bending
Moment
O 0 0 0
AB −30.770 KN . mm −50.140 KN . mm 58.850 KN . mm
CD 31.550 KN . mm 0 31.550 KN . mm
E 0 0 0
From the calculations it is found that the Bending Moment is Maximum at the point AB,
which is equal to 58.8 N.m (or) 43.36 lbf.ft
Now,

The maximum shear stress theory is applied to find the minimum diameter. Also the design
safety will also be checked with the shear stress that is found. The obtained shear stress
should be lower than that of the Maximum allowable shear stress of the material.
The chosen material is Alloy steel with composition 37 Mn 2 Mo 28
Yield Strength, σ y of the material: 60 Kgf/mm2
Shear stress = σ y
2( FOS) Kgf/mm2
FOS is the Factor of Safety which is taken as: 1.5
Now applying and calculating,
Shear Stress = 20 Kgf/mm2 = 19.610 e7 N/m2 = 196 Mpa
The Maximum Shear Stress, ƫmax = 16
π d3 T eq ¿ 10 Kgf/mm2
Here,
Teq = √ M 2+T 2
where,
M is the Maximum bending moment: 58.8 N.m
T is the Torque
d is the diameter
P= 2 πNT
60
T = 60 P
2 πN = 60 (77.715)
2(3.14)(1500) =0.4947 KN . m
Torque, T = 494.7 N.m

Teq = √58.82 +494.72 = 498.18 N.m
ƫmax = 16
π d3 (498.18)
d3 = 16 /(3.14)(19.61 e 7)(498.18)
d = 0.029 m
Minimum required diameter is 0.02348 m
Check for Safety:
The induced shear stress will be found using applying the maximum force applied on the shaft on
the Maximum principle stress equation and comparing it with the allowable stress (Farouki, R.T.
Linke, B.S., 2016).
Induced stress:
ƫ = 16
π d3 T eq
Here,
Teq = √ M 2( Fd
8 )+T2
where,
M is the Maximum bending moment
T is the Torque
d is the diameter
F is the maximum shear force.
F is taken from the Resultant shear force tabulation laid in the previous section and the calculated
value is obtained as 228.9 N

Now,
Teq = √ (M + ( Fd
8 ) )
2
+T 2 = √(58.8+( 228.9 ( 0.023 )
8 ))
2
+ 494.72
Teq = 58.802
ƫ = 16
π d3 T eq=¿13.020 e6 N/m2 < ƫmax (19.6e7 N/m2)
Now it is clear that the induced stress is less than that of the Allowable stress:
i.e. ƫ (13.020 e6 N/m2) < ƫmax (19.6e7 N/m2)
The design is safe.
The minimum diameter required is taken as 23 mm (or) 7/8” in as per the available BS
standards. (Commercially available at:
https://www.amazon.com/Keyed-Shaft-Dia-18-CS/dp/B01LXVKZF7)
F. Fatigue Analysis of shaft
The shaft that we have previously designed is based on static loading conditions which means
that the torque and bending moment induced in the body is considered to be stationary. The
machine elements such as blanking, piercing, punching, etc. are subjected to Fluctuating loading
conditions, there will be some maximum and minimum stress acting on the shaft which will
change frequently, these kind of shafts are to be designed for Fatigue strength. Fatigue is the
weakness caused in a material due to repeated loading over a period of time (Zhu, S.P., et.al
2015).
The fatigue failure can be formulated by using theories of failures such as Soderberg equation,
Goodman equation and Gerber line. The failure theories are implemented on the basis of the
material properties. The Soderberg equation is widely implemented only for the ductile

materials. The Soderberg equation is the most widely used equation for the design of the shaft.
Also the Material that we have chosen for the shaft is Alloy steel which is a ductile material.
Figure9. Illustrates the various theories of failures.
The Soderberg equation is given by the equation:
1
Fs
= σ a
Se
+ σm
S y
= ƫa
Se
+ ƫm
Sy
Where,
Sy is the Yield stress
σ m is the Mean stress
Se Endurance limit
σ a is the Amplitude of the variable stress

Kf Stress concentration factor.
Fs is the Factor of safety
ƫaAmplitude of variable shear stress
Se Endurance limit of shear stress
ƫm Mean shear stress
Sy Yield shear stress
Now, the problem can be formulated as:
The shaft that we have previously designed and analyzed consists of varying Maximum and
minimum loads:
The Shear Stresses can be formulated from the maximum and minimum loads:
From the resultant Shear Force table:
Resultant Shear
Force
195.80 N
180.46 N
210.30 N
228.9 N
The maximum and minimum Forces are 180.46N and 228.9N.
The Minimum Shear Stress = S . F
A =
180.46
π
4 (0.023)2 = 434.345 KN/m2
The maximum Shear stress =
SF
A = 228.96
π
4 (0.023)2 = 550.934 KN/m2
Material Properties:

Material Selected: Alloy steel
σ y, Yield Strength: 600 Mpa
ƫ y Yield Shear Stress: 0.5 σ y = 300 Mpa
Su, Ultimate strength 85 Kgf/mm2 = 850 Mpa
Now,
The Factor of safety will be found using the Soderberg equation:
1
Fs
= ƫa
Se
+ ƫm
Sy
Here,
Fs is the Factor of safety
ƫaAmplitude of variable shear stress
Se Endurance limit of shear stress
ƫm Mean shear stress
Sy Yield shear stress
Now,
We previously found that,
σ y, Yield Strength: 600 Mpa
ƫ y Yield Shear Stress: 0.5 σ y = 300 Mpa
Su, Ultimate strength 85 Kgf/mm2 = 850 Mpa

Se-Endurance Limit Modification Factor:
S e=K a K b K c K d K e K f Se
'
Where,
Ka : Surface condition modification factor
Kb : Factor of size modification.
Kc : Factor of load modification.
Kd: Factor of temperature modification.
Ke: Reliability factor
Kf: Factor of Miscellaneous modification.
S’e : Rotary beam test specimen endurance limit.
Calculation for all the Factors K a K b K c K d K e K f are given in the Appendix B.
The final calculated values are (for detailed calculations See Appendix B):
Ka = 0.755
Kb = 0.88
Kc = 1
Kd = 1
Ke = 0.897
Kf = 1
S’e = 0.5 Sut = 425 Mpa
Now,

S e=K a K b K c K d K e K f Se
'
S e=0.755 X 0.88 X 1 X 1 X 0.897 X 1 X 425
Se = 253.28 Mpa
Mean shear stress:
ƫ m= ƫmax+ ƫmin
2 =492.6 K Pa
Amplitude:
ƫa= ƫmax −ƫmin
2 =550.93−434.3
2 =58.3 Kpa
Now,
Applying all the values in the formula:
1
Fs
= ƫa
Se
+ ƫm
Sy
We know:
Fs : 1.5
ƫa = 0.0583 Mpa
ƫm=0. 492 M Pa
Se = 253.28 Mpa
Now,
The induced Yield shear stress should be less than that of the Allowable Yield shear which is
20MPa.

Now,
0.66666 = 2.3018e-4+ ƫm
S y
Sy = 0.492/0.666436 = 0.738 M Pa
Sy = 0.738 Mpa < Allowable shear stress (20 Mpa)
The Design is safe for Fatigue loading conditions.
G. Design of shaft deflection:
The Maximum Deflection of the system will be found and compared with the Requirements:
The maximum allowable deflection is given as: 1/5000 of its length (Yu, Y., 2017):
1
500 ( 850 ) =1.7 mm
Dallow = 1.7e-3 m
The maximum loading occurs at the horizontal plane so taking the load acting on the horizontal plane:
The free body diagram of the beam with loads are provided as:
Length of the beam: 850mm
Distance from O to AB: 300mm
Distance from AB to CD: 400mm

Distance from CD to E: 150mm
Moment of inertia of the cross section: I = π
64 0.0234=1.37966 e-8 m4
To find the maximum deflection:
Reactions at RO and RE are previously calculated as:
RO = −102.6 N
RE ¿ 210.25 N N
Now consider a section X at the last portion of the beam from CD to Point E at a distance x from the left
side.
The B.M at this point is given by:
EI d2 y
dx2 = RO x | +258( x−0.3) | −366( x−0.7)
= -102.6 x | +258( x−0.3) | −366( x−0.7) …………….i
Integrating the equation we get:
EI dy/dx = -102 x2
2 + C1 ¿+258 ( x−0.3)2
2 | -366 ( x−0.7)2
2
= -51x2 + C1 | 129 ( x−0.3)2 | -183 (x−0.7)2 …………ii
Integrating the equation third:
EI y = -17 x3 + C1 x + C2 | 43 ( x−0.3)3 | -61 (x−0.7)3 …………iii
Now,
To find the values of the C1 and C2 we need to apply the boundary conditions:
(i) At x=0 y=0
(ii) At x=0.85 , y=0
Substituting the B.Cs and solving we get:
C2 = 0

C1 = -4.24
Now substitute the values of C1 and C2 in eqn iii we get,
EI y = -17 x3 -4.24 x | 43 (x−0.3)3 | -61 (x−0.7)3 …………iv
For max deflection the value of dy/dx =0.
Equate eqn ii to 0 upto second line.
0=−51 x2−4.24+129 (x−0.3)2
On solving,
0 = 78x2 – 77.4x +111.8
X =0.496 m
Now,
Substitute the value of x in the equation iv upto second line.
EI ymax ¿−17 x3 −4.24 x + 43( x−0.3) 3
Y max = -3.85/ EI = -3.85/(210e9)1.37966 e-8 = 1.3288 e-3 m
The maximum deflection of the material is calculated as 1.3 mm.
Maximum deflection (1.3mm) is < Allowable deflection (1.7 mm)

h. Keys and Keyways selection:
The Keys and the Keyway required for the shaft and the pulley are done as per the British
standards as:
Key experience shearing and crushing. The material for the shaft and the key should be same
(Kalpakjian, S., et.al 2014).
The material for key: Alloy Steel
Composition: 35Mn 2 Mo28
Shaft diameter: 23 mm
Type of key: Rectangular
Geometry definition for the Rectangular key profile is shown as:

Figure9. Geometry definition of keyway
The key and the Keyway are designed on the basis of British Standards (BS 4235-1:1972)
The table for Key and Keyway selection is given below:
Table3. Keyway and Key selection as per BS standards

Selection of Key:
For 23 mm shaft diameter Key cross section 8 X 7 is selected.
b:8 mm
h:7 mm
Keyway:
Shaft depth: 4mm
Hub depth: 3.3 mm
Tolerance: Normal
Shaft: 0
Hub: +0.018 mm.
I. Selection of bearing:
The bearing should be selected for life of at least 12,000 hours.
Life in hours,
Lh = 16666
n ( C
P )P
Here,
P is equivalent bearing load
n frequency of oscilation
C/P Load ratio.
Based on the Lifetime required and the Rpm of the shaft,((From PSG Design Data handbook,
1982, pg.4.6) ( See Appendix A for Load Ratio Table)

The loading ratio is taken as c
P =¿10.60. (Tech, P.S.G, 1982)
Now,
12000 = 16666/1 (10.60) P
P = 0.067
C = 0.067 (10.60)x 10e3 = 720 Kgf
Now,
The bearing will be selected as per the loading as well as the diameter of the shaft.
From PSG design data SKF 23 series: Self Aligning Ball bearings:
C: 720 Kgf
D(diameter of the shaft): 23 mm

SKF Standard bearing chart (Tech, P.S.G., 1986)
Selected bearing:
Bearing number d D r Max. permissible
RPM
Dynamic
capacity, C

SKF 2305 25 62 2 10000 1900 Kgf
Section B: CAD implementation:
1. 3D CAD models:

1.1 Complete Assembly:
Figure. Illustrates the completely assembled component.
Parts
1. Shaft:

Figure12. Illustrates Shaft CAD model.
2. Pulley:

Fig13. Pulley 3D
3. Bearing:

Fig14. Rendered image of Skf2305 bearing.
4. Bearing Housing

2. 2D Drawings
1. Shaft

2. Pulley 8.25 inch:

3. Pulley 9.25:

4. Key:

5. Bearing:

6. Bearing Housing:

Section C:
Discussion and Recommendations:
The overall redesigning process was carried out manually with the aid of design data handbooks.
Initially the V-belt Pulley selection to replace the existing flat belt pulleys were carried out and
the power flow diagram was laid out. The power losses were considered. The selection of the
pulleys should be accurate and the selected power must be equal to or higher than the Design
power. The DP should be calculated initially by considering proper service factors. Then after
the pulley selection, the Design of Shaft was carried out (Garland, N.P., et.al 2017).
The shaft was designed for static and fatigue loads finally the design should be checked if it can
withstand the design loads also the Deflection occurred on the shaft should also be checked if it
complies with the specified range. Finally a standard shaft size is selected which comply with the
BS standards and are commercially available. The selection of bearing was carried out for the
selected shaft size on the basis of availability and the service life requirements.
 Recommendations to improve the accuracy of the results:
 The design power should be calculated properly
 All the service factors and form factors must be included.
 The system must be designed to comply with certain standards.
 The designed system mst withstand a load equal to or greater than the design load.
 The selection process must also be based on the commercial availability of the selected
product.
The second module consists of creation of CAD model and technical drawing for manufacturing.
The creation of parametric model and drafting can be improvised by following these:
 The model must be done in a high spec system.
 The CAD platform should widely adopted and should be made by following certain
standards.
 The created model must be assembled with proper constrains.
 The modeled parts should be drafted with taking account of particular standards.
 The selected standard must be maintained properly.
 The geometry of the figure must be maintained within the limits.
Conclusion:
The Power transmission system is completely redesigned inorder to transmit 15 times greater
power than the existing system. The individual parts of the complete system are designed as per
the standards parts such as Shaft, pulleys, bearings and bearing housing are designed and
selected to suit the power transmission requirements. All the parts were designed on the basis on
British standards and CAD model of the designed parts are created. The created individual parts
are assembled in the assembly window. Then the parts are drafted to generate Technical
drawings. The drawings are created to comply with the BS standards.

References:
Antchak, J.R., Williams, W. and Dell, J.W., Litens Automotive Partnership, (2018). Isolation
pulley with overrunning and vibration damping capabilities. U.S. Patent 9,989,103.
Dalsania, B., Patel, K., Gabani, V., Singhal, A.S. and Dani, V., (2015). DESIGNING AND
MANUFACTURING OF CONTINUOUSLY VARIABLE TRANSMISSION
(CVT). Engineering and Technologies (ICFTET-(2015)), p.77.
Farouki, R.T. and Linke, B.S., (2016). Shigley Hauler—A competitive project illustrating basic
machine design principles. International Journal of Mechanical Engineering Education, 44(4),
pp.284-301.
Garland, N.P., Glithro, R. and Wade, R., (2017). The Challenges Facing Education in
Engineering Drawing Practice.
Gonen, T., (2015). Electrical power transmission system engineering: analysis and design. CRC
press.
Kalpakjian, S., Vijai Sekar, K.S. and Schmid, S.R., (2014). Manufacturing engineering and
technology. Pearson.
Kate-Deshmukh, N.S. and Gaikwad, M.U., (2016). Design, Analysis and Testing of shaft
mounted speed reducer for coil winding machine.
Kim, B. and Jang, G., (2015), June. TuB-2-1 ROBUST SHAFT DESIGN AGAINST SHAFT
DEFORMATION IN HUB PRESS-FITTING AND DISK CLAMPING PROCESS OF A 2.5"
HDD. In Proceedings of JSME-IIP/ASME-ISPS Joint Conference on Micromechatronics for
Information and Precision Equipment: IIP/ISPS joint MIPE 2015 (pp. _TuB-2). The Japan
Society of Mechanical Engineers.
Krause, W.R. and Edwards, G., Krause William R and Edwards Garland, (2018). FLEXIBLE
SHAFT FOR TRANSFER OF ROTARY MOTION. U.S. Patent Application 15/806,071.
Pawar, A.R., Shinde, K.G., Dey, T. and Narkar, K., (2016). Study on High Speed Spin Test of
Hydraulic Dynamometer by Test Rig Facility.
Sankar, V., 2018. ANALYSIS OF AUTOMOTIVE COMPOSITE PROPELLER SHAFT
USING COMPUTER AIDED GRAPHIC DESIGN.
Shaikh, S.M., Pingale, P.V., Pinjari, S.G., Patil, P.R., Shaikh, T.M. and Godase, S.M., 2018.
Design and Analysis of Composite Drive Shaft.
Silva, C.A., Manin, L., Rinaldi, R.G., Remond, D., Besnier, E. and Andrianoely, M.A., (2018).
Modeling of power losses in poly-V belt transmissions: Hysteresis phenomena (enhanced
analysis). Mechanism and Machine Theory, 121, pp.373-397.

Tsukamoto, M. and Inaoka, T., Kanzaki Kokyukoki Manufacturing Co Ltd, (2016). Driving-side
pulley. U.S. Patent 9,228,644.
Whitman, M.P. and Malinouskas, D.T., Covidien LP, (2015). Shaft, eg, for an electro-
mechanical surgical device. U.S. Patent 8,960,519.
Yu, Y., Yang, Z., Han, C. and Liu, H., (2017). Active vibration control of magnetically
suspended wheel using active shaft deflection. IEEE Transactions on Industrial
Electronics, 64(8), pp.6528-6537.
Zhu, S.P., Huang, H.Z., Li, Y., Liu, Y. and Yang, Y., (2015). Probabilistic modeling of damage
accumulation for time-dependent fatigue reliability analysis of railway axle steels. Proceedings
of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 229(1),
pp.23-33.

Appendix A:
1. Material properties:
Material Properties table (Tech. P.S.G, 1986)

s
2. Bearing Load Ratio Selection Table:
Table4: Bearing Load Ratio (C/P) Selection (Tech, PSG, 1986)

Appendix B:
Calculation of K a K b K c K d K e K f values to find Endurance Limit Modification Factor:
Ka : Surface condition modification factor:
Table1: Surface condition factor table
Using th4e formula:
a:
Sut: 850 Mpa
b = -0.265
Ka = 0.755
Kb: Factor of size modification:
Using the formulae:

Now:
D = 23mm
Applying appropriate formulae:
Kb = 1.24 d^-0.107 = 0.88
Kc: Factor of load modification:
Using the table:
Kc is taken as 1 for bending considering non rotating load.
Kc : 1
Kd: Factor of temperature modification:
The shaft is operated at the temperature of 350 C so the factor of temperature is taken as 1.
Kd = 1
Ke: Reliability factor:
The reliability requirement of the shaft is provided as 90% in the problem description.
Using the reliability factor table given below:

As the reliability is 90percentage,
Ke = 0.897
Kf: Factor of Miscellaneous modification:
No miscellaneous effects are taken into account, Kf = 1