SEO Suggestions for Desklib - Online Library for Study Material

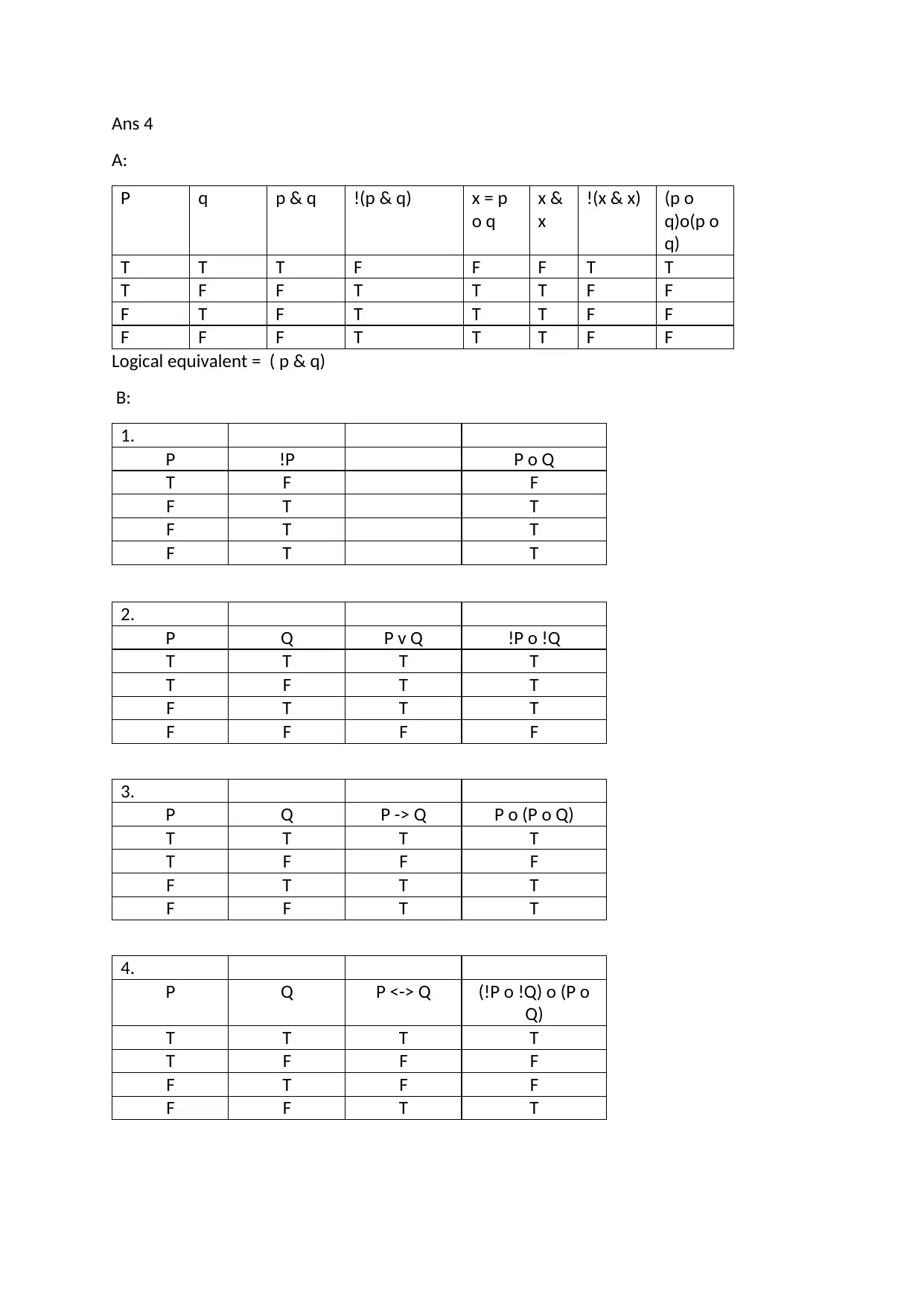
This document provides SEO suggestions for Desklib, an online library for study material. It includes a definition of composition of functions, a graph-based problem, a proof for connected planar graphs, and a truth table for logical operators. It also suggests a title, meta title, and meta description for Desklib's website.

Ans 1:
A:
If Two functions f:S→T and g:T→U can be composed to give a composition gof. This
is a function from A to C defined by (gof)(x)=g(f(x))=f;g
This is known as composition of functions.
B:
R is transitive.
R;R := {(a, a) : There exists a ∈ T such that (a, a) ∈ R and (a, a) ∈ R}
this means R;R = R
R U (R;R) = R U R = R
C:
Given Ri = Ri+1.
R(i-1) U (R(i-1);R) = Ri U (Ri;R) If I keep j=i+1 then Ri =Rj similarly for all j>=i.
D:
Given Ri = Ri+1.
R(i-1) U (R(i-1);R) = Ri U (Ri;R) If I keep k=0 then Rk ⊆ Rj similarly for all k>=0.
E:
By (c) we can say that if (a,b) ∈ Rn+1 and take j=n+1 and i=n then Ri =Rj j>=i.
Hence hint is verified which implies Rn=Rn+1.
F:
R*=Rn = Rn-1 U (Rn-1;R)
If (a,b) is in R* and (b,c) is also in R* => (a,c) is in R*
Hence R* is transitive.

Ans 2:
Potions Charms Herbology Astronomy Transfiguration
Harry Ron Harry Hermione Hermione
Ron Luna George Neville Fred
Malfoy Ginny Neville Seamus Luna
A:
We can formulate this in graph base problem as taking Vertices as student name and
edges as exam name.
Here Different colour edges represent different exam and each vertice represent
different student.
B:
Minimum no of slots cannot be 1 as one student have more than one exam.
If we keep Potions and Transfiguration exam in one slot, Charms and Herbology in
one slot and Astronomy in third then it will minimum number of time slot required
that is 3.
C:
If we have to maximize the number of subjects that can be examined in one time slot
then answer of B will remain unchanged as minimizing time slot also means
maximizing subject.

Ans 3:
A:
Observe the image given below
It has total four faces. Fourth one is the one which is outer region of this graph. So if
graph has only 1 face then they will be like
And for graph with n vertices there will be (n-1) edges.
B:
Relation between planar graph edges(m), vertices(n) and faces(f) is
n-m+f=2
For 1st graph
n= 4, m=6, f=4
4-6+4=2 Hence proved
For 2nd graph
n=8, m =12, f=6
8-12+6=2 Hence Proved

C:
I will proof it by taking induction on m
Base case: m=0
Then G=K1
 n=1, m=0 and f=1
 n-m+f=1-0+1=2
 It is satisfied
Induction Hypothesis: Suppose theorem is true for all connected planar graph with
less than m edges where m>=1
 If G is tree
Then m=n-1 and f=1
So n-m+r= n – (n-1) + 1 =2
It is satisfied
 If G is not a tree then G has a cycle C
Let e be edges of C
Then e is not a bridge as e is only bridge edge when it is not a cycle
If we remove e. G(e-) has n vertices, m-1 edges, f-1 faces
By induction hypothesis theorem hold for G(e-)
Thatmeans n-(m-1)+f-1=2
It is satisfied
Hence n-m+f=2 for connected planar graph.

Ans 4
A:
P q p & q !(p & q) x = p
o q
x &
x
!(x & x) (p o
q)o(p o
q)
T T T F F F T T
T F F T T T F F
F T F T T T F F
F F F T T T F F
Logical equivalent = ( p & q)
B:
1.
P !P P o Q
T F F
F T T
F T T
F T T
2.
P Q P v Q !P o !Q
T T T T
T F T T
F T T T
F F F F
3.
P Q P -> Q P o (P o Q)
T T T T
T F F F
F T T T
F F T T
4.
P Q P <-> Q (!P o !Q) o (P o
Q)
T T T T
T F F F
F T F F
F F T T