Desklib - Online Library for Study Material with Solved Assignments, Essays, Dissertation
VerifiedAdded on 2023/06/10
|11
|2682
|270
AI Summary
Desklib is an online library for study material with solved assignments, essays, dissertation, etc. It offers a vast collection of study material for various subjects and courses including Advanced Diploma of Engineering Technology, MEM23004A, 22228VIC, C6132, MATH7062C, etc.
Contribute Materials
Your contribution can guide someone’s learning journey. Share your
documents today.

STUDENT
STUDENT - KNOWLEDGE ASSESSMENT TASK
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
Student Name)
Student ID
Date
Duration and/or due date 05 August 2018 / week 5
Task instructions
Summary and Purpose of Assessment:
This unit of competency covers the application of mathematical analysis, graphical and software
techniques to engineering problems. It includes exponential and logarithmic functions, trigonometric
equations involving single and double angles, sequences and series, two dimensional vector analysis,
complex numbers, determinants and matrices.
You must demonstrate an understanding of:
Determine scope of technical mathematical techniques required for an engineering application
Apply technical mathematical techniques to engineering application
What and where: This is an individual based classroom assessment.
How: Students will be assessed according to the criteria outlined in the Criteria for Assessment below.
All criteria identified must be addressed to satisfactorily complete this Assessment Task.
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 1 of 11
STUDENT - KNOWLEDGE ASSESSMENT TASK
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
Student Name)
Student ID
Date
Duration and/or due date 05 August 2018 / week 5
Task instructions
Summary and Purpose of Assessment:
This unit of competency covers the application of mathematical analysis, graphical and software
techniques to engineering problems. It includes exponential and logarithmic functions, trigonometric
equations involving single and double angles, sequences and series, two dimensional vector analysis,
complex numbers, determinants and matrices.
You must demonstrate an understanding of:
Determine scope of technical mathematical techniques required for an engineering application
Apply technical mathematical techniques to engineering application
What and where: This is an individual based classroom assessment.
How: Students will be assessed according to the criteria outlined in the Criteria for Assessment below.
All criteria identified must be addressed to satisfactorily complete this Assessment Task.
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 1 of 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

STUDENT
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
1. Late submission approval will be in line with RMIT policy Application for extension of
submittable work (7 calendar days or less) form.
2. Special consideration for assessment Application for special consideration form.
3. Students must submit an electronic copy of this assignment via RMIT CANVAS before its due
date.
4. If a student’s result is NYS: feedback and agreed deadline date for the student to demonstrate
competency will be advised.
5. The date(s) must be within enrolment dates for this competency otherwise the student will be
given a final result of NYS and the student may need to re-enrol/ repeat this course.
This assignment covers PC 1.1, 1.2, 1.3, 2.1, 2.3, 2.4, 2.5 and
PC 1.1, 1.2, 1.3, 2.1, 2.3, 2.4, 2.5
Please Note: Students need to obtain competency (CA) for ALL questions below.
ATTEMPT ALL QUESTIONS
Conditions for assessment
Instructions to Students:
6. All answers are to be written in blue or black pen only, excluding diagrams, or the answers will not
be marked (Written tests only).
7. The ONLY materials, equipment or personal items which may be brought into the test room are
blue or black pens, pencil, eraser and correction fluid (unless otherwise permitted by invigilator)
8. There is to be NO communication of any kind with any other person either inside or outside the
tests venue, except with the test supervisor/invigilator or course teachers.
9. Test papers and other material provided by the University are NOT to be removed from the test
room.
10. You are not permitted to return to the test room, if you leave without permission from the
invigilator.
11. Students found in breach of test conditions can be charged with academic misconduct, have their
results cancelled, be excluded from the program and receive other penalties. Penalties can also
apply if a student’s test material is copied by others.
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 2 of 11
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
1. Late submission approval will be in line with RMIT policy Application for extension of
submittable work (7 calendar days or less) form.
2. Special consideration for assessment Application for special consideration form.
3. Students must submit an electronic copy of this assignment via RMIT CANVAS before its due
date.
4. If a student’s result is NYS: feedback and agreed deadline date for the student to demonstrate
competency will be advised.
5. The date(s) must be within enrolment dates for this competency otherwise the student will be
given a final result of NYS and the student may need to re-enrol/ repeat this course.
This assignment covers PC 1.1, 1.2, 1.3, 2.1, 2.3, 2.4, 2.5 and
PC 1.1, 1.2, 1.3, 2.1, 2.3, 2.4, 2.5
Please Note: Students need to obtain competency (CA) for ALL questions below.
ATTEMPT ALL QUESTIONS
Conditions for assessment
Instructions to Students:
6. All answers are to be written in blue or black pen only, excluding diagrams, or the answers will not
be marked (Written tests only).
7. The ONLY materials, equipment or personal items which may be brought into the test room are
blue or black pens, pencil, eraser and correction fluid (unless otherwise permitted by invigilator)
8. There is to be NO communication of any kind with any other person either inside or outside the
tests venue, except with the test supervisor/invigilator or course teachers.
9. Test papers and other material provided by the University are NOT to be removed from the test
room.
10. You are not permitted to return to the test room, if you leave without permission from the
invigilator.
11. Students found in breach of test conditions can be charged with academic misconduct, have their
results cancelled, be excluded from the program and receive other penalties. Penalties can also
apply if a student’s test material is copied by others.
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 2 of 11

STUDENT
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
12. Plagiarism is the presentation of the work, idea or creation of another person as though it is one’s
own. It is a form of cheating and is a very serious academic offence that may lead to expulsion
from the University. Plagiarised material can be drawn from, and presented in, written, graphic
and visual form, including electronic data, and oral presentations. Plagiarism occurs when the
origin of the material used is not appropriately cited.
13. RMIT special consideration is to enable you to maintain your academic progress despite adverse
circumstances. The process for special consideration can be found at
http://www1.rmit.edu.au/students/specialconsideration
14. Students with a disability or long-term medical or mental health condition can apply for
adjustments to their study and assessment conditions (Reasonable Adjustments and Equitable
Assessment Arrangements) by registering with the Equitable Learning Services (ELS) at
https://www.rmit.edu.au/students/support-and-facilities/student-support/equitable-learning-services
If you already registered with ELS and your study plan is approved, please inform your teacher if
this assessment task is not adjusted in line with approved study plan.
Additional Instructions to Students:
1. Performance requirement:
a. Satisfactory (S) performance ≥ 50% weightage
b. Not Yet Satisfactory (NYS) performance < 50% weightage
Results from this assessment will count towards the final grade only if the result is satisfactory
(S) and will be worth 10% of the final grade.
Equipment/resources students must supply (if
applicable):
Equipment/resources to be provided by RMIT or
the workplace (if applicable):
Computer and RMIT Internet Access
Microsoft Office Suite
Hard copies of the student version of this
assessment task OR access to soft copies
Pens / Pencils
Computer and RMIT Internet Access
Microsoft Office Suite
Hard copies of the student version of this
assessment task OR access to soft copies
Pens / Pencils
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 3 of 11
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
12. Plagiarism is the presentation of the work, idea or creation of another person as though it is one’s
own. It is a form of cheating and is a very serious academic offence that may lead to expulsion
from the University. Plagiarised material can be drawn from, and presented in, written, graphic
and visual form, including electronic data, and oral presentations. Plagiarism occurs when the
origin of the material used is not appropriately cited.
13. RMIT special consideration is to enable you to maintain your academic progress despite adverse
circumstances. The process for special consideration can be found at
http://www1.rmit.edu.au/students/specialconsideration
14. Students with a disability or long-term medical or mental health condition can apply for
adjustments to their study and assessment conditions (Reasonable Adjustments and Equitable
Assessment Arrangements) by registering with the Equitable Learning Services (ELS) at
https://www.rmit.edu.au/students/support-and-facilities/student-support/equitable-learning-services
If you already registered with ELS and your study plan is approved, please inform your teacher if
this assessment task is not adjusted in line with approved study plan.
Additional Instructions to Students:
1. Performance requirement:
a. Satisfactory (S) performance ≥ 50% weightage
b. Not Yet Satisfactory (NYS) performance < 50% weightage
Results from this assessment will count towards the final grade only if the result is satisfactory
(S) and will be worth 10% of the final grade.
Equipment/resources students must supply (if
applicable):
Equipment/resources to be provided by RMIT or
the workplace (if applicable):
Computer and RMIT Internet Access
Microsoft Office Suite
Hard copies of the student version of this
assessment task OR access to soft copies
Pens / Pencils
Computer and RMIT Internet Access
Microsoft Office Suite
Hard copies of the student version of this
assessment task OR access to soft copies
Pens / Pencils
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 3 of 11

STUDENT
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 4 of 11
Task Number 1 of 2 Task Name Assessment 1 – (Part A)
National unit(s) code MEM23004A National unit(s) title Apply technical
mathematics – (Polynomial
Functions Exponential &
Logarithm)
National curriculum code 22228VIC National qualification
title
Advanced Diploma of
Engineering Technology
RMIT Program code C6132 RMIT Course code MATH7062C
Use this version for students to answer the questions, to mark their answers and give feedback to students.
Section A - Assessment Information
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 4 of 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

STUDENT
Section B - Student Answer Sheet
Questions
Provide your responses in the boxes below each question
Q1
:
Given that
then find:
2P(x) -Q(x) + 3R(x)
2 marks
Satisfactor
y
response
Yes
☐
No
☐
A:
P ( x ) =8−3 x +2 x2+ x4
Q ( x )=x5−3 x4−4 x2−1
R ( x )=8 x3+ 7 x2−4 x
Then, evaluate,
2 P ( x )−Q ( x ) +3 R ( x )
Plugging the values
¿ 2 ( 8−3 x +2 x2+ x4 )− ( x5−3 x4 −4 x2−1 ) +3 (8 x3+7 x2−4 x)
¿ ( 16−6 x+ 4 x2 +2 x4 )− ( x5−3 x4 −4 x2−1 ) +(24 x3 +21 x2 −12 x )
¿ 16−6 x+4 x2+ 2 x4 −x5+ 3 x4 +4 x2+ 1+ 24 x3+ 21 x2−12 x
Combining the like terms, we have
¿−x5+2 x4 +3 x4 +24 x3 +4 x2 + 4 x2+ 21 x2−6 x−12 x+16 +1
¿−x5+5 x4 +24 x3 +29 x2−18 x+17
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 5 of 11
Section B - Student Answer Sheet
Questions
Provide your responses in the boxes below each question
Q1
:
Given that
then find:
2P(x) -Q(x) + 3R(x)
2 marks
Satisfactor
y
response
Yes
☐
No
☐
A:
P ( x ) =8−3 x +2 x2+ x4
Q ( x )=x5−3 x4−4 x2−1
R ( x )=8 x3+ 7 x2−4 x
Then, evaluate,
2 P ( x )−Q ( x ) +3 R ( x )
Plugging the values
¿ 2 ( 8−3 x +2 x2+ x4 )− ( x5−3 x4 −4 x2−1 ) +3 (8 x3+7 x2−4 x)
¿ ( 16−6 x+ 4 x2 +2 x4 )− ( x5−3 x4 −4 x2−1 ) +(24 x3 +21 x2 −12 x )
¿ 16−6 x+4 x2+ 2 x4 −x5+ 3 x4 +4 x2+ 1+ 24 x3+ 21 x2−12 x
Combining the like terms, we have
¿−x5+2 x4 +3 x4 +24 x3 +4 x2 + 4 x2+ 21 x2−6 x−12 x+16 +1
¿−x5+5 x4 +24 x3 +29 x2−18 x+17
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 5 of 11

STUDENT
Q2
:
Find the roots of the following polynomial function.
Sketch the graph of this function between
2 marks
Satisfactor
y
response
Yes
☐
No
☐
A: Given polynomial 4 x2 −20 x +9
We can find the roots of the polynomial by using factorization method or using direct formula
Factorization method:
Let the polynomial P ( x )=4 x2−20 x +9
In order to find the root of the polynomial
Set the polynomial equal to zero i.e P ( x )=0
4 x2 −20 x +9=0
Now factorize the left side of the equation
4 x2 −18 x −2 x +9=0
Now,
Take common 2 x from the pair of two terms
2 x ( 2 x−9 ) −1 ( 2 x−9 ) =0
Take ( 2 x−9 ) common from both the terms
( 2 x−9 ) ( 2 x −1 )=0
Therefore, either
( 2 x−9 ) =0∨ ( 2 x−1 )=0 or both will be zero to satisfy the above equation.
Therefore, we have two roots of the polynomial
x= 9
2 ∧x= 1
2
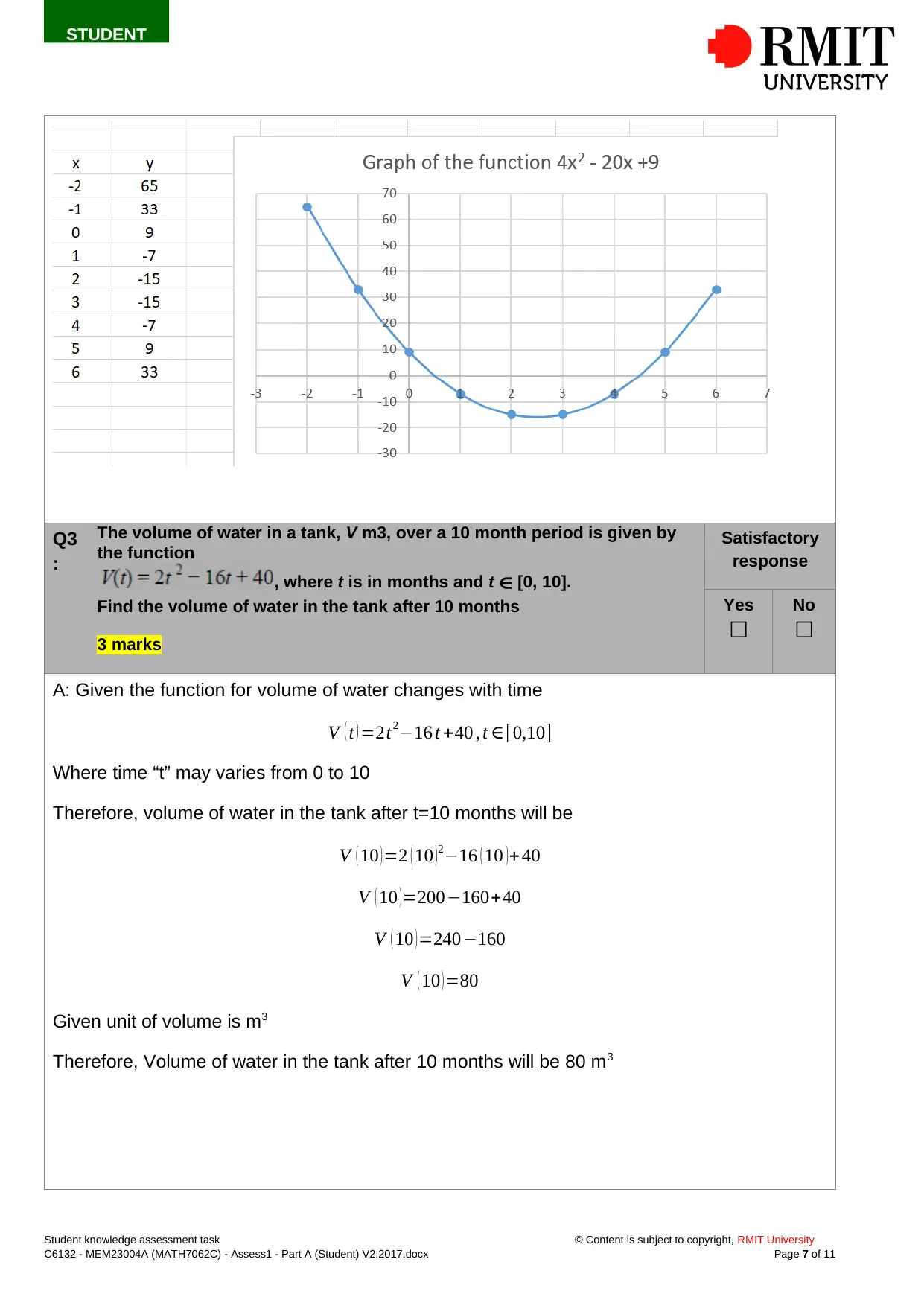
Graph of the function between the interval −2 ≤ x ≤6
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 6 of 11
Q2
:
Find the roots of the following polynomial function.
Sketch the graph of this function between
2 marks
Satisfactor
y
response
Yes
☐
No
☐
A: Given polynomial 4 x2 −20 x +9
We can find the roots of the polynomial by using factorization method or using direct formula
Factorization method:
Let the polynomial P ( x )=4 x2−20 x +9
In order to find the root of the polynomial
Set the polynomial equal to zero i.e P ( x )=0
4 x2 −20 x +9=0
Now factorize the left side of the equation
4 x2 −18 x −2 x +9=0
Now,
Take common 2 x from the pair of two terms
2 x ( 2 x−9 ) −1 ( 2 x−9 ) =0
Take ( 2 x−9 ) common from both the terms
( 2 x−9 ) ( 2 x −1 )=0
Therefore, either
( 2 x−9 ) =0∨ ( 2 x−1 )=0 or both will be zero to satisfy the above equation.
Therefore, we have two roots of the polynomial
x= 9
2 ∧x= 1
2
Graph of the function between the interval −2 ≤ x ≤6
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 6 of 11
STUDENT
Q3
:
The volume of water in a tank, V m3, over a 10 month period is given by
the function
, where t is in months and t ∈ [0, 10].
Find the volume of water in the tank after 10 months
3 marks
Satisfactory
response
Yes
☐
No
☐
A: Given the function for volume of water changes with time
V ( t ) =2t2−16 t +40 , t ∈[0,10]
Where time “t” may varies from 0 to 10
Therefore, volume of water in the tank after t=10 months will be
V ( 10 )=2 ( 10 )2−16 ( 10 )+40
V ( 10 )=200−160+40
V ( 10 )=240−160
V ( 10 )=80
Given unit of volume is m3
Therefore, Volume of water in the tank after 10 months will be 80 m3
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 7 of 11
Q3
:
The volume of water in a tank, V m3, over a 10 month period is given by
the function
, where t is in months and t ∈ [0, 10].
Find the volume of water in the tank after 10 months
3 marks
Satisfactory
response
Yes
☐
No
☐
A: Given the function for volume of water changes with time
V ( t ) =2t2−16 t +40 , t ∈[0,10]
Where time “t” may varies from 0 to 10
Therefore, volume of water in the tank after t=10 months will be
V ( 10 )=2 ( 10 )2−16 ( 10 )+40
V ( 10 )=200−160+40
V ( 10 )=240−160
V ( 10 )=80
Given unit of volume is m3
Therefore, Volume of water in the tank after 10 months will be 80 m3
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 7 of 11
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

STUDENT
Q4
:
Exponential and Logarithm:
Determine the following:
2 marks
Satisfactory
response
Yes
☐
No
☐
A:Given , g ( x ) = 7
4 ex+1
g (−2 )= 7
4 e−2 +1
g ( −2 ) = 7
4 e−1
In decimal form g ( −2 ) =0.6437
g ( √3 )= 7
4 e √3+1
g ( √ 3 ) = 7
4 ( e√ 3 × e1 )
In decimal form g ( √3 )=26.88
g ( 3.6 )= 7
4 e3.6 +1
g ( 3.6 ) = 7
4 e4.6
In decimal form g ( 3.6 )=174.09
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 8 of 11
Q4
:
Exponential and Logarithm:
Determine the following:
2 marks
Satisfactory
response
Yes
☐
No
☐
A:Given , g ( x ) = 7
4 ex+1
g (−2 )= 7
4 e−2 +1
g ( −2 ) = 7
4 e−1
In decimal form g ( −2 ) =0.6437
g ( √3 )= 7
4 e √3+1
g ( √ 3 ) = 7
4 ( e√ 3 × e1 )
In decimal form g ( √3 )=26.88
g ( 3.6 )= 7
4 e3.6 +1
g ( 3.6 ) = 7
4 e4.6
In decimal form g ( 3.6 )=174.09
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 8 of 11
STUDENT
Q5
:
A spectrophotometer measures the concentration of a sample dissolved in
water by shining a light through it and recording the amount of light that
emerges. In other words, if we know the amount of light that is absorbed,
we can calculate the concentration of the sample. For a certain substance
the concentration (in moles per litre) is found by using the formula:
where I0 is the intensity of the incident light and I is the intensity of light
that emerges. Find the
concentration of the substance if the intensity I is 70% of I0.
3 marks
Satisfactory
response
Yes
☐
No
☐
A: Given Relation between concentration of the sample “C”, intensity of the incident light “ I 0”
and intensity of light that emerges “ I”.
C=−2500 × ln ( I
I 0 )
Given, I is 70% of I 0
Therefore, I =0.7 × I 0
Then
C=−2500 × ln ( 0.7 × I0
I 0 )
C=−2500 × ln ( 0.7 )
C=−2500 ×(−0.35667)
C=891.68 moles per litre
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 9 of 11
Q5
:
A spectrophotometer measures the concentration of a sample dissolved in
water by shining a light through it and recording the amount of light that
emerges. In other words, if we know the amount of light that is absorbed,
we can calculate the concentration of the sample. For a certain substance
the concentration (in moles per litre) is found by using the formula:
where I0 is the intensity of the incident light and I is the intensity of light
that emerges. Find the
concentration of the substance if the intensity I is 70% of I0.
3 marks
Satisfactory
response
Yes
☐
No
☐
A: Given Relation between concentration of the sample “C”, intensity of the incident light “ I 0”
and intensity of light that emerges “ I”.
C=−2500 × ln ( I
I 0 )
Given, I is 70% of I 0
Therefore, I =0.7 × I 0
Then
C=−2500 × ln ( 0.7 × I0
I 0 )
C=−2500 × ln ( 0.7 )
C=−2500 ×(−0.35667)
C=891.68 moles per litre
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 9 of 11

STUDENT
Q6
:
The rate at which a battery charges is slower the closer the battery is to its
maximum charge C0. The
time (in hours) required to charge a fully discharged battery to a charge C is
given by:
where k is a positive constant that depends on the battery. For a certain
battery, k = 0.25. If this battery is fully discharged, how long will it take to
charge to 90% of its maximum charge C0?
3 marks
Satisfactor
y
response
Yes
☐
No
☐
A: Given maximum = C0
Positive constant, k = 0.25
Charge required, C = 90% of maximum charge C0
C=0.9 C0
Therefore
According to time and charge required relationship,
t=−k × ln (1− C
C0 )
Plugging all the given values, we have
t=−0.25 × ln (1− 0.9 ×C0
C0 )
t=−0.25 × ln ( 1−0.9 )
t=−0.25 × ln ( 0.1 )
t=−0.25 ×(−2.30)
Therefore, time required to charge 90% of the maximum charge will be
t=0.575 hours
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 10 of 11
Q6
:
The rate at which a battery charges is slower the closer the battery is to its
maximum charge C0. The
time (in hours) required to charge a fully discharged battery to a charge C is
given by:
where k is a positive constant that depends on the battery. For a certain
battery, k = 0.25. If this battery is fully discharged, how long will it take to
charge to 90% of its maximum charge C0?
3 marks
Satisfactor
y
response
Yes
☐
No
☐
A: Given maximum = C0
Positive constant, k = 0.25
Charge required, C = 90% of maximum charge C0
C=0.9 C0
Therefore
According to time and charge required relationship,
t=−k × ln (1− C
C0 )
Plugging all the given values, we have
t=−0.25 × ln (1− 0.9 ×C0
C0 )
t=−0.25 × ln ( 1−0.9 )
t=−0.25 × ln ( 0.1 )
t=−0.25 ×(−2.30)
Therefore, time required to charge 90% of the maximum charge will be
t=0.575 hours
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 10 of 11
Secure Best Marks with AI Grader
Need help grading? Try our AI Grader for instant feedback on your assignments.

STUDENT
Section C - Feedback to Student
Has the candidate successfully completed this assessment task?
Yes No
☐ ☐
Feedback to the candidate
Assessor Name Date
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 11 of 11
Section C - Feedback to Student
Has the candidate successfully completed this assessment task?
Yes No
☐ ☐
Feedback to the candidate
Assessor Name Date
Student knowledge assessment task © Content is subject to copyright, RMIT University
C6132 - MEM23004A (MATH7062C) - Assess1 - Part A (Student) V2.2017.docx Page 11 of 11
1 out of 11
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
© 2024 | Zucol Services PVT LTD | All rights reserved.





