Economics Statistics: Descriptive Analysis, Graphical Representation, Regression

This report provides a descriptive statistical analysis of the relationship between variables in economics statistics. It includes graphical representation and regression analysis to determine the association between the mean values of selling price of a house with other variables. The report concludes that there is a strong relationship between the age, number of rooms, bathrooms, and price of a house.

Economics statistics

TABLE OF CONTENTS
INTRODUCTION......................................................................................................................3
MAIN BODY.............................................................................................................................3
1. Descriptive statistic............................................................................................................3
2. Graphical representation....................................................................................................4
3. Statistical difference between number of room and new and old room.............................4
4. Regression..........................................................................................................................5
5. Regression..........................................................................................................................6
CONCLUSION..........................................................................................................................7
REFERENCES...........................................................................................................................8
INTRODUCTION
Statistic for economics is all about collecting, processing and analysing the economic
data. The present study will helps to determine the relation between variables by applying
different statistical analysis tools. The study will depend upon House price on Aula which
contain the information of 321 houses which sold recently. For that, the report will provide
descriptive statistic and identify the relationship between dependent and independent
variables.
MAIN BODY
1. Descriptive statistic
price rooms baths age
Mean
961006.60
44
3.5856
7
2.3395
64
18.009
35
Standard
Error
24125.132
88 0.0503
0.0430
07
1.8176
48
Median 859000 4 2 4
Mode 1200000 4 3 0
Standard
Deviation
432237.28
87
0.9012
04
0.7705
26
32.565
85
Sample
Variance
1.86829E+
11
0.8121
69
0.5937
11
1060.5
34

Kurtosis
1.8366164
24
1.4822
08
-
0.8730
7
10.774
79
Skewness
1.1443690
02
0.1154
76
-
0.5025
3
3.0601
32
Range 2740000 6 3 189
Minimum 260000 1 1 0
Maximum 3000000 7 4 189
Sum 308483120 1151 751 5781
Count 321 321 321 321
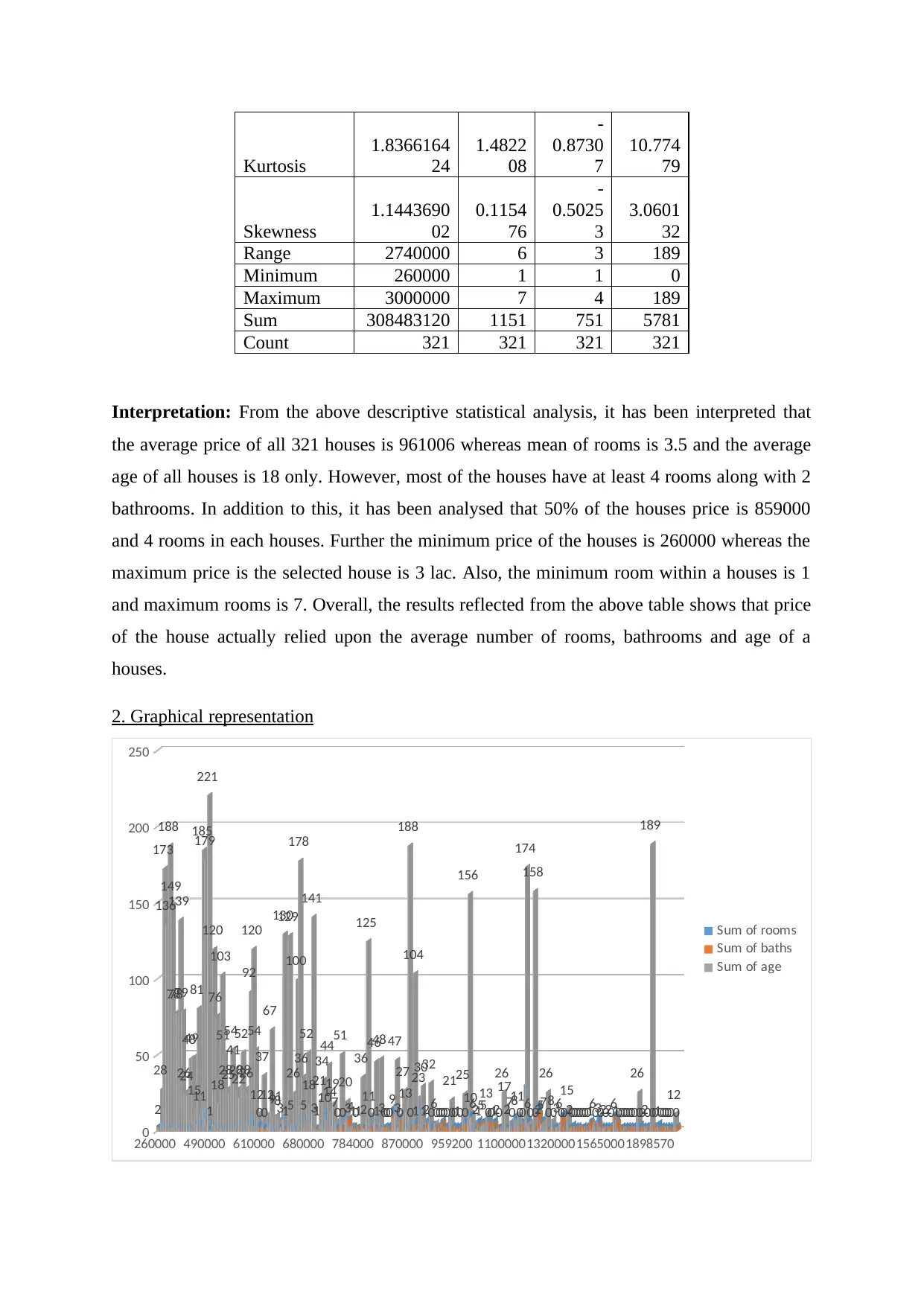
Interpretation: From the above descriptive statistical analysis, it has been interpreted that
the average price of all 321 houses is 961006 whereas mean of rooms is 3.5 and the average
age of all houses is 18 only. However, most of the houses have at least 4 rooms along with 2
bathrooms. In addition to this, it has been analysed that 50% of the houses price is 859000
and 4 rooms in each houses. Further the minimum price of the houses is 260000 whereas the
maximum price is the selected house is 3 lac. Also, the minimum room within a houses is 1
and maximum rooms is 7. Overall, the results reflected from the above table shows that price
of the house actually relied upon the average number of rooms, bathrooms and age of a
houses.
2. Graphical representation
260000 490000 610000 680000 784000 870000 959200 1100000132000015650001898570
0
50
100
150
200
250
2
28
173
136
188
149
7878
139
79
2624
4849
15
81
11
185
179
221
1
120
76
18
103
51
2825
54
41
28
22
52
2826
92
120
54
12
0
37
0
12
67
9118
3
130
1
129
5
26
100
178
36
5
52
18
141
31
21
34
10
44
14
19
7
0
51
0
20
34101
36
2
125
11
0
46
1
48
3000
9
47
30
27
13
188
0
104
1
23
30
12
32
0
6
00000
21
0010
25
0
156
1062155
13
00120
26
17
2
7
0
811
00
174
6
0
158
0257
26
0
8
036
00
15
200000001
6
0302020
6
10000000
26
0020
189
00100000
12
0
Sum of rooms
Sum of baths
Sum of age

Summary: The graphical representation shows that price of the houses is fluctuated with the
number of rooms, bathroom and age. Such that the price will be higher, if number of rooms
will be more than 5 and bathrooms. However, it has been reflected that through the
presentation that there a continuous trend identified from the house data due to variation in
number of rooms and age.
3. Statistical difference between number of room and new and old room
Null hypothesis (H0): There is no statistical difference between the mean values of average
number of rooms and age.
Alternative hypothesis (H1): There is a statistical difference between the mean values of
average number of rooms and age
T test
rooms age
Mean 3.58567
18.0093457
9
Variance
0.81216
9
1060.53428
7
Observations 321 321
Pearson Correlation
-
0.05119
Hypothesized Mean
Difference 0
df 320
t Stat
-
7.92111
P(T<=t) one-tail
1.96E-
14
t Critical one-tail
1.64962
9
P(T<=t) two-tail
3.92E-
14
t Critical two-tail
1.96740
5
Interpretation: In this, the house whose age is less than 50 are define as new,
whereas houses whose age group is more than 50 are fall under the category of old.
Therefore, by applying t-test, it has been interpreted that there is a statistical difference
between the mean values of old and new because the value of p (0.00) is lower than 0.05 and
that is why, alternative hypothesis is accepted over other. So, it can be stated that the average

of rooms is 4 and the age is 18 and that is why, there is a change in the value of rooms when
age of houses is changes frequently.
4. Regression
H0: There is no relationship between average prices of houses with one bathroom.
H1: There is a relationship between average prices of houses with one bathroom.
SUMMARY
OUTPUT
Regression Statistics
Multiple R
0.6259
36
R Square
0.3917
95
Adjusted R
Square
0.3898
89
Standard
Error
33761
8.9
Observatio
ns 321
ANOVA
df SS MS F
Signific
ance F
Regression 1
2.34E+1
3
2.34E
+13
205.4
946
2.55286
E-36
Residual 319
3.64E+1
3
1.14E
+11
Total 320
5.98E+1
3
Coeffi
cients
Standard
Error t Stat
P-
value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept
13952
2.4 60324.62
2.312
859
0.021
366
20837.9
9326
25820
6.8
20837.9
9
258206.
8
baths
35112
7.1 24494.25
14.33
508
2.55
E-36
302936.
3964
39931
7.8
302936.
4
399317.
8
Interpretation: Through the anova output table, it can be stated that there is a significant
difference between the average prices of houses with bathrooms. It is so because the p (0.00 <

0.05) and as a result, it can be stated that null hypothesis is rejected over others.
Papageorgiou and et.al., (2020) also shows that if the number of bathrooms in the house will
increase, it changes the price of houses and vice versa. Thus, it can be stated through
summary output table that there is 62% relationship identified between the variables.
5. Regression
H0: There is no association between the mean values of selling price of house with other
variables
H1: There is an association between the mean values of selling price of house with other
variables
SUMMARY
OUTPUT
Regression Statistics
Multiple R
0.6460
81
R Square
0.4174
21
Adjusted R
Square
0.4119
08
Standard
Error
33147
0.6
Observatio
ns 321
ANOVA
df SS MS F
Signific
ance F
Regression 3 2.5E+13
8.32E
+12
75.71
078
5.95E-
37
Residual 317
3.48E+1
3
1.1E+
11
Total 320
5.98E+1
3
Coeffi
cients
Standard
Error t Stat
P-
value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept
11501
2.6 80493.38
1.428
845
0.154
033 -43356.2
27338
1.3
-
43356.2
273381.
3
rooms
67938.
54 26444.71
2.569
079
0.010
654
15909.2
2
11996
7.9
15909.2
2
119967.
9
baths 27291 33067.11 8.253 4.2E- 207851. 33796 207851. 337969.

0.5 231 15 8 9.2 8 2
age
-
2004.6
6 624.5074
-
3.209
99
0.001
463 -3233.37
-
775.96
1
-
3233.37
-
775.961
Interpretation: The summary output table entails that there is a moderate (64%) relationship
identified between prices of houses with other variables. However, if number of bathroom
and age of houses will chances, there will be 41% changes in the price of houses. Also,
through anova table it can be stated that there is an association between the price of a houses
and other variables such that due to change in rooms of a house price definitely affected.
Therefore, it has been also emphasized by Rahman and et.al., (2021) that there are many
explanatory variables in which price of a house depend and that is why, it shows a positive
relationship between each other.
CONCLUSION
By summing up above it has been concluded that there is a strong relationship
between the age, number of rooms, bathrooms and price of a house as examined through
regression analysis. Moreover, it has been also concluded through the report that average
price of the houses will be 961006 and that is why, the price will fluctuate as per the changes
in other variable.

REFERENCES
Books and Journals
Papageorgiou, G. and et.al., 2020. Investigating factors affecting holiday home purchases in
Greece. Property Management.
Rahman, M. M. and et.al., 2021. Effects of Transportation Accessibility on Residential
Housing Rent: Evidence from Metropolitan City of Khulna, Bangladesh. Journal of
Urban Planning and Development. 147(2). p.04021009.