Forecasting Time Series Assignment 2022

Running head: FORECASTING TIME SERIES 1
Forecasting Times series
Name
Institution

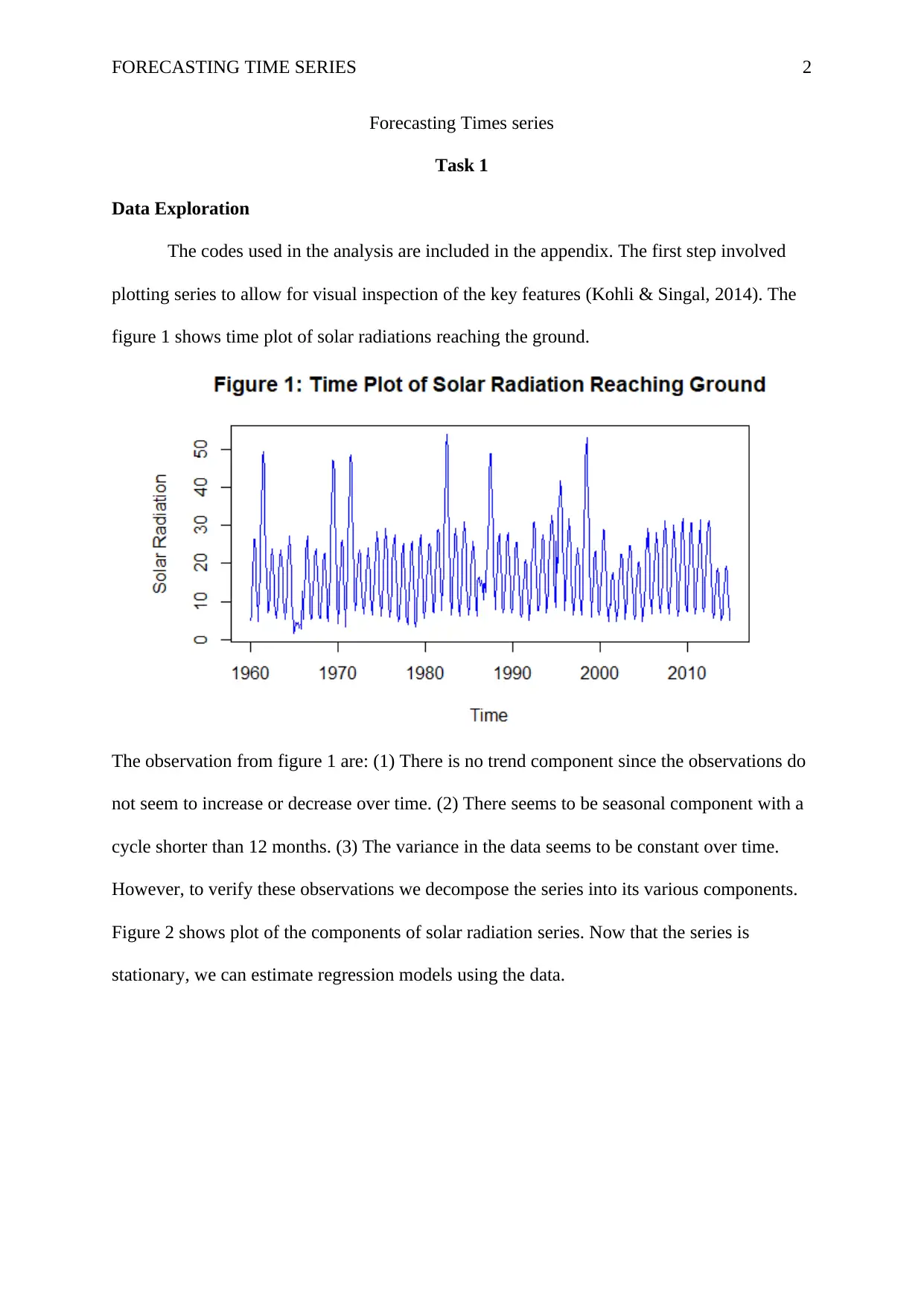
FORECASTING TIME SERIES 2
Forecasting Times series
Task 1
Data Exploration
The codes used in the analysis are included in the appendix. The first step involved
plotting series to allow for visual inspection of the key features (Kohli & Singal, 2014). The
figure 1 shows time plot of solar radiations reaching the ground.
The observation from figure 1 are: (1) There is no trend component since the observations do
not seem to increase or decrease over time. (2) There seems to be seasonal component with a
cycle shorter than 12 months. (3) The variance in the data seems to be constant over time.
However, to verify these observations we decompose the series into its various components.
Figure 2 shows plot of the components of solar radiation series. Now that the series is
stationary, we can estimate regression models using the data.

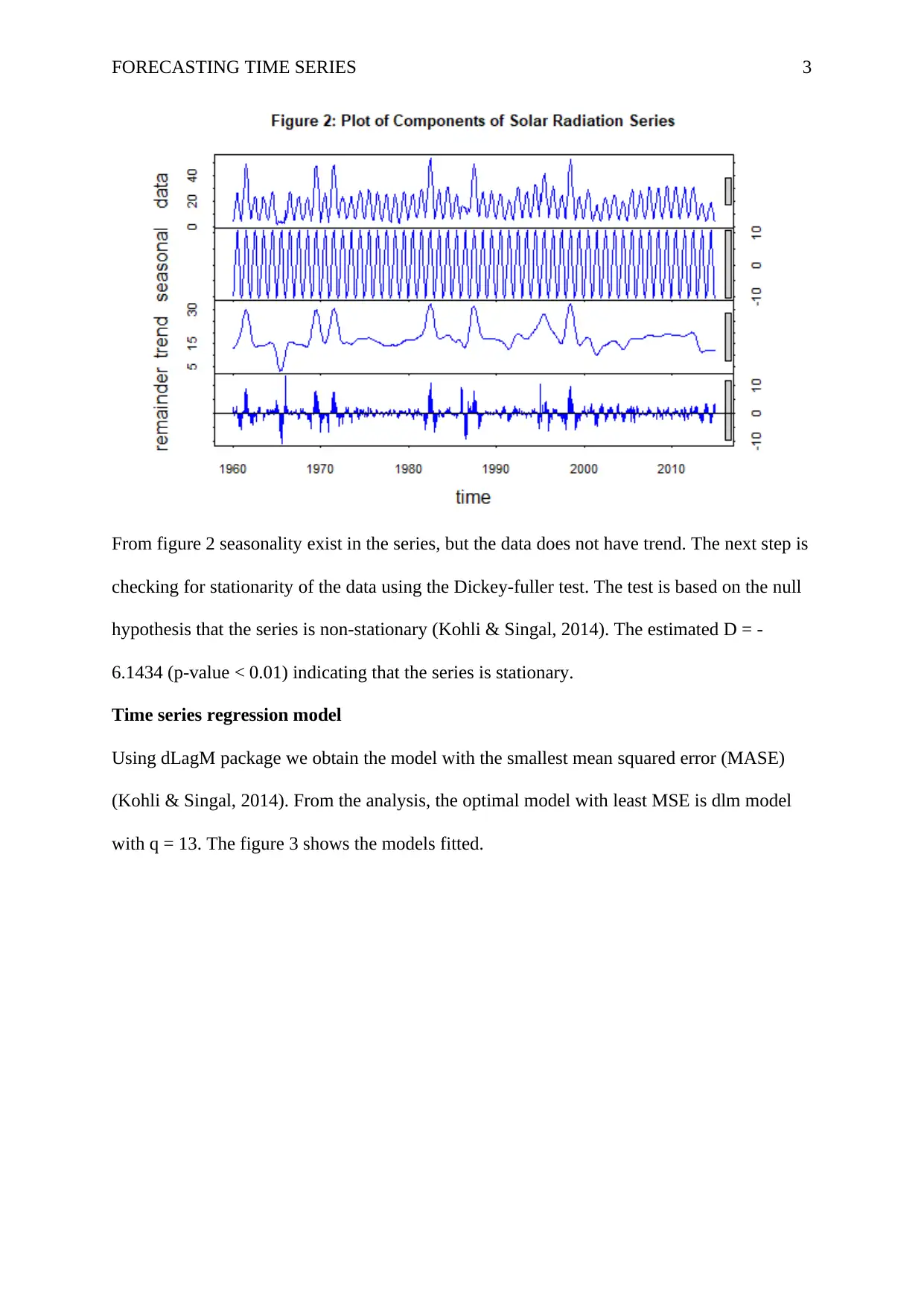
FORECASTING TIME SERIES 3
From figure 2 seasonality exist in the series, but the data does not have trend. The next step is
checking for stationarity of the data using the Dickey-fuller test. The test is based on the null
hypothesis that the series is non-stationary (Kohli & Singal, 2014). The estimated D = -
6.1434 (p-value < 0.01) indicating that the series is stationary.
Time series regression model
Using dLagM package we obtain the model with the smallest mean squared error (MASE)
(Kohli & Singal, 2014). From the analysis, the optimal model with least MSE is dlm model
with q = 13. The figure 3 shows the models fitted.

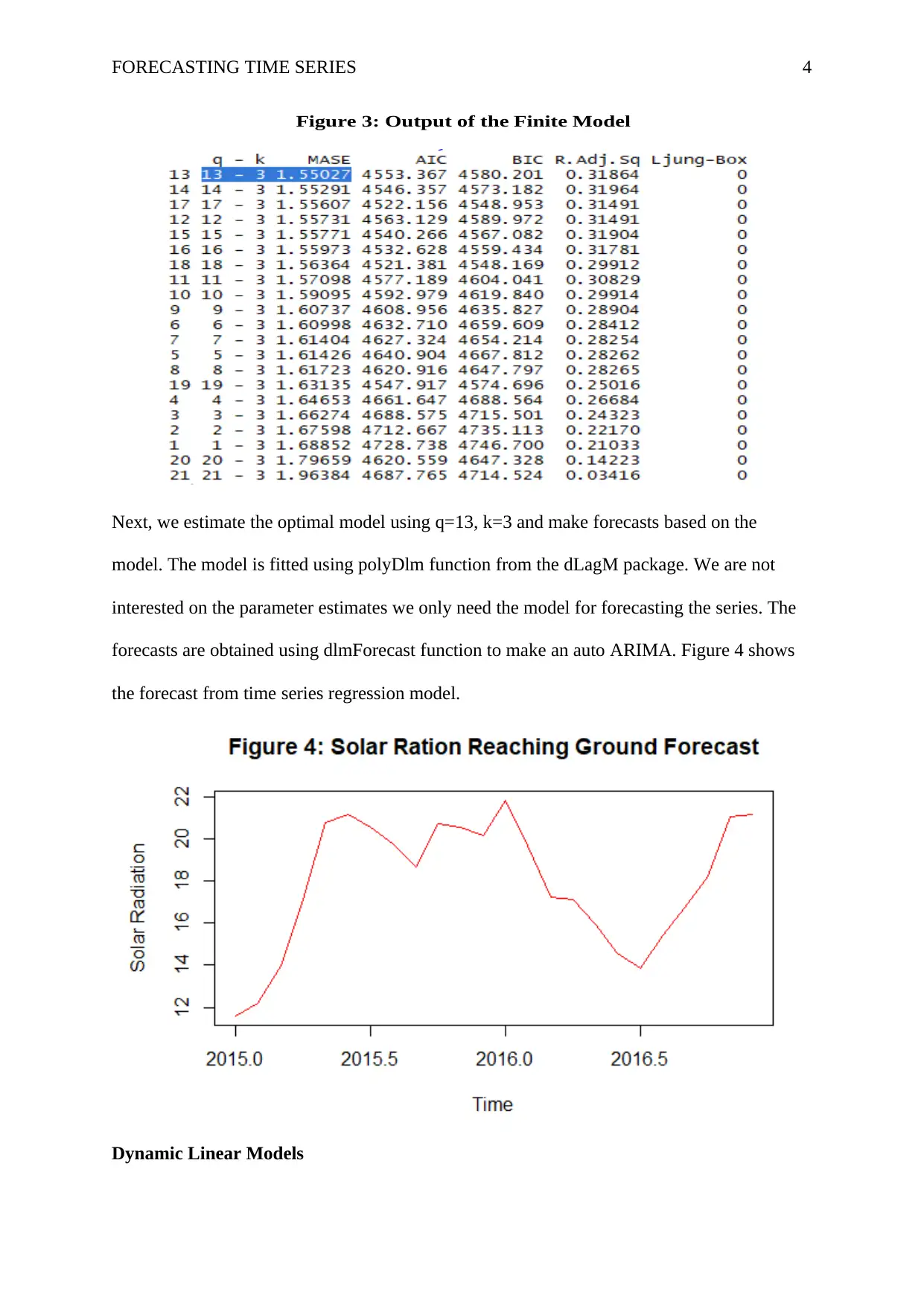
FORECASTING TIME SERIES 4
Figure 3: Output of the Finite Model
Next, we estimate the optimal model using q=13, k=3 and make forecasts based on the
model. The model is fitted using polyDlm function from the dLagM package. We are not
interested on the parameter estimates we only need the model for forecasting the series. The
forecasts are obtained using dlmForecast function to make an auto ARIMA. Figure 4 shows
the forecast from time series regression model.
Dynamic Linear Models

FORECASTING TIME SERIES 5
We use dynlm function to fit a dynamic linear model modelling for trend and seasonality.
The estimates of the model are as follows:
Time series regression with "ts" data:
Start = 1960(1), End = 2014(12)
Call:
dynlm(formula = solar ~ trend(solar) + season(solar))
Residuals:
Min 1Q Median 3Q Max
-25.4345 -2.8904 -0.9763 1.4822 25.3861
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.95437 0.95347 8.343 4.39e-16 ***
trend(solar) 0.00220 0.01555 0.141 0.8876
season(solar)Feb 2.57631 1.20966 2.130 0.0336 *
season(solar)Mar 7.93841 1.20966 6.562 1.09e-10 ***
season(solar)Apr 11.84094 1.20967 9.789 < 2e-16 ***
season(solar)May 16.84047 1.20967 13.922 < 2e-16 ***
season(solar)Jun 19.71994 1.20968 16.302 < 2e-16 ***
season(solar)Jul 20.66586 1.20969 17.084 < 2e-16 ***
season(solar)Aug 17.75799 1.20970 14.680 < 2e-16 ***
season(solar)Sep 12.50653 1.20971 10.338 < 2e-16 ***
season(solar)Oct 6.49828 1.20972 5.372 1.09e-07 ***
season(solar)Nov 1.61139 1.20973 1.332 0.1833
season(solar)Dec -0.68073 1.20975 -0.563 0.5738
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6.344 on 647 degrees of freedom
Multiple R-squared: 0.5897, Adjusted R-squared: 0.5821
F-statistic: 77.49 on 12 and 647 DF, p-value: < 2.2e-16
The overall model is significant since the F-statistics = 77.49 (p-value < 0.000) implying we
can use the model for prediction. The next step is to use the forecast function to predict the
two years ahead solar radiation. Figure 5 shows the plot of the forecasts.

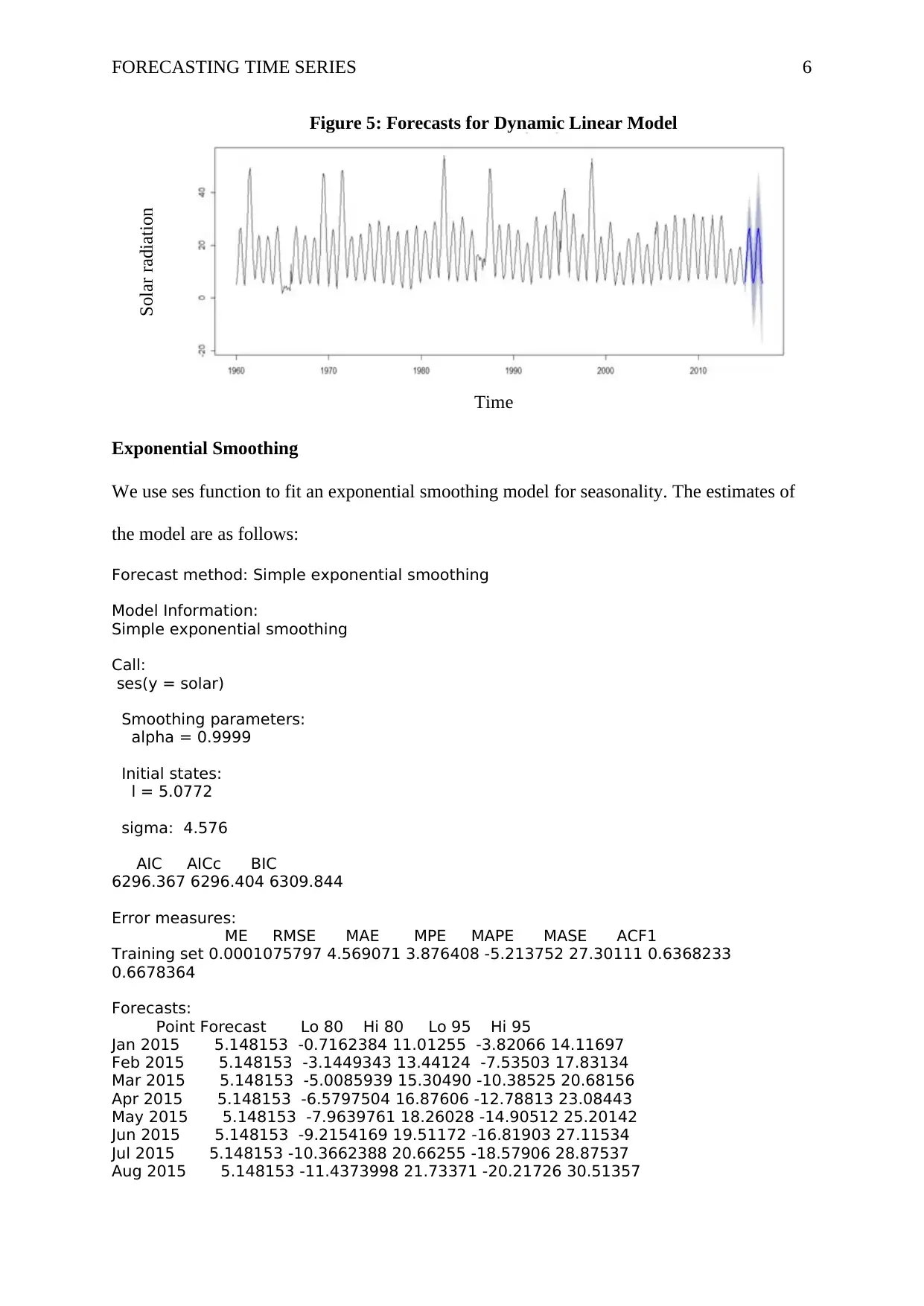
FORECASTING TIME SERIES 6
Solar radiation
Figure 5: Forecasts for Dynamic Linear Model
Time
Exponential Smoothing
We use ses function to fit an exponential smoothing model for seasonality. The estimates of
the model are as follows:
Forecast method: Simple exponential smoothing
Model Information:
Simple exponential smoothing
Call:
ses(y = solar)
Smoothing parameters:
alpha = 0.9999
Initial states:
l = 5.0772
sigma: 4.576
AIC AICc BIC
6296.367 6296.404 6309.844
Error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set 0.0001075797 4.569071 3.876408 -5.213752 27.30111 0.6368233
0.6678364
Forecasts:
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 2015 5.148153 -0.7162384 11.01255 -3.82066 14.11697
Feb 2015 5.148153 -3.1449343 13.44124 -7.53503 17.83134
Mar 2015 5.148153 -5.0085939 15.30490 -10.38525 20.68156
Apr 2015 5.148153 -6.5797504 16.87606 -12.78813 23.08443
May 2015 5.148153 -7.9639761 18.26028 -14.90512 25.20142
Jun 2015 5.148153 -9.2154169 19.51172 -16.81903 27.11534
Jul 2015 5.148153 -10.3662388 20.66255 -18.57906 28.87537
Aug 2015 5.148153 -11.4373998 21.73371 -20.21726 30.51357

FORECASTING TIME SERIES 7
Sep 2015 5.148153 -12.4434579 22.73976 -21.75589 32.05220
Oct 2015 5.148153 -13.3950125 23.69132 -23.21117 33.50748
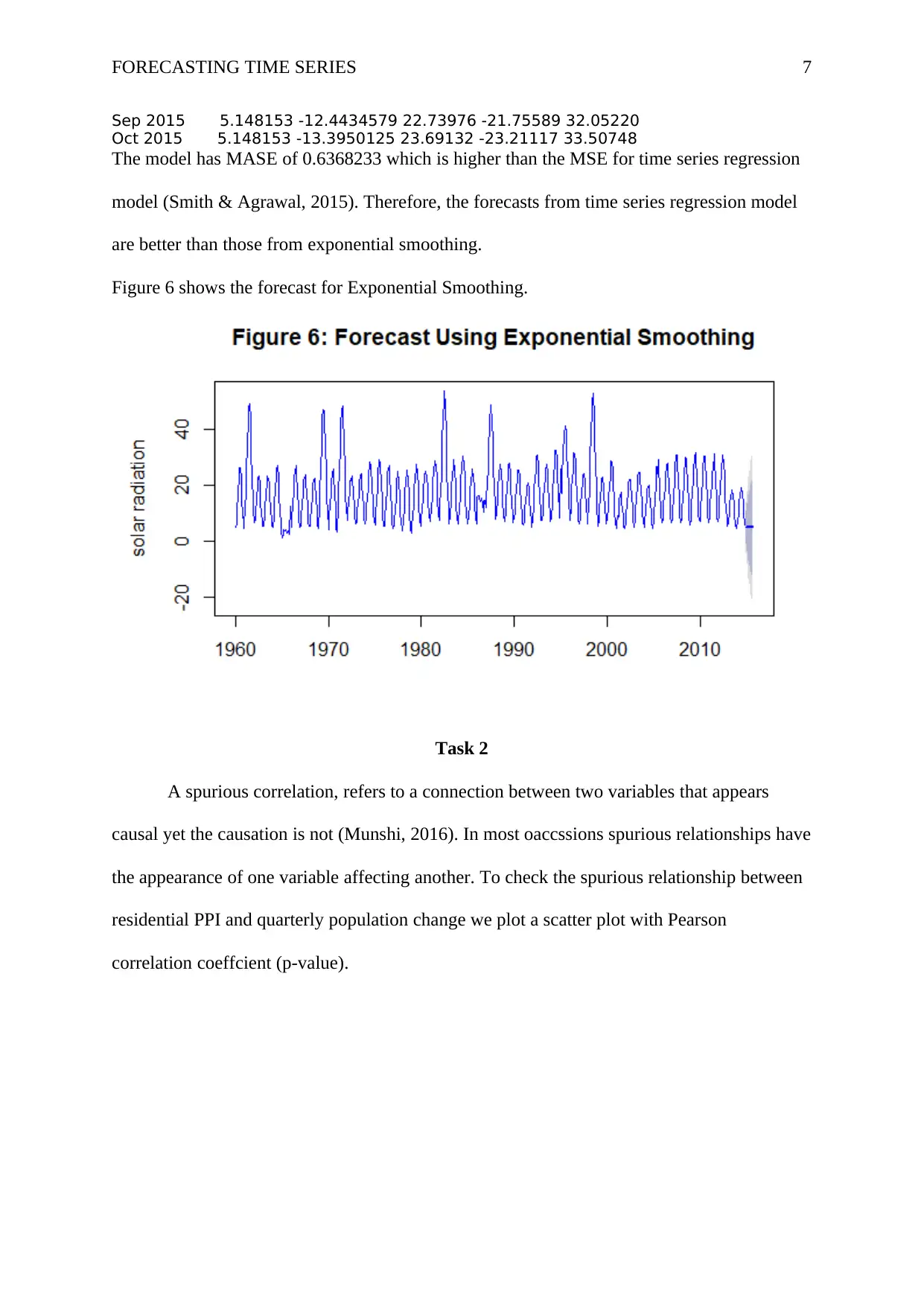
The model has MASE of 0.6368233 which is higher than the MSE for time series regression
model (Smith & Agrawal, 2015). Therefore, the forecasts from time series regression model
are better than those from exponential smoothing.
Figure 6 shows the forecast for Exponential Smoothing.
Task 2
A spurious correlation, refers to a connection between two variables that appears
causal yet the causation is not (Munshi, 2016). In most oaccssions spurious relationships have
the appearance of one variable affecting another. To check the spurious relationship between
residential PPI and quarterly population change we plot a scatter plot with Pearson
correlation coeffcient (p-value).

FORECASTING TIME SERIES 8
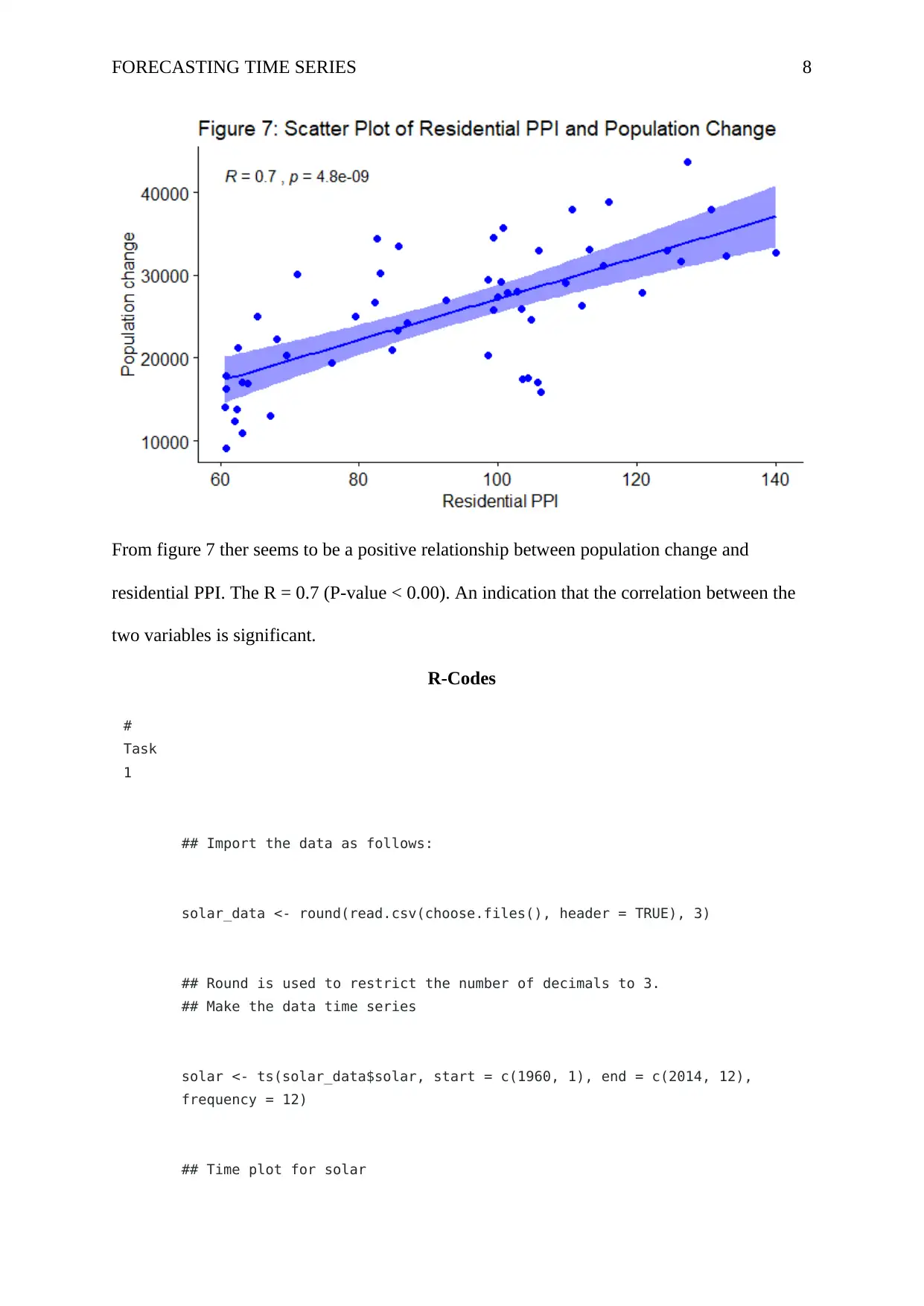
From figure 7 ther seems to be a positive relationship between population change and
residential PPI. The R = 0.7 (P-value < 0.00). An indication that the correlation between the
two variables is significant.
R-Codes
#
Task
1
## Import the data as follows:
solar_data <- round(read.csv(choose.files(), header = TRUE), 3)
## Round is used to restrict the number of decimals to 3.
## Make the data time series
solar <- ts(solar_data$solar, start = c(1960, 1), end = c(2014, 12),
frequency = 12)
## Time plot for solar

FORECASTING TIME SERIES 9
plot(solar, main = "Figure 1: Time Plot of Solar Radiation Reaching
Ground",
ylab = "Solar Radiation", col="blue")
## Decompose the model
library(tseries)
plot(stl(solar, s.window = "periodic"), main = "Figure 2: Plot of
Components of Solar Radiation Series",
col="blue")
## Dickey-Fuller Test
adf.test(solar, alternative = "stationary", k=0)
## Load the libraries required for the analysis
library(dLagM)
## Use finite function to get the model with lowest MSE
finiteDLM <-finiteDLMauto(x=solar_data$ppt, y=solar_data$solar, q.max =
21,
k.order = 3, model.type = "poly", error.type = "MASE",
trace = T)
## Estimate the model
model1 <- polyDlm(x=solar_data$ppt, y=solar_data$solar, q=13, k=3,
show.beta = T)

FORECASTING TIME SERIES 10
## Forecast
data_forecast <- round(read.csv(choose.files(), header = TRUE), 3)
forecast.values <- forecast(model1, data_forecast[,"x"], h=24)
forecast1 <-data.frame(solar=forecast.values$forecasts)
forecast1 <- ts(forecast1$solar, start = c(2015,1), frequency = 12)
plot(forecast1, main="Figure 4: Solar Ration Reaching Ground Forecast",
ylab="Solar Radiation", col="red")
## Remove the package dLagM due to conflict with forecast
detach("package:dLagM", unload=TRUE)
library(dynlm)
## Fit dlm model
model2 <- dynlm(solar~ trend(solar) + season(solar))
forecast2 <-forecast(solar, 24)
plot(forecast2, main = "Figure 5: Forecasts for Dynamic Linear Model",
xlab = "Time", ylab = "Solar Radiation")
# simple exponential – models level
library(forecast)
model3 <- ses(solar)
summary(model3)

FORECASTING TIME SERIES 11
#Plot the forecasted values
plot(model3, main="Figure 6: Forecast Using Exponential Smoothing",
ylab="solar radiation", col="blue")
## Task 2
## Load the data
data2 <- read.csv(choose.files(), header = TRUE)
library("ggpubr")
ggscatter(data2, x = "price", y = "change",
add = "reg.line", conf.int = TRUE,
cor.coef = TRUE, cor.method = "pearson",
xlab = "Residential PPI", ylab = "Population change",color =
"blue",
title = "Figure 7: Scatter Plot of Residential PPI and
Population Change")
References
Kohli, S., & Singal, H. (2014). Data analysis with R. In Proceedings of the 2014 IEEE/ACM
7th International Conference on Utility and Cloud Computing (pp. 537-538). IEEE
Computer Society.
Munshi, J. (2016). Spurious Correlations in Time Series Data: A Note. Available at SSRN
2827927.

FORECASTING TIME SERIES 12
Smith, M., & Agrawal, R. (2015). A Comparison of Time Series Model Forecasting Methods
on Patent Groups. In MAICS (pp. 167-173).