Homework 3: Topics in Graph Theory

This homework covers topics in Graph Theory such as Hall's Theorem, bipartite graphs, Menger's Theorem, and Tutte's Theorem. It includes solutions to problems on matching, stars, and regular graphs. The content is suitable for Mathematics students and includes LaTeX formatting.

Running head: DISCRETE MATHEMATICS
1
Homework 3: Topics in Graph Theory
(Name of Student)
(Institutional Affiliation)
(Date of Submission)
Homework 3

DISCRETE MATHEMATICS 2
Remember to prepare your answers in LaTeX. Refer to hw-template.tex for help in
preparing your HW file. Also, please create an individual page for each solution. Use the
command \pagebreak to force page breaks.
Question One
1. Let G be a bipartite graph with classes A and B and let d ≤ |A| be a fixed positive
integer. Suppose that for every set S A we have⊂
|N(S)| ≥ |S| − d.
Prove that G contains a matching of size |A| − d. [hint: convert G into a graph that
satisfies Hall’s condition.]
Solution.
Let V (G) = A ∪ B be a bipartition of G, with |A| ≥ |B|. Add d new vertices to B, each
connected to all vertices in A. Then let G0 be the new graph. Then G0 has |NG0(S)| ≥ |S|
for every S ⊂ A (S has at least |S| − d neighbors from G, and is connected to the d new
vertices). By Hall’s Theorem, G0 has a matching for A, which has |A| ≥ (|A| + |B|)/2 = |V
(G)|/2 edges. At most d of these edges contain a new vertex of G0, which leaves at least
|V (G)|/2 − d edges from G. Hence G contains a matching of size |A| − d hence proven.

DISCRETE MATHEMATICS 3
Question Two
2. Using the generalized version of Menger’s theorem (see Theorem 2.9) prove
Hall’s theorem.
Solution.
Hall’s theorem, that is, |N(S)| ≥ |S| ∀S ⊂ X.
By letting G be a bipartite graph with vertex classes X and Y. We add two new vertices
a and b to G, and join a to all elements of X, and b to all elements of Y. Let G 0 be the
graph obtained in this way.
Let C be a set of vertices separating a from b in G0. Then N(X \ C) Y ∩ C. Since |C| = |⊆
C ∩ X| + |C ∩ Y |, we have that |C| ≥ |C ∩ X| + |N(X \ C)|. By the condition in Hall’s
theorem, we have that |N(X \ C)| ≥ |X \ C|, so |C| ≥ |C ∩ X| + |X \ C| = |X|.
Thus, by Menger’s theorem, there are |X| independent paths between a and b, this
paths induce a matching in G.

DISCRETE MATHEMATICS 4
Question Three
3. Suppose that instead of Hall’s condition we have the following condition for some
positive integer k:
For every vertex subset S A we have |N(S)| ≥ k|S|.⊆ (1)
Show that G contains a collection of stars on k + 1 vertices that saturate A. A star
on k + 1 is a graph with k vertices of degree 1 all joined to a vertex of degree k.
Let G be a bipartite graph with bipartition (V1, V2) and let M be a maximum matching
of G (Hall’s condition). Then by denoting U the set of M which is unsaturated vertices
in V1, and denoting Z the set of all vertices connected by M-alternating paths to
vertices of U.
Set S=Z V⋂ 1 and T=Z V⋂ 2, then as in the half theorem, we have that every vertex in T
is M- saturated and (s) =T thus G contains a collection of stars on k + 1 vertices thatг
saturate and a star on k + 1 is a graph with k vertices of degree 1 all joined to a vertex
of degree k.

DISCRETE MATHEMATICS 5
Question Four
4. Prove that if G is an n-vertex graph with maximum degree ∆(G) and no vertex of
degree 0, then
.
Solution.
If G is an n-vertex graph with maximum degree ∆ (G) and no vertex of degree 0, then
then the upper bound is immediate and clearly sharp. In order to verify the lower
bound, we employ induction on the size m of a connected graph: if m ≤ 2 then the lower
bound follows.
By assuming that the lower bound holds for all connected graphs of positive sizes not
exceeding k, where k≥2 and letting G be a connected graph of order n having a size k+1.
If G has a cycle edge e, then;
β1(G) ≥ β1(G-e) ≥ n
∆+G , otherwise G is a tree.
If G=K1, n-1, then G contains
If G≠K1, n-1, then G contains an edge e such that (G-e) has two nontrivial components
G1and G2.
By letting ni denote the order of Gi, i=1, 2 and apply the induction hypothesis to G1 and G2
we have;
β1(G) ≥ β1(G1) ≥ β1(G2) ≥ n 1
1+ ∆ G1 +
n 2
1+ ∆ G2
≥ n 1
1+∆ G +
n 2
1+ ∆ G
This implies that β1(G) ≥ β1(G1) ≥ β1(G2) = .

DISCRETE MATHEMATICS 6
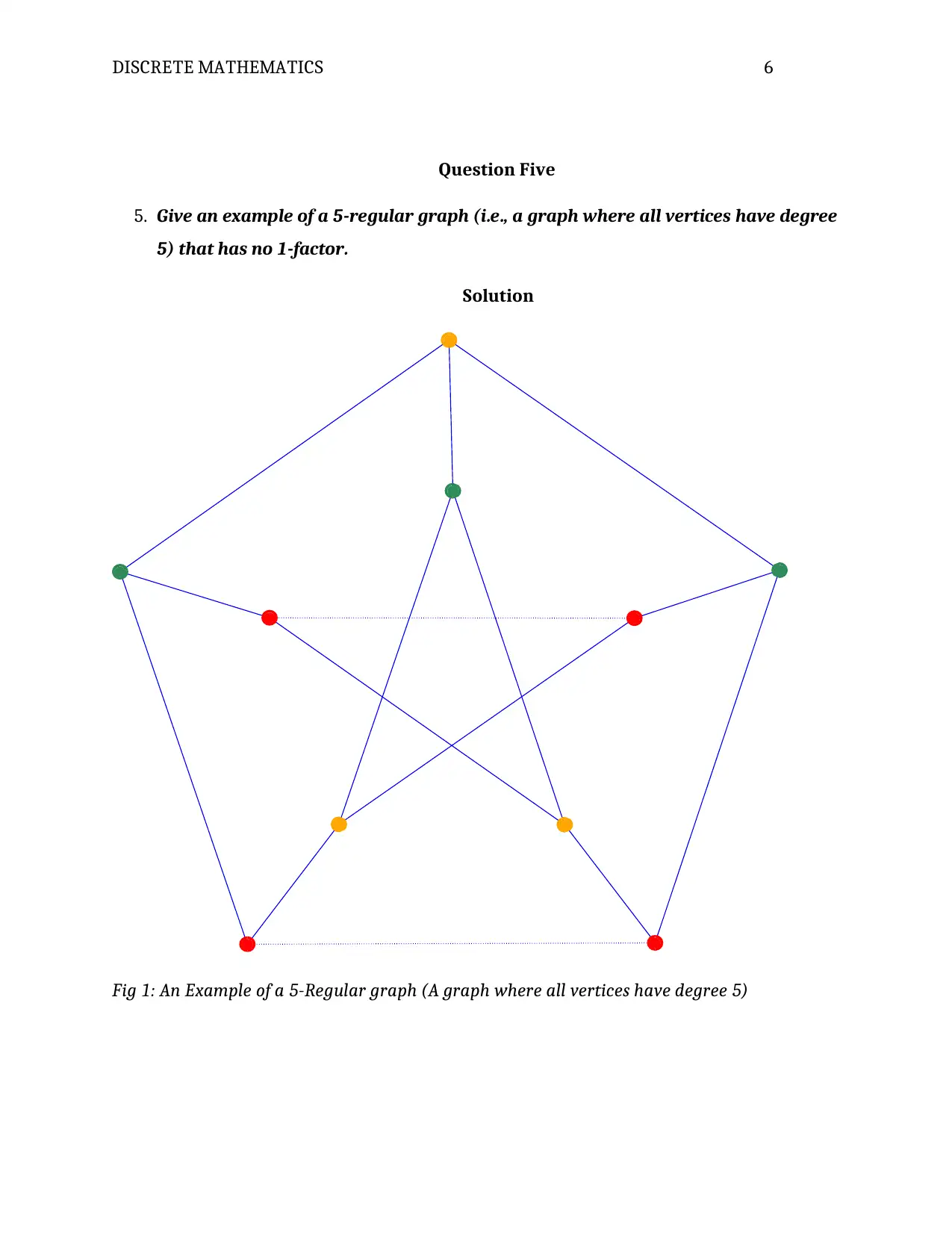
Question Five
5. Give an example of a 5-regular graph (i.e., a graph where all vertices have degree
5) that has no 1-factor.
Solution
Fig 1: An Example of a 5-Regular graph (A graph where all vertices have degree 5)

DISCRETE MATHEMATICS 7

DISCRETE MATHEMATICS 8
Question Six
6. (Graduate exercise) Use Tutte’s theorem to prove Hall’s theorem.
Solution
Hall Theorem: A bipartite graph G with partition (A, B) has a matching of;
A ⇔∀S ⊆ A, ∣N(S) ≥∣ ∣S∣
Tutte’s Theorem: A graph G has a 1-factor o(H \ T) ≤ |T| ∀T ⊂ V (H).
If G has a matching of size |X| and H has a 1-factor (H is graph obtained from G by adding
one vertex to Y if V (G) is odd and then adding the edges of a clique (=a full graph) on the
vertices of Y ) it follows that G satisfies Hall’s condition.
Assuming that H has a 1-factor (i.e. a perfect matching) and let M be the edges in this
matching that are incident with vertices in X. In the construction of the graph H the edges
incident with X did not change so the same set of edges is a matching of size |M| = |X| also in
the original graph G. Conversely if there is a matching M of size |X| in G then this matching
has to touch every vertex in X. Thus the edges of M are still edges in H, matching every
vertex in X to some vertex in Y. There might be some vertices in Y that are not matched by
M, but the construction of H made sure that the graph induced by these vertices is a clique
on an even number of vertices, enabling us to complete the matching.
Also, assuming that G satisfies Hall’s condition for subsets S ⊂ X and let T ⊂ V (H). If Y ⊂
T then there are at most |X| vertices left - each a connected component. But by our
assumption it is clear that |Y | ≥ |X| so that we are okay. Assume therefore that Y 6⊂ T, since
Y forms a clique in H there is one connected component B of H \ T containing all the
vertices Y \ T. Let S = X \ V (B). By construction N(S) ⊂ T so that by assumption |S| ≤ |T|.
The connected components of H \ T are exactly B and the separate vertices of S. If |V (B)| is
even we are therefore done. If not write the vertices of H as a disjoint union V (H) = S tT tV
(B), since the total number of vertices is even either |S| or |T| is even and the other is odd.
In particular we have and we are done again.

DISCRETE MATHEMATICS 9
Now by assuming the condition of Hall’s marriage theorem, namely that |N(S)| ≥ |S| for
every S that is contained either in X or in Y. By the above two paragraphs we have a
matching of size |X| and another matching of size |Y | in the bipartite G. This means that |X|
= |Y | and hence both of these matchings are perfect hence proof.

DISCRETE MATHEMATICS 10
References
D´ıaz, G., & Grammatikopoulos, A., & Kaporis, L., & Kirousis, X., & Perez, D., & Sotiropoulos
(2008). 5-regular graphs are 3-colorable with positive probability. In Algorithms - ESA
2008 (Brodal and Leonardi, eds.), pp. 215–225. LNCS 3669, Springer.
Janson, T., & Luczak, B., & Rucin´ski, A (2011). Random Graphs: Wiley, New York.
Krza¸ka La., & Pagnani B., & Weight. M (2010). Threshold values, stability analysis and
high-q asymptotic for the coloring problem on random graphs, Phys. Rev. E 70, 04678.
M´ezard M., & Zecchina, R (2008). Random K-Satisfiability: From an Analytic Solution to a
new efficient algorithm, Phys. Rev. E 66, 056126.