Design and Finite Element Analysis of Leaf Spring - IJREAT

This paper analyzes the stress, strain and deformation of the current state of virtual prototyping of a Leaf spring which directly improve the quality of product through design aspect. The stress and strain analysis is done to compare with Finite Element Method in order to get the optimum design of the Leaf Spring element for modeling and analysis Solidworks and ANSYS Workbench has been used.

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 50
Design and Finite Element Analysis oDesign and Finite Element Analysis oDesign and Finite Element Analysis oDesign and Finite Element Analysis of Leaf Springf Leaf Springf Leaf Springf Leaf Spring
Pawan Jaiswal 1, Debayan Das 2, Ankit Basnet 3, Saurav Rajgadia 4,
Anush karki 5, Anupam Raj Jha 6, Rakesh Jaiswal 7,
Rabindra Nath Barman 8
1,2,3,4,5,6,7B.Tech students, Department of Mechanical Engineering, NIT Durgapur, Durgapur-713209, India
8Assistant Professor, Department of Mechanical Engineering, NIT Durgapur, Durgapur-713209, India
Abstract
In present era it’s difficult to find Automobile parts builder
with enough money for building and testing real prototypes
of the Automobile parts model, instead they use virtual
prototypes. Leaf Spring has got less attention towards the
stress, strain behaviour. The present study of this paper is to
analyze the stress, strain and deformation of the current
state of virtual prototyping of a Leaf spring which directly
improve the quality of product through design aspect. The
stress and strain analysis is done to compare with Finite
Element Method in order to get the optimum design of the
Leaf Spring element for modeling and analysis Solidworks
and ANSYS Workbench has been used.
Keywords: Solidworks 12.0, ANSYS Workbench, Leaf
Spring, Finite Element Method (FEM).
1. Introduction
Leaf sprigs are crucial suspension elements used on
both light and heavy duty vehicle. It is necessary to
minimize the vertical vibrations impacts and bumps
due to road irregularities and to create a comfortable
ride to the passenger. Leaf springs are widely used
for automobile and rail road suspensions. The leaf
spring should absorb the vertical vibrations and
impacts due to road irregularities by means of
variations in the spring deflection so, that the
potential energy is stored in spring as strain energy
and then released slowly by increasing the energy
storage capabilities of a leaf spring and ensures a
more compliant suspension system.[1-2]
Three dimensional finite element analysis of the leaf
spring consists of a computer model or design that is
stressed and analyzed for specific results. A company
that is able to verify a proposed design will be able to
perform to the clients specifications prior to
manufacturing or construction.[3-6]
The leaf spring is analyzed for stress and strain
acted, deflection using 3D finite element analysis.
The general purpose finite element analysis software
ANSYS is used for present study. The variations of
bending stress, strain and displacement values are
predicted. As the Indian market is becoming one of
the leading companies globally in compare to
multinational companies, a cut throat competition has
a rise between Indian companies and multinational
companies. To struggle in the market globally, it has
become necessary for the Indian industries to
improve and innovate their product. Awachat
industries Limited, Wardha is one of the leading
tractor trolley manufacturers in the region
manufacturing 3000 trolley and above. Now they are
manufacturing them with much economical and
technical consideration. One of the important areas
where one can improve the product quality by
increasing the material quality in the design aspect.
One can design the product in such a way that its

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 51
performance increases as compared to the same
product of other companies.[7]
Fig 1: 3-D Model of Leaf Spring
1.1 Material and its properties
Aluminium alloys are alloys in which aluminium (Al)
is the predominant metal. Aluminium alloys are
widely used in engineering structures and
components where light weight or corrosion
resistance is required. Leaf spring made from
aluminium is light and can absorb high impact at
expense of durability and strength at expense of
affordability.[8]
Aluminium include low density and therefore it
includes low weight, high strength, superior
malleability, easy machining, excellent corrosion
resistance and good thermal and electrical
conductivity which are the most important properties
of aluminum. It is also easy to recycle. Aluminium
alloys commonly have tensile strengths of between
70 -700 MPa. Unlike most steel grades, aluminium
does not become brittle at low temperatures. Instead,
its strength increases. At high temperatures, its
strength decreases. At temperatures continuously
above 100°C, strength is affected to the extent that
the weakening must be taken into consideration.[9]
2. Objective
The objective of problem is to design Leaf spring
made of Aluminium alloy using Solidworks 12.0, and
to carry out the Finite Element Analysis (FEA) on the
prepared model in ANSYS 14.5, and determine the
values of Von Misses equivalent stress, strain and
deflection values.
3. Analytical calculation
The leaf spring behaves like a simply supported beam
and the simply supported beam is subjected to both
bending stress and transverse shear stress. Flexural
rigidity is an important parameter in the leaf spring
design and test out to increase from two ends to the
center.
Stiffness Existing Leaf Spring: Material Aluminium
alloy, bending strength (fb) = 1200Mpa. The stiffness
of the upper and lower springs is calculated by using
the relation given below as:-
K= (f/v) = ((8enbt^3)/(3l^3))
The stiffness = 11537 N/mm, =3455 N/mm.
As the springs are connected in series and there are
two Leaf springs used as isolators in parallel.
3.1 Dynamic Loading
There are different model available for calculating
the load factor. The following spring mass having
one degree of freedom is selected because since the
leaf spring is attached to the trolley is single axle the
Centre of gravity of the trolley lies nears the wheels.
The mass (m ") represents the chassis of the trailer
and the spring constant represents the shock-
isolator. The spring is considered as linear near the
wheels.
"/g =0.64
Where, Vs = shock velocity changes in m/sec
=natural frequency of isolator experienced by
chassis is expressed as dimensionless multiple of the
acceleration due to gravity. The value of is
calculated by:-
=1/2*3.1415 ∗ 1000/M
M=Maximum Load Acting on the System=6000kg
=2.54 cps
To find out Vs vertical downward velocity.
we have, s= ut+

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 52
Where, u= initial downward velocity
S= also Vs = u +gt
We get, Vs= 2
Considering a sudden drop of depth to 0.15 the
various values for different values of the natural
frequencies are calculated. Table 1 shows the
equivalent load capacity.
Table1: Equivalent load capacity
Equivalent static load for static load capacity at
various values of multiple factor " for different
natural frequency. Thus considering the maximum
load capacity of 6000 kg which is the capacity of the
system and a sudden depth of 0.15m the dynamic
load factor is 2.70.thus it means that the trolley leaf
spring should have static strength sufficient to
support 2.70 times their normal static.
3.2 Bending stresses and Deflections of leaf
spring
Bending stress developed:
Considering the maximum load capacity of 6000 kg
which is the capacity of the system and multiplying it
with the dynamic load factor of 2.70 for the
equivalent static capacity. We get the equivalent
static capacity as:
Static load (kg) = 6000 kg
Load factor = 2.70
Equivalent static capacity = static load × load factor
Therefore, equivalent static capacity = 6000×2.70
Therefore F = (16200×9.8)/2 = 79461 N
Now bending moment = 3×F×L/( 2×N×B× )
Where,
F= Maximum static force = 79461 N
L= Length of the leaf spring = 435mm
N= number of leafs= 17
B= width of leaf = 70mm
T=thickness of the leafs= 10mm
= 3×79461×435/ (2×17×70×10 )
= 435.70 N/
Developed stress i.e. bending stress is 435.70 N/
Developed Deflections of Leaf Spring:
δ (developed) = 3×F×!" /(8×E×N×B× " )
Where, F= Maximum static force = 79461 N
L= Length of the leaf spring = 435mm
N= Number of Leafs= 17
B= Width of Leaf = 70mm
T=Thickness of the Leafs= 10mm
E=Modulus of Elasticity for (Al alloy) multiplate
Leaf= 7.1*10#N/
δ = 3×79461×435" / (8 × 2.04×105 × 17 × 70 × 10" )
So, developed deflection = 29.03 mm
Also, permitted stress (permitted) = 1200 N/
(Permitted) = 1100×)*
)* =0.8+2.5/t
= 1.05
= 1200×1.05
=1260 N/
For this permitted value of bending stress the
permitted deflection can be calculated as:
1260= 3×F×435/(2×17×70×100)
F = 229793.1N δ
We get the permitted deflection as:
δ
(permitted)=3×229793.1×435" /(8×7.1*10#×17×70×
10" )
= 83.95 mm
Deflection using the number of graduated Leafs and
number of full length Leafs:
Where, F= Maximum static force = 79461N
L= Length of the leaf spring = 435mm
N= number of leafs= 17
B= width of leaf = 70mm
T=thickness of the leafs= 10mm
Static
load
(kg)
+, - .
" Equivalent static
capacity (kg)
1000 6.20 6.61 6610
2000 4.38 4.69 9380
3000 3.58 3.82 11460
4000 3.10 3.30 13200
5000 2.77 2.95 14750
6000 2.53 2.70 16200

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 53
/ 0=number of full length leaves=1
/ 1 =number of graduated leaves=16
δ= 3×F×!" /8×E×/ 1 ×B×T3 [1/ (1+1.5(/ 0// 1 ))]
δ = 28.20mm
Developed bending stress (developed)
=3×F×L/(2×N×B× )[(1.5/(1+1.5*(/ 0// 1 ))]
=597.53 N/
The values are approximately similar to that of
calculated before without considering the number of
graduated leaves and full length leaves
independently.
As from above δ (developed) ‹ δ (permitted)
Hence, the design is safe.
Also (developed) ‹ (permitted)
Hence, the design is safe.
Also the factor of safety can be calculated as:
F.O.S = (permitted)/ (developed)
= 1260 N/ /435.70 N/
= 2.8
3.3 Specifications of Leaf spring
Table 2: specification of leaf spring
Description Upper Spring
(mm)
Lower Spring
(mm)
Number of leaves
(n) 6 11
Width of leaves
(b) 70 70
Thickness of
leaves (t) 10 10
Effective length 410 750
Young modulus
(e) 7.1*10# N/7.1*10# N/
4. Methodology
For the analysis of Leaf spring we have designed our
model in Solidworks 12.0 and then save it as IGES
format for exporting the part into ANSYS 14.5
Workbench environment.
4.1 Meshing:
The figure 2. Shown is the meshed model of rigid
flange coupling in the ANSYS analysis for the static
structural process. To analyze the FEM, default type
of mesh is used for the Leaf spring in the ANSYS
environment. The number of elements used in this
meshing is 285984 and the number of nodes is
1406340. In this process default type of meshing is
done to analyze the process. Using the working
condition of leaf spring a dynamic loading comes
into picture consequently. The determination of the
stress, strain and deformation over leaf spring is
essential. So, the model is meshed and then analyzed
to get the detail and authentic result of the stress,
strain and deformation at dynamic condition.[10]
Fig 2: Mesh model of Leaf Spring
4.2 Finite element method (FEM)
The Finite element method (FEM) is a numerical
technique for finding the approximate solutions to
boundary value problems for partial differential
equations. It uses subdivision of a whole problem
domain into simpler part, called finite elements and
solve the problem by minimizing an associated error
function. Finite element model is constructed that
simulates boundary condition of the vehicle and test
rig. Boundary conditions of finite elements are
simplified suitably and implemented to the model.
Leaf spring is modeled with rectangular type of
default elements. At the beginning, the leaf spring

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 54
was tried to be simulated within the entire vehicle
Finite Element Model. However, not only the time of
calculation will considerably increase but also the
accuracy of the results will decrease because of the
possible errors in the modeling of high nonlinearities.
Therefore, a simulation method was developed based
on the Finite Element Analysis. Moreover, the stress,
strain and deformation were taken into account
carefully, especially for multi-layer leaf springs. In
this study, the mesh and model were generated with
the software ANSYS and Solidworks
5. Analysis of Leaf spring
Fig 3: Equivalent stress of Leaf Spring
Fig 4: Equivalent elastic strain of Leaf Spring
Fig 5: Strain energy of Leaf Spring
Fig 7: Directional deformation of Leaf Spring
Fig 6: Total Deformation of Leaf Spring

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 55
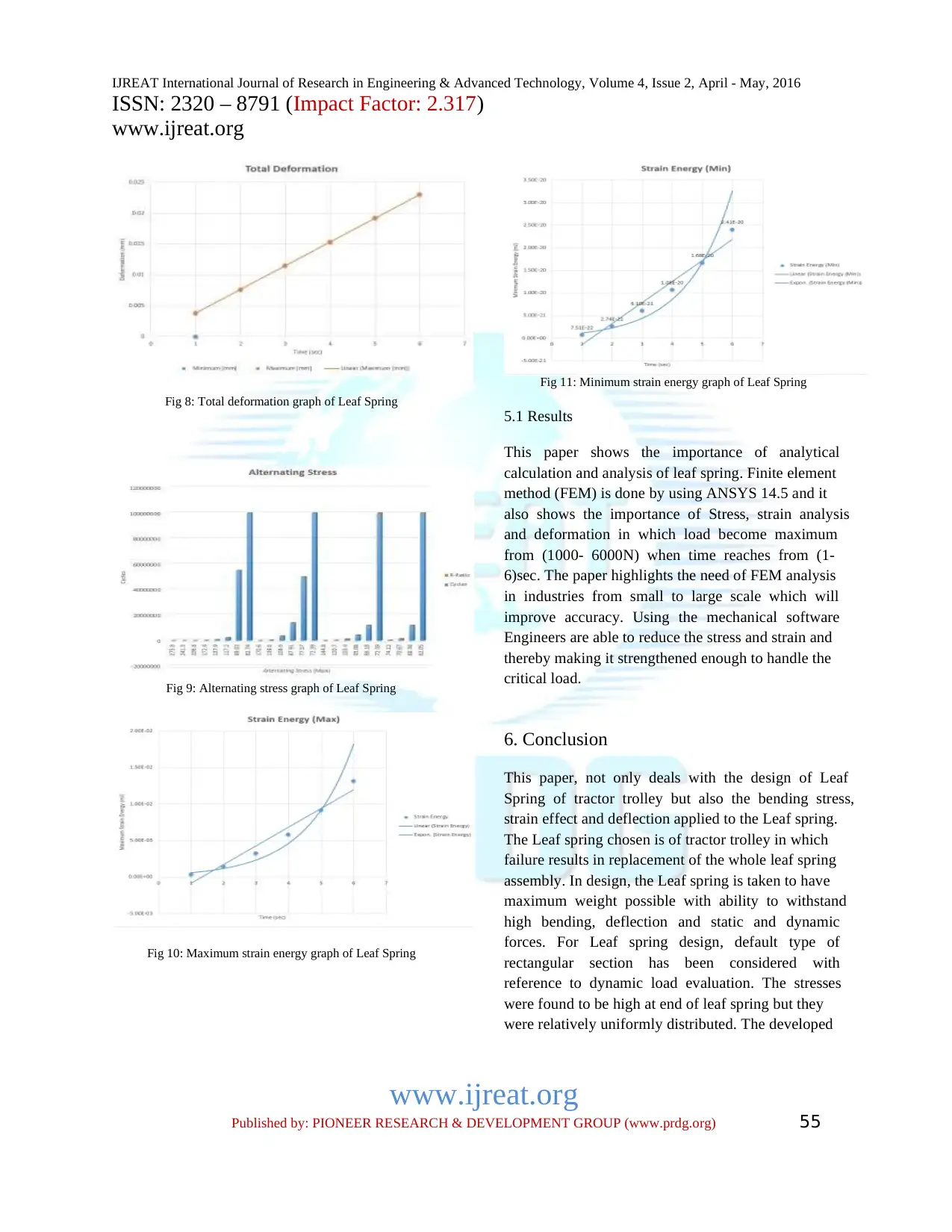
Fig 8: Total deformation graph of Leaf Spring
Fig 9: Alternating stress graph of Leaf Spring
Fig 10: Maximum strain energy graph of Leaf Spring
Fig 11: Minimum strain energy graph of Leaf Spring
5.1 Results
This paper shows the importance of analytical
calculation and analysis of leaf spring. Finite element
method (FEM) is done by using ANSYS 14.5 and it
also shows the importance of Stress, strain analysis
and deformation in which load become maximum
from (1000- 6000N) when time reaches from (1-
6)sec. The paper highlights the need of FEM analysis
in industries from small to large scale which will
improve accuracy. Using the mechanical software
Engineers are able to reduce the stress and strain and
thereby making it strengthened enough to handle the
critical load.
6. Conclusion
This paper, not only deals with the design of Leaf
Spring of tractor trolley but also the bending stress,
strain effect and deflection applied to the Leaf spring.
The Leaf spring chosen is of tractor trolley in which
failure results in replacement of the whole leaf spring
assembly. In design, the Leaf spring is taken to have
maximum weight possible with ability to withstand
high bending, deflection and static and dynamic
forces. For Leaf spring design, default type of
rectangular section has been considered with
reference to dynamic load evaluation. The stresses
were found to be high at end of leaf spring but they
were relatively uniformly distributed. The developed

IJREAT International Journal of Research in Engineering & Advanced Technology, Volume 4, Issue 2, April - May, 2016
ISSN: 2320 – 8791 (Impact Factor: 2.317)
www.ijreat.org
www.ijreat.org
Published by: PIONEER RESEARCH & DEVELOPMENT GROUP (www.prdg.org) 56
stress and deflection values have been found to be
435.70 N/ and 29.03 mm
7. References
[1] V.B. Bhandari, Design of Machine Elements, ISBN: 0-
07-0681791-1, Design of IC Engine Component, Page no.
437-441
[2]https://en.wikipedia.org/wiki/Leaf_spring
[3] Rajendran, I., Vijayarangan, S. “Optimal Design of a
Composite Leaf Spring using Genetic Algorithms Int. Jr.
of Computer
and Structures” 79 2001: pp. 1121 – 1129.
[4] Rajendran, I., Vijayarangan, S. “Design and Analysis of
a Composite Leaf Spring Journal of Institute of Engineers
India” 82, 2002: pp. 180 – 187.
[5] Daugherty, R. L. Composite Leaf Springs in Heavy
Truck Applications. K.Kawata, T.Akasaka (Eds).
Composite
[6] Prof. N.P.Dhoshi, Prof .N.K.Ingole, Prof .U.D.Gulhane
“Analysis and Modification of Leaf Spring of Tractor
Trailer Using Analytical and Finite Element Method”
(IJMER), Vol.1, Issue.2, pp-719-722, ISSN: 2249-6645
[7]https://www.google.co.in/webhp?sourceid=chromeinsta
nt&ion=1&espv=2&ie=UTF8#q=Awachat+industries+Lim
ited
[8] https://en.wikipedia.org/wiki/Aluminium_alloy
[9]http://www.aluminiumdesign.net/whyaluminium/propert
ies-of-aluminium/
[10] Saurav Rajgadia, Debayan Das, Pawan Jaiswal, Ankit
Basnet, Anupam Raj Jha, Rakesh Jaiswal, Anush Karki,
Rabindra Nath Barman “Design and Stress-Analysis of a
Rigid Flange Coupling using FEM” (IJIRSET), vol. 4,
Issue 10, October 2015, IISN :2319-8753
[11] y.s. cong, m.z. omar, l.b. chua, s. abdullah “Fatigue
life prediction of parabolic leaf spring under various road
conditions”(ELSEVIER),www.elsevier.com/locate/engfaila
nal
[12] Mahmut Duruúa*, Levent KÕrkayakb, Aykut
Ceyhana, Kagan Kozana “Fatigue Life Prediction of Z
Type Leaf Spring and New Approach to Verification
Method” Procedia Engineering 101 ( 2015 ) 143 – 150,
www.sciencedirect.com
[13] Debayan Das, Saurav Rajgadia, Anush Karki, Ankit
Basnet, Pawan Jaiswal, Rakesh Jaiswal, Anupam Raj Jha,
Rabindra Nath Barman “Design And Finite Element
Analysis Of Connecting Rod Using Solidworks And
ANSYS Workbench” (IJREAT), Volume 3, Issue 4, Aug-
Sept, 2015, ISSN: 2320 – 8791